7.8 The t-Distribution
In nearly all practical situations the standard deviation of the population that we sample from is unknown and has to be estimated from the data. Relying on the central limit effect we may assume that our sample mean 
is normally distributed and that its standard deviation can be estimated by 
. Then the transformed variable:
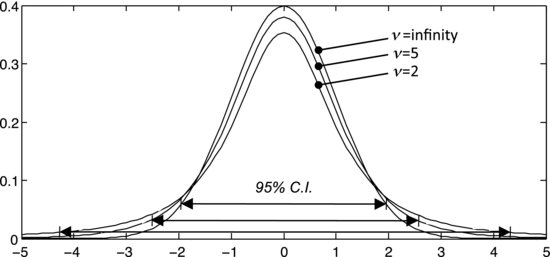
follows a so-called t-distribution. As previously mentioned, a larger sample gives a more reliable estimate of the standard deviation, so you are probably not surprised that the t-distribution depends on the number of degrees of freedom, ν, of the sample. This is illustrated in Figure 7.16, showing t-distributions for ν = 2, 5, and infinity. Note that they become wider and flatter when ν decreases, but the mean is always zero. The t-distribution's standard deviation is:
Figure 7.16 Examples of t-distributions with two, five and infinite degrees of freedom.
(7.14) 
meaning that, as ν becomes large, σ approaches one and the distribution approaches the standard normal distribution. The standard normal distribution is, therefore, a special case of the t-distribution.
Now, let us return to the dietary experiment. We did not know σ and had a sample too small for using the standard normal distribution. Now that we know of the t-distribution, which is suited for small samples, we may use Equation 7.13 and continue our analysis. The confidence interval for μ is simply:
We arrive at this equation exactly as we did with Equation 7.12. (It is a good exercise to do this by working through Box 7.2 using t instead of Z.) Instead of 
we use 
, which must be determined for the desired significance level α, and the appropriate number of degrees of freedom ν, in order to calculate the confidence interval. In our sample, ν = 15 − 1 = 14 and, for a 95% interval, α/2 = 0.025. If you look in the table of probability points for the t-distribution in the Appendix you find that this corresponds to = 2.145.
In our sample, the mean difference in blood pressure is −5.8 mm Hg and the sample standard deviation is 4.7 mm Hg. Putting these values into Equation 7.15 we find that the 95% confidence interval for the mean blood pressure drop extends from −8.4 to −3.2 mm Hg. We may conclude that, at the 95% confidence level, the diet is effective.1
Note that this does not mean that there is 95% probability that the population mean μ lies within this interval. The confidence interval makes a probability statement about the data, not about the population parameter that it estimates. In fact, it makes little sense to make a probability statement about the population mean, since it is not a random variable. The correct interpretation is that, if we were to take repeated samples, the confidence intervals calculated from them would include μ roughly 95% of the time.
The confidence interval is an interval estimate of an unknown parameter. The width of the interval says something about the reliability of the estimate. Looking at Equation 7.15 we see that the reliability increases when the sample size increases and when the variation within our sample decreases.
In this chapter, we have introduced some important concepts that form the basis of more advanced statistical techniques. We have already seen how sample statistics can be used to estimate properties of the parent distribution that the sample came from, such as confidence intervals for the population mean. This type of analysis is called inferential statistics and is introduced further in the next chapter, where it will become clear why knowledge in statistics is useful in the design and analysis of experiments.