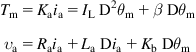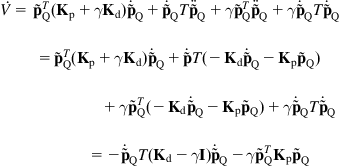Mobile Robot Control I
The Lyapunov-Based Method
This chapter deals with the general problem of determining the forces and torques that must be developed by the robotic actuators in order for the robot to go at a desired position/posture, track a desired trajectory, and, in general, to perform some task with a desired quality of performance. The controllers to be presented in the chapter assume that the goal of the control and the robot dynamic parameters are precisely known, and if this goal (posture or path) is changing, the change is compatible with the environment, and risk free. The particular objectives of the chapter are (i) to provide a minimal set of general control concepts and methods that are used in robot control, (ii) to study the basic general robot controllers that are applicable to all types of robots, and (iii) to present a number of feedback controllers, designed using the Lyapunov-based control theory, for the differential drive, car-like, and omnidirectional mobile robots. These controllers refer to the problems of position (posture) tracking, trajectory tracking, parking, and leader following.
Keywords
Lyapunov stability; DC motor model; state feedback control; computed torque control; kinematic tracking control; dynamic tracking control; polar coordinate-based robot model; parking control; leader–follower control; kinematic controller; dynamic controller; omnidirectional robot control
5.1 Introduction
Robot control deals with the problem of determining the forces and torques that must be developed by the robotic actuators in order for the robot to go at a desired position, track a desired trajectory, and, in general, to perform some task with desired performance requirements. The solution to control problems in robotics (fixed and mobile) is more complicated than usual due to the inertial forces, coupling reaction forces, and gravity effects. The performance requirements concern both the transient period and the steady-state period. In well-structured and fixed environments, such as the factory, the environment can be arranged to match the capabilities of the robot. In these cases, it can be assured that the robot knows certainly the configuration of the environment, and people are protected from the robot’s operation. In such controlled environments, it is sufficient to employ some type of model-based control, but in uncertain and varying (uncontrolled) environments, the control algorithms must be more sophisticated involving some kind of intelligence. The techniques to be presented in this chapter assume that the goal of the control and the robot kinematic and dynamic parameters are precisely known, and if this goal (posture or path) is changing, the change is compatible with the environment, and risk free.
Specifically, the objectives of the chapter are as follows:
• To provide a minimal set of general control concepts and methods that are used in the control of robots
• To study the basic general robot controllers that are applicable to all types of robots
• To present a number of feedback controllers, designed using the Lyapunov-based control theory, for the differential drive, car-like, and omnidirectional mobile robots.
These controllers refer to the problems of position (posture) tracking, trajectory tracking, parking, and leader following. In all cases, the control design involves two stages, viz., kinematic control (where only the kinematic models are used), and dynamic control (where the robot dynamics and actuators are also taken into account).
5.2 Background Concepts
In this section, the following fundamental control concepts and techniques are briefly discussed:
Knowledge of these concepts is a basic prerequisite for the understanding of the material presented in the chapter. Full accounts are given in standard control textbooks [1].
5.2.1 State-Space Model
The state-space model of a control system is based on the concept of state vector 
, which is the minimum dimensionality Euclidean vector, with components called state variables, the knowledge of which at an initial time 
, together with the input vector 
, for 
, determines completely the behavior of the system for any time 
. The dimension 
of the state vector specifies the system’s dimensionality.
The above definition of the state means that the state of the system is determined by its initial value 
at 
and the input for 
, and is independent of the state and the inputs for times previous to 
.
It is noted that the state variables 
of an n-dimensional system may not necessarily be measurable physical quantities, although in practice, an effort is made to use as more as possible measurable variables, because the state feedback control laws need all of them.
The expression of 
as a function of 
, and 
, 
, that is, 
, is called the system’s trajectory.
The output 
of the system is a similar function of 
, 
, and 
, that is:
The trajectories satisfy the transition property:
for all 
, where 
.
In state-space model, the dynamic model of a nonlinear system (in continuous time) has the form:
(5.1a)
(5.1b)
where 
and 
are nonlinear vector functions of their arguments with proper dimensionality and the continuity and smoothness properties required in each case. The state vector 
belongs to the state space 
, the input (control) 
belongs to the input space 
, and the output 
to the output space 
, where 
, 
, 
, and 
is the n-dimensional Euclidean space.
If the vector functions 
and 
are linear, then the system is linear and is described by the model:
(5.2a)
(5.2b)
where 
, 
, 
, 
may be time-invariant or time-varying matrices of proper dimensionality (in many cases, 
). A linear state-space model with the following matrices, 
, 
, and 
(scalar), is called the controllable canonical model of the system that represents:
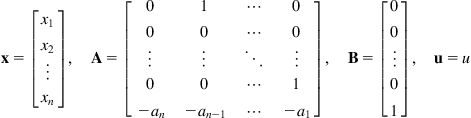(5.3)
For a scalar output 
, a linear time-invariant system described by the nth-order differential equation:
or transfer function:
(5.4)
where 
is the complex frequency variable, can be modeled as in Eqs. (5.2a), (5.2b), and (5.3), if we define the state variables 
as:
(5.5)
Indeed, using Eq. (5.5) we get:
which gives the state-space model ((5.2a), (5.2b), and (5.3)) with:
(5.6)
This model, also called phase variables canonical model, is very convenient for the pole-placement (or assignment) state feedback controller design.
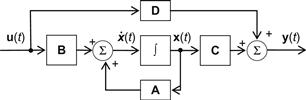
The block diagram representation of the general model (5.2a) and ((5.2b)) has the form shown in Figure 5.1.
Other state-space canonical models of the system (5.2a) and ((5.2b)) are the observable canonical form and the Jordan canonical form fully described in control textbooks. To convert a given model (5.2a) and ((5.2b)) to some canonical form, use is made of a proper nonsingular linear (similarity) transformation 
, where 
is the new state vector.
Example 5.1
In this example, we derive the dynamic models (transfer function, state-space model) of the direct current (DC) electrical motor which is used in mobile robots to provide the torques that lead to the desired acceleration and velocity of them. DC motors are distinguished into motors controlled by the rotor (armature controlled), and motors controlled by the stator (field controlled). Both the motors will be considered.
Armature Controlled DC Motor
The rotor involves the armature and the commutator. A schematic of this motor is shown in Figure 5.2, where 
and 
are the resistance and inductance of the rotor, 
is the load moment of inertia, and 
is the linear friction coefficient.
Figure 5.2 Schematic of the armature controlled DC motor (
=rotation angle, 
=motor angular speed, 
=load moment of inertia).
The mechanical torque is given by:
(5.7)
where 
is the motor’s torque constant. The back electromotive force (emf) 
which is subtracted from the input voltage 
is proportional to 
, that is:
(5.8)
The characteristic curves of “
” are obtained by plotting the following function:
and have the linear form shown in Figure 5.3.
At the point where 
, the motor maintains a constant angular speed (assuming of course that no external disturbances affect the motor). The differential equation of the motor can be found using the following relations:
where 
, 
is the moment of inertia of the load (plus the moment of inertia of the motor), and 
is the linear friction coefficient, and eliminating 
. The result is:
where 
. If 
is negligible, then 
, and the above differential equation reduces to:
(5.9)
where 
is as above, and 
. In practice, the model in Eq. (5.9) represents an adequate approximation of the motor dynamics. The controllable state-space canonical model of the motor is found from Eq. (5.9) using Eqs. (5.3) and (5.6), that is:
(5.10)
with 
and 
. A DC motor is shown in Figure 5.4A. Figure 5.4B shows DC motors of several sizes.
Figure 5.4 (A) A heavy-duty DC robot motor. (B) Several DC motors with embedded gear boxes. Source: http://www.goldmine-elec-products.com/prodinfo.asp?number=0; http://www.robojrr.tripod.com/motortech.htm.
Field Controlled DC motor
In this motor, the rotor’s current is kept constant (coming from a constant-current source), whereas the error is fed to the magnetic field of the stator via a phase-sensitive amplifier (Figure 5.5). The characteristic curves 
show that when 
is not excessively large, the mechanical torque 
is independent of 
, depending only on the field current 
(Figure 5.5B).
Figure 5.5 (A) Field controlled DC motor. (B) Characteristic curves for different 
(for very large 
, we have a fall of 
).
A schematic of this motor is shown in Figure 5.6.
Here, we have the following relations:
(5.11)
where 
is the field current/torque constant and 
is the inductance of the stator, and all other symbols have the same meaning as in the armature controlled motor.
Combining the above equations we get:
(5.12)
where 
(DC gain), and 
, 
are the time constants of the magnetic field and the mechanical time constant of the motor, respectively, given by:
In practice, 
is much smaller than 
, and so Eq. (5.12) reduces to:
(5.13)
which is of the same form as Eq. (5.9). Therefore, the motor has the state-space model (similar to Eq. (5.10)):
with 
and 
. If the motor dynamics (Eq. (5.9) or (5.13)) is expressed in terms of the angular velocity 
, then (whenever the motor dynamics is not neglected) we use the form:
where 
or 
. This is analogous to a first-order RC circuit with time constant 
.
5.2.2 Lyapunov Stability
Stability is a binary property of a system, that is, a system cannot be simultaneously stable or not stable. However, a stable system is characterized by a degree or index that shows how much near to instability the system is (relative stability). A system is defined to be bounded-input bounded-output (BIBO) stable if any bounded input leads always to a bounded output. A linear time-invariant system is BIBO stable if and only if all the poles of its transfer function or the eigenvalues of the matrix 
of its state-space model (5.2a) and ((5.2b)) lie strictly on the left-hand complex semiplane 
. The matrix 
with the above property is called a Hurwitz matrix. The Routh and Hurwitz algebraic criteria specify the conditions that the coefficients of the system’s characteristic polynomial must satisfy in order for the system to be stable. A first-order system 
(with a real pole 
) is stable if 
, and has the impulse response:
Since 
tends to zero as 
, asymptotically, the system is said to be asymptotically stable. Furthermore, since the convergence is exponential, that is, according to 
, this system is called exponentially stable. For a second-order system where the matrix 
has the eigenvalues 
, 
, the impulse response has the form:
Since 
as 
, the system is asymptotically stable, and because 
, the system is exponentially stable. The above results hold for any combination of first-order and second-order systems.
The study of stability of a system and its stabilization via state or output feedback are two of the central problems in control theory. But the Routh and Hurwitz stability criteria can only be used for time-invariant linear single-input single-output (SISO) systems.
Lyapunov’s stability method can also be applied to time-varying systems and to nonlinear systems. Lyapunov has introduced a generalized notion of energy (called Lyapunov function) and studied dynamic systems without external input. Combining Lyapunov’s theory with the concept of BIBO stability we can derive stability conditions for input-to-state stability (ISS).
Lyapunov has introduced two stability methods. The first method requires the availability of the system’s time response (i.e., the solution of the differential equations). The second method, also called direct Lyapunov method, does not require the knowledge of the system’s time response.
Definition 5.1
The equilibrium state 
of the free system 
is stable in the Lyapunov sense (L-stable) if for every initial time 
and every real number 
, there exists some number 
as small as desired, that depends on 
and 
, such that: if 
, then 
for all 
, where 
denotes the norm of the vector 
, that is, 
.■
Theorem 5.1
The transition matrix 
of a linear system is bounded by 
for all 
if and only if the equilibrium state 
of 
is L-stable.■
The bound of 
of a linear system does not depend on 
. In general, if the system stability (of any kind) does not depend on 
, we say that we have global (total) stability or stability in the large. If the stability depends on 
, then it is called local stability. Clearly, total stability of a linear system implies also local stability.
Definition 5.2
is asymptotically stable if:
and 
sufficiently near to 
, the condition 
, for 
holds.■Definition 5.3
If the parameter 
in Definition 5.1 does not depend on 
, then we have uniform L-stability.■
Definition 5.4
If the system 
is uniformly L-stable, and for all 
and for arbitrarily large 
, the relation 
implies 
for 
, then the system is called uniformly asymptotically stable.■
Theorem 5.2
The linear system 
is uniformly asymptotically stable if and only if there exist two constant parameters 
and 
such that: 
for all 
and all 
.■
Definition 5.5
The equilibrium state 
of 
is said to be unstable if for some real number 
, some 
and any real number 
arbitrarily small, there always exists an initial state 
such that 
for 
.■
Figure 5.7 illustrates geometrically the concepts of L-stability, L-asymptotic stability, and instability.
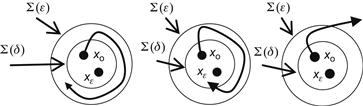
Figure 5.7 Illustration of L-stability (A), L-asymptotic stability (B), and instability (C). 
and 
symbolize n-dimensional balls (spheres) with radii 
and 
, respectively.
Direct Lyapunov method: Let 
be the distance of the state 
from the origin 
(defined using any valid norm). If we find some distance 
which tends to zero for 
, then we conclude that the system is asymptotically stable. To show that a system is asymptotically stable using Lyapunov’s direct method, we do not need to find such a distance (norm), but a Lyapunov function which is actually a generalized energy function.
Definition 5.6
Time-invariant Lyapunov function is called any scalar function 
of 
which for all 
and 
in the vicinity of the origin satisfies the following four conditions:1
is continuous and has continuous derivatives
for all 
Theorem 5.3
If a Lyapunov function 
can be found for the state of a nonlinear or linear system 
, where 
(
is a general function), then the state 
is asymptotically stable.■
Remarks
(i) If Definition 5.6 holds for all 
, then we have “uniformly asymptotic stability.”
(ii) If the system is linear, or we replace in Definition 5.6 the condition “
in the vicinity of the origin,” by the condition “
everywhere,” then we have “total asymptotic stability.”
(iii) If the condition (iv) of Definition 5.6 becomes 
, then we have (simple) L-stability.
Clearly, to establish L-stability of a system, we must find a Lyapunov function. Unfortunately, there does not exist a general methodology for this.
Analogous results hold for the case of time-varying Lyapunov functions 
, namely:
Definition 5.7
Time-varying Lyapunov function 
for the system’s state is any scalar function of 
and 
, which, for all 
and 
near the origin 
, has the following properties:
and its partial derivatives exist and are continuous
for 
and 
, where 
and 
is a scalar continuous non decreasing function of 
Remark
For all 
, the function 
should have values greater than or equal to the values of some continuous nonreducing time-invariant function.
Theorem 5.4
If a time-varying Lyapunov function 
can be found for the state 
of the system 
, then the state 
is asymptotically stable.■
Definition 5.8
(i) If the conditions of Definition 5.7 hold for all 
and 
, where 
is a continuous nondecreasing scalar function of 
with 
, then we have uniformly asymptotic stability.
(ii) If the system is linear or the conditions of Definition 5.7 hold everywhere (not only in a region of the origin 
), and if we have 
, when 
, then we say that the system is uniformly totally asymptotically stable.■
In the case of a linear time-varying system 
the Lyapunov (time varying) function 
is given by the quadratic (energy) function:
(5.14a)
where 
satisfies the following matrix differential equation:
(5.14b)
If the system is time-invariant 
, then 
and the above differential equation for 
reduces to the following algebraic equation for 
:
(5.15)
In this case, we can select a positive definite matrix 
and solve the 
equations (
is symmetric) for the elements of 
. Then, if 
(i.e., if 
is positive definite) the system is asymptotically stable.
5.2.3 State Feedback Control
State feedback control is more powerful than classical control because the design of a total controller for a multiple-input multiple-output (MIMO) system is performed in a unified way for all control loops simultaneously, and not serially one loop after the other which does not guarantee the overall system stability and robustness. In this section we will briefly review the eigenvalue placement controller for SISO systems.
Let a SISO system:
where 
is a 
constant matrix, 
is an 
constant matrix (column vector), 
is an 
matrix (row vector), 
is a scalar input, and 
is a scalar constant. In this case, a state feedback controller has the form:
(5.16)
where 
is a new control input and 
is an n-dimensional constant row vector: 
. Introducing this control law into the system, we get the state equations of the closed-loop (feedback) system:
(5.17)
The eigenvalue placement design problem is to select the controller gain matrix 
such that the eigenvalues of the closed-loop matrix 
are placed at desired positions 
. It can be shown that this can be done (i.e., the system eigenvalues are controllable by state feedback) if and only if the system 
is totally controllable. The concept of controllability has been developed to study the ability of a controller to alter the performance of the system in an arbitrary desired way. As it is known, the positions of the eigenvalues specify the performance characteristics of a system.
Definition 5.9
A state 
of a system is called totally controllable if it can be driven to a final state 
as quickly as desired independently of the initial time 
. A system is said to be totally controllable if all of its states are totally controllable.■
Intuitively, we can see that if some state variables do not depend on the control input 
, no way exists that can drive it to some other desired state. Thus, this state is called a noncontrollable state. If a system has at least one noncontrollable state, it is said to be nontotally controllable or, simply, noncontrollable. The above controllability concept refers to the states of a system and so it is characterized as state controllability. If the controllability is referred to the outputs of a system then we have the so-called output controllability. In general, state controllability and output controllability are not the same.
Theorem 5.5
The necessary and sufficient condition for a linear system 
to be totally state controllable is that the controllability matrix:
(5.18a)
has
(5.18b)
where 
is the dimensionality of the state vector 
.■
The most straightforward technique for selecting the feedback matrix 
is through the use of the controllable canonical form. This technique involves the following steps:
Step 1: We write down the characteristic polynomial 
of the matrix 
:
Step 2: Then, we find a similarity transformation 
that converts the given system to its controllable canonical form 
.
Step 3: From the desired eigenvalues of the closed-loop system, we determine the desired characteristic polynomial:
The feedback gain matrix 
of the controllable canonical model is given by:
Step 4: Equating the last rows of 
and 
we find:
we find:
(5.19)
5.2.4 Second-Order Systems
The state vector 
of a second-order system contains the position and velocity of the variable (physical quantity) of interest, namely:
Suppose that it is desired to design the state feedback controller such that the system’s state follows a desired trajectory 
. In this case, the feedback must use the measured error:2
(5.20)
and the controller should reduce the sensitivity of the system to the inaccuracy and the uncertainty in the parameter values used in the dynamic model.
A fundamental characteristic of control systems is the bandwidth 
which determines the operation speed of a system and capability of fast trajectory tracking. The greater the bandwidth is the better, but 
should not be very high because it may excite possible high-frequency components that have not been included in the system model.
As an example, consider the following simple second-order system:
(5.21)
which by Eq. (5.20) gives the error equation:
(5.22)
Defining the state vector:
we get the following controllable canonical form:
(5.23a)
where:
(5.23b)
To get a desired bandwidth 
, we select the desired closed-loop characteristic polynomial as:
(5.24)
where 
is the undamped natural frequency (taken equal to the desired bandwidth 
) and 
is the damping coefficient (usually selected 
).
Then, the feedback controller is selected as in Eqs. (5.16) and (5.19) with 
(unit matrix), namely:
or
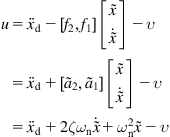(5.25)
The closed loop error system is obtained using Eqs. (5.22) and (5.25), that is:
(5.26)
which has the desired damping and bandwidth specifications.
The control law (5.25) contains the proportional term 
and the derivative term 
, that is, it is a PD (proportional plus derivative controller) which is one of the most popular and efficient controllers. For second-order systems, the PD controller gives exact results.
Example 5.2
Consider the case where the system (5.21) is corrupted by a disturbance 
as:
(a) It is desired to determine the steady-state position error 
of the closed-loop PD controlled system when 
is a step disturbance of amplitude 
:
(b) Show that this steady-state error vanishes if, instead of the PD controller, a PID (proportional plus integral plus derivative) controller is used.
Solution
(a) With the PD controller, the closed-loop disturbed system (5.26) becomes:
With 
and 
, the above step disturbance, the steady-state position error, obtained by setting 
and 
, satisfies the relation:
Thus:
We see that 
has a nonzero finite value which is proportional to 
and inversely proportional to the square of the bandwidth 
.
(b) If we use a PID controller:
the closed-loop error system becomes:
Then, in the limit as 
, for 
, 
and 
, 
we get:
which implies 
. Otherwise, 
cannot have a finite value.
Remark
The above results can also be obtained using the well-known Laplace transform final-value property 
and computing 
via the error system’s transfer function.
Example 5.3
It is desired to check the stability of the following systems using the Lyapunov method:
Solution
System (a): This system has the equilibrium state 
. We examine if the function 
is a Lyapunov function. This is done by checking if all conditions for 
to be a Lyapunov function are satisfied. We have:
and 
are continuous
for 
for all 
We see that all properties of the candidate function required to be a Lyapunov function hold, and so the system 
is uniformly asymptotically stable.
System (b): We try the following candidate Lyapunov function:
This function has the following properties:
and 
are continuous
for 
that is, it possesses all properties of a Lyapunov function. Therefore, the only equilibrium state 
(i.e., the origin) is totally asymptotically stable.
5.3 General Robot Controllers
The following general controllers, which are standard in robotics [2–4], will be examined:
• Proportional plus derivative control
• Lyapunov function based control
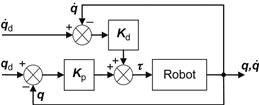
5.3.1 Proportional Plus Derivative Position Control
Here, it will be shown that PD control leads to satisfactory results in the control of the position of a general robot described in Eqs. (3.11a) and (3.11b):
where for any 
, 
is a known positive definite matrix. Assuming that the friction is negligible and omitting the gravity term 
, which anyway is zero in mobile robots moving on an horizontal terrain, we get:
(5.27)
where 
is defined as in Eq. (3.13), and the matrix 
is antisymmetric.
Let 
be the error between 
and 
. Then, the PD controller has the form
(5.28)
where 
and 
are positive definite symmetric matrices. The resulting feedback control scheme has the form of Figure 5.8.
Let us try the following candidate Lyapunov function:
(5.29)
where the term 
is the robot’s kinetic energy, and the term 
represents the proportional control term. Thus, the function 
can be considered as representing the total energy of the closed-loop system. Since 
and 
are symmetric positive definite matrices, we have 
and 
for 
. Therefore, we have to check the validity of property (iv) of Definition 5.6.
Here, Eq. (5.29) gives:
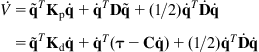(5.30)
Now, introducing the control law (5.28) into Eq. (5.30) we get:
(5.31)
Therefore, since the matrix 
is antisymmetric, Eq. (5.31) finally gives:
(5.32)
We observe that while the Lyapunov function 
in Eq. (5.29) depends on 
, its derivative 
depends on 
, which is analogous of the known property of classical SISO PD control. The condition (5.32) ensures that the feedback error control system (Figure 5.8) is L-stable. It is also useful to remark that the PD control (5.28) is particularly robust with respect to mass variations because it does not require knowledge of the parameters that depend on mass.
A special case of the controller (5.28) is:
which is applied to each joint separately. If the motion is subject to friction (assumed linear) the robot model (5.27) must simply be replaced by:
where 
is the diagonal matrix of friction coefficients. The present PD controller can be enhanced with an integral term as given in Example 5.2.
5.3.2 Lyapunov Stability-Based Control Design
The control design method applied to the above problem is known as Lyapunov-based controller design and constitutes a widely used method for both linear and nonlinear systems. The steps of this method are the following:
Step 1: Select a trial (candidate) Lyapunov function, which is typically some kind of energy-like function for the system, and possesses the first three properties of Lyapunov functions (Definition 5.6, Section 5.2.2).
Step 2: Derive the equation for the derivative 
along the system trajectory:
and select a feedback control law:
Typically, 
is a nonlinear function of 
that contains some parameters and gains which can be selected to make 
, and thus ensures that the closed-loop system is asymptotically stable.
Remark
For a given system, one may find several Lyapunov functions and corresponding stabilization controllers. If the system is linear time-invariant 
, then it is not necessary to work using the Lyapunov method. In this case, the controller is a static linear state feedback controller 
(Eq. (5.16)), which can be selected to make the closed-loop matrix a Hurwitz matrix (with all its eigenvalues on the strict left-hand s-plane). This assures that the closed-loop system is asymptotically and exponentially stable. The Lyapunov-based controller design method will be applied as a rule in most cases of the discussions that follow.
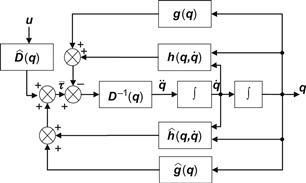
5.3.3 Computed Torque Control
The computed torque control technique reduces the effects of the uncertainty in all the terms of the Lagrange model. The controller 
is selected to have the same form as the dynamic model (Eq. (3.11a)), that is:
(5.33)
Thus, since the inertia matrix is positive definite (and so invertible), introducing the control law (5.33) in the system (3.11a), we get:
(5.34)
This implies that 
can be a decoupled controller (PD, PID) that can control each joint (motor axis) independently. The basic problem of the computed torque method is that we do not have available the exact values of 
, 
, and 
, but only approximate values 
, 
, and 
. Then, instead of Eq. (5.33) we get:
(5.35)
and so Eq. (5.34) is replaced by:
(5.36)
A problem with the model in Eq. (5.35) is the investigation of its robustness to modeling uncertainties which include uncertainties in the parameter values and nonmodeled high-frequency components (e.g., structural resonance, sampling rate, or omitted time delays). The computed torque control method belongs to the general class of linearization techniques via nonlinear state feedback (see Section 6.3). Solving the model (Eq. (3.11a)) for 
we get:
(5.37)
Introducing the controller (5.35) into (5.37) we obtain the block diagram of the overall closed-loop system shown in Figure 5.9.
5.3.4 Robot Control in Cartesian Space
The controllers presented thus far work in the joints’ (motors’) space and are based on the error 
between the actual and desired generalized joint variables 
(called internal variables). The motion of the robot in the Cartesian (or task, or working) space is obtained indirectly from the motion of the joints. However, in many cases, it is required to design the controller so as to work directly with the Cartesian variables, called external variables.
In Cartesian space, we have three types of controllers which are known as resolved motion controllers:
Here, we will study the resolved motion rate control which is mostly used in mobile robots. The resolved acceleration controller is actually an extension of the resolved motion rate control that includes the acceleration, a fact that will also be briefly considered.
5.3.4.1 Resolved Motion Rate Control
The resolved motion rate control is the control where the joints are moved simultaneously in different velocities, such that a desired motion in Cartesian (or task) space is obtained.
In general, the relation of the linear and angular velocity (motion rate) vector:
in Cartesian space and the velocities 
of the robotic joints is given by the Jacobian relation (Eq. (2.6)):
(5.38)
where the Jacobian matrix 
is given by Eq. (2.5), which has the inverse (see Eqs. (2.7b) and (2.8)):
(5.39a)
or the generalized inverse:
(5.39b)
Differentiating Eq. (5.38) we get:
(5.40)
Thus, introducing into Eq. (5.40) the expression of 
given by Eq. (5.39a) yields:
(5.41)
This relation gives the accelerations of the joints for given linear/angular velocity and acceleration of the robot end-effector in Cartesian space. If 
is not square, we use the generalized inverse 
in place of 
.
The block diagram of the resolved velocity control is shown in Figure 5.10.
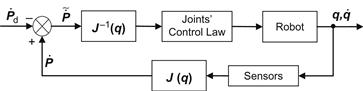
Figure 5.10 Block diagram of the robot resolved rate control based on Eq. (5.39a).
In the simplest case, the joints control can be a proportional control law with gain 
. In many cases, the task space control is required to be in a coordinate frame attached to the robot (and not in the world coordinate frame). The velocity 
is then given by:
(5.42)
where 
is the desired velocity of the robot and 
is a matrix that relates 
to 
. Then, from Eqs. (5.39a) and (5.39b) we get:
(5.43)
The relation (5.43) is typically used in vision-based robot control (visual servoing).
5.3.4.2 Resolved Motion Acceleration Control
The resolved motion acceleration control method is based on the equation:
(5.44)
which is found by differentiating Eq. (5.38). The desired position, velocity, and acceleration of the robot in Cartesian space are assumed to be known from the trajectory planner. Thus, to reduce the position error, we must apply appropriate forces/torques at the robot joints, such that the acceleration in Cartesian space satisfies the relation:
(5.45)
where 
, and 
are the desired translation position, velocity, and acceleration, respectively.
Here, the position error is:
Therefore, in terms of 
, Eq. (5.45) is written as:
(5.46)
and the gains 
should be selected such that 
tends asymptotically to zero. A similar error equation can be derived for the angular acceleration 
, using the control law:
(5.47)
where 
is the orientation angle in the Cartesian space. Combining Eqs. (5.45) and (5.47), and inserting into Eq. (5.44), we get:
(5.48)
where:
Equation (5.48) constitutes the basis for the resolved motion acceleration control of robots. The position 
and velocity 
are measured by potentiometers or optical encoders.
5.4 Control of Differential Drive Mobile Robot
The control procedure will involve two stages:
The resulting linear and angular velocities in the kinematic stage will be used as reference inputs for the dynamic stage. Thus, this procedure belongs to the general class of backstepping control [5–13].
5.4.1 Nonlinear Kinematic Tracking Control
The robot motion is governed by the dynamic model (Eqs. (3.23a) and (3.23b), the kinematic model (Eq. (2.26)), and the nonholonomic constraint (Eq. (2.27)), namely:
(5.49a)
(5.49b)
(5.49c)
where, for notational simplicity, the index 
was dropped from 
, 
and 
, 
, 
are the control inputs, with:
(5.49d)
being the state vector.
The problem is to track a desired state trajectory:
(5.50)
with error that goes asymptotically to zero.
To this end, the Lyapunov stabilizing method will be used. For realizability, the desired trajectory must satisfy both the kinematic equations and the nonholonomic constraint, that is:3
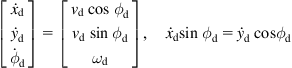(5.51)
The errors 
, 
, and 
, expressed in the wheeled mobile robots’ (WMR’s) local (moving) coordinate frame 
, are given by (see Eq. (2.17)):
(5.52a)
and
(5.52b)
Differentiating Eqs. (5.52a) and (5.52b) and taking into account Eqs. (5.49c) and (5.51), we get the following kinematic model for the error 
:
(5.53)
where the linear and angular velocities 
and 
are the kinematic control variables. Clearly, Eq. (5.53) satisfies the kinematic and nonholonomic equations of the WMR.
Therefore, the kinematic feedback controller will be based on Eq. (5.53). The Lyapunov stabilizing method of Section 5.3.2 will be applied. Since here the controller should be nonlinear, we cannot select its structure beforehand. Its structure will be determined by the choice of the candidate Lyapunov function. Here, the following candidate function is selected [14]:
(5.54)
This function satisfies the first three properties of Lyapunov functions, namely:
is continuous and has continuous derivatives
for all 
We therefore have to check under what conditions the fourth property can be satisfied.
Differentiating Eq. (5.54) with respect to time we get:
(5.55)
To make 
, the control inputs 
and 
are selected such that:
(5.56)
which leads to:
(5.57a)
(5.57b)
Clearly, for 
and 
, we have 
with the equality obtained only when 
and 
. Thus, the controller (5.57a) and ((5.57b) guarantees total asymptotic tracking to the desired trajectory.
Remark 1
We can also add a gain 
in the second term of Eq. (5.56b), that is, choose 
as
(5.58a)
In this case, total asymptotic tracking to the desired trajectory 
can be proved using the following Lyapunov function:
(5.58b)
Remark 2
A more general kinematic controller can be obtained by using the Lyapunov function:
(5.58c)
with 
, 
, and 
. In the following, we will derive this controller. To this end, we define new control variables 
, 
and write the model (5.53) as:
(5.58d)
Differentiating Eq. (5.58c) and using the model (5.58d) we get:
To assure that 
, we use two functions 
and 
for all 
, and select 
and 
such that:
(5.58e)
Then, it follows that:
The above controller assures that 
and 
. Since 
is uniformly continuous, Barbalat’s Lemma (Sec. 6.2.3) implies that 
. This by Eq. (5.58e) implies that 
and 
. Now, obviously, 
(i.e., 
). One way to overcome the fact that 
does not converge only to 0 but also to 
is to take care that the WMR, before trying to track immediately the desired trajectory (i.e., the virtual WMR), is rotating about its own axis with an increasing angular velocity 
until it sees the virtual robot. The reader can verify that this can be done by the controller [11]:
where 
is given by the dynamic model:
with 
being a step input function defined by:
5.4.2 Dynamic Tracking Control
Having selected 
and 
as in Eqs. (5.57a) and (5.57b) (or Eq. (5.58a)), we select the control inputs (torques) 
and 
in Eq. (5.49a) as:
(5.59a)
(5.59b)
where:
(5.59c)
Introducing Eqs. (5.59a)–(5.59c) into Eqs. (5.49a) and (5.49b) we get the velocities’ error equations:
which for 
and 
are stable and 
, 
converge to zero asymptotically. Therefore, in selecting the feedback control inputs (torques) as in Eqs. (5.59a) and (5.59b) with 
and 
given by Eqs. (5.57a) and (5.57b), the tracking of the desired trajectory 
is achieved asymptotically, as required. The block diagram of the feedback tracking controller is depicted in Figure 5.11.
5.5 Computed Torque Control of Differential Drive Mobile Robot
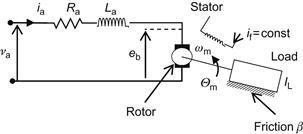
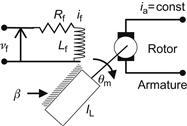
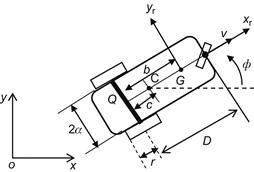
The control design procedure involves again two stages: kinematic control followed by dynamic control. We will work on the WMR shown in Figure 5.12, where the motor dynamics includes a gear box (of ratio N) [13].
traced by the controller is different than 
and 
.Here, Q is the midpoint of wheel baseline, G the center of gravity, and C the point traced by the controller (different than the point Q).
The meaning of the remaining symbols are self-evident (the same as in Figure 2.7).
5.5.1 Kinematic Tracking Control
The kinematic equations of the robot are:
(5.60a)
(5.60b)
(5.60c)
where 
is the lateral velocity in the local coordinate frame 
.
Equations (5.60a) and (5.60b) are written in the matrix form:
Now, using new control variables 
and 
defined by:
(5.61)
(5.62)
The dynamic system (5.62) is linear and decoupled, and so the state-feedback law:
(5.63)
yields the error dynamics:
(5.64)
with 
and 
.
Therefore, from Eq. (5.64), it follows that for any positive gains:
the tracking error tends exponentially to zero.
Combining Eqs. (5.61) and (5.63) we get the overall nonlinear kinematic control law:
(5.65)
5.5.2 Dynamic Tracking Control
The feedback kinematic controller (5.65) incorporates the WMR kinematic equations and so one can now use the reduced (unconstrained) dynamic model ((3.19a) and (3.19b)) of the robot for the selection of the control inputs (motor torques or motor voltages), as described in Section 5.4.2, where actually the computed torque method was applied.
For the robot of Figure 5.12, with the motor dynamics included, the reduced model has the following form:
(5.66)
where:
(5.67)
(5.68)
=combined wheel, motor rotor, and gearbox inertia
=combined wheel, motor, and gearbox friction coefficient
=right and left wheel motor voltage
=electrical resistance
=motor voltage/torque constantsNow, applying the computed torque (linearization) technique to Eq. (5.66), we choose the voltage control vector 
as:
(5.69)
where 
is the new control vector. Introducing Eq. (5.69) into Eq. (5.66) we get:
with:
Therefore, selecting the linear state feedback control law:
(5.70)
which for 
is asymptotically stable with equilibrium state 
.
Combining Eq. (5.69) with Eq. (5.70), we get the full dynamic controller:
(5.71)
The overall tracking controller of the robot is given by Eqs. (5.65) and (5.71).
Example 5.4
It is desired to formulate and solve the kinematic problem of a unicycle-like WMR to go asymptotically from an initial state (position and orientation) to a goal state (position and orientation) using polar coordinates.
Solution
The unicycle-like robots are described by the kinematic Eq. (2.26):
(5.72)
where 
is the velocity and 
is the angle of the WMR 
axis with the goal (world) coordinate frame x-axis. All WMRs with the above kinematic equations, for example, the differential drive WMR, are said to belong to the unicycle-like class of mobile robots. The geometry of the WMR that will be used for formulating the polar coordinates is shown in Figure 5.13 [15].
Figure 5.13 Polar coordinates of the unicycle. Here, the goal coordinate frame Gxy is considered to be the world coordinate frame.
The kinematic control variables of the robot are 
and 
. The polar coordinates (position and orientation) of the WMR are its distance 
from the goal, and its orientation 
with respect to the goal’s coordinate frame Gxy. The steering angle is 
. Then, in polar coordinates, the kinematic model in Eq. (5.72) is replaced by:
(5.73a)
(5.73b)
(5.73c)
These relations hold for 
, a condition which will be always satisfied by an asymptotic reduction of 
to zero (since for any finite time there always be 
).
Our goal tracking control problem is to find a state-feedback law:
(5.74)
which guarantees that 
, 
, and 
, asymptotically.
To this end, we will apply the Lyapunov-based control method. Let us choose the following candidate Lyapunov function [15]:
(5.75)
Clearly, the function 
possesses the first three properties of Lyapunov functions. We will determine the controller (5.74) which will assure that the fourth property 
is also possessed by 
, along the system trajectory.
The time derivative of 
, along the trajectory determined by Eqs. (5.73a)–(5.73c), is found to be:
(5.76a)
where:
(5.76b)
(5.76c)
Choosing 
as:
(5.77)
yields:
(5.78)
Now, introducing Eq. (5.77) into Eq. (5.76c) we get:
Thus, selecting 
as:
(5.79)
yields:
(5.80)
The inequalities (5.78) and (5.80) give:
(5.81)
This implies, by the Lyapunov stability theorem, that 
and 
go asymptotically to zero for any 
. Thus, we have to see what happens to 
. To this end, we get the closed-loop system kinematics by introducing the control laws (5.77) and ((5.79)) into Eqs. (5.73a)–(5.73c), namely:
(5.82a)
(5.82b)
(5.82c)
These equations show that the asymptotic convergence of 
and 
to zero implies the asymptotic convergence of 
to its only equilibrium state 
. In fact, from Eq. (5.82c) it follows that 
implies 
, that is, 
tends to some finite value 
. Then, we see from Eq. (5.82b) that the uniformly continuous function 
tends necessarily to 
.4 On the other hand, by Barbalat’s lemma, 
tends to zero, which in turn implies that 
(see Section 6.2.3). Therefore, the smooth kinematic control laws (5.77) and ((5.79)) assure the asymptotic tracking of the goal position and orientation by the WMR, as desired. The fact that the control laws (5.77) and ((5.79)) are continuously differentiable does not contradict Brockett’s Theorem 6.6 and its corollary (c) because this theorem is valid for the Cartesian state-space representation (Eq. (5.72)) of the unicycle-like WMR [15].
4Recall that 
as 
.
5.6 Car-Like Mobile Robot Control
For the car-like WMR, we will study the following two representative problems:
5.6.1 Parking Control
Consider a car-like WMR (Figure 2.9) which controls the steering angle 
and the rear-wheels’ velocity 
. The orientation of the car body (i.e., of 
) is 
. The kinematic equations of the robot are given by Eq. (2.52):
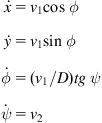(5.83)
The problem is to control the WMR (using 
and 
) so as to move it to a desired parking position and orientation, which here is assumed to be 
, 
, and 
(as it was actually done in Example 5.4 for the unicycle WMR). Here, this problem will be solved by a two-step maneuver to overcome the turning radius limitation of the car-like mobile robot, namely [16]:
and 
and 
Use of the Lyapunov-based control method will again be made as usual.
Step 1:
control
We select the following candidate Lyapunov function:
which satisfies the first three conditions of Lyapunov functions. We will check if the third condition can be satisfied, along the trajectory of the system in Eq. (5.83). We have:
(5.84)
Choosing:
(5.85)
and introducing into Eq. (5.84) yields:
(5.86)
which, by Lyapunov theorem, implies that 
tends asymptotically to zero.
The closed loop kinematics equation is:
(5.87)
Let 
. For 
to stay zero, 
should be zero. Then, Eq. (5.87) implies that 
should also tend to zero, for 
.
The change of the sign of 
is needed when the WMR cannot move with its current velocity due to the presence of obstacles or when the measured states exceed some predetermined bounds. Of course, the initial selection of 
affects the efficiency of the path. Actually, the controller (5.85) is a nonlinear bang-bang controller. Therefore, a switching rule is needed to determine when the change from 
to 
must occur.
Defining 
, the switching rule is:
; otherwise 
This rule means that if the front part of the WMR is closer to the origin, then it will go forward or backward.
Step 2:
control
We use the same form of the candidate Lyapunov function:
with 
and 
.
The time derivative 
along the trajectory of Eq. (5.83) is:
Choosing:
(5.88)
gives:
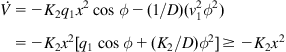(5.89)
which is negative semidefinite for 
.
For 
, in which case, by Eq. (5.88), 
, we have
Therefore, the mobile robot is uniformly L-stable at 
. However, 
cannot converge without increasing 
, a fact which is due to the low bound of the WMR turning radius (Figure 5.14A) [16,17]. Actually, 
can be made arbitrarily small at the first step. Therefore, when we achieve a very small 
(i.e., 
), we use 
, and 
.
Figure 5.14 (A) For 
to converge, 
must be increased. (B) Case 
. (C) Case 
. (D) Convergence to the origin 
using Eq. (5.90).
This situation is overcome if we use the transformation [16]:
(5.90)
In this way, the distance from the origin to the WMR is equal to the error of 
, and the difference angle of the WMR with the x-axis becomes the error of 
. As shown in Figure 5.14D, the controller (5.88) with the above switching type transformation assures that the WMR can go to 
starting from any initial posture.
5.6.2 Leader–Follower Control
Consider two car-like robots that follow a path with the first car acting as the leader and the second being a follower (Figure 5.15). For more WMRs, one following the other in front of it, this problem is known as formation control [7].
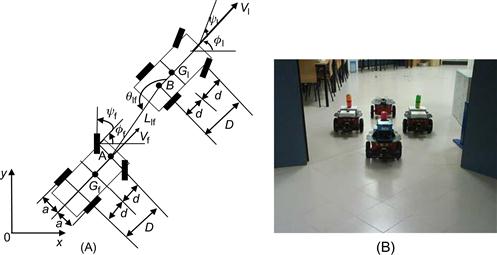
Figure 5.15 (A) Two car-like WMRs (leader–follower structure). (B) Four WMRs in a typical formation (diamond structure). Source: www.robot.uji.es/lab/plone/research/pnebot/index_html2.
The leader–follower control problem under consideration is to find a velocity control input for the follower that assures convergence of the relative distance 
and relative bearing angle 
of the WMRs to their desired values, under the assumption that the leader motion is known and is the result of an independent control law [7]. To solve the problem, we will apply the Lyapunov-based control design method using the kinematic and dynamic equations of the bicycle equivalent presented in Section 3.4 (see Eqs. (3.56), (3.57), (3.60a)–(3.60d)).
In Figure 5.15, 
, 
, and 
are the linear velocity, orientation angle, and steering angle of the leader, and 
, 
, 
are the respective variables of the follower. The coordinates of points 
and 
are denoted by 
and 
.
We first derive the dynamic equations for the errors:
(5.91)
where 
, 
, and 
represent the desired trajectory of the follower in world coordinates, which are transformed to 
, 
, and 
in the local coordinate frame of the follower. From Figure 5.15 we get:
(5.92a)
(5.92b)
(5.92c)
(5.92d)
Differentiating Eqs. (5.92b) and (5.92c) gives:
(5.93a)
(5.93b)
with (see Eqs. (3.56) and (3.57)):
(5.93c)
where 
.
Using Eqs. (3.56) and (5.93c) in Eqs. (5.93a) and (5.93b), we obtain:
(5.94a)
(5.94b)
while from Figure 5.13 we have:
(5.95)
Then, differentiating Eqs. (5.92a) and (5.92d), introducing Eqs. (5.94a) and (5.94b), and using the auxiliary variable:
we get, after some algebraic manipulation:
(5.96a)
(5.96b)
Using Figure 5.15, the actual and desired coordinates of the follower’s point A can be expressed in terms of the coordinates of the leader’s point B. Therefore, we use the variables 
and 
and get the error equations (in the world coordinate frame):
(5.97a)
(5.97b)
(5.97c)
Finally, differentiating Eqs. (5.97a)–(5.97c), we obtain the dynamic equations for 
, 
, and 
:
(5.98a)
(5.98b)
(5.98c)
We are now ready to apply the usual two-stage (kinematic, dynamic) backstep controller design.
5.6.2.1 Kinematic Controller
We select the candidate Lyapunov function [7]:
(5.99)
which is similar to Eq. (5.54), which possesses the first three properties of Lyapunov functions. The feedback control inputs 
and 
will be selected such that to make 
. Differentiating Eq. (5.99) gives:
(5.100)
Introducing Eqs. (5.98a)–(5.98c) into Eq. (5.100), we find that the selection of 
and 
as:
(5.101a)
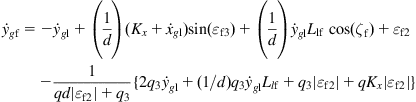(5.101b)
with 
makes 
. Indeed, introducing Eqs. (5.98a)–(5.98c), (5.101a), and (5.101b) into Eq. (5.100) yields:
, choosing 
, 
, and 
makes 
.5.6.2.2 Dynamic Controller
Use will be made of the dynamic model (Eqs. (3.60a)–(3.60d)). The desired velocity and steering angle 
, 
of the follower are given by the results of the kinematic controller. We define the error:
(5.102)
From Eqs. (3.60a)–(3.60c), applied to the follower WMR, we get:
(5.103)
where 
is the driving torque of the steering wheel of radius 
, and the relation 
was used. Combining Eqs. (5.103) and (3.60d) gives:
(5.104)
where:
Subtracting both sides of Eq. (5.104) from 
we get:
Now, adding and subtracting 
to the right-hand side of this equation yields:
(5.105a)
where:
(5.105b)
:The torque 
in Eq. (5.105a) can be found using the computed torque technique as:
(5.106)
which is introduced into Eq. (5.105a) to give the closed-loop error equation:
(5.107)
It only remains to select 
such that 
tends to zero asymptotically. We select the candidate Lyapunov function:
(5.108)
where 
is given by Eq. (5.99).
Differentiating 
and introducing the result into Eq. (5.107) gives:
Since 
by the kinematic controller design, we can assure that 
by selecting the gain matrix 
such that the matrix 
is positive definite, that is:
with 
and 
. Then, we find:
This implies that the error 
in Eq. (5.105a) tends asymptotically to zero, that is, 
and 
, as required. The function 
in the control law Eq. (5.106) can be approximated by a neural network using a weight updating rule as described in Section 8.5 [7].
5.7 Omnidirectional Mobile Robot Control
We will consider the three-wheel omnidirectional dynamic robot model (Eqs. (3.77a) and (3.77b)) derived in Section 3.5:
(5.109)
and will apply the resolved motion acceleration technique, combined with PI or PD control [18]. Solving Eq. (5.109) for 
, we get the inverse dynamic resolved acceleration equations:
(5.110a)
(5.110b)
(5.110c)
where:
(5.111a)
(5.111b)
(5.111c)
with:
being the errors between the desired and actual trajectories, and 
, 
, 
being proportional gains, 
, 
integral gains, and 
the derivative (velocity) gain of 
. Note that the factors 
and 
in Eqs. (5.110a)–(5.110c) are always nonzero (see Eqs. (3.76a)–(3.76c)) and so the above resolved acceleration controllers 
, 
, and 
exist for all 
.5
The block diagram of the overall feedback control WMR system is shown in Figure 5.16.
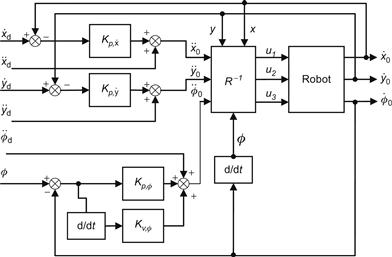
Figure 5.16 Resolved acceleration control system for the three-wheel omnidirectional robot (
represents the robot inverse dynamics Eqs. (5.110a)–(5.110c)).
The above controller was applied to a real robot with physical parameters:
The initial state used is:
A basic experiment was to check the WMRs holonomic property, that is, the ability of the robot to independently achieve translational and rotational motion around the center of gravity in the x-y plane.
To check this property, it was assumed that the robot must travel with a single azimuth 
(see Figure 3.6) for 20 s, but with zero rotational angle for 0–10 s, and a uniformly varying rotational angle from 
to 
for 10–20 s. Although the moving velocity was to be 
in the steady state, a sinusoidal reference velocity was set for each 2 s at the starting and ending period. Using these 
and 
values, the corresponding 
and 
were derived from:
where the positive rotational direction of motion is the counterclockwise direction. The desired accelerations 
and 
were derived by differentiation of 
and 
. A selection of the gains used is given in Table 5.1.
The responses obtained for 
, 
, and 
, and the (x,y) trajectory are shown in Figure 5.17.
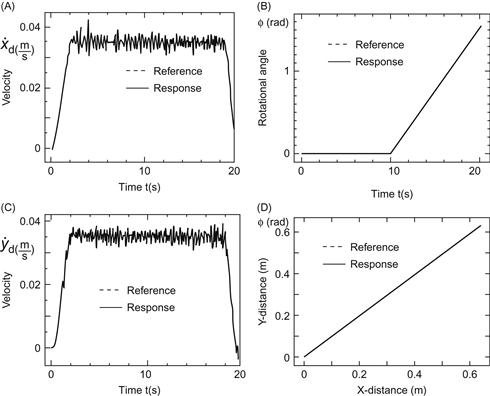
Figure 5.17 (A,C) Actual velocity responses compared to the desired velocity responses 
and 
. (B) Trajectory of 
, (D) (x,y) trajectory. Source: Reprinted from Ref. [18], with permission from Springer Science+Business Media BV.
We observe that despite the occurrence of some oscillations in the velocities 
and 
, the 
trajectory matches perfectly the desired trajectory 
. Another experiment was carried out to follow a circular path with a radius less than half the distance between the wheels (say 0.1 m with distance between the wheels 0.356 m). Using the same gains as before, the results were very good, with perfect tracking of the circular path [18].
Example 5.5
Apply the computed torque technique to derive a PD path tracking controller for a three-wheel omnidirectional robot.
Solution
We will work with the dynamic model derived for the omnidirectional robot of Figure 3.7 in Example 3.2, namely:
(5.112)
The computed torque control law has the form (Eq. (5.33)):
(5.113)
and the PD control has the form:
(5.114)
where:
(5.115)
is the tracking error of the resulting path from the desired path 
. Combining Eqs. (5.113) and (5.114) and introducing into Eq. (5.112), we get the closed-loop system:
or the tracking error dynamic equation:
(5.116)
since the matrix 
is nonsingular. We see that the origin 
is an equilibrium point of this system. Therefore, selecting proper values of 
and 
, we can assure that 
tends to zero, that is, 
, asymptotically. To this end, we use the following candidate Lyapunov function:
(5.117)
which, for sufficiently small constant 
, satisfies the first two properties of Lyapunov functions.
We will now examine under what conditions 
is negative. The time derivative of 
along the trajectory of 
is found to be:
Choosing 
and 
(positive definite), we get 
and so 
asymptotically.
The performance of the controller was tested on the WMR of Section 5.7 with the same values of physical parameters and the same desired path using the PD gains given in Table 5.2.
The responses obtained for the 
and 
trajectories are similar to those shown in Figure 5.17. As an exercise, the reader may test the performance of the controller for a circular desired path with a given radius 
(e.g., 
). A parameterized form of the circle equation, namely, 
, 
can be used where 
is the angle of the point 
with reference to the x-axis of the world coordinate frame. In this case, a suitable polynomial or other series representation of the angle 
can be used. A more complex desired path that might be examined is an 8 shaped path of a given size.
References
1. Ogata K. State space analysis of control systems Upper Saddle River, NJ: Prentice Hall; 1997.
2. Asada H, Slotine JJ. Robot analysis and control New York, NY: Wiley; 1986.
3. Spong MW, Vidyasagar M. Robot dynamics and control New York, NY: Wiley; 1989.
4. Wolovich W. Robotics: Basic Analysis and Design. Birmingham, UK: Holt Rinehart and Winston, Dreyden Press;1987.
5. Kanayama Y, Kimura Y, Noguchi T. A stable tracking control method for a nonholonomic mobile robot. IEEE Trans Robot Autom. 1991;7:1236–1241.
6. Yiaoping Y, Yamamoto Y. Dynamic feedback control of vehicles with two steerable wheels. Proceedings of IEEE international conference on robotics and automation. Minneapolis, MN; 1996. 12(1), p. 1006–1010.
7. Panimadai Ramaswamy SA, Balakrishnan SN. Formation control of car-like mobile robots: a Lyapunov function based approach. Proceedings of 2008 American Control Conference. Seattle, Washington; June 11–13, 2008.
8. Tian Y, Sidek N, Sarkar N. Modeling and Control of a nonholonomic wheeled mobile robot with wheel slip dynamics. Proceedings of IEEE symposium on computational intelligence in control and automation. Nashville, TN; March 30–April 2, 2009. p. 7–14.
9. Chang CF, Huang CI, Fu LC. Nonlinear control of a wheeled mobile robot with nonholonomic constraints. Proceedings of 2004 IEEE International conference on systems, man, and cybernetics. The Hague, The Netherlands; October 10–13, 2004. p. 5404–9.
10. Samson C, Ait Abderrahim K. Feedback control of nonholonomic wheeled cart in Cartesian space. Proceedings of IEEE Conference on robotics and automation. Sacramento, CA; 1990. p. 1136–41.
11. Velagic J, Lacevic B, Osmic N. Nonlinear motion control of mobile robot dynamic model. [Chapter 27] In: Jing X-J, ed. Motion Planning. In Tech, Open Books 2008;534–556.
12. Zhang Y, Hong D, Chung JH, Velinsky SA. Dynamic model based robust tracking control of a differentially steered wheeled mobile robot. Proceedings of american control conference (ACC ’88). Philadelphia, PA; June 1988. p. 850–5.
13. Ashoorizad M, Barzamini R, Afshar A, Zouzdani J. Model reference adaptive path following for wheeled mobile robots. Proceedings of international conference on information and automation (IEEE/ICIA’06). Colombo, Sri Lanka; 2006. p. 289–94.
14. Gholipour A, Dehgham SM, Ahmadabadi MN. Lyapunov based tracking control of nonholonomic mobile robot. Proceedings of 10th Iranian conference on electrical engineering. Tabeiz, Iran; 2002. 3, p. 262–69.
15. Aicardi M, Casalino G, Bicchi A, Balestrino A. Closed-loop steering of unicycle-like vehicles via Lyapunov techniques. IEEE Robot Autom Mag. 1995;March:27–35.
16. Lee S, Kim M, Youm Y, Chung W. Control of a car-like mobile robot for parking problem. Proceedings of 1999 IEEE international conference on robotics and automation. Detroit, MI; May 1999. p. 1–5.
17. Lee S, Youm Y, Chung. Control of car-like mobile robots for posture stabilization. Proceedings IEEE/RSJ international conference on intelligent robots and systems (IROS’99). Kyongju, Korea; October 1999. p. 1745–50.
18. Watanabe K, Shiraishi Y, Tang J, Fukuda T, Tzafestas SG. Autonomous control for an omnidirectional mobile robot with feedback control system. [Chapter 13] In: Tzafestas SG, ed. Advances in intelligent autonomous systems. Boston / Dordrecht: Kluwer; 1999;289–308.
1Note that here 
is considered to be a column vector, that is, 
.
2It is remarked that the error 
can also be defined as 
. In this case, the feedback gains have opposite signs and actually lead to the same negative feedback controller (Section 5.3.1).
3This is equivalent to considering that our WMR has to track a similar (virtual) differential-drive WMR which is moving with linear velocity 
and angular velocity 
.
5All the coordinates are those of the center of gravity (and symmetry) Q. The index Q was dropped for notational simplicity.