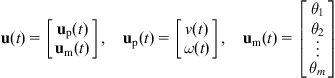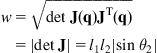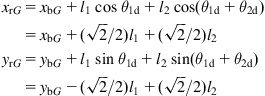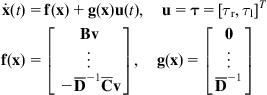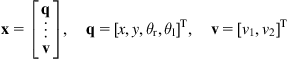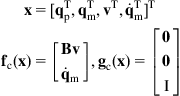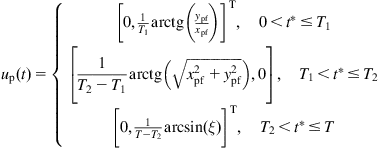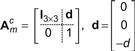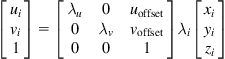Mobile Manipulator Modeling and Control
Mobile manipulators (MMs) are robotic systems consisting of articulated arms (manipulators) mounted on holonomic or nonholonomic mobile platforms. They provide the dexterity of the former and the workspace extension of the latter. They are able to reach and work over objects that are initially outside the working space of the articulated arm. Therefore, MMs are appealing for many applications, and today they constitute the main body of service robots. One of the principal and most challenging problems in MMs research is to design accurate controllers for the entire system.
The objectives of this chapter are (i) to present the Denavit–Hartenberg method of articulated robots’ kinematic modeling, and provide a practical method for inverse kinematics, (ii) to study the general kinematic and dynamic models of MMs, (iii) to derive the kinematic and dynamic models of a differential drive and a three-wheel omnidirectional MM, with two-link and three-link mounted articulated arms, respectively, (iv) to derive a computed-torque controller for the above differential-drive MM, and a sliding-mode controller for the three-wheel omnidirectional MM, and (v) to discuss some general issues of MM visual-based control, including a particular indicative example of hybrid coordinated (feedback/open-loop) visual control, and an omnidirectional (catadioptric) visual robot control example.
Keywords
Mobile manipulator modeling; mobile manipulator control; manipulability; omnidirectional mobile manipulator modeling; nonholonomic mobile manipulator modeling; differential-drive mobile manipulator control; full-state mobile manipulator visual control; mobile manipulator control; maximum manipulability
10.1 Introduction
Mobile manipulators (MMs) are robotic systems consisting of articulated arms (manipulators) mounted on holonomic or nonholonomic mobile platforms. They provide the dexterity of the former and the workspace extension of the latter. They are able to reach and work over objects that are initially outside the working space of the articulated arm. Therefore, MMs are appealing for many applications, and today they constitute the main body of service robots [1–27]. One of the principal and most challenging problems in MMs research is to design accurate controllers for the entire system. Due to the strong interaction and coupling of the mobile platform subsystem and the manipulator arm(s) mounted on the platform, a proper coordination between the respective controllers is needed [18,23]. However, in the literature there are also available unified control design methods that treat the whole system using the full-state MM model [3,10,22,24]. In either case the control methods studied in this book (computed-torque control, feedback linearizing control, robust sliding-mode or Lyapunov-based control, adaptive control, and visual-based control) can be employed and combined.
The objectives of this chapter are as follows:
• To present the Denavit–Hartenberg method of articulated robots’ kinematic modeling, and provide a practical method for inverse kinematics
• To study the general kinematic and dynamic models of MMs
• To derive the kinematic and dynamic model of a differential drive, and a three-wheel omnidirectional MM, with two-link and three-link mounted articulated arms, respectively
• To derive a computed-torque controller for the above differential-drive MM, and a sliding-mode controller for the three-wheel omnidirectional MM
• To discuss some general issues of MM visual-based control, including a particular indicative example of hybrid coordinated (feedback/open-loop) visual control and a panoramic visual servoing example.
10.2 Background Concepts
Here, the following aspects which will be used in the chapter are considered:
• The Denavit–Hartenberg direct manipulator kinematics method
• A general method for inverse manipulator kinematics
• The manipulability measure concept
• The two-link manipulator’s direct and inverse kinematic model and manipulability measure.
10.2.1 The Denavit–Hartenberg Method
The Denavit–Hartenberg method provides a systematic procedure for determining the position and orientation of the end-effector of an n-joint robotic manipulator, that is, for computing ![]() in (2.18).
in (2.18).
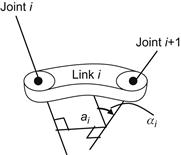
Consider a link ![]() that lies between the joints
that lies between the joints ![]() and
and ![]() of a robot as shown in Figure 10.1.
of a robot as shown in Figure 10.1.
Each link is described by the distance ![]() between the (possibly nonparallel) axes
between the (possibly nonparallel) axes ![]() and
and ![]() of the two joints, and the rotation angle
of the two joints, and the rotation angle ![]() from the axis
from the axis ![]() to the axis
to the axis ![]() with respect to the common normal of the two axes. Each joint (prismatic or rotary) is driven by a motor (translational or rotational) that produces the motion of link
with respect to the common normal of the two axes. Each joint (prismatic or rotary) is driven by a motor (translational or rotational) that produces the motion of link ![]() . In overall, the robotic arm has
. In overall, the robotic arm has ![]() joints and
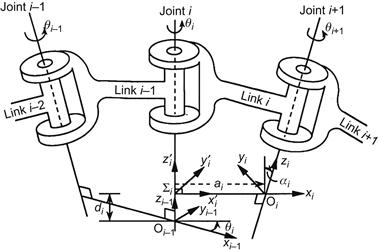
joints and ![]() links. The functional relation of the end-effector and the displacements of the joints can be found using the convention of parameters shown in Figure 10.2, called the Denavit–Hartenberg parameters.
links. The functional relation of the end-effector and the displacements of the joints can be found using the convention of parameters shown in Figure 10.2, called the Denavit–Hartenberg parameters.
These parameters refer to the relative position of the coordinate frames ![]() and
and ![]() , and are the following:
, and are the following:
• The length ![]() of the common normal
of the common normal ![]()
• The distance ![]() between the origin of
between the origin of ![]() and the point
and the point ![]()
• The angle ![]() between the joint
between the joint ![]() (i.e., the axis
(i.e., the axis ![]() ) and the axis
) and the axis ![]() in the positive (clockwise) direction
in the positive (clockwise) direction
• The angle ![]() between the axis
between the axis ![]() and the common normal (i.e., rotation about the axis
and the common normal (i.e., rotation about the axis ![]() ) in the positive direction.
) in the positive direction.
On the basis of the above, the transfer from the frame ![]() to the frame
to the frame ![]() can be done in four steps:
can be done in four steps:
Step 1: Rotation of frame ![]() about the axis
about the axis ![]() by an angle
by an angle ![]() .
.
Step 2: Translation of frame ![]() along the axis
along the axis ![]() by
by ![]() .
.
Step 3: Translation of the rotated axis ![]() (which now coincides with
(which now coincides with ![]() ) along the common normal by
) along the common normal by ![]() .
.
Denoting by ![]() the result of steps 3 and 4 and by
the result of steps 3 and 4 and by ![]() the result of steps 1 and 2, the overall result of steps 1 through 4 is given by:
the result of steps 1 and 2, the overall result of steps 1 through 4 is given by:
 (10.1)
(10.1)
where ![]() gives the position and orientation of the frame
gives the position and orientation of the frame ![]() with respect to the frame
with respect to the frame ![]() . The first three columns of
. The first three columns of ![]() contain the direction cosines of the axes of frame
contain the direction cosines of the axes of frame ![]() , whereas the fourth column represents the position of frame
, whereas the fourth column represents the position of frame ![]() .
.
In general, the displacement of joint ![]() is denoted as
is denoted as ![]() , where:
, where:
The position and orientation of link ![]() with respect to link
with respect to link ![]() is a function of
is a function of ![]() , that is,
, that is, ![]() .
.
The kinematic equation of a robotic arm gives the position and orientation of the last link with respect to the coordinate frame of the base, and obviously contains all generalized variables ![]() of the joints. Figure 10.3 shows pictorially the consecutive coordinate frames from the base up to the end-effector of the serial robotic kinematic chain.
of the joints. Figure 10.3 shows pictorially the consecutive coordinate frames from the base up to the end-effector of the serial robotic kinematic chain.
According to Eq. (2.18), the matrix ![]() given by:
given by:
![]() (10.2)
(10.2)
represents the position and orientation of the end-effector (which is the final link with respect to the base). It is now easy to determine ![]() for all types of robots (Figure 10.4) using Eq. (10.2).
for all types of robots (Figure 10.4) using Eq. (10.2).
10.2.2 Robot Inverse Kinematics
In the direct kinematics problem we are finding ![]() knowing the values of
knowing the values of ![]() . In the inverse kinematics problem we do the converse, that is, given
. In the inverse kinematics problem we do the converse, that is, given ![]() we determine
we determine ![]() by solving (10.2) with respect to
by solving (10.2) with respect to ![]() .
.
The direct kinematics Eq. (10.2) can be written in the vectorial form:
![]() (10.3)
(10.3)
where ![]() is the six-dimensional vector:
is the six-dimensional vector:
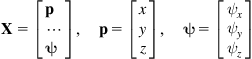 (10.4)
(10.4)
of the end-effector’s position ![]() and orientation
and orientation ![]() ,
, ![]() is a six-dimensional nonlinear column vectorial function, and
is a six-dimensional nonlinear column vectorial function, and
![]() (10.5)
(10.5)
Therefore, the inverse kinematics equation is:
![]() (10.6)
(10.6)
where ![]() denotes the usual inverse function of
denotes the usual inverse function of ![]() .
.
A straightforward practical method for inverting the kinematic Eq. (10.2) is the following. We start from:
![]()
and obtain the following sequence of equations:
 (10.7)
(10.7)
The elements of the left-hand sides of these equations are functions of the elements of ![]() and the first
and the first ![]() variables of the robot. The elements of the right-hand sides are constants or functions of the variables
variables of the robot. The elements of the right-hand sides are constants or functions of the variables ![]() . From each matrix equation we get 12 equations, that is, one equation for each of the elements of the four vectors
. From each matrix equation we get 12 equations, that is, one equation for each of the elements of the four vectors ![]() and
and ![]() . From these equations we can determine the values of
. From these equations we can determine the values of ![]() of the robot.
of the robot.
Although the solution of the direct kinematics problem is unique, it is not so for the inverse kinematics problem, because of the presence of trigonometric functions. In some cases, the solution can be found analytically, but, in general, the solution can only be found approximately using some approximate numerical method and the computer. Also, if the robot has more than six degrees of freedom (i.e., if we have a redundant robot), there are infinitely many solutions to ![]() that lead to the same position and orientation of the end-effector.
that lead to the same position and orientation of the end-effector.
10.2.3 Manipulability Measure
An important factor that determines the ease of arbitrarily changing the position and orientation of the end-effector by a manipulator is the so-called manipulability measure. Other factors are the size and geometric shape of the workspace envelope, the accuracy and repeatability, the reliability and safety, etc. Here, we will examine the manipulability measure, which was fully studied by Yoshikawa.
Given a manipulator with ![]() degrees of freedom, the direct kinematics equation is given by Eq. (10.3):
degrees of freedom, the direct kinematics equation is given by Eq. (10.3):
![]()
where ![]() is the m-dimensional vector
is the m-dimensional vector ![]() of the end-effector’s position
of the end-effector’s position ![]() and orientation vector
and orientation vector ![]() . Differentiating this relation we get the well-known differential kinematics model:
. Differentiating this relation we get the well-known differential kinematics model:
![]()
where ![]() is the manipulator’s Jacobian. This relation relates the velocity
is the manipulator’s Jacobian. This relation relates the velocity ![]() of the manipulator joints with the velocity of the end-effector, that is, the screw of the robot.
of the manipulator joints with the velocity of the end-effector, that is, the screw of the robot.
The set of all end-effector velocities that are realizable by joint velocities such as:
![]()
is an ellipsoid in the m-dimensional Euclidean space where ![]() is the dimensionality of
is the dimensionality of ![]() . The maximum speed of motion of the end-effector is along the major axis, and the minimum speed along the minor axis of this ellipsoid is called manipulability ellipsoid. One can show that the manipulability ellipsoid is the set of all
. The maximum speed of motion of the end-effector is along the major axis, and the minimum speed along the minor axis of this ellipsoid is called manipulability ellipsoid. One can show that the manipulability ellipsoid is the set of all ![]() that satisfy:
that satisfy:
![]()
for all ![]() in the range of
in the range of ![]() . Indeed, by using the relation
. Indeed, by using the relation ![]() (
(![]() =arbitrary constant vector) and the equality
=arbitrary constant vector) and the equality ![]() , we get
, we get
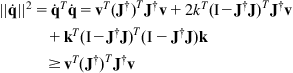
Thus, if ![]() , then
, then ![]() . Conversely, if we choose an arbitrary
. Conversely, if we choose an arbitrary ![]() such that
such that ![]() , then there exists a vector
, then there exists a vector ![]() such that
such that ![]() , that is,
, that is, ![]() . Then, we find that:
. Then, we find that:
![]()
![]()
In nonsingular configurations, the manipulability ellipsoid is given by:
![]()
The manipulability measure ![]() of the manipulator is defined as:
of the manipulator is defined as:
![]()
which for ![]() reduces to:
reduces to:
![]()
In this case, the set of all velocities that are implemented by a velocity ![]() of the joints such that:
of the joints such that:
![]()
is a parallelepiped in m-dimensional space with a volume of ![]() . This means that the measure
. This means that the measure ![]() is proportional to the volume of the parallelepiped, a fact that provides a physical representation of the manipulability measure.
is proportional to the volume of the parallelepiped, a fact that provides a physical representation of the manipulability measure.
10.2.4 The Two-Link Planar Robot
10.2.4.1 Kinematics
Consider the planar robot of Figure 10.5.
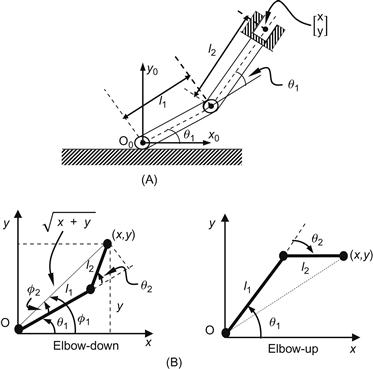
Figure 10.5 (A) Planar two degrees of freedom robot and (B) geometry for finding the inverse kinematic model (elbow-down, elbow-up).
The kinematic model of this robot can be found by simple trigonometric calculation. Referring to Figure 10.5 we readily obtain the direct kinematic model:
![]() (10.8a)
(10.8a)
that is:
![]() (10.8b)
(10.8b)
To derive the inverse kinematic model ![]() we work on Figure 10.5B.
we work on Figure 10.5B.
Thus, using the cosine rule we find:
![]()
from which the angle ![]() is found to be:
is found to be:
![]() (10.9a)
(10.9a)
The angle ![]() is equal to:
is equal to:
![]()
where:
![]()
Therefore:
![]() (10.9b)
(10.9b)
Actually, we have two configurations that lead to the same position ![]() of the end-effector, viz., elbow-down and elbow-up as shown in Figure 10.5. When
of the end-effector, viz., elbow-down and elbow-up as shown in Figure 10.5. When ![]() , that can be obtained if
, that can be obtained if ![]() , the ratio
, the ratio ![]() is not defined. If
is not defined. If ![]() , the base
, the base ![]() can be reached for all
can be reached for all ![]() . Finally, when a point is out of the workspace, the inverse kinematic problem has no solution.
. Finally, when a point is out of the workspace, the inverse kinematic problem has no solution.
The differential kinematics equation is:
![]()
Here, the Jacobian matrix ![]() is obtained by differentiating Eq. (10.8a), that is:
is obtained by differentiating Eq. (10.8a), that is:
![]() (10.10)
(10.10)
The inverse of ![]() is found to be:
is found to be:
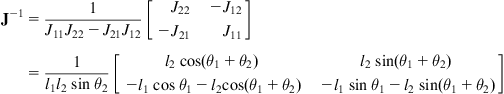 (10.11)
(10.11)
Thus, the inverse differential kinematics equation of the robot is:
![]() (10.12)
(10.12)
The singular (degenerate) configurations occur when ![]() , that is, when
, that is, when ![]() or
or ![]() . These two configurations correspond, respectively to the origin
. These two configurations correspond, respectively to the origin ![]() and to the full extension (i.e., when the robot end-effector is at the boundary of the workspace) (see Figure 10.5B).
and to the full extension (i.e., when the robot end-effector is at the boundary of the workspace) (see Figure 10.5B).
10.2.4.2 Dynamics
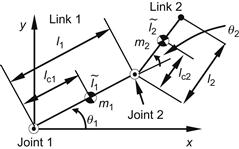
To derive the dynamic model of the robot we apply directly the Lagrange method. Consider the notation of Figure 10.6.
The symbols ![]() and
and ![]() have the usual meaning,
have the usual meaning, ![]() and
and ![]() are the masses of the two links (concentrated at their centers of gravity), and
are the masses of the two links (concentrated at their centers of gravity), and ![]() and
and ![]() are the lengths of the links. The symbol
are the lengths of the links. The symbol ![]() denotes the distance of the ith-link’s center of gravity (COG) from the axis of the joint
denotes the distance of the ith-link’s center of gravity (COG) from the axis of the joint ![]() , and
, and ![]() denotes the moment of inertia of link
denotes the moment of inertia of link ![]() with respect to the axis passing via the COG of this link and is perpendicular to the plane
with respect to the axis passing via the COG of this link and is perpendicular to the plane ![]() (parallel to the axis
(parallel to the axis ![]() ). Here,
). Here, ![]() and
and ![]() , and the kinematic and potential energies of the links 1 and 2 are given by:
, and the kinematic and potential energies of the links 1 and 2 are given by:
![]() (10.13a)
(10.13a)
![]() (10.13b)
(10.13b)
where ![]() is the position vector of the COG of link 2 with:
is the position vector of the COG of link 2 with:
![]()
and ![]() .
.
Using the Lagrangian function of the robot, ![]() , we find the equations:1
, we find the equations:1
![]() (10.14)
(10.14)
with:
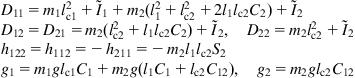 (10.15)
(10.15)
where ![]() and
and ![]() are the external torques applied to joints 1 and 2. The coefficient
are the external torques applied to joints 1 and 2. The coefficient ![]() is the effective inertia of the joint
is the effective inertia of the joint ![]() ,
, ![]() is the coupling inertia of joints
is the coupling inertia of joints ![]() and
and ![]() ,
, ![]() is the coefficient of centrifugal force,
is the coefficient of centrifugal force, ![]() is the coefficient of Coriolis acceleration of the joint
is the coefficient of Coriolis acceleration of the joint ![]() due to the velocities of the joints
due to the velocities of the joints ![]() and
and ![]() , and
, and ![]() represent the torques due to gravity. The dynamic relations in Eqs. (10.14) and (10.15) can be written in the standard compact form:
represent the torques due to gravity. The dynamic relations in Eqs. (10.14) and (10.15) can be written in the standard compact form:
![]() (10.16a)
(10.16a)
![]() (10.16b)
(10.16b)
 (10.16c)
(10.16c)
where ![]() denotes a column vector with elements
denotes a column vector with elements ![]() . In the special case, where the link masses
. In the special case, where the link masses ![]() and
and ![]() are assumed to be concentrated at the end of each link, we have
are assumed to be concentrated at the end of each link, we have ![]() and
and ![]() . It is easy to verify the properties described by Eqs. (3.12) and (3.13) and the antisymmetricity of
. It is easy to verify the properties described by Eqs. (3.12) and (3.13) and the antisymmetricity of ![]() , where
, where ![]() is the total kinetic energy
is the total kinetic energy ![]() of the robot.
of the robot.
10.2.4.3 Manipulability Measure
If we use the position ![]() of the end-effector as the vector
of the end-effector as the vector ![]() , then (see (10.10)):
, then (see (10.10)):
![]()
and so the manipulability measure ![]() is:
is:
![]()
Thus, the optimal configurations of the manipulator, at which ![]() is maximum, are:
is maximum, are: ![]() for any
for any ![]() and
and ![]() . If the lengths
. If the lengths ![]() and
and ![]() are specified under the condition of constant total length (i.e.,
are specified under the condition of constant total length (i.e., ![]() ), then the manipulability measure takes its maximum when
), then the manipulability measure takes its maximum when ![]() for any
for any ![]() and
and ![]() .
.
10.3 MM Modeling
The total kinematic and dynamic models of an MM are complex and strongly coupled, combining the models of the mobile platform and the fixed robotic manipulator [1,3,7]. Today, MMs are in use with differential-drive, tricycle, car-like, and omnidirectional platforms that offer maximum maneuverability.
10.3.1 General Kinematic Model
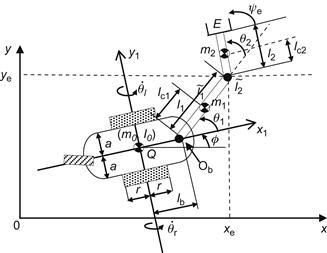
Consider the MM of Figure 10.7 which has a differential-drive platform and a multilink robotic manipulator.
Here, we have the following four coordinate frames:
![]() is the world coordinate frame,
is the world coordinate frame,
![]() is the platform coordinate frame,
is the platform coordinate frame,
Then, the manipulator’s end-effector position/orientation with respect to ![]() is given by (see Eq. (10.2)):
is given by (see Eq. (10.2)):
![]() (10.17)
(10.17)
In vectorial form, the end-effector position/orientation vector ![]() in world coordinates has the form:
in world coordinates has the form:
![]() (10.18)
(10.18)
where:
![]()
![]()
![]()
Therefore, differentiating Eq. (10.18) with respect to time we get:
![]() (10.19)
(10.19)
where ![]() is given by the kinematic model of the platform (see (6.1)):
is given by the kinematic model of the platform (see (6.1)):
![]() (10.20a)
(10.20a)
and ![]() by the manipulator’s kinematic model. Assuming that the manipulator is constraint-free, we can write:
by the manipulator’s kinematic model. Assuming that the manipulator is constraint-free, we can write:
![]() (10.20b)
(10.20b)
where ![]() is the vector of manipulator’s joint commands. Combining Eqs. (10.19), (10.20a), and (10.20b) we get the overall kinematic model of the MM:
is the vector of manipulator’s joint commands. Combining Eqs. (10.19), (10.20a), and (10.20b) we get the overall kinematic model of the MM:
 (10.21a)
(10.21a)
where:
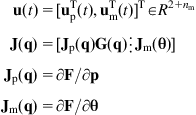 (10.21b)
(10.21b)
Equation (10.21a) represents the total kinematic model of the MM from the inputs to the end-effector (task) variables.
Actually, in the present case the system is subject to the nonholonomic constraint:
![]() (10.22)
(10.22)
where ![]() cannot be eliminated by integration. Therefore,
cannot be eliminated by integration. Therefore, ![]() should involve a row representing this constraint. Since the dimensionality
should involve a row representing this constraint. Since the dimensionality ![]() of the control input vector
of the control input vector ![]() is less than the total number
is less than the total number ![]() of variables (degrees of freedom) to be controlled, the system is always underactuted.
of variables (degrees of freedom) to be controlled, the system is always underactuted.
10.3.2 General Dynamic Model
The Lagrange dynamic model of the MM is given by Eq. (3.16):
![]() (10.23)
(10.23)
where ![]() is given by Eq. (10.22). This model contains two parts, namely:
is given by Eq. (10.22). This model contains two parts, namely:
Platform Part
![]()
Manipulator Part
![]()
where the index ![]() refers to the platform and
refers to the platform and ![]() to the manipulator, and the symbols have the standard meaning. Appling the technique of Section 3.2.4 we eliminate the nonholonomic constraint
to the manipulator, and the symbols have the standard meaning. Appling the technique of Section 3.2.4 we eliminate the nonholonomic constraint ![]() , and get the reduced (unconstrained) model of the form of Eqs. (3.19a) and (3.19b):
, and get the reduced (unconstrained) model of the form of Eqs. (3.19a) and (3.19b):
![]() (10.24)
(10.24)
where:
![]()
and ![]() , and
, and ![]() are given by the combination of the respective terms in the platform and manipulator parts (the details of derivation are straightforward and are left as exercise).
are given by the combination of the respective terms in the platform and manipulator parts (the details of derivation are straightforward and are left as exercise).
10.3.3 Modeling a Five Degrees of Freedom Nonholonomic MM
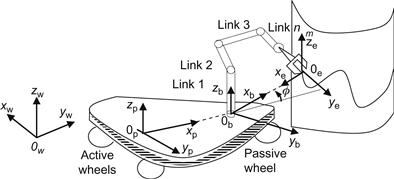
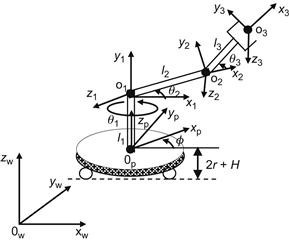
Here, the above general methodology will be applied to the MM of Figure 10.8 which consists of a differential-drive mobile platform and a two-link planar manipulator [3,22].
10.3.3.1 Kinematics
Without loss of generality, the COG ![]() is assumed to coincide with the rotation point
is assumed to coincide with the rotation point ![]() (midpoint of the two wheels), that is,
(midpoint of the two wheels), that is, ![]() . The nonholonomic constraint of the platform is:
. The nonholonomic constraint of the platform is:
![]()
This constraint, when expressed at the base ![]() of the manipulator, becomes:
of the manipulator, becomes:
![]()
where ![]() is the distance between the points
is the distance between the points ![]() and
and ![]() . The kinematic equations of the wheeled mobile robot (WMR) platform (at the point
. The kinematic equations of the wheeled mobile robot (WMR) platform (at the point ![]() ) are:
) are:
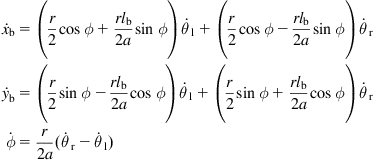 (10.25)
(10.25)
which are written in the Jacobian form:
![]()
where:
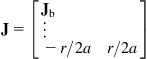
 (10.26)
(10.26)
![]() (10.27)
(10.27)
The kinematic parameters of the two-link manipulator are those of Figure 10.6, where now its first joint has linear velocity ![]() . The linear velocity
. The linear velocity ![]() of the end-effector is given by:
of the end-effector is given by:
![]() (10.28a)
(10.28a)
where ![]() :
:
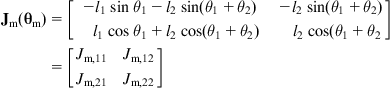 (10.28b)
(10.28b)
is the Jacobian matrix of the manipulator with respect to its base coordinate frame (see Eq. (10.10)). Here, ![]() is given by the third part of Eq. (10.25), that is,
is given by the third part of Eq. (10.25), that is, ![]() . Thus:
. Thus:
![]() (10.29a)
(10.29a)
and so:
![]() (10.29b)
(10.29b)
The overall kinematic equation of the MM is:
![]() (10.30a)
(10.30a)
where:
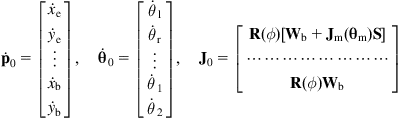 (10.30b)
(10.30b)
If the mobile platform of the MM is of the tricycle or car-like type shown in Figure 2.8 or Figure 2.9, its position/orientation is described by four variables ![]() and
and ![]() , and the kinematic Eq. (2.45) or Eq. (2.53) is enhanced as in Eq. (10.25) with the
, and the kinematic Eq. (2.45) or Eq. (2.53) is enhanced as in Eq. (10.25) with the ![]() terms. The overall kinematic model of the MM is found by the same procedure.
terms. The overall kinematic model of the MM is found by the same procedure.
10.3.3.2 Dynamics
Assuming that the moment of inertia of the passive wheel is negligible, the Lagrangian of the MM is found to be:
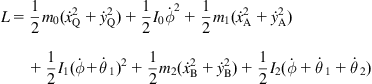 (10.31)
(10.31)
![]() are mass and moment of inertia of the platform,
are mass and moment of inertia of the platform,
![]() are masses and moments of inertia of links 1 and 2, respectively,
are masses and moments of inertia of links 1 and 2, respectively,
Using the Lagrangian (10.31) we derive the dynamic model of Eq. (10.23), with the nonholonomic constraint:
![]() (10.32)
(10.32)
Now, using the transformation ![]() with
with ![]() , where:
, where:
![]()
and ![]() is selected as:
is selected as:
 (10.33)
(10.33)
where ![]() is the
is the ![]() unit matrix, and
unit matrix, and
 (10.34)
(10.34)
the constrained Lagrangian model is reduced, as usual, to the unconstrained form (10.24).
10.3.4 Modeling an Omnidirectional MM
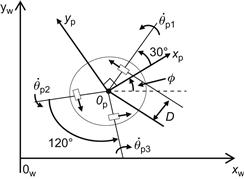
Here, the kinematic and dynamic model of the MM shown in Figure 10.9 will be derived. This MM involves a three-wheel omnidirectional platform (with orthogonal wheels) and a 3D manipulator [8,11].
10.3.4.1 Kinematics
As usual, the kinematic model of the MM is found by combining the kinematic models of the platform and the manipulator.
The workspace of the robot is described by the world coordinate frame ![]() . The platform’s coordinate frame
. The platform’s coordinate frame ![]() has its origin at the COG of the platform, and the wheels have a radius
has its origin at the COG of the platform, and the wheels have a radius ![]() , an angle
, an angle ![]() between them, and a distance D from the platform’s COG. The kinematic model of the robot was derived in Section 2.4. For the platform shown in Figure 10.9, the model given by Eqs. (2.74a) and (2.74b) becomes:
between them, and a distance D from the platform’s COG. The kinematic model of the robot was derived in Section 2.4. For the platform shown in Figure 10.9, the model given by Eqs. (2.74a) and (2.74b) becomes:
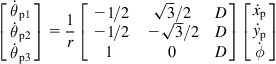
that is,
![]() (10.35)
(10.35)
where ![]() are the angular velocities of the wheels,
are the angular velocities of the wheels, ![]() the rotational angle between
the rotational angle between ![]() and
and ![]() axes, and
axes, and ![]() are the components of the platform’s velocity expressed in the platform’s (moving) coordinate system. The coordinate transformation matrix between the world and the platform coordinate frames is:
are the components of the platform’s velocity expressed in the platform’s (moving) coordinate system. The coordinate transformation matrix between the world and the platform coordinate frames is:
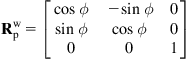 (10.36)
(10.36)
Thus, the relation between ![]() and
and ![]() is
is
![]() (10.37)
(10.37)
Inverting Eq. (10.37) we get the direct differential kinematic model of the robot from ![]() to
to ![]() as:
as:
![]() (10.38a)
(10.38a)
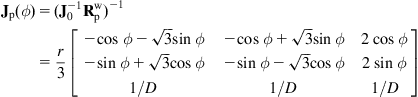 (10.38b)
(10.38b)
Now, the platform’s kinematic model of Eq. (10.38a) will be integrated with the manipulator’s kinematic model (see Figure 10.10).
From Figure 10.9 we get:
 (10.39)
(10.39)
where ![]() is the height of the platform. Now, differentiating Eq. (10.39) and using Eqs. (10.38a) and (10.38b) we get:
is the height of the platform. Now, differentiating Eq. (10.39) and using Eqs. (10.38a) and (10.38b) we get:
![]() (10.40)
(10.40)
where: ![]() and
and ![]() is a
is a ![]() matrix with columns:
matrix with columns:
 (10.41)
(10.41)
The notations used in the above expressions are:
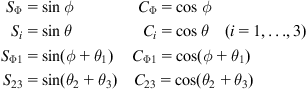
10.3.4.2 Dynamics
To find the dynamic model of the MM, the local coordinate frames are employed according to the Denavit–Hartenberg convention. Figure 10.10 shows all the coordinate frames involved. Using the above notations, we obtain the following rotational matrices:
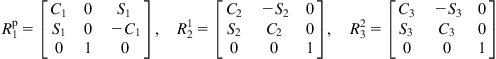

Now, for each rigid body composing the MM, the kinetic and potential energies are found. Then the Lagrangian function ![]() is built. Finally, the equations of the generalized forces are calculated using the Lagrangian function:
is built. Finally, the equations of the generalized forces are calculated using the Lagrangian function:
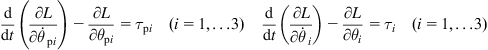
where ![]() are the generalized torques for the wheel actuators that drive the platform, and
are the generalized torques for the wheel actuators that drive the platform, and ![]() are the generalized torques for the joint actuators that drive the links of the manipulator. The parameters of the MM are defined in Table 10.1:
are the generalized torques for the joint actuators that drive the links of the manipulator. The parameters of the MM are defined in Table 10.1:
Then, the differential equations of the dynamic model are expressed in compact form as:
![]() (10.42)
(10.42)
where:
![]()

 (10.43)
(10.43)
with ![]() and
and ![]() being defined via intermediate coefficients [8].
being defined via intermediate coefficients [8].
10.4 Control of MMs
10.4.1 Computed-Torque Control of Differential-Drive MM
Here, the control of the five degrees of freedom MM studied in Section 10.3.3 will be considered [22]. We use the reduced dynamic model of Eq. (10.24) with parameters given by Eqs. (10.32)–(10.34). The vector ![]() of generalized variables is:
of generalized variables is:
![]() (10.44a)
(10.44a)
and the vector ![]() is:
is:
![]() (10.44b)
(10.44b)
To convert ![]() to the Cartesian coordinates velocity vector:
to the Cartesian coordinates velocity vector:
![]() (10.44c)
(10.44c)
we use the Jacobian relation (10.30a) and (10.30b).
![]() (10.44d)
(10.44d)
where the ![]() Jacobian matrix
Jacobian matrix ![]() is invertible. Differentiating Eq. (10.44d) we get:
is invertible. Differentiating Eq. (10.44d) we get:
![]()
which, if solved for ![]() , gives:
, gives:
![]() (10.45)
(10.45)
Now, introducing Eq. (10.45) into Eq. (10.24), and premultiplying by ![]() gives the model:
gives the model:
![]() (10.46)
(10.46)
where:
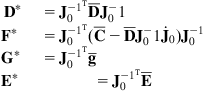 (10.47)
(10.47)
If the desired path for ![]() is
is ![]() , and the error is defined as
, and the error is defined as ![]() , we select as usual the computed-torque law:
, we select as usual the computed-torque law:
![]() (10.48)
(10.48)
Introducing Eq. (10.48) into Eq. (10.46), under the assumption that the robot parameters are precisely known, gives:
![]() (10.49a)
(10.49a)
Now, we can use the linear feedback control law:
![]() (10.49b)
(10.49b)
In this case, the dynamics of the closed-loop error system is described by:
![]()
Therefore, selecting properly ![]() and
and ![]() we can get the desired performance specifications.
we can get the desired performance specifications.
10.4.2 Sliding-Mode Control of Omnidirectional MM
We work with the dynamic model of the MM, given by Eq. (10.42) which due to the omnidirectionality of the platform does not involve any nonholonomic constraint [8,11]. Applying computed-torque control:
![]() (10.50a)
(10.50a)
we arrive, as usual, to the linear dynamic system:
![]() (10.50b)
(10.50b)
![]() (10.50c)
(10.50c)
that leads to an asymptotically stable error dynamics.
If ![]() and
and ![]() are subject to uncertainties, and we know only their approximations
are subject to uncertainties, and we know only their approximations ![]() , then the computed-torque controller is:
, then the computed-torque controller is:
![]() (10.51a)
(10.51a)
and the system dynamics is given by:
![]() (10.51b)
(10.51b)
In this case, some appropriate robust control technique must be used. A convenient controller is the sliding-mode controller described in Section 7.2.2. This controller involves a nominal term (based on the computed-torque control law), and an additional term that faces the imprecision of the dynamic model.
The sliding condition for a multiple-input multiple-output system is a generalization of Eq. (7.14):
![]() (10.52a)
(10.52a)
with:
![]() (10.52b)
(10.52b)
where ![]() and
and ![]() is a Hurwitz (stable) matrix. The condition (10.52a) guarantees that the trajectories point towards the surface
is a Hurwitz (stable) matrix. The condition (10.52a) guarantees that the trajectories point towards the surface ![]() for all
for all ![]() . This can be shown by choosing a Lyapunov function of the form:
. This can be shown by choosing a Lyapunov function of the form:
![]()
where ![]() is the inertia matrix of the MM. Differentiating
is the inertia matrix of the MM. Differentiating ![]() we get:
we get:
![]() (10.53a)
(10.53a)
The control law is now defined as:
![]() (10.53b)
(10.53b)
where ![]() is a vector with components
is a vector with components ![]() . Furthermore, the
. Furthermore, the ![]() term is the control law part which could make
term is the control law part which could make ![]() , if there is no dynamic imprecision inside the estimated dynamic model, that is, according to Eq. (10.53a):
, if there is no dynamic imprecision inside the estimated dynamic model, that is, according to Eq. (10.53a):
![]()
where ![]() and
and ![]() are the available estimates of
are the available estimates of ![]() and
and ![]() . Now, calling
. Now, calling ![]() and
and ![]() the real matrices of the robot, we define the matrices:
the real matrices of the robot, we define the matrices:
![]()
as the bounds on the modeling errors. Then, it is possible to choose the components ![]() of the vector
of the vector ![]() such that:
such that:
![]() (10.54a)
(10.54a)
If this control mode is used, the condition:
![]() (10.54b)
(10.54b)
is verified to hold. This means that the sliding surface ![]() is reached in a finite time, and that once on the surface, the trajectories remain on the surface and, therefore, tend to
is reached in a finite time, and that once on the surface, the trajectories remain on the surface and, therefore, tend to ![]() exponentially.
exponentially.
10.5 Vision-Based Control of MMs
10.5.1 General Issues
As described in Section 9.4, the image-based visual control uses the image Jacobian (or interaction) matrix. Actually, the inverse or generalized inverse of the Jacobian matrix or its generalized transpose is used, in order to determine the screw (or velocity twist) ![]() of the end-effector which assures the achievement of a desired task. In MMs where the platform is omnidirectional (and does not involve any nonholonomic constraint), the method discussed in Section 9.4 is directly applicable. However, if the MM platform is nonholonomic, special care is required for both determining and using the corresponding image Jacobian matrix. This can be done by combining the results of Sections 9.2, 9.4, and 10.3.
of the end-effector which assures the achievement of a desired task. In MMs where the platform is omnidirectional (and does not involve any nonholonomic constraint), the method discussed in Section 9.4 is directly applicable. However, if the MM platform is nonholonomic, special care is required for both determining and using the corresponding image Jacobian matrix. This can be done by combining the results of Sections 9.2, 9.4, and 10.3.
The Jacobian matrix is defined by Eq. (9.11) and relates the end-effector screw:
![]() (10.56a)
(10.56a)
with the feature vector rate of change:
![]() (10.56b)
(10.56b)
that is:
![]() (10.56c)
(10.56c)
The relation of ![]() to
to ![]() , where
, where ![]() is the position vector
is the position vector ![]() rigidly attached to the end-effector, is given by Eq. (9.4a):
rigidly attached to the end-effector, is given by Eq. (9.4a):
![]() (10.57)
(10.57)
where ![]() is the skew symmetric matrix of Eq. (9.4b). The matrix
is the skew symmetric matrix of Eq. (9.4b). The matrix ![]() is the robot Jacobian part. The relation of
is the robot Jacobian part. The relation of ![]() to
to ![]() is given by Eq. (9.13a):
is given by Eq. (9.13a):
![]() (10.58a)
(10.58a)
where:
![]() (10.58b)
(10.58b)
The matrix ![]() is the camera interaction part. Combining Eqs. (10.57) and (10.58a) we get the expression of
is the camera interaction part. Combining Eqs. (10.57) and (10.58a) we get the expression of ![]() , namely,
, namely,
![]() (10.59)
(10.59)
as given in Eq. (9.15) for the case of two image plane features ![]() and
and ![]() .
.
Now, we will examine the case where the task features are the components of the vector:
![]()
In this case, the camera interaction part ![]() , in Eq. (10.58b), is given by:
, in Eq. (10.58b), is given by:
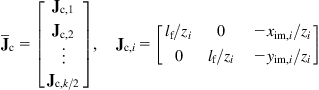 (10.60a)
(10.60a)
for ![]() . Therefore, the overall Jacobian matrix
. Therefore, the overall Jacobian matrix ![]() is given by:
is given by:
 (10.60b)
(10.60b)
The control of the MM needs the control of the platform and the manipulator mounted on it. Two ways to do this are the following:
1. Control the platform and the arm separately, and then treat the existing coupling between them.
2. Control the platform and the arm jointly with the coupling kinematics and dynamics included in the overall model used (full-state model).
10.5.2 Full-State MM Visual Control
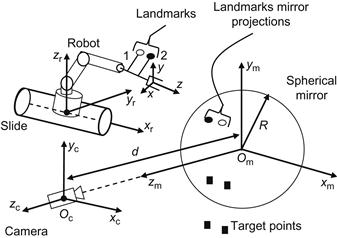
The vision-based control of mobile platforms was studied in Section 9.5, where several representative problems (pose stabilizing control, wall following control, etc.) were considered. Here we will consider the pose stabilizing control of MMs combining the platform pose and manipulator/camera pose control [3,14]. Actually, the results of Section 9.5.1 concern the case of stabilizing the platform’s pose ![]() and the camera’s pose
and the camera’s pose ![]() . The camera pose control can be regarded as the stabilizing pose control of a one-link manipulator (using the notation
. The camera pose control can be regarded as the stabilizing pose control of a one-link manipulator (using the notation ![]() ). Therefore, the vision-based control of a general MM can be derived by direct extension of the controller derived in Section 9.5.1. This controller is given by Eqs. (9.49a), (9.49b), (9.50a), and (9.50b), and stabilizes to zero the total pose vector:
). Therefore, the vision-based control of a general MM can be derived by direct extension of the controller derived in Section 9.5.1. This controller is given by Eqs. (9.49a), (9.49b), (9.50a), and (9.50b), and stabilizes to zero the total pose vector:
![]()
on the basis of feature measurements:
![]()
of three nonaligned target feature points ![]() and
and ![]() , provided by an onboard camera, and a sensor measuring
, provided by an onboard camera, and a sensor measuring ![]() (see Figure 9.4). This controller employs the image Jacobian relation (9.25a) and (9.25b):
(see Figure 9.4). This controller employs the image Jacobian relation (9.25a) and (9.25b):
![]()
where ![]() and
and ![]() are given by Eqs. (9.21) and (9.24b), respectively.
are given by Eqs. (9.21) and (9.24b), respectively.
Using three feature points as in Figure 9.4, the camera part ![]() of the Jacobian
of the Jacobian ![]() has the same form as in Eq. (9.21). But the robot part
has the same form as in Eq. (9.21). But the robot part ![]() of the image Jacobian is different depending on the number and type of the manipulator links.
of the image Jacobian is different depending on the number and type of the manipulator links.
For example, if we consider the five-link MM of Figure 10.8, the Jacobian matrix of the overall system (including the coupling between the platform and the manipulator) is given by Eqs. (10.30a) and (10.30b), where the wheel motor velocities ![]() and
and ![]() are equivalently used as controls instead of
are equivalently used as controls instead of ![]() and
and ![]() . Now, the controller design proceeds in the usual way as described in Sections 9.3 and 9.4 for both cases of position-based and image-based control.
. Now, the controller design proceeds in the usual way as described in Sections 9.3 and 9.4 for both cases of position-based and image-based control.
References
1. Padois V, Fourquet JY, Chiron P. Kinematic and dynamic model-based control of wheeled mobile manipulators: a unified framework for reactive approaches. Robotica. 2007;25(2):157–173.
2. Seelinger M, Yoder JD, Baumgartner ET, Skaar BR. High-precision visual control of mobile manipulators. IEEE Trans Robot Autom. 2002;18(6):957–965.
3. Tzafestas CS, Tzafestas SG. Full-state modeling, motion planning and control of mobile manipulators. Stud Inform Control. 2001;10(2):109–127.
4. Kumara P, Abeygunawardhana W, Murakami T. Control of two-wheel mobile manipulator on a rough terrain using reaction torque observer feedback. J Autom Mobile Robot Intell Syst. 2010;4(1):56–67.
5. Chung JH, Velinsky SA. Robust interaction control of a mobile manipulator: dynamic model based coordination. J Intell Robot Syst. 1999;26(1):47–63.
6. Li Z, Chen W, Liu H. Robust control of wheeled mobile manipulators using hybrid joints. Int J Adv Rob Syst. 2008;5(1):83–90.
7. Yamamoto Y, Yun X. Effect of the dynamic interaction on coordinated control of mobile manipulators. IEEE Trans Rob Autom. 1996;12(5):816–824.
8. Tzafestas SG, Melfi A, Krikochoritis T. Omnidirectional mobile manipulator modeling and control: analysis and simulation. Syst Anal Model Control. 2001;40:329–364.
9. Mazur A, Szakiel D. On path following control of non-holonomic mobile manipulators. Int J Appl Math Comput Sci. 2009;19(4):561–574.
10. Meghadari A, Durali M, Naderi D. Investigating dynamic interaction between one d.o.f manipulator and vehicle of a mobile manipulator. J Intell Robot Syst. 2000;28:277–290.
11. Watanabe K, Sato K, Izumi K, Kunitake Y. Analysis and control for an omnidirectional mobile manipulator. J Intell Robot Syst. 2000;27(1–2):3–20.
12. De Luca A, Oriolo G, Giordano PR. Image-based visual servoing schemes for nonholonomic mobile manipulators. Robotica. 2007;25:131–145.
13. Burshka D, Hager G. Vision-based control of mobile robots. In: Proceedings of 2001 IEEE international conference robotics and automation. Seoul, Korea; May 21–26, 2001.
14. Tsakiris D, Samson C, Rives P. Vision-based time-varying stabilization of a mobile manipulator. In: Proceedings of fourth international conference on control, automation, robotics and vision (ICARCV’96). Westin Stanford, Singapore; December 3–6, 1996. p. 1–5.
15. Yu Q, Chen Ming I. A general approach to the dynamics of nonholonomic mobile manipulator systems. Trans ASME. 2002;124:512–521.
16. DeLuca A, Oriolo G, Giordano PR. Kinematic control of nonholonomic mobile manipulators in the presence of steering wheels. In: Proceedings of 2010 IEEE international conference on robotics and automation. Anchorage, AK; May 3–8, 2010. p. 1792–98.
17. Phuoc LM, Martinet P, Kim H, Lee S. Motion planning for nonholonomic mobile manipulator based visual servo under large platform movement errors at low velocity. In: Proceedings of 17th IFAC world congress. Seoul, Korea; July 6–11, 2008. p. 4312–17.
18. Gilioli M, Melchiori C. Coordinated mobile manipulator point-stabilization using visual-servoing techniques. In: Proceedings of IEEE/RSJ international conference on intelligent robots and systems. Lausanne, CH; 2002. p. 305–10.
19. Ma Y, Kosecha J, Sastry S. Vision guided navigation for nonholonomic mobile robot. IEEE Trans Robot Autom. 1999;15(3):521–536.
20. Zhang Y. Visual servoing of a 5-DOF mobile manipulator using an omnidirectional vision system. Technical Report RML-3-2, University of Regina, 2006.
21. Bayle B, Fourquet JY, Renaud M. Manipulability analysis for mobile manipulators. In: Proceedings of 2001 IEEE international conference on robotics and automation. Seoul, Korea; May 21–26, 2001. p. 1251–56.
22. Papadopoulos E, Poulakakis J. Trajectory planning and control for mobile manipulator systems. In: Proceedings of eighth IEEE Mediterranean conference on control and automation. Patras, Greece; July 17–19, 2000.
23. Yamamoto Y, Yun X. Coordinating locomotion and manipulation of a mobile manipulator. In: Proceedings of 31st IEEE conference on decision and control. Tucson, AZ; December, 1992. p. 2643–48.
24. Yamamoto Y, Yun X. Modeling and compensation of the dynamic interaction of a mobile manipulator. In: Proceedings of IEEE conference on robotics and automation. San Diego, CA; May 8–13, 1994. p. 2187–92.
25. Zhang Y, Mehrandezh M. Visual servoing of a 5-DOF mobile manipulator using a panoramic vision system. In: Proceedings of 2007 Canadian conference on electrical and computer engineering. Vancouver, BC, Canada; April 22–26, 2007. p. 453–56.
26. Zhang Y, Mehrandezh M. Visual servoing of a 5-DOF mobile manipulator using a catadioptric vision system. In: Proceedings of SPIE, the international society for optical engineering; 2007. p. 6–17.
27. Zhang Y. Visual servoing of a 5-DOF mobile manipulator using panoramic vision system [M.Sc. thesis]. Regina, Canada, Faculty of Engineering, University of Regina, 2007.
1If there is friction ![]() in the motors of the joints (e.g.,
in the motors of the joints (e.g., ![]() friction coefficient), then
friction coefficient), then ![]() should be replaced by
should be replaced by ![]() .
.