Chapter 5

First-Order Logic (FOL) or Predicate Logic (PL1, PC1)

In Aristotle’s syllogistic, every statement consists of the attribution of a property to an object, which means that they are expressed using unary predicates and therefore formalized using PL. This is no longer sufficient when we need to consider relations (binary, ternary, etc.) between objects. These relations cannot be reduced to unary relations (properties)¹.

Handling properties and relations is of course essential in programming (logic programming, multi-agent programming, etc.)².

If we believe we can manage using formalizations, such as those after definition 2.8, how can we talk about objects that have properties P,Q,… or that are related to other objects?

For example, how can we use PL to verify that the following reasoning is correct:

All horses are animals.

Some horses are white.

Therefore, some white horses are animals.

Similarly, how can the following reasoning, which should obviously be correct, be translated into PL?

For all x, xRa, therefore there exists an x such that aRx

If we denote by P: For all x, xRa

and:

Q: there exists x such that aRx

this reasoning would be classified as incorrect (P can be evaluated to true and Q to false).

This reasoning can be formalized as follows: (as you already know, see also definition 5.1).

and now “we can see” that it is correct.

The soundness of these reasonings is based on the relation between “for all” (or “all”) and “there exists” (or “some”).

Another very familiar example is that of transitivity: for any objects named x, y, and 2, if x is related to y and y is related to z then x is related to z. Obviously, these sentences cannot be expressed in PL in order to be used in a reasoning. They could be denoted by P (or Q,…), but that would not be very useful.

One last example: how can the following sentence be translated in PL?

The object named 0 satisfies property P, and if an object x satisfies P, then the successor of x also satisfies P…

It is worth mentioning that in finite universes, it is possible to stay within PL. For example, the argumentation if all men are mortal and a given object satisfies the property of being a man, then this object is mortal (see also example 5.9) could be specified with the following propositional schema in a universe with n men:

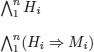
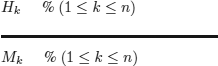
where the prepositional symbols H_i and M_i, respectively, denote i is a man and i is mortal.

This way of proceeding is not very natural, it is theoretically limited to finite universes and practically limited by the size of these universes; more importantly, it prevents the usage of variables (because all cases have to be enumerated).

We are currently talking about the limits of the expressive power of a language (and how they can be overcome). As can be expected, once more things can be expressed, there is a risk of not being able to answer all questions on wffs of this language with more expressive power.

In computer science, it is well-known that if we use a language that forbids some control structures, then the halting problem becomes decidable for programs written in this language.

From the point of view of decidability: the fragment of FOL called monadic logic is decidable (see section 5.8). As soon as predicates with an arity greater than or equal to 2 are allowed, we obtain undecidable fragments.

REMARK 5.1.- The language of FOL was introduced by G. Frege in 1879, but the notations that are currently used are similar to those introduced by Peano in 1889. Formal systems were introduced by Hilbert and Ackermann in 1928 (see also remark 5.21).

5.1. Syntax

DEFINITION 5.1.- (FOL language). Consider a signature , where:

is a set of variables;

is a set of function symbols, n_i: arity (n_i ≥ 0).

Function symbols of arity 0 are constants, and the set of constants is denoted by ( ⊆ );

set of predicate symbols, k_i: arity (k_i ≥ 1);

The language (i.e. the set of wffs) of FOL, denoted by , is the smallest set such that:

– if (see definition 4.1), then: is an atomic formula;

– a literal is an atomic formula or its negation;

– if and and , then:

(we will also write );

– are called the universal quantifier and existential quantifier, respectively, and x is the quantified variable. A variable will not be quantified more than once (that would make no sense);

– in , is the scope of the quantifiers.;

– the set is the set of logical symbols or logical constants;

– the set is the set of non-logical symbols corresponding to the considered theory;

– if the signature does not contain any functional symbol of arity or the predicate symbol =, then we have pure FOL;

– a wff can be viewed as a string (or word) on vocabulary Ω (i.e. a finite sequence of symbols in Ω). A subformula of a wff is a substring³ of (considered as a string), which is also a wff;

– a wff is in nnf if it is constructed with literals, the connectives ∧ and ∨, and the quantifiers ∀ and ∃⁴. Every wff can be transformed into another one that is equivalent and in nnf.

REMARK 5.2.– (the set of wffs of FOL is denumerably infinite). As the set of variables is denumerably infinite, the set of logical symbols finite and the set of non-logical symbols denumerably infinite, it is simple to design an algorithm that enumerates all the wffs using the rules of definition 5.1.

Every infinite set of wffs of FOL will therefore be denumerably infinite (as it will be the subset of a denumerably infinite set).

DIGRESSION 5.1.– In discrete mathematics, researchers use the terminology Boolean predicates or constraints on Boolean variables.

The arity is the number of variables that occur in the constraints.

DIGRESSION 5.2.– (variables 2)⁵. It is interesting to have a historical recollection here on mathematical notations and, in particular, on the notion of a variable.

Letters were used in Antiquity to denote points, lines, etc. in a generic way, meaning that letters were used as names.

In arithmetic, symbolic abbreviations are very ancient, they were already used by Egyptians.

Diophantus (circa 3rd Century) introduced a particular symbol for the unknowns in algebra, and this seems to be the very first appearance of what would become a numerical variable in mathematics.

It is acknowledged that the first symbolic algebraic language is due to François Viète (1540-1603). Viète used letters to represent unknowns, powers of the unknowns and undetermined coefficients (generic names).

Descartes, Newton, Leibniz, Euler, etc. changed and modified the language introduced by Viète.

In mathematical logic, the concept of a variable was explicitly used by G. Frege.

DEFINITION 5.2.– (free and bound variables). The occurrence of a variable x in a wff of is bound iff x appears immediately after a quantifier, or if x is in the scope of a quantifier (and has the same name as the quantified variable). Every other occurrence is free.

Below, and denote wffs of .

Set of free variables in a formula:

Free_vars (see definition4.2)

Free_vars = Free_vars

Free_vars = Free_vars = Free_vars = Free_vars = Free_vars Free_vars

Free_vars = Free_vars = Free_vars

Set of bound variables in a formula:

Bound_vars

Bound_vars = Bound_vars

Bound_vars = Bound_vars = Bound_vars = Bound_vars = Bound_vars Bound_vars

Bound_vars = Bound_vars = Bound_vars

REMARK 5.3.– The same variable may have free and bound occurrences in a formula, for example, in formula

The first occurrence of x is free, the second and third are bound.

The first and second occurrences of y are bound, the third is free.

DEFINITION 5.3.– (closed and open formulas). A wff is closed, written closed wff (cwff) iff it does not contain any free variable. Otherwise, it is open and written open wff(owff).

REMARK 5.4.– A bound variable is a variable such that the wff it appears in has a meaning that is independent of this variable. For example, in:

x is bound and y is free.

In programming languages, local variables are bound, global variables are free.

See remark 5.9 on the conceptual difference between a cwff and an owff.

EXAMPLE 5.1.– (translation into FOL). Consider the statement:

Someone who loves all animals loves all men

that we restate as a reasoning, by formulating all the implicit knowledge. There are two “natural” translations, depending on whether “someone” is translated into:

i) animal (not necessarily human) or

ii) human

i.e. respectively:

Given that every human is also an animal, and that there exists an animal that loves all animals, there exists an animal that loves all men.

Given that every human is also an animal and that there exists a human who loves all animals, there exists a human who loves all men.

We translate both versions by introducing the following predicates:

A(x): x is an animal;

H(x): x is a human;

C(x): that must be replaced by A(x) (case i)), or by H(x) (case ii)).

The reasoning is represented as follows in FOL:

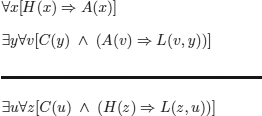
5.2. Semantics

The concepts of interpretation, model, and semantics that we will define are, similar to the concept of meaning in natural language, extremely subtle and deserve some thoughts before providing a formal definition (in FoL).

The notion of a model is essential in logic, computer science, and science generally speaking. It is generally used for many different notions, which is why it is said to be polysemous.

On the general notion of a model

Etymologically:

model → muid → “to prescribe something with authority”.

The word “model” appeared during the 16th Century, meaning measure, musical measure, melody, or way of behaving.

The term is used in different ways in everyday language and in scientific papers. one of the few that can be found in the literature is:

X is a model of Y only if X and Y have the same structure or similar structures.

(This could translate into the existence of a morphism between X and Y)

We can distinguish two meanings that cover many usages:

– representation meant to account for a part of reality that was observed. In general, simplifying hypotheses are allowed, such as idealizations, etc.

A problem that arises involves the limits of the validity of the model, i.e. how can we be sure that all inferences (see Chapter 8) made on the model reflect reality?

A key problem is that of distinguishing between pertinent properties and those that can be discarded. This is of the utmost importance when modeling complex systems, where all the parameters are not well known. Recall the caution of scientists about global warming (models are still not satisfactory).

An example in computer science is that of models of computation, such as, computable functions, Turing machines, lambda calculus, Markov algorithms, DNA computing, and quantum computing;

– the one made in mathematical logic. To provide a model of a logical formula means to give an interpretation of the non-logical symbols (i.e. the constant symbols, functions, and predicates) that permits us to make the formula true.

Note that this notion of a model can also be applied to the axioms of an empirical theory: we can test “real” configurations of the axiomatization of the theory.

This point of view can be useful (as it is in mathematics) to verify that the axioms of the theory are not contradictory: a model from the logical point of view is a possible realization.

A standard method to better grasp a notion for which there is no formal definition (or a definition that is unanimously accepted) is to enumerate the different ways it is used. This is what we do now.

Some differences in the ways the term is used are clear. There is a clear difference between a scale model or blueprint (bridge, etc.) and a mathematical model of the economy, atom, DNA, and kinetic theory.

Two remarks:

– the design of a model is the basis of any scientific activity in natural science. The goal is to select all (and only) those properties, factors, parameters, etc., that are supposed to be pertinent for the studied phenomena;

– the distinction between a theory and a model is not always clear. In general, a model is considered as a step toward a theory.

The notion of a morphism that we mentioned above can be better understood by considering phenomena that are (essentially) described by the same formulas: oscillation of a circuit or a pendulum, flow of a liquid or flow of an electric charge, etc.

Models can have different functions.

For example, in biology, models can have a normative function (see the etymology of the word model at the beginning of this section) to organize data. The capital role here is to classify valid inferences (meaning putting information in a usable form (see Chapter 8 for the definition of this term).

It can also be explanatory (in physics, medicine, etc.) or educational (such as in science popularization TV shows), prospective (social sciences, ecology, etc.), heuristic (computer science, biology, etc.), descriptive (simulation), etc.

On the importance of the notion of a model in science, we quote an opinion of one of the greatest mathematicians of the 20th Century (S. Mac Lane):

5.2.1. The notions of truth and satisfaction

What is truth?

Pilate (Gospel according to John, 18:38)

What I say three times is true

L. Carrol (The Hunting of the Snark)

The notion of semantics (with the meaning of study of a language, i.e. its words and statements from the point of view of their meaning) is very difficult to specify, and our intuition seems to associate it with the notion of translation.

The notions of true and false are closely related to that of meaning.

To give a characterization of the notion of truth is an old problem of philosophy and logic⁶.

As Tarski noticed, the word truth and those derived from it are used in everyday language in different domains: psychology (for example, “Does Ann really love Bernard?”), aesthetism (for example, “Is this book really a masterpiece?”), moral (for example, “Why isn’t this politician telling the truth?”), religion (for example, “Did this miracle really happen?”), etc.

For some, statements are the vehicles of veracity or falsity, for others, meanings are.

Once we agree on this, there remains to decide how to assign them with a truth value (or what their truth value is).

There is, however, a large consensus on the following: what is true or false⁷ are the propositions (see definition 3.1).

A great philosopher (and logician) said it this way: “The eternal statements (i.e. independent from time⁸) are what I consider essentially as vehicles of truth”.

But what does the truth of these statements consist in? They qualify as true (according to Tarski) depending on reality.

“Snow is white” iff snow is white (in other words, truth is disquotation).

The truth predicate is an in-between, between words and statements and the real world. What is true is the statement, but its truth holds because the world is as it states.

By analyzing paradoxes, we can conclude that the truth predicate is incoherent, unless it is somehow restricted (there exists a theorem by Tarski on the undefinability of truth).

Basically, the problem is solved by putting a hierarchy in place, (similar to what was done in set theory): true₀ disquotes all statements without any truth predicate; true₁ disquotes all statements without any truth predicate above true₀… and so on.

Here, we restrict ourselves to the notion of truth in axiomatic systems (mathematical logic) about (well-formed) formulas of a formal language.

Before proceeding with the formalization, a question arises naturally: “What criteria should be satisfied by a suitable definition of truth?”

A. Tarski gave the following three criteria:

1) Meta-language: if L is the object language (working language), then the definition of truth must be given in a meta-language M with L ⊂ M, M must globally be capable of expressing “more things” than L. If L is capable of expressing facts about its own semantics, then we easily obtain paradoxes such as the liar’s paradox.

M contains a unary predicate True whose intended meaning is: True(prop): proposition prop is true;

2) Formal correction: predicate True must be of the form (or in a form provably equivalent to):

If an equivalent form is used, the equivalence must be proved using the axioms of M, but it must not use the predicate True;

3) Material adequation: the objects that satisfy definition (*) in (2) must be exactly those that are intuitively true propositions in L, and this must be proved using the axioms of M.

To avoid problems related to the definition of truth, Tarski introduced the satisfaction relation (see definition 5.6). The key to avoiding problems is that the definition of satisfaction is inductive (it is said to be compositional): we begin with the satisfaction of atomic statements, then the satisfaction of statements of a higher complexity is defined in terms of that of their components (the idea of a hierarchy can be found here too). Truth only deals with closed statements (which do not contain free variables). The analog to truth for open statements is satisfaction. An assignment of objects satisfies a statement if the latter is true for the values given to the free variables⁹. The notion of satisfaction does not permit us to translate, for example, “not (x satisfies x)” (“x” denotes a variable).

To get a better grasp of the idea behind the formal definition, we first give a few informal definitions.

EXAMPLE 5.2.– We consider a “formal system” (see definition 3.9)¹⁰

where:

: English language;

: the “usual” rules of mathematics;

:

let K and L be two sets

A1): every element of L contains exactly two elements of K.

A2): no element of K is contained in more than two elements of L.

A3): no element of L contains all the elements of K.

A4): the intersection of any two (distinct) elements of L contains exactly one element of K.

A possible model, interpretation, and meaning of these axioms (that also shows that these axioms are not contradictory) is:

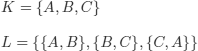
(this model can be viewed as a triangle with the (non-collinear) vertices A, B, C).

EXAMLPLE 5.3.– (Z. Manna and R. Waldinger). When learning algorithm, it turns out that program schemas frequently occur in different problems.

Consider the following schema, for which we will produce different interpretations.

 

program X;

begin

read (x) ;% x is a variable

y₁ ← x ;

y₂ ← a ; % a is a constant

while ¬P(y₁)

do

y₂ ← g(y₁, y₂) ;

y₁ ← f(y₁) ;

enddo

z ←y₂ % z contains the result

end

– Interpretation 1

D (considered universe):

a: 1

f(y₁): y₁ − 1

g(y₁,y₂): y₁ × y₂

P(y₁): y₁ =0

The program represents factorial (x)

– Interpretation 2

   D (considered universe): lists

   a: nil

   f(y₁): cdr(y₁) %, i.e. list y₁ without its first element

   g(y₁,y₂): cons(car(y₁),y₂) %, i.e. the list obtained by putting the first element of y₁ instead of that of y₂

   P(y₁): null(y₁) % null(y): y is an empty list

 

The program represents reverse (x)

– Interpretation 3

   D (considered universe):

   a: 0

   f (y₁): y₁ - 1

   g(y₁,y₂): y₁ + y₂

   P(y₁): y₁ = 0

 

The program represents the sum of the first x natural numbers.

EXAMPLE 5.4.– Consider the following wffs:

a) ∀_x(¬P(x, x) ∧ (∀y∀z((P(x, y) ∧ P(y, z)) ⇒ P(x, z))) ∧ ∃wP(x,w))

    This could express (for example): no natural number is less than itself, the relation “less than” is transitive and there always exists a natural number that is greater than a given natural number.

b) ∀y∃xP(x, y)

    This could express (for example): every integer is greater than some other integer.

c) ∀y∃xP(x, y)

    We could say this is false if we consider natural numbers and P represents the relation “less than”.

d) ∀x¬D(a, x)

    This could express (for example): 0 does not divide any integer.

e) ∀xP(f(x))

    This could express (for example): the square of any integer is positive.

f) ∀x∀y(P(x, y) ⇒ P(x, y))

    This could express (for example): for any relation we could imagine that is represented by P, this wff is true.

g) ∃x∃y¬(P(x, y) ⇒ P(x, y))

    This could express: for any relation we could imagine that is represented by P, this wff is false.

    Consider the following wff:

h) ∀x∃yP(x, y)

    is it true or false? The (correct) answer that seems the most natural is, it depends. Indeed, if the formula is interpreted on and P(x, y) represents the relation x ≤ y, then it is true. If P(x, y) represents x > y, then it is false.

i) ∀x∃y(P(x, y) ∧ ∀w(P(y,w) ⇒ y = w))

This could represent: if the values of variables x, y and w are instants and P(x, y) denotes the relation x ≤ y between these instants, the formula expresses that there will be an end of time.

DEFINITION 5.4.– Given a first-order language (see definition 5.1), a first-order structure or structure is a triplet:

where:

D is a non-empty set called the domain or universe of discourse

set of functions:

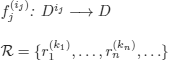
set of relations:

where the 's (in particular, the constants) and the 's, respectively, correspond to the functional symbols and the predicates in .

Two particular cases:

EXAMPLE 5.5.–

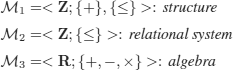
DIGRESSION 5.3.– When searching for interpretations of wffs or sets of wffs, it is often the case that different interpretations are “globally” the same.

More precisely, to each element of one domain corresponds an element of the other domain with the same properties and conversely.

This feature is formalized in the following definition.

DEFINITION 5.5.– (structure isomorphism). Given two structures and :

a bijection

is a structure isomorphism iff

(the exponents and identify the structure the objects belong to)

– for every constant c in the signature of :

-for every n-tuple and every n-ary functional symbol f⁽ⁿ⁾ in the signature of :

–for every n-tuple and every n-ary predicate symbol P⁽ⁿ⁾ in the signature of :

and are said to be isomorphic.

REMARK 5.5.– The idea behind the following definition is the same as the one that we used informally and intuitively in the examples, i.e. given a first-order language (or wff), we fix a universe D, to each constant in the wff we associate an element of D, to each functional symbol of arity n, a total function (meaning that it is defined everywhere on D) of arity n on D, and to each predicate symbol of arity k, a relation of arity k on D. Variables “go through” D, and ∀ and ∃ are interpreted as usual, i.e. “for all” and “there exists (at least one),” respectively. The semantics (meaning) of the wff is given by that of the functions and relations on the chosen universe, which are assumed to be known.

 

A cwff is T or F in an interpretation. The evaluation of the cwff is carried out in the structure and the variables get their values in the universe of discourse. It is, therefore, not necessary to add to the language expressions of the form “for every x in D”. The language is independent of the formalization of set theory.

DEFINITION 5.6.– (interpretation, satisfaction). Let denote a first-order language and a structure.

An fp-assignment (f stands for “function” and p stands for “predicate”) is a function a_fp satisfying the following:

i) for every predicate symbol is a relation of ;

ii) for every function symbol :

is a (total) function

for constants:

a υ-assignment is a function:

where denotes the set of variables of .

For terms (see definition 4.1) we define the t-assignment a_t as follows:

iii) if then a_t(t) = a_v(t);

iv) if then a_t(t) = a_fp(t);

v) otherwise, .

– An interpretation of the language (or of a wff of ) is an fp, v, and t-assignment.

– A satisfaction relation:

(which reads as “Formula is satisfied in structure with interpretation ”)

is defined as follows:

1)

2) iff not %, i.e. logic with two truth values

3) and

4) or

5) or

6) and

7) see section 9.1

8) iff there exist a such that

9) iff for all

coincides with except for a_v(x)

REMARK 5.6.– Warning: not () is not equivalent to .

See section 3.1.1 and remark 3.5. The negation of “for all” is not “for all not”.

REMARK 5.7.– (on the domain of discourse). In the definition of the semantics for FOL, the only constraint on the domain of discourse is that it is non-empty. We can therefore choose the domain of discourse to be a set of closed terms. This remark will be useful in the proof of theorem 5.4.

EXAMPLE 5.6.– The wff

denotes in what is called Presburger arithmetic, i.e. the theory of the structure:

“There are infinitely many even numbers”.

This theory is decidable, but the decision procedure has a superexponential complexity (2²ⁿ).

DEFINITION 5.7.– A wff φ is valid iff it is satisfied in every interpretation on every structure. This is denoted by .

A structure is a model of a set of wffs S iff there exists such that for all .

REMARK 5.8.– (models: another theory). A model of an axiomatic theory is a set of objects chosen from another theory: the one in which the objects assigned to those of the former are supposed to have a meaning “by themselves” (for example, sets, functions, and relations) and satisfying the axioms.

REMARK 5.9.– (open and closed formulas).

– A cwff denotes a truth value. For example, ∀x∃yP(x, y) denotes true in , if P represents <.

– An owff denotes a set, i.e. the set of values that make it true. For example, Prime(x) denotes all prime numbers.

– Owffs are used to define classes (sets) (see digression 2.2), for example, the set {x | Prime(x)}.

– Free variables, and therefore owffs, occur very frequently in informal mathematics, in expressions such as:

i) Let x denote a natural number

or :

ii) Let x denote a natural number such that…

In (i) they are given a universal interpretation (i.e. for all x).

In (ii) they are given a conditional interpretation (i.e. for some particular x’s).

When these expressions (or rather their formalizations) are involved in reasonings, they will be treated, as is customary, as universally quantified variables. Indeed, when no particular conditions are imposed on x, this is equivalent to saying for any x, or for all x.

EXAMPLE 5.7.– (set of prime numbers). The set of prime numbers in can be defined as follows:

.

When a condition is imposed on x, this is equivalent to saying for all x satisfying this condition (condition that will be translated in the formula)¹¹.

– For the owffs that occur in reasonings, we shall use their closure, which is defined by:

(where Free_vars)

EXERCISE 5.1.– (A model is finite (respectively, infinite) if the cardinality of its universe of discourse is finite (respectively, infinite).

a) Give a model of:

b) Give a model and a counter model of:

c) Give a model of:

d) Give a model of:

e) Give a model of:

f) Give a counter model of:

g) Give a model and a counter model of:

h) Is the wff:

valid?

i) Give a model of the following formula that is independent of the selected domain of discourse.

   In other words, give an interpretation of the predicate P such that for any domain, it corresponds to a model of the given formula:

j) Given the wff:

j₁) give a model of this formula with domain D = (i.e. an infinite model);

j₂) give a model of this formula with domain D = {1, 2} (i.e. a finite domain);

j₃) give a counter model of this formula with domain D = .

k) Can you construct:

k₁) a finite model for the following formula?

k₂) an uncountably infinite model?

k₃) a denumerably infinite model?

1) Give a model and a counter model of:

m) Can you construct:

m₁) an infinite model for the formula:

m₂) a finite model?

n) Can you construct a finite model for the formula:

i.e. a function f : D → D that is one-to-one but not onto.

o) Given the formulas (1), (2), and (3) below, show that (3) is not a logical consequence of (1) and (2) (in other words, the commutativity of + cannot be deduced from (1) and (2))

0 denotes a constant, x and y variables and s a functional symbol.

p) Can you construct a model for the set of formulas below?

a denotes a constant, x and y variables, and f, s, and p functional symbols.

5.2.2. A variant: multi-sorted structures

In section 5.2.1, it was mentionned that it was not necessary to specify what domain a variable can get its values from in a formula.

However, it is common in practice to want to identify these domains (sets that are named sorts), in particular, when different variables can get their values from domains of different types (for example, scalars and vectors in vector spaces).

5.2.2.1. Expressive power, sort reduction

We may wonder whether using sorts increases the expressive power of FOL, i.e. if more things can be expressed with sorts than without or if this is simply syntactic sugar. The answer is that the expressive power of FoL with sorts is the same as that of FoL, and this result is proved using the so-called sort reduction technique.

– The signature is extended with predicates P_D and P_E.

– We consider the structure

where R_D = D, R_E = E (R_D and R_E, are unary relations, i.e. subsets of D and E, respectively) and:

a_fp(P_D) = R_D and a_fp(P_E) = R_E (see definition 5.6).

– Hence, if sorts were used to write formulas, it suffices to replace (as usual, F [x] means that variable x occurs in wff F):

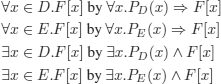
REMARK 5.10.– (theory, closed theory, and complete theory). In definition 3.9, we defined the notion of a formal theory. Here, we introduce the notion of a theory, along with essential definitions and properties of theories, that deal with semantics.

– Once the notion of consequence has been introduced (see definitions 2.4 and 2.6, it can be syntactic or semantic), a theory is closed iff it is closed by the consequence relation (according to Gödel’s completeness theorem, see remark 5.21, we can use or ).

–A theory T is complete (in ) iff the set of its consequences is maximal consistent (i.e. if it is consistent and none of its supersets is consistent).

– A set of axioms of a theory T is a set of cwff with the same set of consequences as T. T is a set of axioms of T and ∅ is a set of axioms of T iff T is the set of valid cwffs of (from a semantical point of view). T is finitely axiomatizable iff it is axiomatizable by a finite set of axioms.

– (See remark 3.15) The standard way of specifying a theory is to provide a set of axioms that define it.

Here is another way of proceeding: given a structure and an interpretation of , the theory is the set of all cwffs F of such that Theory is complete.

– A theory T is complete iff for all cwffs F, either T F or T ¬F. % This is to be compared with the notion of completeness for a formal system (definition 3.12).

Given a theory T, statements 1 to 4 below are equivalent:

1) the set of consequences of T is maximal consistent;

2) T is complete (i.e. for all cwffs F, either T F or T ¬F);

3) T has exactly one model;

4) there exists a model such that for all cwffs F, T F iff F.

5.2.3. Theories and their models

Two isomorphic structures (see definition 5.5) do not differ on anything essential.

The following theorem confirms this intuition and shows that FOL does not permit us to distinguish between two isomorphic structures.

THEOREM 5.1.– (structure discrimination). Let ₁ and ₂ denote two isomorphic structures. Then, for all wffs F of FOL,

PROOF.– (intuition). By structural induction (i.e. for all objects introduced by the inductive definition of wffs, see definition 5.1).

It is legitimate to wonder whether the converse is also a theorem.

The negative answer to this question is given by the following theorem:

THEOREM 5.2.– (non-standard model). There exists a set of formulas S of FOL that admits the structures and as models (see the definition below), where ₁ and ₂ are not isomorphic (example given by Crossley et al.).

 

PROOF.– Consider the following set of formulas (we indicate as a comment, i.e. a line preceded by %, the desired interpretation of predicate P):

It is simple to check that:

(where denotes the usual order relation in ) is a model of S.

Now consider the following sets:

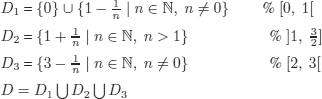
and the structure (where denotes the usual order relation in ).

It is simple to verify that this is also a model of S.

But ₁ and ₂ are not isomorphic structures, as can be verified by taking an element of D, for example, (or or , etc.), which has an infinity of predecessors, which is not the case for any element of (see digression 5.3 and definition 5.5).

₂ is called a non-standard model because it is not isomorphic to the intended model ₁, which is called the standard model.¹² Note that Peano’s axioms are categorical in second-order logic (SOL).

5.2.3.1. How can we reason in FOL?

Similar to what was done in PL, we can provide a syntactical approach (with a formal system) or a semantical approach (based on interpretations). We shall give priority to the latter.

Actually, the methods will be obtained thanks to semantic notions, but similar to what was done, for example, for resolution in PL, the goal is to obtain a deductive system.

For the syntactical approach, see remark 5.21.

5.3. Semantic tableaux in FOL

It is obtained by reduction to the method of semantic tableaux in PL.

There are two fundamental differences compared to the method studied for PL (these differences are inherent to FOL):

– the quantifiers and may occur;

– the method may not halt (FOL is undecidable).

The way we proceed is basically intuitive and is based on the same ideas as the corresponding formal system.

The Lowenheim-Skolem theorem (theorem 5.4) ensures that it is possible to restrict the search for models of FOL formulas to denumerable domains.

From now on, we therefore restrict ourselves to denumerable universes (interpretations and models), which are the only ones that can be handled in computer science.

This enables us to solve the problem of handling quantifiers. On a denumerable universe

and correspond to:

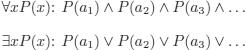
(these are not wffs of FOL, but an informal way of stating things).

There are two important questions that need to be asked:

– when variables are replaced by elements of the domain D, what we obtain is generally not a wff of FOL (see definition 5.1). However, intuition, together with the habits of mathematical practice, suggest that “this does not matter”. Indeed, in mathematical practice, it is not necessary to declare signatures, and symbols are introduced when they are needed. Furthermore, in general, the domain of discourse (semantical point of view) shall be described using a set of symbols that is disjoint from the one used to write formulas (syntactic point of view). We can therefore assume that, each time we are searching for models of FOL formulas (or proving that they do not have any), we have at our disposal a denumerably infinite set of parameters, denoted by Par (where Par, see definition 5.1), that will replace the variables occurring in formulas and will also denote the values of closed terms;

– the second key point is that, in the proof of the Löwenheim-Skolem theorem (theorem 5.4), we assume that the considered formula F is in Skolem normal form (written sk(F)), i.e. in a form that is not necessary to treat the formula with the method of semantic tableaux.

A capital operation to obtain sk(F) is the elimination of existential quantifiers by Skolemization. When replacing ∀x∃yP(x, y) by ∀xP(x, f(x)), Skolemization introduces a function f (which is not defined, but whose existence is guaranteed by the AC). This function can be replaced by its graph with domain and codomain Par, meaning that ∀x∃yP(x, y) will be replaced by P(a₁, a₂), P(a₁, a₂),…

Using an argument similar to the one that occurs in the proof of the Lowenheim– Skolem theorem, we could think: if the formula ∀x∃yP(x, y) has a model with uncountably infinite domain D, this means (see definition 5.6) that for all x ∈ D, there exists x ∈ D such that (where is the relation assigned to P in the model). But if this is true for all x ∈ D, it must also hold for a denumerable subset of D, and, in particular, up to a renaming, on the domain Par; see also section 5.4.

A similar reasoning applies to formulas that are exclusively quantified with ∀’s.

We shall use the following equivalent formulas (not doing so can lead to errors; see exercise 5.3):

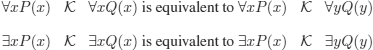
where

as well as:

where denotes a wff.

REMARK 5.11.– The last four rules are frequently used. For example, to express that function f is not injective:

is equivalent to:

which is equivalent to:      

which is equivalent to:

The rules to use for the method of semantic tableaux in FOL are those of section 3.2, together with the equivalent formulas above and the rules of Figure 5.1.

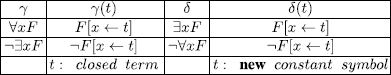
REMARK 5.12.– It should be clear that, although they are syntactically different from propositions (base formulas), atomic formulas such as P(a₁) where a₁ is a constant, correspond to the definition of propositions and it is correct to consider them as such. Atomic formulas such as P(x) are often called propositional functions.

To illustrate the ideas, recall H(x) (x is a man). It cannot be evaluated as long as the value of x is not known. This is not the case for H(a) (Socrates is a man) or H(b) (The mother of Socrates is a man).

As for PL, a branch will be closed once an elementary contradiction has been detected (for example, of the form P(a), ¬P(a)), and those are the only ones that can be detected syntactically (i.e. mechanically).

REMARK 5.13.– The procedure semantic tableaux (FOL) is non-deterministic, in other words, choices are free. But when we fail to close a tree, we may wonder if this is due to the fact that it is indeed impossible to close the tree or if we simply chose a bad strategy that indefinitely delayed some choices that would have permitted us to close the tree. Such a strategy is unfair.

Of course, this does not mean that using a fair strategy (i.e. a strategy that never delays a choice indefinitely) can transform an undecidable problem into a decidable one, but it permits us to eliminate some artificial non-terminating cases.

The following example is convincing.

EXAMPLE 5.8.– Assume that we want to show the soundness of the following reasoning (a denotes a constant):

If we apply a fair strategy, we easily prove that this is a correct reasoning:

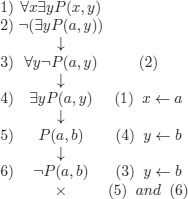
However, if some choices are delayed indefinitely:

EXAMPLE 5.9.– Consider the famous syllogism “Every man is mortal. Socrates is a man. Therefore, Socrates is mortal”. Its translation in FOL is:

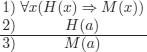
where:

H(x): x is a man.

M(x): x is mortal.

a: Socrates.

To prove that the reasoning is correct, we consider the set

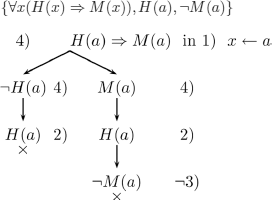
EXAMPLE 5.10.– Consider the reasoning:

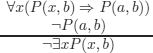
We try to construct models for the set of wffs 1, 2, 3 below (2 is the negation of the conclusion).

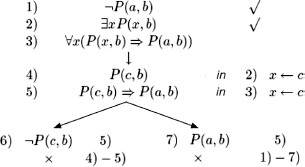
Note that, in this example, we used some general principles in the method (indicated in the algorithm) that correspond to normal practices in mathematics:

– we replaced ∃x by c, a fresh constant (that did not occur in the considered wffs);

– once we have introduced a constant in place of ∃x, we are no longer allowed to use (2) (which is why we mark (2) as used ());

– in (3), variable x can potentially be replaced infinitely many times, which is why it cannot be marked as used. We see that can cause trees to be infinite;

– similar to the case of PL, in which each wff that we used was (implicitly) marked, we mark (1) with .

EXAMPLE 5.11.– A problem arises: what happens if the reasoning that we are verifying is not correct, in other words, if the associated set of wffs is not contradictory? The answer is the same as in PL: there will be open branches. But the difference is that there may be infinite branches in FOL. We examine a case in which the method halts and others in which it does not.

We thus consider the set of wffs 1,2 below

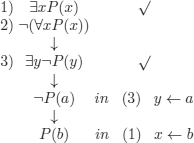
We halt without being able to close the tree. We have a model of the set of wffs, i.e. a counter example of the initial reasoning. The meaning of the open branch is simple: it is a unary relation (i.e. a property) corresponding to P that is true for b (i.e. b belongs to the relation) and false for a (i.e. a does not belong to the relation). This interpretation makes the premises true and the conclusion false.

More formally, an interpretation can be extracted from the open branch of the tableaux (see definition 5.6), which is a counter example of the proposed reasoning:

with:

in

In other cases, it is not possible (for the method, a human would easily realize that it will not halt).

If we want to test the validity of the wff:

we test the unsatisfiability of:

“we can see” that the method is trying to construct an infinite model (think of D: N and P(x, y): x < y).

EXAMPLE 5.12.- We want to test whether the following reasoning is correct using the method of semantic tableaux.

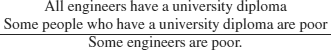
This is formalized in FOL using the following predicates:

I(x) : x is an engineer;

D(x) : x has a university diploma;

P(x) : x is poor.

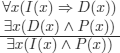
We thus try to construct models of the premises and of the negation of the conclusion.

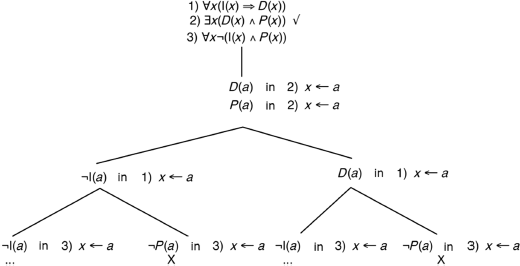
The leftmost branch cannot be closed (the method does not detect this property, see also theorem 5.11) and provides a counter example of the initial reasoning: someone who has a university diploma (D(a)), who is poor (P(a)), and who is not an engineer (¬I(a)). We could imagine a universe containing only a poor lawyer, or a universe in which none of those who are poor and have a university diploma are engineers.

Of course, there can be poor engineers, but the proposed reasoning does not prove this.

EXAMPLE 5.13.– A seldom explored characteristic of semantic tableaux is the possibility to detect in some cases the n-validity of a formula (which means that a formula is valid in every universe D such that card(D) < n, n ∈ ) but can be falsified in any universe of a greater cardinality. We use the method of semantic tableaux to show that the wff

where:

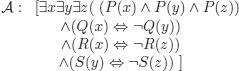
is three-valid.

states (see Leibniz's law, section 9.1.4) that there exist three distinct objects x, y, z.

The last three conjuncts express the fact that each of the tree objects is different from the other two, as a given object cannot have and not have a property.

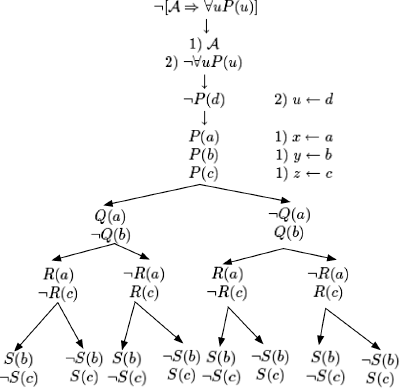
We analyze what happens in universes of cardinality 1, 2, 3 (branches are identified with the standard notation on trees):

card(D) = 1

a = b = c = d contradiction in branch 1.

card(D) = 2

a = b = c contradiction in branches 1.1 and 1.2.

a = b = d contradiction in branch 1.

a = c = d contradiction in branch 1.

b = c = d contradiction in branch 1.

a = b and c = d contradiction in branch 1.

a = c and b = d contradiction in branch 1.

a = d and b = c contradiction in branch 1.

card(D) = 3

a = b contradiction in branches 1.1 and 1.2.

a = c contradiction in branches 1.1.1; 1.1.2; 1.2.1; and 1.2.2.

a = d contradiction in branch 1.

b = c contradiction in branches 1.1.1.1; 1.1.1.2; 1.1.2.1; 1.1.2.2; 1.2.1.1; 1.2.1.2; 1.2.2.1; and 1.2.2.2.

b = d contradiction in branch 1.

c = d contradiction in branch 1.

For universes D with card(D) ≥ 4, no branch can be closed (the open branches provide counter models of the initial formula).

REMARK 5.14.– In this example, we implicitly violated the requirements of rule δ (i.e. that every constant introduced by an existential quantifier must be a fresh constant that is not introduced by any other existential quantifier).

This violation allows us to enumerate the models of all cardinalities for which a non-valid formula can be satisfied.

It is not difficult to show that we have extended the method without losing its soundness and completeness properties.

We may wonder whether this example can be generalized to any arbitrary n. This is the topic of the following exercise.

EXERCISE 5.2.– Can we give a wff in FOL that specifies the n-validity for (i.e. for an arbitrary and fixed value of n)? (See also example 9.31.)

EXERCISE 5.3.– Can you prove that following reasonings (respectively, wffs) (a) to (l) given below are correct using the method of semantic tableaux?

a)

b)

c)

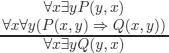
d) Prove that: every irreflexive¹³ and transitive relation is asymmetrical.

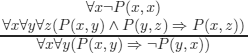
e)

f)

g)

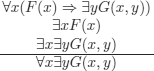
h)

i)

j) Add a premise to the reasoning of example 5.12 so as to make it correct.

Give the corresponding closed tableaux.

k) Use the method of semantic tableaux to determine if the following formula:

   k1) is not valid, and if this is the case, extract a counter example from the tableaux;

   k2) is valid, and in this case give a model obtained using the method of semantic tableaux.

1) a, b, c, d, e denote constants.

1) P(a, b)

2) P(b, c)

3) P(c, d)

4) P(d, e)

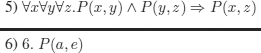
EXERCISE 5.4.– Use the method of semantic tableaux to tell whether the following reasoning is correct or not.

If it is incorrect, extract a counter example of minimal cardinality from the tableaux.

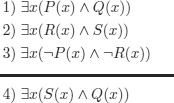
5.4. Unification in the method of semantic tableaux

In the method of semantic tableaux for FOL, there are two main problems, the first with rule γ, which corresponds to the instantiation of universally quantified variables, and the other with rule δ, which corresponds to the introduction of fresh and unique constants as instantiations of existentially quantified variables.

– The problem with rule γ, which may generate infinite branches, is to find adequate instances so as to close the branches (that can be closed) at the least possible depth.

A solution that is frequently adopted in implementations is to replace a universally quantified variable, say x, by a (free) variable X.

This renaming shall be written as x → X.

Of course, the “disappearance” of the universal quantifiers must not hide the fact that the free variables that were introduced can be replaced by any number of terms. To keep this property, we introduce renamings of the free variables that we shall note: x → X₁, X₁ → X₂ X₂ → X₃,…

– The problem with rule δ is that, when there will be, say, n free variables X₁, X₂, …, X_n that have been introduced in the branch corresponding to formula F, where appears in the scope of X₁,…, X_n, as usual, will be erased, and y will be replaced by f(X₁, X₂,…, X_n), where f is a new functional symbol called a Skolem function. This guarantees the introduction of a new name (constant) each time there is an instantiation of an existentially quantified variable, which is in the scope of universally quantified variables (syntactically different terms correspond to different names), i.e. the most general case.

(This is what we have done systematically, for example, in example 5.11)

– The unification algorithm is used to find the instantiation that allows us to close branches or to detect whether they (still) cannot be closed, therefore, suggesting renamings of the free variables (and implicitly of the existentially quantified variables that are in the scope of the free variables).

EXAMPLE 5.14.- (unification in semantic tableaux, 1). Prove the validity of the formula:

Note that in formulas 11 and 12, we have the same X.

EXAMPLE 5.15.– (unification in semantic tableaux, 2). Prove the validity (or non-validity) of the formula:

therefore, the formula is not valid.

EXERCISE 5.5.– Show that the following reasoning is correct using the method of semantic tableaux with free variables (i.e. using unification).

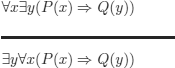
5.5. Toward a semi-decision procedure for FOL

It is impossible to design a decision procedure for FOL. Indeed, FOL formulas can be used to describe any Turing machine, and deciding the validity of an arbitrary wff is equivalent to solving the halting problem (which is undecidable).

But there is nothing stopping us from searching for a semi-decision procedure for this logic (only hope for the automation of such a procedure)¹⁴, i.e. a procedure that, if it stops, gives a correct answer, but for which we cannot say anything if it has not stopped at a given moment.

To test if a formula is satisfiable or valid, we (potentially) have to test infinitely many universes, which is impossible. We will see that it will suffice to restrict ourselves to a priviledged universe that will have “good properties”. The first step in this direction is to transform the formulas into a normal form.

5.5.1. Prenex normal form

When we consider a set of objects that can have many different forms, it is desirable to have a transformation into a normal form. It permits us, for example, to study the properties of these objects in a uniform manner and to state these properties more easily.

DEFINITION 5.8.– A wff of FOL F is in prenex normal form, (denoted by pr(F)) iff it is of the form:

(n = 0 means that the formula contains no quantifier) where Q_i: ∀ or ∃

Q₁x₁… Q_nx_n is called the prefix.

: does not contain any quantifier and is called the matrix.

We implicitely assume that (see definition 5.1) if Q_i ≠ Q_j, then x_i ≠ x_j (meaning that a same variable is not quantified by different quantifiers).

THEOREM 5.3.– (existence of the prenex normal form). If F is a wff of FOL, then there exists an equivalent pr(F).

PROOF.– (outline). Apply the equivalent transformations below and reason by induction on the number of connectives.

The rules assume that (rename if necessary)

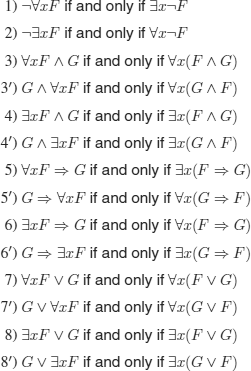
1, 2, 3, 4 are sufficient (the other rules can be applied using the equivalent formulas of exercise 3.2).

 

EXAMPLE 5.16.– We can use (this is what we will do in exercise 5.7) the method of semantic tableaux to prove the validity or non-validity via a counter example of expressions denoting wffs that we will call “generic formulas” i.e. sets of formulas with a given structure, that can be characterized by naming their subformulas.

We prove below the validity of rule 5, which is used in the proof of theorem 5.3.

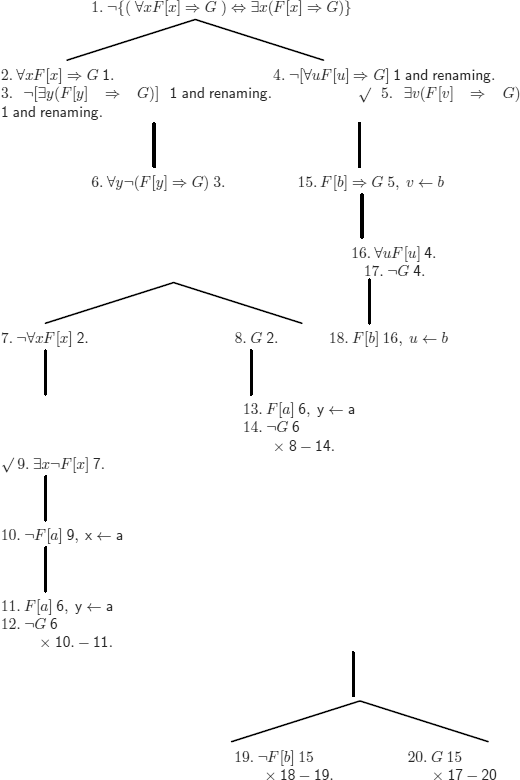
We will also use the information provided by the method of semantic tableaux to construct a counter example of an incorrect transformation rule that we might be tempted to use: as subformula G does not contain the quantified variable x, we can include G in the scope of ∀x.

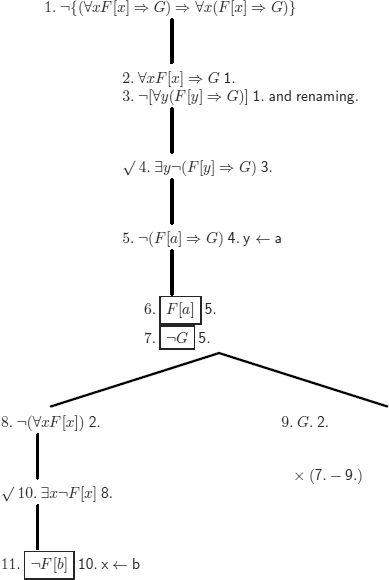
We can extract a model from the negation of the formula (i.e. a counter example of the considered formula) in the open branch (there are no longer any universally quantified formulas: 2 was replaced by 8 and 9), by taking, for example:

(This replacement respects the initial hypotheses.)

and the structure

with:

and:

The counter example constructed by the tree corresponds to:

This is indeed a counter example, the verification is immediate:

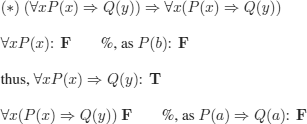
(∗) is therefore evaluated to F in the proposed interpretation.

 

Is the prenex normal form unique? The following example shows that this is not the case.

EXAMPLE 5.17.– (non-uniqueness of the prenex normal form). The order of application of the rules can lead to different prenex normal forms for the same formula. Consider the formula:

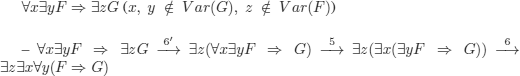
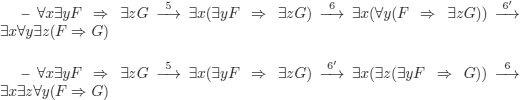
The prefix of the prenex normal form contains existential quantifiers. To establish fundamental theorems for the automation of FOL, we must introduce an operation permitting to eliminate them.

5.5.1.1. Skolemization

Skolemization (from the Norwegian logician T. Skolem) enables us to eliminate existential quantifiers while retaining the satisfiability of a formula.

The idea is that:

admits a model, and f is a function symbol that does not appear in the considered formula

iff:

admits a model.

but () and () are not equivalent, i.e. are not evaluated to the same truth value for the same interpretations.

More generally:

the formula:

yields by Skolemization:

and if m = 0:

We will show, using the method of semantic tableaux, that:

meaning that there exist models of ∀x∃yP(x, y) that are counter models of ∀xP(x, f(x)).

We will therefore try to construct models of:

and if we succeed, we will have proved ().

Using this tableaux, it is simple to construct the desired counter example (by letting f(a) ≠ b):

with:

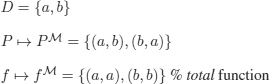
Note that the tableaux guarantees that we can always (if transform a model of ∀x∃yP(x, y) into a model of ∀xP(x, f(x)) (by letting f(a) = b).

This non-equivalence (sometimes called weak equivalence) is not really a problem when we try to prove that a wff does not have any model (i.e. that its negation is valid).

If we wanted equivalence to be preserved, we would have to replace:

by:

∃f∀xP(x, f(x)), but this formula is not a wff of FOL (see the syntax of FOL in definition 5.1 and exercise 9.5).

REMARK 5.15.– Another way to prove that Skolemization does not preserve equivalence (but only satisfiability) is to consider the following counter example.

The formula:

is valid (as can easily be checked using the method of semantic tableaux or by noticing that this formula is equivalent to ∀xP(x) ⇒ P(a)).

If we transform (), we first obtain:

and using Skolemization:

which is a satisfiable but not valid formula (as P(a) can be evaluated to F and P(b) to T).

5.5.2. Skolem normal form

Starting with a FOL formula F, after transformation into prenex normal form and Skolemization, we obtain the Skolem normal form of F (denoted by sk(F)):

sk(F): ∀x₁ … ∀x_nF′, where F' does not contain any quantifier and Var(F') = {x₁… x_n}

Therefore, by theorem 5.3 and the Skolemization property:

() F wff of FOL is satisfiable iff sk(F) is satisfiable

DEFINITION 5.9.– (universe, base, Herbrand interpretation). Given a finite set S of formulas in Skolem normal form constructed on the set of predicate symbols π and function symbols , the Herbrand universe on (or Herbrand universe of S) is defined as follows:

if F does not contain any constant, then H₀ = {a};

– .

(With the notation of definition 4.1, we should note Σ(F) instead of H(S).)

The terms in H(S) are obviously closed (see definition 4.1) and are called Herbrand terms.

The Herbrand base of S is the set of positive literals (i.e. of atomic formulas):

– or

where means all variables in L are replaced by Herbrand terms. is a Herbrand instance or simply constant instance or closed instance of . We shall also talk of (see definition 5.10) closed clauses.

AF_c: closed atomic formulas in S.

Notation: here, as is customary, denotes an n-tuple of variables and denotes an n-tuple of Herbrand terms.

– A Herbrand interpretation of a set of universally quantified formulas S constructed on (π, ) is an interpretation _H(S) such that:

D = H(S)

if

if

with:

(and of course t_i ∈ H(S); 1 ≤ i ≤ n)

if

with

– A Herbrand interpretation can be represented by .

The obvious intuitive meaning is that the literals are evaluated to T on the n-tuples or that .

The set of Herbrand interpretations of S is thus the set of subsets of B(S).

REMARK 5.16.– The Herbrand universe corresponds to what is called the term algebra in universal algebras., i.e. (see definition 5.4):

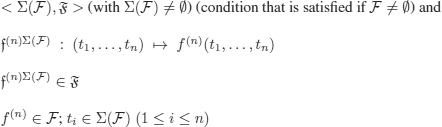
EXAMPLE 5.18.– S = {C₁, C₂, C₃}

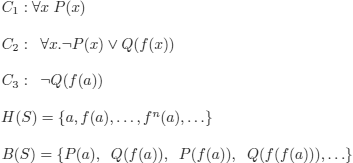
a Herbrand interpretation:

meaning that P(a) is evaluated to T and that P is evaluated to F on all other elements of H(S). Q(f(a)) is evaluated to T and Q is evaluated to F on all other elements of H(S).

Another Herbrand interpretation:

meaning that P is evaluated to T on all elements of H(S), and Q to F on all elements of H(S).

EXERCISE 5.6.– Let denote the following set of wffs:

Can you give three Herbrand models of ? Which ones?

REMARK 5.17.– By construction, the Herbrand universe (and the Herbrand base) of a set of formulas S is either finite (if no function symbol occurs in S) or denumerably infinite.

As a consequence, the number of Herbrand interpretations for a set of formulas S is either finite or uncountably infinite (see exercise 3.1).

For example, we can give an uncountably infinite model of the formula , for example, , and we can also give a denumerably infinite one, for example, . This example is a particular instance of the following theorem.

THEOREM 5.4.– (Löwenheim–Skolem). If a FOL wff F has a model, then it also has a denumerable model.

PROOF.–

– It suffices to consider sk(F), see () in section 5.5.2.

– We assume that D is the domain of discourse of the model of sk(F).

– If a universally quantified wff (such as sk(F)) is satisfied on a domain D, then it is also satisfied on a domain D′ ⊆ D (see definition 5.6 and remark 3.39).

– We consider H(sk(F)) from which we will construct a denumerable set D′.

– We begin by the (necessarily finite) set of constants in F or by the additional constant, which will denote, in the model, elements of D. These will also be elements of D'.

– The terms f^(n)H(sk(F))(t₁, …, t_n) denote elements of D in the model (see definition 5.6) that are added to D' (D' is closed by this operation, by definition of a Herbrand universe).

– By construction D' is either finite or denumerably infinite (see remark 5.17). This proves the theorem.

EXAMPLE 5.19.– Consider the wff:

with the intended interpretation: for all reals there exists a greater real;

we obtain by Skolemization:

A model can be constructed on the structure:

where

if, for example, we fix , we obtain

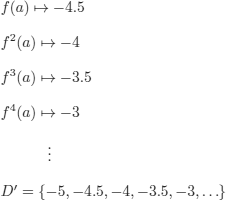
A Herbrand model:

We have the following immediate corollary:

COROLLARY 5.1.– (Löwenheim-Skolem for finite sets of formulas). If S is a finite set of FOL wffs that admits a model, then S admits a denumerable model.

PROOF.– Let S = {f₁, f₂,…, f_n}.

By definition (see definition 3.8) S has a model iff there exists a model that satisfies all the formulas in S, i.e. iff:

The corollary is proved by applying theorem 5.4 to F.

REMARK 5.18.– The Löwenheim-Skolem theorem also applies to denumerably infinite wffs of FOL: if S is a denumerably infinite set of wffs of FOL that has a model, then S has a denumerable model.

REMARK 5.19.– (an important consequence of the Löwenheim-Skolem theorem). An immediate consequence of the Löwenheim-Skolem theorem is that the intended interpretation of a wff of FOL is not unique: there can also be unintended interpretations.

As a consequence, FOL formulas cannot characterize uncountably infinite sets¹⁵, because we know that along with such a set, they will also admit a denumerable model (i.e. they will also characterize a denumerable set).

The Löwenheim-Skolem theorem permits us to imagine a mechanical validity test (as it will be performed on denumerable domains).

There remain two questions that, if answered positively, make the existence of such a test impossible:

– would we have to test all interpretations on a given denumerable domain?

– would we have to test all denumerable domains?

The answer to both questions is (fortunately) negative.

REMARK 5.20.– (on interpretation domains). Before we formalize these answers, note that the only requirement on the domain of an interpretation is that it should not be empty. It can, in particular, consist of terms without variables (closed terms) constructed on the same signature as (the Skolem normal form) of the initial formula.

The negative answer to the first question is a result of the following theorem.

THEOREM 5.5.– We can test the validity of a wff of FOL on a denumerable domain without taking interpretations into account.

PROOF.–

– Let F denote the wff whose validity we want to test.

– ¬F is satisfiable iff is sat (see section 5.5.2).

– F is valid iff ¬F is unsatisfiable.

– ¬F is unsatisfiable iff sk(¬F) is unsatisfiable.

– To test the validity of F, we therefore test whether sk(¬F) is unsatisfiable.

– Let D denote the domain on which we want to test the unsatisfiability of sk(¬F); D = {a₁, a₂,…, a_n, …}.

– We assume that (Var is the set of variables and all variables are universally quantified by definition of the Skolem normal form).

– We want to enumerate the k-tuples of elements of D, that will be denoted by .

% A bijection can be defined by:

– Testing the universally quantified formula sk(¬F) reduces to testing sk(¬F) on all the elements of D^k.

– We therefore consider k-tuples of variables of sk(¬F).

– If is unsatisfiable then such that is unsatisfiable (propositional test; contrapositive of the compactness theorem for PL, theorem 3.3).

– This test is independent of the interpretation of the function symbols (and, in particular, of the constants) and of the predicates.

The negative answer to the second question is given by the following theorem.

THEOREM 5.6.– A wff for FOL F is satisfiable iff it is satisfiable on the domain H (sk(F)).

PROOF.– If:

– We consider sk(F).

– F is satisfiable iff sk(F) is satisfiable (see section 5.5.2).

– By hypothesis, sk(F) is satisfiable on H(sk(F))% (see remark 5.20).

– Therefore, F is satisfiable.

Only

– If F is satisfiable, then F is satisfiable on denumerable domain D (Löwenheim-Skolem theorem, theorem 5.4).

– We repeat the reasoning of theorem 5.4, but instead of taking elements in D, we take the Herbrand terms that denote them to construct another denumerable set D'.

– D' = H(sk(F)).

The following theorem, which simply merges theorems 5.5 and 5.6, is essential for the automation of FOL.

THEOREM 5.7.– (Herbrand). A wff of FOL F is valid iff there exists a finite set of instances of sk(¬F) that is unsatisfiable (contradictory).

PROOF.–

– F is valid iff ¬F is unsatisfiable.

– ¬F is satisfiable iff ¬F is satisfiable (see section 5.5.2).

– sk(¬F) is unsatisfiable iff (sk(¬F)) is unsatisfiable % HI: Herbrand Instances.

 

(semantic definition of universally quantified formulas, see definition 5.6)

– If HI(sk(¬F)) is unsatisfiable then there exists a finite subset of HI(sk(¬F)) that is unsatisfiable, (up to a syntactic modification, HI are propositional, and we may apply the (contrapositive of) the compactness theorem for PL (theorem 3.3)).

It is clear that Herbrand’s theorem enables us to design a semi-decision procedure for FOL:

REMARK 5.21.– (completeness of FOL). Gödel’s completeness theorem¹⁶ for FOL can be stated as follows: there exists a formal system in which every valid FOL formula has a proof.

The following is a formal system for FOL.

with:

: see definition 5.1

: the inference rule schema M P from ₁ together with the inference rule schemas G and P below:

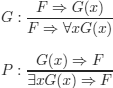
₁: the axiom schemas (A1), (A2), and (A3) of ₁ together with (A4) and (A5) below:

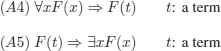
From a conceptual point of view, a formal system can be characterized as a “machine that produces (and tests) theorems in a given logic”, we can therefore view SEMI_DEC_PROC_FOL as a formal system for FOL and theorem 5.7 as a completeness theorem for FOL.

This theorem enables us to replace a test of validity on all interpretations (semantical notion) by a test of the existence of a proof (syntactical notion of a proof).

REMARK 5.22.– (very, very long proofs). To illustrate the idea, consider _FOL from remark 5.21, but the property below holds for all systems for which ? is undecidable (immediate by analyzing the proof).

Property:

The length of a theorem T, denoted by length(T), is the number of symbols (from the vocabulary of the corresponding formal system) in its statement. Similarly, the length of a proof is the number of symbols in the proof (other definitions can be given such as number of steps, etc.).

For any recursive function (i.e. computable by an algorithm) f, there exist a wff T of FOL such that , with such that the shortest proof of T has at least length f(n).

PROOF.–

– Assume that this property does not hold.

– There therefore exists a recursive function F for which every theorem T of length n has a proof of length at most F(n).

– It thus suffices to enumerate the finite set of all sequences of length, at most F(n) constructed on a finite vocabulary to identify a proof of T.

– This would be a decision procedure enabling us to decide whether a wff is a theorem of _L1O. Such a procedure cannot exist and we obtain a contradiction.

– Note that there exist theorems in _L1O of length, say, N, such that their shortest proofs are of length 10^100×N, for example.

It is natural to wonder whether there is a compactness theorem for FOL.

The answer is the topic of the next theorem.

THEOREM 5.8.– (compactness of FOL).

S : set of wffs of FOL.

If every finite subset of S is satisfiable, then S is satisfiable.

PROOF.–

– If S is finite, the proof is trivial, as S is satisfiable by hypothesis.

– (see remark 5.2).

– If a set of formulas is satisfiable, then so are all its formulas (Warning! The converse is not true, as all the formulas in a set have to be true in the same interpretation for a set of formulas to be satisfiable).

– Instead of S, we can consider (see section 5.5.2).

– It is sufficient to consider H(sk(F_i)) as a domain to test satisfiability (see theorem 5.6).

– We enumerate the (increasing) finite sets of closed instances (i.e. propositional) of:

S₁ = {sk(F₁)}, S₂ = {sk(F₁), sk(F₂)}, …, S_n {sk(F₁), sk(F₂),…,sk(F_n)},…

– As each formula involves a finite number of symbols, the sets of propositional formulas are finite; thus, by hypothesis (and theorem 5.6), is satisfiable.

– By applying the compactness theorem for PL, we conclude that is satisfiable.

– By applying theorem 5.6, we conclude that S is satisfiable.

5.6. Semantic trees in FOL

A “natural” way of implementing procedure SEMI_DEC_PROC_FOL is to use semantic trees.

REMARK 5.23.– We do not have to restrict ourselves to formulas in clausal form, but the method can be applied to formulas in Skolem normal form, i.e. that are universally quantified (see definition 5.10 and remark 3.31).

The method of semantic trees for FOL is the same as that for PL, by considering literals on the Herbrand base B(S).

Indeed, by considering, for example, the set of formulas from example 5.18 and the universe H(S):

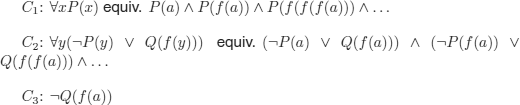
To produce a counter model of S, it is sufficient to give a Herbrand interpretation that is a counter model of a closed instance of a formula (i.e. of a conjunct on the right-hand side of “equiv.”).

The following example uses the method of semantic trees to show that the set of formulas S of example 5.18 is unsatisfiable.

EXAMPLE 5.20.–

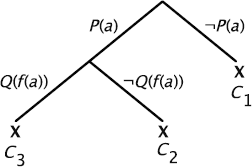
where C_i (1 ≤ i ≤ 3) under × means: this interpretation falsifies a closed instance of formula C_i.

The leftmost branch in the tree corresponds to the first Herbrand interpretation of S given in example 5.18.

Of course, the tree that is constructed depends on the enumeration order of B(S).

Just as for resolution in PL, the resolution rule in FOL applies to sets of clauses. It is therefore necessary to define clauses in FOL.

DEFINITION 5.10.– (FOL clause, clausal form).

A clause is a wff of the form:

where:

(i.e. all the variables in P are universally quantified)

Clauses are usually denoted:

(variables are implicitly quantified universally)

L_i: literal, i.e. of the form:

A formula is in clausal form iff it is of theform , where the C_i’s are clauses.

More frequently, as it was the case in PL (see remark 3.33), we will mention sets of clauses (or the set of clauses corresponding to a formula) S = {C₁,…, C_n}, and we will say that clauses are sets of literals.

If and are different clauses, then we always have (possibly after a renaming of the variables).

The clausal form of a wff F can be obtained from sk(F) and the rules on logical connectives.

5.6.1. Skolemization and clausal form

Skolemization can make things complicated. Some preprocessing can sometimes be useful.

1)

yields by Skolemization:

1')

(1') generates an infinite Herbrand universe

but (1) is equivalent to:

(see exercise 5.3 h)) and rename )

and after Skolemization we obtain the clause:

which generates a finite Herbrand universe;

and sometimes preprocessing makes matters worse.

2)

yields by Skolemization:

This clause generates a Herbrand universe containing one constant;

but (2) is equivalent to:

which, by Skolemization, yields:

2') P(a) ∨ Q(b)

(2') generates a Herbrand universe containing two constants.

Sometimes it can “hide” information:

the formula:

is obviously a tautology. Skolemizing this formula yields:

and we obtain ,

which is equivalent to:

3)

clause (3) will needlessly increase the size of the search space.

It can also increase the size of the problem specification. For the following formula:

the standard clausal form transformation yields 1,600 clauses!

REMARK 5.24.– The notion of Skolemization is related to the one used in the proof-as-programs approach, in which an algorithm is extracted from a constructive proof of a program specification.

The intuitionistic version of Church’s thesis¹⁷ goes as follows: if Ar is a first-order predicate of arithmetic, and , then there exists an algorithm f such that .

Herbrand’s theorem and the procedure SEMI_DEC_PROC_FOL enable us to obtain the following theorems as immediate corollaries.

THEOREM 5.9.– A set of clauses S is unsatisfiable iff for any semantic tree associated to S there exists a semantic tree that is closed and finite.

THEOREM 5.10.– (Herbrand’s theorem (for clauses)). A set of clauses S is unsatisfiable iff there exists a finite set of Herbrand instances of S that is unsatisfiable.

5.7. The resolution method in FOL

One may wonder whether the resolution rule also applies in FOL. The answer is yes.

In a famous paper from 1965, J.A. Robinson combined the resolution rule for PL with the unification algorithm, which led to a calculus with a unique rule permitting us to automate FOL.

This rule is defined as follows.

DEFINITION 5.11.– (resolution rule for FOL).

If σ is the mgu of .

This means that the resolvent clause is obtained by unifying all literals , and , then applying the rule as in the propositional case.

 

In practical implementations, the rule above is replaced by binary resolution (i.e. p = q = 1, we select two complementary literals, one in each clause) and a factorization rule that aims at unifying two literals with the same predicate symbols and the same sign that occur in a same clause.

DEFINITION 5.12.– (binary resolution rule for FOL). Given two clauses:

where:

, : disjunctions of literals.

If the system of equations:

has mgu σ as a solution.

The binary resolution rule between C₁ and C₂ is defined by:

Applying a substitution a to an n-tuple of terms is defined as follows:

Applying a substitution a to a clause is defined as follows:

We will note or simply (when there is no ambiguity). C is called the resolvent. C₁ and C₂ the parent clauses

DEFINITION 5.13.– (factorization). The restriction to two complementary literals causes the loss of completeness. To recover completeness, we need to add the so-called factorization rule which, starting with clause:

with : disjunction of literals (that may contain other literals of the form and and unifiable, generates:

where σ is the mgu of and

D is called factor of C.

A clause can have several factors.

EXAMPLE 5.21.– (the need for factorization to retain completeness). The set of clauses {P(x) ∨ P(y), ¬P(z) ∨ ¬P(u)} is unsatisfiable, but binary resolution generates infinitely many clauses of the form

without generating.

However, the factorization rule generates P(x) and ¬P(z), and the binary resolution rule generates.

DEFINITION 5.14.–

– Given a clause C, a copy or variant of C is a clause in which all variables of C have been renamed by fresh variables.

– A clause C is self-resolving iff the resolution rule can be applied on C and a copy of C. One such example is clause 2 of example 5.22.

EXERCISE 5.7.– (soundness of binary resolution). Use the method of semantic tableaux to prove that the binary resolution rule for FOL is correct (i.e. that every model of the parent clauses is a model of the resolvent).

REMARK 5.25.– (unsatisfiability and satisfiability by resolution). Each branch in a semantic tree (see section 5.6) denotes a partial interpretation of the set of clauses S; if S is unsatisfiable, then all the branches will falsify an instance of at least one clause in S (closed tree). By “unfolding” the closed tree (see the correction of exercise 3.34), we can obtain a refutation by resolution of a set of Herbrand instances of S. The proof is completed by using the so-called “lifting lemma” that enables us to relate closed instantiated clauses (i.e. propositional clauses) and those that are not instantiated. in other words, the following diagram commutes:

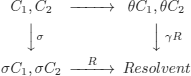
where σ, θ, ρ, and γ denote substitutions (σ and γ are closed substitutions) and the operation that yields the resolvent of two clauses.

Soundness and (a consequence of) refutational completeness are often presented using operator (see also definition 3.16):

Let S denote a (finite) set of FOL clauses.

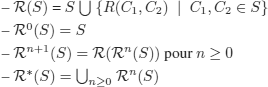
*(S) denotes the search space, of which all strategies try to explore the smallest subset.

Thus,

– if , then S unsatisfiable.

– if and , then S satisfiable.

– else (FOL undecidable)? (This alternative is impossible in PL).

EXAMPLE 5.22.– Consider the clauses 1, 2, and 3 below. We indicate an application of the resolution rule by specifying, as for PL, the selected clauses and literals, together with the unifier.

1) P(a)

2)

3)

4)

EXAMPLE 5.23.– (what should not be done). We may wonder why it is necessary to apply the method strictly if “we can see” the replacements that can be done to apply the resolution rule for PL, in other words, whether we can get rid of unification:

1) P(a)

2)

3)

4)

5)

This way of proceeding is correct from a logical point of view (variables in clauses are universally quantified and can be replaced by any constant), but it is incorrect if you are asked to apply the resolution rule in FOL.

Furthermore, it neglects the most original and powerful characteristic of the resolution rule: the presence of the unification algorithm.

Perhaps, you can convince yourselves by trying to “see” what replacements should be performed to apply resolution between clauses 2 and 3 below:

1) P(a)

2)

3)

EXAMPLE 5.24.– (grandparents).

Every human has a parent:

i)

The parent of a parent is a grandparent:

ii)

Every human has a grandparent:

iii)

We want to use the resolution rule to show that (iii) is a logical consequence of (i) and (ii). We therefore negate and Skolemize . It is also necessary to Skolemize (i).

We consider the set of clauses 1, 2, 3 below.

1) P(f(x),x)

2)

3)

and we provide a refutation for this set:

4)

% formally speaking, the unifier is , but as the couple x ← v is not useful in what follows, it is not included.

5)

6)

EXAMPLE 5.25.– (natural numbers). The following set of clauses translates the statement 0 is a natural number and if x is a natural number, then so is the successor of x:

We want to use the resolution rule to show that 3 is a natural number. We therefore add the following clause to the two previous ones:

and we try to derive.

a) Backward chaining:

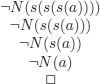
b) Forward chaining:

EXAMPLE 5.26.– (first negate and then Skolemize). Consider the following reasoning, formalized in FOL:

Can you prove that this reasoning is correct (or incorrect)?

To prove that the reasoning is correct (or incorrect)

using the resolution method

Mr (or Mrs) A proposes:

Skolemize the conclusion, then negate the result, which leads, say, to formula (3'), and then try to prove the unsatisfiability of the set of clauses obtained from (1), (2), and (3')

and

Mr (or Mrs) B proposes:

Negate the conclusion, then Skolemize the result, which leads, say, to formula (3''), and then try to prove the unsatisfiability of the set of clauses obtained from (1), (2), and (3'').

Who is right?

a) Mr (or Mrs) A

b) Mr (or Mrs) B

c) Both of them

d) None of them

i) We use the method proposed by Mr (or Mrs) A

The set of clauses to refute is thus 1. to 3.:

1)

2)

3)

4)

5)

The resolution rule can no longer be applied; hence {1., 2., 3.} is sat and as a consequence, the reasoning is incorrect (according to Mr. (or Mrs) A)

ii) We use the method proposed by Mr (or Mrs) B

The set of clauses to refute is thus 1. to 3.:

1)

2)

3)

4)

5)

We have proved that the set of clauses {1., 2., 3.} is unsat, and as a consequence, the reasoning is correct (according to Mr (or Mrs) B)

Mr (or Mrs) B is right.

Why is that?

Proof in natural language

Q denotes a total relation (1.), i.e. for any object x, there exists an object y that is related to x in Q. Two objects that are in the relation denoted by Q are also in the relation denoted by P (2.). Hence, for any object x, there exists an object y that is related to x in P.

Formal proof (semantic tableaux)

We consider the set of formulas {∀x∃yQ(x, y), ∀x∀y.Q(x, y) ⇒ P(x, y), ∃x∀y¬P(x, y)}

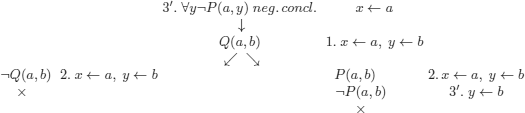
Explanation

If formula Q is a logical consequence of formula P, then the relationship between their models is:

But as Skolemization can lead to the “loss of models”, after it is performed, we may get the following relationship between the models of the premises (P) and the conclusion (Q).

The shadowed zone in P corresponds to the counter examples.

EXERCISE 5.8.– Use the resolution method to prove that the following reasoning is correct.

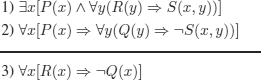
EXAMPLE 5.27.– Consider the set of clauses 1 to 7 below.

We show that this set is unsatisfiable by using a unit strategy (at least one of the parents is a unit clause). The underlying idea is that the obtained resolvent contains strictly less literals than the non-unit parent clause, and the rule thus generates clauses that are potential candidates for the generation of.

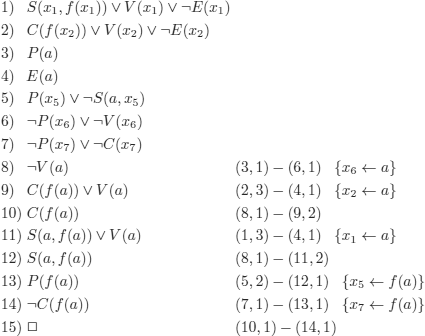
EXAMPLE 5.28.– (a theorem in group theory). We use the resolution rule to show that every element of a group has a right inverse.

Clauses 1 to 6 below are the clausal form of the set of axioms that define a group and of the negation of the conclusion.

We apply a backward chaining strategy, meaning that we begin by applying the resolution rule with the negation of the conclusion as one of the parent clauses, and we proceed with a linear strategy, meaning that one of the parent clauses is always the last clause obtained.

This is very close to what a human would do: conclusions (lemmas) do not need to be memorized for future usage.

Similar to what a program would do, we have systematically renamed variables to avoid any confusion.

A linear strategy is often represented graphically as follows:

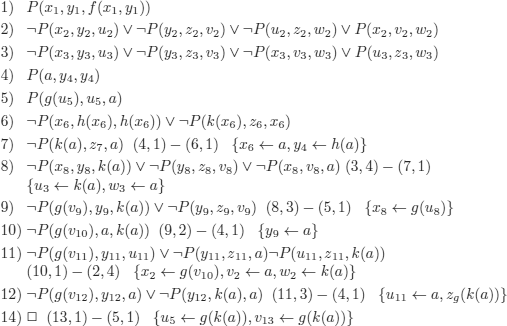
EXAMPLE 5.29.– (the monkey and the banana). A monkey wants to eat a banana that is hanging from the ceiling of a room. The monkey is too small to reach the banana. However, the monkey can walk in the room, carry a chair that is in the room, climb on the chair and take the banana to eat it.

We want to describe this situation with a set of clauses. Functional terms can be used to denote actions.

The question will be: does there exist a state that is reachable from a given initial state, where the monkey can catch the banana?

In order to solve this problem using resolution, we choose the following particularly simple formalization (set of Horn clauses, see section 3.9).

P(x, y, z, s): in state s, the monkey is at position x, the banana at position y, and the chair at position z.

R(s): in state s, the monkey can reach the banana.

f(x, y, s): the state that is reached from state s, if the monkey walks from x to y.

h(s): the state reached if the monkey is in state s and climbs on the chair.

P(a, b, c, d): the initial state.

The corresponding set of clauses is:

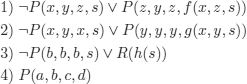
The question is , which will be negated to try to derive , thus yielding the clause.

Sometimes, the question is Answer(u) to explicitly retrieve the answer (see solution to exercise 5.9).

EXERCISE 5.9.– Find the solution to the problem of the monkey and the banana by applying the resolution rule and a linear strategy.

EXERCISE 5.10.–

a) prove by resolution that the set of clauses below is unsatisfiable:

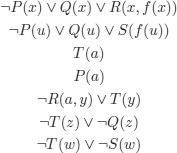
b) consider the set of clauses below:

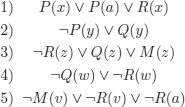
Is it possible to prove by resolution:

i) that it is unsatisfiable?

ii) that it is satisfiable?

iii) we cannot say anything?

5.7.1. Variables must be renamed

The clause is equivalent on the Herbrand universe (see definition 5.9) on to

{P(a) ∨ Q(b), P(f (a)) ∨ Q(f (f (b))),….}

But if we want to discover the instances of interest by unification, it is better to write:

with

(the i correspond to substitutions that would be computed by the resolution rule)

EXAMPLE 5.30.- We prove by resolution that the set of clauses 1,2,3 below is unsatisfiable:

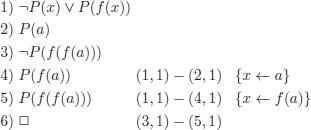
If variables are not renamed in 1, the contradiction cannot be proved (we would have assimilated with , i.e. usable only once).

EXERCISE 5.11.- Is the wff a logical consequence of With symbols:

As usual, x and y denote variables and P a predicate symbol.

Answer using the resolution method.

EXERCISE 5.12.– (S₁ and resolution). We have already appreciated the general difficulty of finding a proof in a formal system (for example, S₁). Hence, the idea of trying to do this work automatically by using, for example, the resolution rule.

You are asked:

i) To encode as clauses A1, A2, A3, and MP (see section 3.4) and to prove, using the resolution rule, that:

ii) To rephrase (as you would, for example, to explain it to someone who does not know the resolution rule) this proof.

Hint: encode by i(x,y) and use predicate symbol P with the meaning P(x): x is provable in ₁.

5.8. A decidable class: the monadic class

FOL is undecidable (but semi-decidable). Finding classes or fragments (i.e. sets of cwffs that are proper subsets of ₁ and that are decidable is one of the most important problems of logic, which is known as the “classical decision problem (for FOL)”. It can be presented in different ways.

Given F ₁, the problem of:

– satisfiability (coherence, consistency): decide if F is satisfiable;

– validity: decide if F is valid;

– provability: given a formal system that is correct and complete, decide whether F.

The interest of being able to characterize such classes (or fragments) is clear: trying to have a “good” expressive power, while retaining “very good” decidability properties.

In this section, we shall prove the decidability of some fragments of FOL. We begin by some definitions.

DEFINITION 5.15.– (finitely controllable class, finite model property). A class is finitely controllable or has the finite model property iff for all F ∈ , if F is satisfiable, then F admits a finite model.

REMARK 5.26.– Every finitely controllable class is decidable. The converse is not true: there are decidable classes that do not have the finite model property.

Among the finitely controllable class, we shall study monadic logic.

DEFINITION 5.16.– (monadic class of FOL). The set of cwffs of ₁ containing exclusively unary predicates (and possibly =), but not containing any functional symbols (in particular, constants) is called the monadic class of FOL (or monadic FOL), denoted by MFOL⁼.

If the cwffs do not contain the equality symbol =, then we have the pure monadic class, denoted by MFOL.

MFOL was used to formalize Aristotle’s syllogistic. See also digression 8.1.

The proof of the decidability of MFOL⁼ is based on the following remarks:

1) To test the satisfiability of a wff of FOL (see definition 5.6), what matters is the cardinality of the domain of discourse D of the potential model (the definition of satisfiability does not take the names of the elements of D into account);

2) On a finite domain, say is equivalent to and is equivalent to .

3) Key point: (theorem 5.11): proving that MFOL⁼ is finitely controllable by providing an upper bound on the cardinality of the domains on which it suffices to test the satisfiability of the formulas in the class.

4) On a finite domain, we can consider all possible evaluations of unary predicates (and equality between variables) and use property 2 above. There are therefore only a finite number of interpretations to test.

The following theorem proves to be the key property of the decision procedure for MFOL⁼.

THEOREM 5.11.– (MFOL⁼ has the finite model property). A cwff F of MFOL⁼ containing k predicate symbols and v variables is satisfiable (on a structure iff F is satisfiable on a structure

PROOF.– (detailed outline).

if:

Trivial: if a wff is satisfiable on a domain of a given cardinality, then it is satisfiable.

only if:

Define relation R on D:

for ₁, ₂ D

₁ R ₂ iff:

and and … and

where the denote the k predicates in F and, as usual, (j = 1, 2) T or F depending on whether P_i is evaluated to T or F on a_j.

If we were to rigorously stick to definition 5.6, we would have to say that a₁, a₂ are in relation R if and only if they belong (or do not belong) to the relation assigned by the interpretation (model) to , i.e.

% The idea is that the elements of D on which the predicates are evaluated to the same truth value are regrouped.

R is an equivalence relation (see definition 3.26).

The proof is trivial and is a result of the properties of equality (see also section 9.1.4):

– reflexive a₁ R a₁, as ;

– symmetric: if a₁ R a₂ then a₂ R a₁, as if , then .

– transitive: if a₁ R a₂ and a₂ R a₃, then a₁ R a₃, as if and , then .

As there are two possibilities for each P_i (for any _j), there are 2^k equivalence classes.

If we now consider the equalities, that can only relate the v variables (see definition 5.16), it is sufficient, for each equivalence class, to consider at most ₁, ₂,…,_v elements (_i ∈ D; . If the equivalence class contains p(p<v) elements, we consider a₁, a₂,…, a_p.

We thus consider:

: with

i.e. card.

We define the relations in':

iff , where [a] is (a representative of) the equivalence class of a (a ∈ D).

% Recall that equivalence classes of D form a partition of D.

By structural induction (see section 5.2.3) and using properties 1 to 4 of section

5.8, we prove:

.

REMARK 5.27.– (syllogistic and decidability). Aristotelian syllogisms can be formalized in MFOL (see remark 2.7). As this is a decidable fragment of FOL and as the latter is undecidable, syllogistic is not sufficient to reason in FOL.

EXAMPLE 5.31.– (see also example 5.11).

Here, k = 1; v = 1; hence, it suffices to test

Indeed, we consider F, and on D_max, we can obtain the models of F (i.e. counter examples of F): . Hence, F is not valid.

EXAMPLE 5.32.– (some cwffs in the monadic class). We have treated some of those by the method of semantic tableaux in example 5.13, exercise 5.3 (a)-(b)-(h)-(k2), and exercise 5.4.

Note that, in general, we can detect (non)-validity on universes of a lesser cardinality than the upper bound of theorem 5.11.

5.8.1. Some decidable classes

There exist techniques other than the one we used to solve the classical decision problem for MFOL⁼. These techniques are beyond the scope of this work.

The decidable fragments of FOL are characterized by the prefixes of the prenex normal form that is equivalent to the cwff that is provided as an input (see theorem 5.3).

– Bernays-Schönfinkel: (also denoted by ; M in MFOL);

– Ackermann: (also denoted by );

– Herbrand: arbitrary prefix and matrix with L_i (1 ≤ i ≤n): literals;

– Gödel-Kalmar-Schütte: (also denoted by ;

– with and L_i (1 ≤ i ≤ n): disjunction of literals with at most one positive literal.

5.9. Limits: Gödel’s (first) incompleteness theorem

A particularly simple proof of this capital theorem (given by G. Boolos) uses the following notions: paradox, arithmetic, truth, proof, algorithm and encoding.

Paradox

Here it will be the Berry’s paradox, see example 2.1.

Arithmetic

See example 3.8.

Truth

See section 5.2.1.

Proof

See section 3.3.

Algorithm

Informally, an algorithm is any well-defined computation procedure that admits a (set of) value(s) as an input and produces a (set of) value(s) as an output. Examples are a program (in a programming language), a Turing machine, Markov algorithms, formal systems for arithmetic, etc.

Encoding (in arithmetic)

Encoding a text consists in replacing a word or sentence by another word, a number or a symbol. In cryptography, a code uses the substitution at the word level, whereas a cipher uses the substitution at the level of letters. The goal is to hide information.

We shall use a translation that associates to every wff of a given language an integer (i.e. a word in arithmetic). The goal is not to hide information but to change its representation.

Arithmetic enables us to uniquely encode into a natural number any sequence of symbols (i.e. a string on a vocabulary), for example, a wff in ₁, instructions of a Turing machine (or of a program), a computation of a Turing machine (as it can be described as a sequence of instantaneous descriptions of the Turing machine), proofs in a formal system, etc.

The first to propose an encoding was K. Gödel (in 1931), the natural number encoding an expression M has since been known as the Gödel number of M, denoted by gn(M).

DEFINITION 5.17.– Let M denote an expression (a word) on a vocabulary V.

We assign to each symbol in V an odd number (> 1):

Given the expression

the Gödel number of M is the natural number:

where Prime(k) is the k^th prime number.

If M = є (i.e. the empty string), then ng(є) = 1.

For example, for a string

Why this encoding? The justification is immediate if we recall the fundamental theorem of arithmetic (see below).

THEOREM 5.12.– (fundamental theorem of arithmetic). Every x (x > 1) can be represented as

with : prime and .

This representation is unique (up to the commutativity of ×).

An immediate corollary is:

COROLLARY 5.2.– (uniqueness of the encoding of words). If ng(M) = ng(N), then M = N.

DEFINITION 5.18.– (Gödel number of sequences of words). Let : M₁M₂…M_n denote a finite sequence of expressions (i.e. words on a vocabulary), the Gödel number of is defined as:

An immediate corollary is the following:

COROLLARY 5.3.– (uniqueness of the encoding of sequences of words). If ng(₁) = ng(₂),then ₁ =₂.

REMARK 5.28.– (other encodings). A word or a sequence of words has a unique gn, but a set of n words (expressions) has n! possible gn. We will always consider sequences of words, as they each have a unique gn.

Other encodings are possible (and used), for example, the encoding of n-tuples, which is used in the proof of theorem 5.5. They are also called Gödel numbers.

We give a version of Gödel’s famous theorem that is particularly interesting in computer science.

THEOREM 5.13.– (Gödel’s first incompleteness theorem). There is no algorithm that can produce all true cwffs of arithmetic (i.e. without there being any false cwff in the list).

PROOF.– A sensible observation about this theorem is that if such an algorithm were to exist, in order to know whether a conjecture Conj holds or not in arithmetic, it would suffice to “sit and wait” for Conj or ¬Conj to be added to the list.

Proof technique: we assume that such an algorithm m exists and we construct a cwff that is true in arithmetic but is not in the output of M.

If n , we will write

where s denotes the successor function and 0 denotes itself. % For example, 4 : ssss0.

– We will say that a formula F(x) designates n if the formula occurs in the output of M.

For example, if in the output of M we find

then formula x + x = ssss0 designates the integer 2.

– Names are unique: imagine that this is not the case, for example, if the following cwffs occur in the output of M:

1)

2)

then, after replacing F(x) in (2) by the name it designates in (1) we obtain:

– If the number of symbols in our formalization of arithmetic is A (if there are infinitely many variables, they can be generated, e.g. by x and {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, x₀, x₁, x₂, x₃,…) there are at most Aⁱ formulas containing i symbols.

For any m , there are therefore finitely many numbers that are designated by formulas with at most m symbols. Thus, there are integers that are not designated by formulas of at most m symbols. Hence, there exists a least one integer that is not designated by such a formula (we order finitely many designated numbers and take the successor of the greatest designated number).

– We construct a formula C(x, y) meaning “x is a number that is designated by a formula containing z symbols”:

length being, for example, the program from example 6.17 feeding it as an input:

.

We could of course have used any other program that computes the length of a list¹⁸.

– Let B(x, y) denote the formula with the intended meaning: “x is designated by a formula containing less than y symbols”:

< is definable in arithmetic: .

– Let A(x, y) denote the formula with the intended meaning: “x is the smallest number that is not designated by a formula containing less than y symbols”:

– Let k denote the number of symbols in A'(x, y). Of course (by inspection), k > 3 and let F(x) denote the formula with the intended meaning “x is the smallest number that cannot be named by a formula containing less than 10 × k symbols”:

Let us see how many symbols F(x) contains:

symbols

F(x) also contains the symbols , y, (, y, x, =,), Λ,) 10 symbols

F(x) thus contains a total of k + 22 symbols and as k > 3, k + 22 < 10 × k, thus F(x) contains less than 10 × k symbols.

– As mentioned above, there exists a smallest number among those that are not designated by a formula containing less than m symbols.

Let n be this number for m = 10 × k.

n is not designated by F(x), i.e.

is not among the outputs of M.

But (*) is a cwff that is true, as n is the smallest number that is not designated by a formula containing less than 10 × k symbols.

REMARK 5.29.– (incompleteness theorem and constructive mathematics). The notion of a proof is essential in constructive mathematics, as it is used to explain the meaning of existence.

From a constructivist point of view, to say that a proposition is true is equivalent to saying that we can find a proof of . Some authors call this identity the “To assert is to prove” principle:

A-P: (p is a proof of )

The following problem arises naturally: how can Tarski and Gödel’s results be reconciled with the principles on which constructivism is founded? In other words: what are these truths that cannot be proved (as according to A-P, truth coincides with proof)? The answer is that constructivists do not limit themselves to proofs in formal systems, but principle A-P refers to proofs that are correct from a constructivist point of view, knowing that provable means provable by any sound means and not provable in a given formal system.

There are therefore arithmetic truths that cannot be proved in a formal system, but that can be proved by correct means from a constructivist point of view.

---

1 It is interesting to note that in mathematics, a large majority of relations, denoted using predicates, are binary.

2 The expressive power of a logic depends on the objects that it permits us to consider (along with the possibility or not of quantifying these objects). The expressive power is obviously related to the properties of the logic itself ((un)decidability, etc.). See also section 9.3.

3 w is a substring of v iff there exist strings x, y (possibly empty) such that v = xwy.

4 Thus, if it contains occurrences of ¬, they are “next” to the atoms.

5 See also digressions 3.3 and 9.1.

6 In the Western world, since Parmenides and Aristotle.

7 The notion of truth is closely related to that of negation by the equation false = not true.

8 This is not the case, for example, with the statement “my head hurts”.

9 A closed statement is satisfied either by all assignments or by none, depending on whether it is true or false.

10 According to our definition, this is actually not a formal system: a formal language and formal inference rules are missing, but the context is clear enough and there is no ambiguity.

11 For example, the expression Let x denote a prime number translates into .

12 If any two models of a theory are isomorphic, then the theory is categorical.

13 Irreflexive non reflexive .

14 Another possibility of automation is the use of heuristics, but in this case, we cannot guarantee that the procedure will halt with a correct answer in all the cases in which the formula has the expected property.

15 I.e. specify uncountably infinite sets and none other.

16 Should not be confused with Gödel’s incompleteness theorem, which is much more popular (see remark 3.28 and section 5.9).

17 Its classical version: a function is computable iff it is intuitively computable.

18 A program can be viewed as a sequence of instructions, each instruction can have a unique code, and the encoding of theorem 5.5 enables us to assign a unique natural number to a program.