Chapter 10
Non-Classical Logics
In the following sections, we shall present some of these logics. The study can be partially based on the notions that were introduced in the previous chapters.
As usual, the presentation will contain motivations, historic landmarks, applications, similarities, and differences with what is already known, and finally indications on how to reason with these logics.
A common feature of these logics is their philosophical origin, which can be explained as a return to the roots: analysis of discourse in natural language, of what is true, what is false, what is neither true nor false, what is necessary, what is contingent, etc.
10.1. Many-valued logics
One of the first conventions that we adopted in the study of logic was to state (in accordance with mathematics) that a reasoning is correct if and only if it is impossible for the premises to be true and the conclusion to be false. But common sense shows that things are not that simple, when we want to begin the analysis before any simplification choice has been made.
Indeed, among the syntactically correct sentences, those we are interested in are declarative sentences and more precisely propositions (i.e. the sets of declarative sentences that are synonyms).
There are declarative sentences that are never assigned truth values, for example,
Honesty is beautiful
whose meaning can only be metaphorical. Others such as
The robot is in the room
can sometimes be true and sometimes be false...
The study of many-valued logics, which we shall also refer to as p-valued logics or n-valued logics (implicitly stating that p, n ≥ 3), originated, similar to many other subjects, with the work of Aristotle, who considered the future contingents (see section 10.3), i.e. what may or may not occur. The example considered by Aristotle was the proposition:
There will be a sea battle tomorrow.
which is neither true nor false (today) and suggests a third truth value. Łukasiewicz (following Aristotle) believed that if we do not accept that declarative sentences about the future are neither true nor false, then we have to accept fatalism (philosophical doctrine according to which all events are predetermined by fate).
Some historic landmarks:
– during the Middle Ages, little research on the topic;
– end of the 19th Century and beginning of the 20th Century: they are definitively accepted;
– some important names: MacColl, C.S. Peirce (around 1909), N.A. Vasil’ev, Łukasiewicz (starting in 1920), and Post (starting in 1921);
– three-valued logics have been particularly studied;
– there exist ∞-valued logics (infinitely-valued logics), in particular, the 
logic (see section 10.2).
The introduction by Łukasiewicz of p-valued logics was preceded by some profound philosophical considerations.
According to historians and philosophers of logic, two principal origins of p-valued logics seem to have been:
1) the theory of contradictory objects, that states the existence of objects having contradictory properties. It seems like Łukasiewicz believed that non-contradictory objects did not exist;
2) (for three-valued logic) the notions of (non)determinism, causality, free will, etc.
Łukasiewicz studied the problems of induction and probabilities seriously. In his first papers, the logical values depended on the finite number of considered individuals, for example:
To x2 = 1, we assign value 2/3 in the universe {-1, 0, 1}
To x2 = 1, we assign value 2/5 in the universe {-2, -1, 0, 1, 2}
We reduce the algebraic formalizm to a minimum for the treatment of p-valued logics. The adopted formalization is sufficient for our needs and can easily be generalized.
Using logics with three truth values can cause the loss of powerful techniques such as the law of excluded middle. For example, the following reasoning:
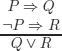
is not a correct reasoning in three-valued logic.
EXAMPLE 10.1.– A finer analysis of programs can be performed with a three-valued logic than with a two-valued one.
For example, if p and q are Boolean conditions and f and g are functions ((p → f, q → g, h) means: if p then f else (if q then g else h)):
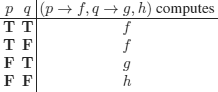
It seems obvious that the programs (p → f, f) (meaning if p then f else f) and f are equivalent; however, whereas f always computes f, we can imagine that, for example, p: (1/x) ≤ 3, and as variable x is real, it can take the value 0, which yields:
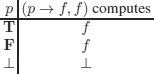
DEFINITION 10.1.– (truth functional (extensional) connective). A binary connective 
is truth functional iff the truth value of 
only depends on the truth values of 
and 
(i.e. a truth table can be provided for ). A logic is truth functional iff all its connectives are truth functional. Truth functional connectives are also called extensional connectives (see definition 2.3).
DEFINITION 10.2.– (n-valued logic). If 
is a formal language generated by propositional variables and connectives, N ⊂ N, N = 0, 1,…,n-1 is a finite set of truth values and D ⊆ N is a set of distinguished values, then L =<, N, D> is an n-valued logic.
We can take an infinite set for N (see definition 10.3).
REMARK 10.1.– One fundamental characteristic that is shared by classical and many- valued logics is truth functionality.
We shall present the most commonly used three-valued logics, that is, those of Łukasiewicz, Kleene, and Bochvar.
Łukasiewicz’s L3 logic (1920)
Basic principle: being able to handle contingent futures. To do so, he introduced the intermediate value 1/2.
The connectives are defined with the following tables:
the other usual connectives are defined as follows:
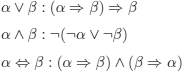
which yields:
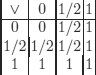
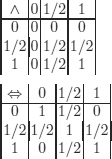
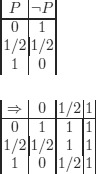
DEFINITION 10.3.– (interpretation, valuation).
– An interpretation (valuation) is an application: set of wffs → {0, 1/2, 1} that respects the truth tables above.
– A tautology or valid wff is a wff that takes the value denoted by 1 (or a value in D) for every interpretation.
For general p-valued logics, we must consider N instead of {0, 1/2, 1} and D instead of 1.
What changes and what does not:
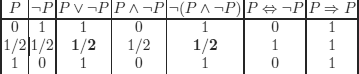
P ∨ ¬P: tautology in CPC (Classical Propositional Calculus), non-tautological in L3
¬(P ∧ ¬P): tautology in CPC, non-tautological in L3
P ⇔¬P: contradiction in CPC, satisfiable in L3
P 
P: tautology in CPC, tautology in L3
A formal system for this logic:
with:
3 = 0 % i.e. it is the same as for S1
= {MP}
:
3L1) 
3L2) 
3L3) 
3L4) 
REMARK 10.2.– In L3, the deduction theorem (see remark 3.14) does not hold.
The truth tables could have been established the following way:
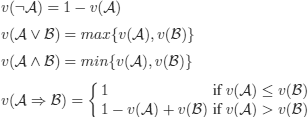
or
Sometimes, the latter is expressed as:
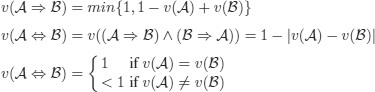
These last definitions naturally lead to considering n-valued logics with n ≥ 4, in particular ∞-valued logics.
Kleene’s three-valued logics (1938 and 1952)
Basic principle: give a value that means undecidable (and not an intermediate value) to the mathematical assertions that are true or false, but cannot be proved or refuted.
REMARK 10.3.– This principle is not respected by the laws of excluded middle and of non-contradiction. Doing otherwise would lead to the non-respect of truth functionality. For example, we would assign true to 
. Assume the value of p is 1/2 and that 
is replaced by 
q with the same truth value, then the value of 
is...1/2, because 
(table for ) and 
(table for ∨).
In so-called strong logic (1938) we assign the value i when the values 0 (false) and 1 (true) are not sufficient to conclude (same principle as in Łukasiewicz’s L3).
The other truth tables are the same as in L3.
In so-called weak logic (1952), the occurrence of value i in a sub-formula forces the formula to also have value i.
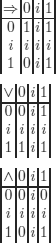
Bochvar’s three-valued logic (1938)
Basic principle: try to eliminate paradoxes, such as
This sentence is wrong.
(It is true if it is false, false if it is true)
Similarly to Kleene’s weak logic, if a sub-formula has value i, then the formula also has value i.
For Bochvar, a proposition can be significant (it is true or false) or without signification (a paradox). He proposed two types of connectives: the internal connectives and the external connectives. The connectives we are interested in here are the former, whose truth tables coincide with Kleene’s weak connectives.
Paradoxes are not eliminated:
This sentence is false or undetermined.
(It is true if it is false or undetermined, it is false or undetermined if it is true.)
10.1.1. How to reason with p-valued logics?
We show in the following example how to extend the method of semantic tableaux for classical logic (see section 3.2), to handle p-valued logics (p: finite). The method is general of course, as will be evidenced by the example.
In classical logic (two-valued), the method of semantic tableaux enumerates all the models (partial models in FOL) of a finite set of formulas S. When it is not possible to construct any model, we conclude that S is unsatisfiable (see section 3.2).
10.1.1.1. Semantic tableaux for p-valued logics
We consider L =<, N, D> and a set of symbols that do not belong to the vocabulary of : a0, a1, a2,... an-1. These ai, 0 ≤ i ≤ n − 1 will be used to indicate the n truth values of the (sub-)formulas in the tableau.
We discover the new method by analogy with the analogy for two-valued logic.
two-valued logic:
1) We are interested in the interpretations v such that v(X) = 1 (i.e. true).
2) Branch B is closed iff P ∈ B and ¬P ∈ B for P (in X): atomic.
3) X is valid iff tableau closed for ¬X.
p-valued logics (p ≥ 3):
1) We are interested in the interpretations 
such that (X) ∈ D.
2) Branch B is closed iff either ai(P) ∈ B, aj(P) ∈ B for i ≠ j and P atomic or B contains a formula on which no rule can be applied.
3) X valid iff the tableau is closed for all aj(X) with j ∈ (N − D), meaning that X cannot be evaluated to a value that is not distinguished.
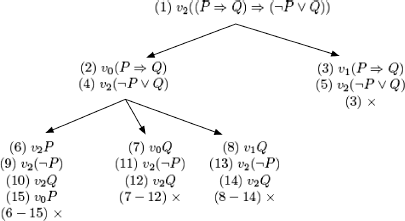
EXAMPLE 10.2.– (N. da Costa). In this example, we show how to adapt the method of semantic tableaux to p-valued logics. Although this is only an example, it is clear that the method can be applied for any finitely valued logic.
Given the following truth tables for connectives ¬, ∧, and ∨ in a three-valued logic, with distinguished values D = {0, 1}.
In each truth table, the leftmost column corresponds to all possible values of the argument on the left-hand side of the connective (named X below). The first line corresponds to all possible values for the argument on the right-hand side of the connective (named Y below).
We want to show that the following formula is valid:
We translate the truth tables (and try to compress their representation).
i(form) (0 ≤ i ≤ 2); form ∈ {X, ¬X,X Y,X ∨ Y,X ∧ Y} means form has value i.
(Although we do not need the connective ∧ in this example, we also provide the corresponding rules).
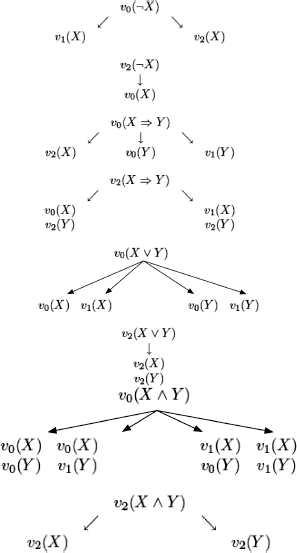
Method: show that it is impossible to evaluate the considered formula to a value that is not distinguished (in this example, value 2).
10.2. Inaccurate concepts: fuzzy logic
No man has ever or will ever know anything certain.
Xenophanes (6th Century BC)
Similar to the word “model” (see section 5.2), the word “concept” is very frequently used, for example, in AI (and sometimes, it is badly used). It is a notion that has been studied extensively in philosophy.
Among the technical definitions that can be found in the literature, we choose the following one:
Concept: an idea (of a mammal, a triangle, etc.) that is abstract, general, or can be subject to a generalization.
Concept is the rational way of knowing reality.
A distinction must be made between the concept and the object. The concept is the intensional counterpart1 of the object2.
There are a priori concepts, i.e. concepts that are not a result of experience, unity, plurality, etc. and a posteriori concepts, i.e. general notions that define classes of objects that are either given or constructed (concept of a mammal, a function, etc). Different philosophical schools claim that only one or the other of these concepts is really a concept.
Every concept possesses an extension, possibly empty. The objects are defined by the concepts that indicate the set of characters that belong (or are supposed to belong) to the objects of the class, and to no other object, for example, man: rational animal.
When creating concepts, similarity (analogy) plays a crucial role. We can also say that the notion of similarity (of which we could say that equality is a particular case3) also plays a major role in FL.
We can relate this notion to that of a model. In a model, we choose some characteristics that we wish to be representative and whose goal could be to define the class under consideration.
REMARK 10.4.– The activities of definition (specification) and modeling are at the core of a computer scientist’s activities. They can be viewed from the point of view of the philosophical classification of constructive definitions (specification) and explanatory definitions (modeling). Example of the former: append (see example 6.2) and of the latter small: someone of a size less than (say) 1.70 m.
Inaccurate concepts
A simple way of illustrating the ideas is to oppose mathematical concepts to empirical concepts. The former are exact because they do not accept limit or neutral cases (example: prime number, right triangle,…). The latter accept neutral cases and are inaccurate (example: big, old, etc.).
More generally, in natural languages, there are terms that are vague, i.e. terms (corresponding to concepts) such that if the extension of the concept is the class denoted by 
, and if we consider an arbitrary object denoted by 
, then there is no defined answer to the question: “is an object in class ?”. For example, very tall, small, bald, almost old, very beautiful, etc.
The vagueness is different from ambiguity (the same term can denote different objects in different contexts).
Mathematics and logic gave little consideration to vague concepts, more precisely, they use formal languages to avoid these difficulties.
The theory of fuzzy sets and FL (introduced by L. Zadeh in 1965) are an attempt to formalize vague or inaccurate concepts. Fuzzy sets and FL have given rise to many controversies.
Nowadays, the literature on these topics is huge and we may say that the domain is rather (an example of a vague term!) accepted and respected.
Fuzziness is inaccuracy and imprecision. The truth of a fuzzy proposition is a matter of degree. It must be distinguished from the probable (i.e. uncertainty as a degree of belief).
The following example clarifies the differences.
EXAMPLE 10.3.– Consider the following propositions:
a) John is young.
b) John will be alive next week.
a) is a vague or imprecise proposition (because of the occurrence of the word “young”).
b) is a precise proposition that is true or false, but we do not know that it is. It can be assigned a probability of being true or false, but the probability is not a degree of truth.
From an observational point of view, the vague concept “young” is in principle concerned with only one observation; however, the probability of a young person being alive next week is concerned with several observations of young people.
Most FL are truth functional (see section 10.1), which is not the case for probabilities:
we know that:
1) 
2) 
3) 
4) 
if for example:
(*) prob(p) = 1/2, hence prob(¬p) = 1/2
then using (3) with q : ¬p and replacing ¬p by p, which has, according to (*), the same probability, we obtain:
5) 
As a conclusion: in the left-hand side of (4), we replaced an event (¬p) by another event with the same probability (p) (see (*)) and we obtain two different values.
Another example (that also shows the difference with accurate propositions, in particular, the non-validity of the law of non-contradiction). From an intuitive point of view, the sentence:
I am old and I am not old.
does not have the value false. This can be formalized, because the basic logic for FL is 
(i.e. with values in 
), which gives 
, and which will in general will be ≠0.
Of course, 
.
The notion of FL has two meanings: a narrow sense and a wide sense.
For the narrow sense, FL is a logical system whose goal is to formalize approximate reasoning (see below the characterization proposed by L. Zadeh). In this sense, it is an extension of p-valued logics.
For the wide sense, FL ≈ theory of fuzzy sets.
A very old paradox seen from a new perspective. A good example of the kinds of problems that are treated by FL is the analysis (of an equivalent version) of the paradox of the heap (see example 8.1).
X denotes the set of all men
S ⊆ X the set of all small men.
We consider a real interval P = [0.5, 3] that contains all possible sizes.
The function size h : X → P.
We assume:
1) 
(meaning that there exist men who are small).
2) No man has a size less than 0.5 m or greater than 3 m (which yields interval P above).
3) There are men of all intermediate sizes - w.r.t. the minimal difference that can be detected by measuring instruments (this will entail no loss of generality in the reasoning).
4) If x ∈ S, y ∈ X, and 0 ≤ h(y) − h(x) ≤ 10−3, then y ∈ S (we could have chosen a smaller difference in size, e.g. 10-6.
A man that is 1 mm taller than a small man is also small.
5) If x ∈ S ∧ h(y) ≤ h(x), then y ∈ S. A man that is smaller than a small man is also small.
We want to prove that:
All men are small.
The proof is simple. Given any man y, we select a man, say x, who is without a doubt small. We choose x1 such that h(x1) − h(x) ≤ 10−3. By 4, x1 ∈ S.
By iterating (at most 103(h(y) - h(x)) times), we reach the conclusion that y is small. (If y had been smaller than x, by (5) we would immediately have reached the conclusion).
By applying (4), we prove that all men who are taller than a small man are small.
Where is the problem?
The idea to resolve this paradox is to represent the set S (i.e. the extension of the concept “small man” as a fuzzy set (see definition 10.4), i.e. a class of objects for which the transition from membership to non-membership is gradual rather than abrupt.
FL and fuzzy sets were introduced to take what is called practical reasoning into account, essentially to model those aspects that are hard to handle with classical logic. An example of practical reasoning is the frequent mix of precise and approximative reasoning that is performed when solving problems.
FL deals with fuzzy propositions such as: Patricia is extremely intelligent. Most dogs are nice. Michael is much taller than John, and so on.
One particular characteristic is that not only is the meaning of terms subjective, but it is also local, i.e. restricted to the considered domain of discourse (it is not really the same to be considered as tall by Pygmies or by Scandinavians). Thus, FL can be viewed as a logic whose propositions, connectives, truth values, etc. do not have a universal value. This implies that inference processes in FL are of a semantic nature rather than a syntactic one.
The creator of FL (L. Zadeh) described it as follows:
Perhaps the simplest way of characterising fuzzy logic is to say that it is a logic of approximate reasoning.
The term fuzzy logic is used to describe an imprecise logical system, FL, in which the truth-values are fuzzy subsets of the unit interval with linguistic labels such as true, false, not true, very true, quite true, not very true and not very false, etc.
Some examples are:
Fuzzy sets: definition and fundamental properties
DEFINITION 10.4.– Let U denote the universe of discourse.
A fuzzy set A is defined by the generalized characteristic function:
(the range of a standard characteristic function is {0, 1}, hence ordinary sets are considered as particular cases in the theory of fuzzy sets).
Interpretation: the values of 
A(x) are interpreted as degrees of membership of x to A (0 denotes non-membership, 1 denotes membership, and 1/2 could represent semi-membership).
EXAMPLE 10.5.– Consider the property “to be much greater than 1”, defined on +. It can be assigned to a fuzzy set A with A : + → [0, 1], where A is an arbitrary function that is continuous and non-decreasing such that, for example:
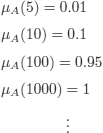
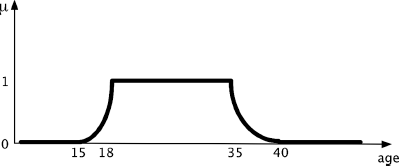
EXAMPLE 10.6.– The characteristic function of the set of people who can be professional football players could be:
The usual operations are (in general) defined as follows.
DEFINITION 10.5.– (set operations on fuzzy sets).
– A fuzzy set A is empty iff 
.
– Two fuzzy sets A and B are equal (denoted by A = B) iff 
.
– 
(if an element is somehow an element of A, then it must be an element of B in at least the same degree).
– 
(for all x, we shall thus write 
.
(for all x, we shall thus write 
.
– 
(for all x, we shall thus write 
.
EXERCISE 10.1.– (properties). Prove that if A, B, and C are fuzzy sets:
a) A ∪ B is the smallest set containing A and B.
b) A ∩ B is the biggest set contained in A and B.
c) A ∪ (B ∪ C) = (A ∪ B) ∪ C
d) A ∩ (B ∩ C) = (A ∩ B) ∩ C
e) 
f) 
g) C ∪ (A ∩ B) = (C ∪ A) ∩ (C ∪ b)
h) C ∩ (A ∪ B) = (C ∩ A) ∪ (C ∩ B)
DEFINITION 10.6.– A fuzzy n-ary relation in E is a fuzzy set in En.
EXERCISE 10.2.– Give the generalized characteristic function for the fuzzy relation in 
(i.e. (x, y) ∈ 2): x is much smaller than y.
EXERCISE 10.3.– (relations). The composition of two binary relations R and S, denoted by R o S, is defined as follows.
x(R o S)y iff ∃z such that xRz and zSy.
a) How would you define the composition of two fuzzy binary relations, i.e. what would the generalized characteristic function RoS be (as a function of R and S)?
How would you define the generalised characteristic function of a fuzzy relation R that is:
b) reflexive?
c) symmetric?
d) antisymmetric?
e) transitive?
The most commonly used basic logic for FL is Łukasiewicz’s 
(i.e. the set of truth values is the real interval [0, 1]). To the qualifiers true, very true, more or less true, neither true nor false, etc. fuzzy sets of the interval [0, 1] will be assigned. This choice is necessary to be able to manipulate the logic practically. In general, we are interested in a finite (small) number of truth values.
These ideas were formalized by L. Zadeh, with the concept of linguistic variables.
More precisely, a linguistic variable is a 5-tuple:
where:
– 
is the name of the variable (i.e. age, size, etc. from a qualitative point of view, by opposition to a quantitative point of view, with values 32 years, 1.75 m, etc.).
– 
is the set of linguistic variables (young, not young, very young, not very young, etc.).
– U is the universe of discourse (i.e. the set of values that the variable may take).
– G is the set of production rules that generate .
– M is the semantic rule.
where 
: set of parts of U, i.e. the set of all fuzzy subsets of U.
The idea behind the concept of linguistic variables is to obtain the fuzzy value of different terms as a function of those terms that were chosen as basic terms.
EXAMPLE 10.8.– (L. Zadeh). Linguistic variable: size
Basic term: small
= {small, not small, very small, very (not small), not very small, very very small, etc.}
is generated by the grammar (with axiom S):
S → A
S → not A
A → B
B → very B
B → (S)
B → small
If we assume that the generalized characteristic function (see definition 10.4) of the extension A of a concept is A, then in general, we take (other similar choices are of course possible):
graphical meaning:
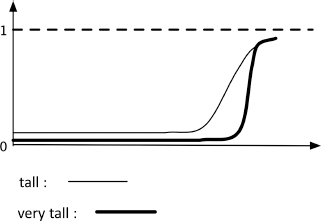
If the grammar had authorized it, we could have let, for example:
EXAMPLE 10.9.– (syntax and semantics). The symbols occurring in the rules on the right-hand side correspond to the fuzzy subsets of [0, 1]. Of course, indices l and r correspond to left and right (of a rule).
EXERCISE 10.4.– Does the grammar of example 10.9 permit us to generate the linguistic variable not very true and not very false? If so, compute its truth value.
Fuzzy sets permit us to obtain an elegant solution to the paradox4.
All men are small.
The only remark to be made is that not all generalized characteristic functions correspond to the common notion of “small”. We define:
for some function f: X → P, which, to represent the extension of the concept “small man” must be5:
1) continuous (our appreciation changes progressively);
2) monotonically decreasing;
3) f(h(x)) = 1 (or f(h(x)) ≈ 1), for those men that are certainly small;
4) f(h(x)) = 0 (or f(h(x)) ≈ 0) for those men that are certainly not small.
For example:
We define the fuzzy relation “smallness of y with respect to x”
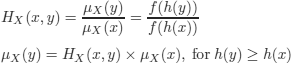
we assume there exists an x ∈ X such that X(x) = 1 (there is a man who is certainly small), for example, h(x) ≈ 0 (i.e. his height is almost zero).
Consider y ∈ X such that h(y) ≥ h(x), we may construct a finite sequence x = x0, x1, x2,… xN-1, xN = y and:
This formula translates the intuition that, as the process is iterated, the conviction that y is small disappears. Indeed, the product of the values in ]0, 1[ gets closer and closer to 0. The mathematical details are simple and are left to the reader.
REMARK 10.5.– We may see the origin of the paradox of small men (of the heap of grains, etc.) in the fact that each time a new man is considered, the memory that in general there were many men taller than someone small was lost. The treatment proposed above restores this memory.
10.2.1. Inference in FL
L. Zadeh proposed to treat the gradual membership of element x to a fuzzy set A by fixing values 
, 
; 0 < < < 1 and to use as a convention:
if A(x) ≤ , then x does not belong to A;
if 
, then x belongs to A;
if 
, then the membership of x to A is undetermined.
From the point of view of the corresponding logic, this would lead to a logic with three truth values: T, F, i (see section 10.1).
The method proposed above can be viewed as a generalization of this simple idea.
It is natural to try to apply inference rules from classical logic to non-classical logics. For example, the resolution method was extended (by C. Chang) more than 30 years ago from FOL to first-order FL. But first we must formally define the semantics of FL.
10.2.1.1. Syntax
The same as for classical logic.
10.2.1.2. Semantics
The only difference with FOL (that corresponds to intuition) is that every predicate P(n) is not interpreted as an n-ary relation (i.e. the set of n-tuples of the relation) in the universe of discourse, but as a fuzzy set, or more precisely the corresponding generalized characteristic set (in other words, to every n-tuple (x1,…, xn), we do not assign true or false to P(n) (x1, …, xn), but a value in [0, 1], which is given by the characteristic function).
It is thus possible to view classical logic as a particular case of FL.
The semantics (i.e. the value given to) composed wffs is given by the function v defined below.
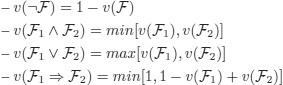
or:
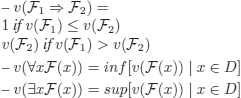
An interpretation 
satisfies (respectively, falsifies) a formula 
iff (respectively < 0.5).
EXAMPLE 10.10.– Consider the wff ∀x∃yP(x, y)
on domain D = {a1, a2}
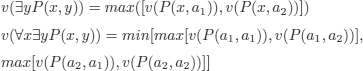
The next step is to find a universe on which it is sufficient to focus to test whether a wff is contradictory.
10.2.2. Herbrand’s method in FL
The key property (see theorem 5.7) is that given a set of clauses S, we can associate to any interpretation of S a Herbrand interpretation 
such that if 
then 
.
We show this on an example.
EXAMPLE 10.11.– Consider the clause:
and the interpretation :
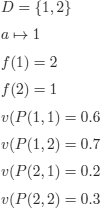
This interpretation is a model of 
. Indeed, 
The corresponding interpretation H is:
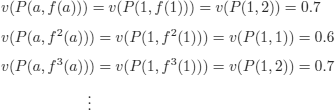
Semantic trees are defined in the same way as for FOL, by replacing L with 
and 
by (L) < 0.5.
10.2.2.1. Resolution and FL
In PL, the resolvent is a logical consequence of the parent clauses (i.e. every model of the parent clauses is a model of the resolvent).
We first analyze an example the way the resolution rule for PL transmits truth values when it is applied to FL.
EXAMPLE 10.12.– Consider the two following clauses:
(whose resolvent is Q)
with:
hence, there is a difference with classical PL:
This example is a particular case of the following theorem.
THEOREM 10.1.– Let C1 and C2 denote two clauses and (C1, C2) denote a resolvent.
If max[(C1), (C2)] = b and min[(C1), (C2)] = a > 0.5
then:
PROOF.– C1: P ∨ , C2: ¬P ∨ ( and : disjunctions of literals)
(C1, C2): ∨
Without loss of generality, we assume:
* a ≤ b and:
from (1) and (2) and by definition of max:
there are two cases to consider:
i) () =
ii) () < a, from (1) (P) = a
By hypothesis a > 0.5, hence (¬P) = 1 − (P) < 0.5 < a from (2) and *() = = b ≥ a
This theorem can easily be generalized.
THEOREM 10.2.– Consider the set of clauses S = {C1,..., Ck} (k ≥ 2)
If 
then
.
10.3. Modal logics
In a dictionary on language sciences (O. Ducrot and T. Todorov), it is written:
Logicians and linguists have often deemed it necessary to distinguish, in an enunciation act, a representative content, sometimes called dictum (relating a predicate to a subject), and an attitude expressed by the subject speaking of the content, that is the modus or modality.
The four following sentences have the same dictum, but different modalities:
– Peter will come.
– Let Peter come!
– It is possible that Peter will come.
– Peter must come.
Modal logic studies modalities, i.e. the logical operations that qualify the assertions (or more precisely that qualify their truth modes). We will say, for example, that a proposition is necessarily true, or possibly true, or that it has always been true, or that it will be true one day, or that we know that it is true, or that it should be true, etc.
Originally, modal logic was designed to characterize the possible and necessary truths. It was progressively extended to the study of statements on knowledge, beliefs, time, ethics, properties of programs, etc.
They are particularly relevant in AI, for example, in the so-called description logics for ontologies and in multi-agent systems.
The concepts of necessity and of possibility have been studied by philosophers, ever since Aristotle, at least.
It is generally acknowledged that C.I. Lewis (in the 1930s) first studied these modalities. His analysis was mainly concerned with strict implication, thus called to be distinguished from material implication and its paradoxes (see exercise 3.7).
A strictly implies B (written A → B) iff A∧ ¬B is impossible, or, with modern notations,
¬
(A 
¬B) or, equivalently, (A B)
where is interpreted as possible and is interpreted as necessary.
Little by little, the study of the connectives and themselves became a field by itself.
For example, in computer science, when referring to a non-deterministic program, means “in every execution that halts, A is T”, whereas A means “there exists an execution that halts with A T”.
Gödel was interested in modalities from the point of view of provability.
For historical purposes, i.e. Aristotle’s philosophy and its huge influence on Western culture, those that were the most studied are:
– ontic modalities: it is necessary (possible, impossible,…) that…
– epistemic modalities: Peter knows that…
– temporal modalities: since, starting from, until, he always thinks that…
– deontic modalities: it is forbidden, it is permitted, it is illegal…
Other modalities:
– doxastic modalities: we believe that,…
– metalogic modalities: it is provable that, this is satisfiable,…
There exist propositional, first-order and higher-order modal logics. We restrict ourselves to propositional modal logics (we will see they have a great expressive power).
One essential characteristic of these logics is the fact that their connectives are not truth functional.
EXAMPLE 10.13.– (See example 2.6.)
Consider the conjecture (we could have chosen any other one)
P = NP
It could be T or (exclusive or) F, but the propositions:
(P = NP): It is possible that P = NP
(¬ (P = NP)): It is possible that P ≠ NP
could both be considered as true propositions. We thus have (no matter the value given to P = NP):
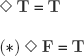
On the other hand:
1 + 1 = 3 is F and it is normal to consider (1+1 = 3) as F. In other words, we do not imagine that it is possible for 1 + 1 = 3 to be T.
By replacing F in (*) by 1 + 1 = 3 (i.e. by F), we obtain:
By considering propositions (*) and (*) (*), we verify that (connective meaning possibly) is not truth functional.
10.3.1. Toward a semantics
There exist relational (possible worlds), algebraic, and topological semantics.
We will study the semantics that is best known: the semantics of possible worlds.
The notion of possible worlds seems to have been around at least since Leibniz. Wittgenstein used to talk of the possible state of things.
In a book that is considered as a reference in logic (and that ignores modal logic)6, it is written:
“…Therefore, a ‘possible world’, or model of [a language] …”
This seems to show that the transition from one to the other (i.e. from classical logic to non-classical ones) can be made naturally via the notion of possible worlds.
To better see the relationship between the notion of a model in classical logic and that of a possible world, we consider the formula: [(A ∨ B) C] ⇔ [(A C) ∨ (B C)]
and the interpretations:
We can imagine that each Ii(1 ≤ i ≤ 4) corresponds to a situation, a moment, a state, a state of knowledge, a world, etc.
These interpretations can be represented as worlds (we only provide the elementary propositions that are evaluated to true).
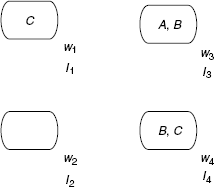
We can also add a relation between these worlds (which leads to the so-called Kripke semantics or the possible worlds semantics).
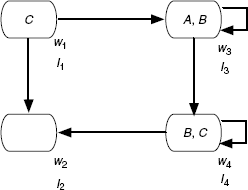
And instead of saying:
(CL) Formula 
is satisfied (or not satisfied) by interpretation I
we will say:
It will also be possible to construct formulas mentioning different worlds.
REMARK 10.7.– The notion of possible worlds is familiar (not necessarily with the same name) in the study of probability theory. For example, when analyzing the logical possibilities of the results of an arbitrary experiment (for example, throwing a die).
More formally.
10.3.1.1. Syntax (language of modal logic)
< formula >::=< atomic formula >| ¬ < formula >|< formula > ∧ < formula >|< formula > ∨ < formula >|< formula >< formula >|< formula >⇔< formula >| <formula > | < formula >
< atomic formula >::= Pi (i ≥ 0) 7
or more concisely:
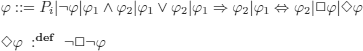
One of the characteristics of modal logics is their “parametrized flexibility”. This sentence, whose meaning will be made accurate in what follows, is metaphorical and expresses the fact that the new connectives that are introduced by these logics can be used to express very different characteristics in very different domains. For example, consider the different meanings of formula :
: necessarily
: in the future always
: it must be the case that
: we know that
: we believe that
: after any execution of the program has halted, we have
: in Peano’s arithmetic we can prove
10.3.1.2. Semantics
DEFINITION 10.8.– (Kripke semantics, Kripke models).
– A modal frame or K-modal frame is a pair = (W, R)
where W is a non-empty set and R is a binary relation on W.
– A Kripke model8 is a triple:
with:
– W: non-empty set (of worlds);
– R: binary relation on W (accessibility relation);
– : 
or : 
(
: set of all atomic propositions (formulas). 
and 
, respectively, denote the sets of parts of and 
);
– is called the interpretation function or valuation
( indistinctly provides the set of worlds in which a proposition is evaluated to T or the set ofpropositions that are evaluated to T in each world)
– we shall indistinctly say w ∈ W or w ∈
;
– the frame is called the base of the model.
– The domain of is extended to the set of formulas ( is an arbitrary formula) 
.
DIGRESSION 10.1.– Kripke defined propositions as functions from the set of worlds to the truth values and an n-ary predicate as a function from the set of worlds to the set of n-ary relations.
DEFINITION 10.9.– (satisfiability, validity). In what follows, is a wff and Mod is a set of Kripke models 
.
means: the formula is satisfied in the world w of the model . The relation |= is defined as follows (Mod denotes a set of models):
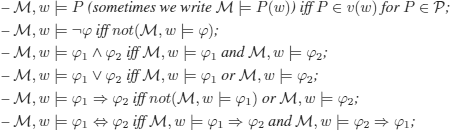
iff for all w' such that R(w, w'): 
: necessarily , or is necessarily T 9;
iff there exists w' such that R(w, w'): 
: is possible or p is T in a possible (accessible) world;
– is Mod — satisfiable iff there exists 
Mod and 
such that 
, w 
;
– is valid in model 
(
∈ Mod), written 
iff v() = W (i.e. iff for all w ∈ W 
– Mod — valid iff is valid in all models in Mod;
– is valid in modal frame (W, R) iff is valid in all models admitting (W, R) as a base;
– A model is finite iff the set of worlds of the modal frame is finite; it is infinite otherwise10.
REMARK 10.8.– The underlying notion of necessity in the definition is not always related to a necessity in the real world, as we see it. There could be, for example, several parallel worlds (or flows of time) that coexist (that flow at different speeds) and we only have access to one of them.
We obtain different logics by imposing conditions (in particular none) on the accessibility relation. The best-known logics are K, S5, S4 etc.
These logics can also be characterized by formal systems.
EXAMPLE 10.14.– Consider the Kripke model represented by the graph below. We indicate the corresponding interpretation in each world. The edges of the graph define the accessibility relation.
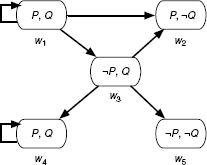
In this model , we have:
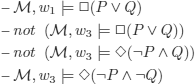
10.3.2. How to reason with modal logics?
Similar to classical logic, there are different approaches. We shall study the following ones:
– syntactic approach (formal systems);
– direct approach;
– translation approach.
In the first approach, we provide a formal system (see section 3.3) for the logic under consideration. In the direct approach, we give inference rules for the modal connectives, and in the translation approach, we translate formulas into FOL and reason in FOL11.
We present here the syntactic approach and the translation approach for some propositional modal logics. The direct approach is treated for temporal logics, which can be considered as particular cases of modal logics.
10.3.2.1. Formal systems approach
We specify those that are best known. The language is still the one of section 10.3.1.1.
– The minimal logic K (K as Kripke)
(axioms):
All tautologies of PL12 
(P Q) (P Q).
(inference rules):
MP: 
necessitation :
substitution % see remark 3.20
Other logics
– Inference rules: the same
– Axioms:
– T = K {P P}
– D = K {P P}
– S4 = K {P P,P P}
– S5 = S4 {P P}
– G = K {(P P) P}
EXERCISE 10.5.– Give the proofs (deductions) that correspond to the following theorems:
a) 
b) 
c) 
d) 
e) 
f) 
g) 
h) 
10.3.2.2. Translation approach
The connectives that are difficult to translate are and . The translation function (Andréka, Németi, and Van Benthem) tr (see definition 10.9) is defined as follows:
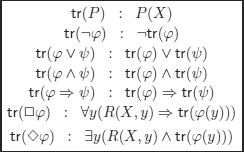
P: propositional symbol.
X: free variable, denoting the world in which we are.
y: fresh variable not occurring in the formulas to be translated.
R: accessibility relation.
The idea behind this translation is of course the capture of the semantics imposed by the definition: P(y) (respectively, (y) should be interpreted as P (respectively, ) is T in world y.
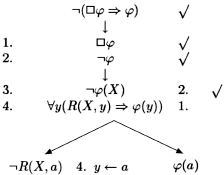
EXAMPLE 10.15.– The formula whose validity is to be proven is:
This is the “specifically modal” axiom of logic K (see definition 10.10). Note that no particular property is imposed on the accessibility relation (this should be compared with exercise 10.7).
EXAMPLE 10.16.– Using the translation method and the method of semantic tableaux:
a) give a Kripke model such that in a world w1: ,w1 |= (P Q) and , w1 
(P Q);
b) give a Kripke model such that in a world w1: ,w1 P Q and ,w1 (P Q).
a) We consider the set {(P Q), ¬(P Q)}
Translation:
REMARK 10.9.– The constants that are introduced by variable instantiations (here a) correspond to accessible worlds.
The branch going through leaf 12 cannot be closed by instantiating the only formulas that can still be instantiated.
We have constructed the desired model:
b) We consider the set {P Q, ¬(P Q)}
Translation:
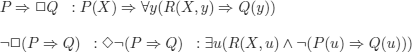
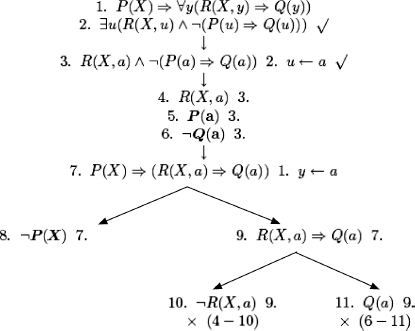
We have constructed the desired model:
EXERCISE 10.6.– (sea battle argument). Express the following argument (given by Aristotle) in modal logic and verify its correctness using the translation approach.
(Similar to classical logic, given an argument expressed in a natural language, the classification of this argument as correct or incorrect will generally depend on the way it is translated.)
If I give the order to attack then necessarily there will be a sea battle tomorrow. Otherwise, necessarily, there will be none. I either give the order or I do not give it. Hence, necessarily, there will be a sea battle tomorrow, or necessarily there will be none.
Two classical translations of the sea battle argument are given below:
P: “I give the order to attack”;
Q: “There will be a sea battle tomorrow”.
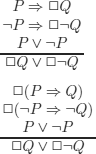
EXAMPLE 10.17.– (accessibility relation for T, S4, S5). We can use the translation method and the method of semantic tableaux to try to discover the sufficient properties that are required of the accessibility relation so that the following axioms are valid.
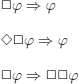
If R is reflexive, i.e. ∀xR(x, x), then we can graft to each branch of the tree:
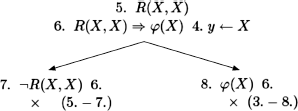
and the two branches can be closed.
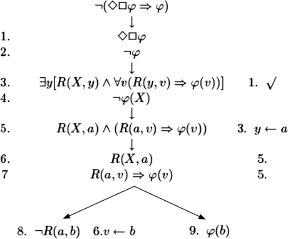
If R is symmetric, i.e. ∀x∀yR(x, y) R(y, x), then we can graft to each branch of the tree:
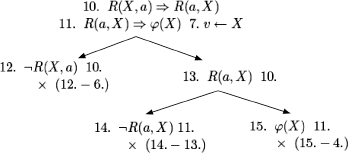
and the two branches can be closed.
If R is transitive, then the branch on the left-hand side can also be closed, by grafting to node 11 the tree below:
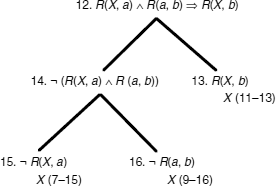
As an example, we give here a proof of this property that is representative of the properties that appear in textbooks on this topic.
is valid in a modal frame iff the accessibility relation R is transitive.
if
We show that if R is transitive and we have
then we also have:
R is transitive, i.e.:
hence, if formula is satisfied in world w1, then it is satisfied (see definitions 10.8 and 10.9) in all worlds that are accessible from (related to) w1; hence, it is satisfied in w3, so that () is also satisfied in w1.
only if
We prove the contrapositive, we assume that R is not transitive and we need to prove that:
and that:
to do so, we propose, for example, (w2) = ; (w3) = ¬.
This valuation is possible as R is not transitive; hence, we may assume that we have ¬ in w3. This would not be possible if R had been transitive, as we assumed:
and if R had been transitive, w3 would have been accessible from w1, and by definition of the semantics, is T in a world iff is T in all worlds accessible from the world we are starting from (see definition 10.9).
With our approach, we could also have proved the only if part of the theorem (the if part has already been proved):
If R is not transitive, we graft to node 11. the tree:
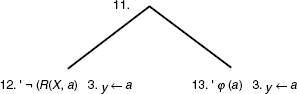
By considering the branch going through nodes 7, 9, 10, 11, 13, and by applying the same method as in example 10.16, we obtain the Kripke model (interpretation):
which verifies:
and:
EXERCISE 10.7.– Use the translation method and the method of semantic tableaux to discover (sufficient) properties of the accessibility relations of the modal frames in which the following formulas are valid:
a) 
b) 
c) 
d) 
e) 
(called Geach’s axioms)
A question that naturally arises is whether other axioms (formulas) correspond to other simple relations, or if we can always express these relations by FOL formulas.
REMARK 10.10.– The problem of knowing whether an arbitrary wff of modal logic is satisfied by Kripke frames that are characterized by FOL formulas is undecidable. But Sahlqvist’s theorem guarantees that a (syntactically characterized) class of formulas of modal logic corresponds to Kripke frames that are definable by FOL formulas. Sahlqvist’s class is decidable.
The two following formulas do not belong to Sahlqvist’s Class.
McKinsey’s axiom:
(MK)
(S4.1 = K {MK})
and Löb’s axiom:
cannot be defined by a set of wffs of FOL.
Furthermore, there exist formulas of modal logic that are valid in frames that are characterizable by FOL formulas, but are not equivalent to formulas in Sahlqvist’s class, for example:
As a consequence, we can consider the expressive power of the PLs.
Propositional modal logic corresponds to a fragment of SOL.
As can be seen, for example, in exercise 10.6, Aristotle was interested in other arguments than those of his syllogistic (see section 2.2). A well-known argument that he proposed on the need to philosophize is part of deontic logic:
We must philosophise or we must not philosophise. If we must philosophise then we must do so. Otherwise, we must still philosophise (to justify this point of view). Therefore, in all cases, we must philosophise.
EXERCISE 10.8.– How would you define the semantics of the following operators from deontic logic, using the semantics of possible worlds?
O: is compulsory
F: is forbidden
P: is allowed
E: is optional
10.4. Some elements of temporal logic
When I am not asked, I know what time is; when I am asked, I no longer do.
Saint Augustin
The notion of time is essential in philosophy, in physics, in biology, and also in computer science (sequential and parallel algorithms, time complexity of algorithms, etc.).
In philosophy, it leads to different positions, it suffices to consider Parmenides for whom “nothing changes” and Heraclitus for whom “everything changes”. See also exercise 10.6. This notion is closely related to notions of space, matter, energy, evolution, etc. Its conceptualization poses huge problems and it is difficult to try avoiding them, as time is implicitly or explicitly present in all human activities (and all around us).
We often use metaphors to mention time (the flow of time, time’s arrow, etc.).
Similar to other topics, a logical study of time only aims at capturing some aspects that are relevant for the class of problems that are studied.
The notion of organization of instants:
seems to be the most fundamental one.
In mathematics (in the statement of definitions, theorems, etc.), we are not interested in time. This is not the case in natural languages. Linguists have studied the way time can be taken into account in logical structures.
For example (as is also common in physics): vt0,vt1,vt2, …(i.e. the speed of an object at times t0, t1, t2,…) or by explicitly introducing time as a parameter: interests(x, 
), alive(x, t), etc.
We can also (and this possibility is of a particular interest to us) treat instants as possible worlds (now corresponds to the world we are currently in). The accessibility relation will be a total order (linear time) or a partial one (branching time13).
Reference to the past and to the future depends on languages and is not always that obvious. For example, in English, we say:
– the plane is scheduled to land at 6:30 pm (and it is currently 3:10 pm, we use the present tense to talk of the future);
–I now understand the rules of rugby (we are using the present tense to talk of an event that belongs in a large part to the past: the understanding of the rules).
Problems about the nature of time and temporal concepts have been a concern for philosophers at least since there has been a written philosophy.
Time is part of our sensory experience (at least indirectly), and our discourse relies heavily on time (in the sentences above, for example).
Classical mathematical logic abstracts time away. The propositions that are obtained from sentences from everyday life are sometimes very artificial.
The goal of temporal logic (also called tense or change logic) is to systematize reasoning with propositions involving temporal aspects.
The Megarian and Stoic Greeks studied theories for these logics.
Modern temporal logic was initiated by the work of logician and philosopher Arthur N. Prior in the 1950s. Prior systematically studied the links between temporal and modal logics.
The representation (picture) of time as dots that denote instants without duration as basic entities is frequently used. Examples are graphs representing functions of time (speed, distance travelled, GDP, unemployment rate, etc.) that are used to teach physics, economy, etc. where in each instant (point) on the abscissa is assigned an ordinate point.
We must distinguish between the graphs of functions that correspond to continuous phenomena and those that correspond to discrete phenomena.
Although common, the concept of time as a set of instants without duration is a very abstract model, compared to our perception in everyday life, and it is similar to the notion of a point in space (what exactly is a region of space, say, a sphere of radius 0?).
Another basic entity that is widely used is the period or interval.
Depending on the problem under consideration, one or the other notion will be better adapted.
In particular, there are problems that cannot be solved with one of these notions, but can be with the other (or not even be problems at all for the other). Here is an example dating at least from the Middle Ages: at the precise moment a man dies, is he alive or dead?, or at the precise moment afire is put out, is it burning or extinct?
This problem cannot be solved with the notion of instants, but with the notion of time interval, there is no problem at all: the man died between 2 and 3 am, if he was alive at 2 am and dead at 3 am.
If we use a discrete model for time, then there is no problem either.
Under some circumstances, it is more interesting to consider both notions at the same time. For example, if we say Alice and Bob took the 6:42 train and chatted throughout the entire trip, we are likely to be considering the departure time as an instant and the duration of the trip as an interval.
When the basic entities are instants, the relations before and after are used.
For periods or intervals, the following relations (among others) are used: overlap, non-overlap, meet, start and finish
We provide a graphical representation and logical translation of each relation, using as primitive relations the precedence relation (
) and the interval inclusion relation (
). Given two intervals A and B, they can be related the following ways (among others):
.Overlap:
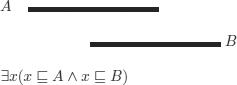
(Note that x denotes an interval.)
.Non-overlap::
.Meet:
.Start
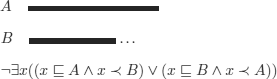
.Finish
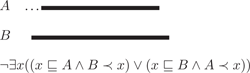
10.4.1. Temporal operators and semantics
As was mentioned in section 10.4, Prior introduced modern temporal logic essentially for philosophical purposes and he naturally focussed on linguistic constructions.
Natural languages and the inferences that are performed on their sentences provide examples of the peculiarities that come up when time is taken into account.
For example, from The weather is nice and The weather is cold, we can (correctly) deduce that The weather is nice and cold. From The weather will be nice or The weather will be cold we can deduce The weather will be nice or cold. But starting with The weather will be nice and The weather will be cold, we cannot (correctly) deduce that The weather will be nice and cold.
We introduce the following operators:
F: at some point in time, it will be the case that (it will be the case at least once);
P: it was the case at some point in time that (it was the case at least once);
G :def ¬F¬: it will always be the case that p;
H :def ¬P¬: was always the case in the past.
For the Megarians (philosophers of the school of philosophy founded by Euclid of Megara)14:
– the real is what is realized (i.e. true) now;
– the possible is what is realized (i.e. true) at some arbitrary time;
– the necessary is what is true all the time.
With modern notations, we have the following respective translations for “possible” and “necessary”:
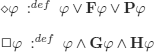
For Stoicians:
– the real is what is realized (i.e. true) now;
– the possible is what is realized (i.e. true) now or at a future time;
in other words:
a proposition is possible if it is true or will be true;
– the necessary is what is realized (i.e. true) or will be realized at all future times.
With modern notations, we have the following respective translations for “possible” and “necessary”:
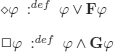
Note that with one or the other definition, “possible” and “necessary” keep their usual relationship.
10.4.1.1. A famous argument
Some Greek philosophers credit the Greek philosopher of the Megarian school Diodorus Cronus (– 4th) with a famous argument (that was analyzed by Prior) called the Master argument, that seems to be the following:
D1) Every true proposition about the past is necessary;
D2) An impossible proposition cannot be a consequence of a possible proposition;
D3) There exists a proposition that is possible, but is not and will not be true.
Diodorus concludes (the reasoning to reach the conclusion is unknown) that the set {D1, D2, D3} is unsatisfiable, which allowed him to characterize:
– the possible as what is or will be true;
– the impossible as what, being already false, will not be true;
– the necessary as what, being true, will not be false;
(Some authors translate: the necessary as what is and will be always the case (true).);
– the unnecessary as what is already false, or will be false.
Logicians and modern philosophers tried to reconstruct and formalize Diodorus’s reasoning to conclude that {D1, D2, D3} is unsatisfiable.
One of the formalizations translates Diodorus’s assertions as follows:
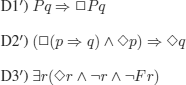
and adds the following two assertions that were (according to historians) accepted by the Greeks.
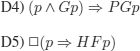
The proof of the unsatisfiability of {D1', D2', D3', D4, D5}:
The logic that corresponds to Diodorean logic is:
meaning that we add Geach’s axiom to S4 (see exercise 10.7), which is valid in directed frames (directed relations correspond to the so-called (strongly) confluent in λ-calculus):
For temporal frames (T, ≤), it is often expressed as:
10.4.2. A temporal logic
Given the language of PL enriched with operators F, P, G, H and formally defined by the following syntactic rules:
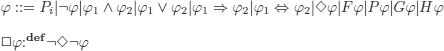
a model for this language is a triple 
where:
T is a set of instants.
We restrict ourselves as follows:
is a total order relation (see definition 3.25) % Other hypotheses (density, etc.) lead to other temporal logics
(valuation) →2T
(where is the set of basic symbols and 2T is the set of subsets of T)
We will say that is true at instant t in model , which will be denoted by 
and by 
, where relation is defined inductively as follows:
iff t ∈ v(P) % P : propositional symbol
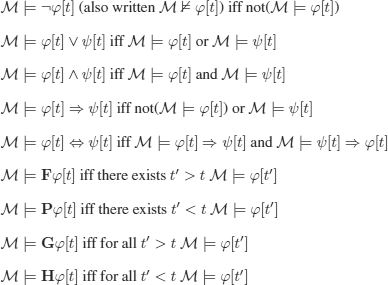
A wff [t] is T iff (T,<,v) = [t] for every valuation v; is T, noted = , iff [t] is T for all t ∈ T.
10.4.3. How to reason with temporal logics?
Similar to modal logics, we can envisage formal systems or translation methods. For the temporal logic defined in section 10.4.2, we will propose a direct method: the method of semantic tableaux. We apply the same process as for classical and many-valued logics. We shall start by the rules that define the semantics to define the syntactic rules (that respect this semantics) that will allow us to construct the tableau.
As in its previous versions, the method of semantic tableaux enumerates the sets of (partial) models of a set of temporal formulas, in which time occurs. The considerations of section 3.2 about the usage of the method apply.
The following remarks are important:
– there is a new parameter: time. As mentioned, we restrict ourselves to totally ordered instants:..., t-n,t-(n-1),..., t-1,t0, t1,t2, …,tn,…;
– the contradictions that permit us to close a branch (and thus to conclude that it is impossible to construct the potential model that is represented by the branch) between a formula p and its negation ¬ must correspond to the same instant (which is rather obvious: there is no contradiction in the fact of being alive at instant ti and not alive at instant tj, where i ≠ j!);
– when applied to a formula at instant ti, the rules that are concerned with connectives ¬, ∧, ∨, , xand ⇔ will permit us to replace by the formulas denoting all models of at the same instant ti. As usual, we shall tick as already analyzed (√);
– rules F, P, ¬G, and ¬H below apply only once and will therefore be ticked after being used (√). Rules ¬F, ¬P, G, and H below can be applied at any desired instant. We will not be interested in the problem of decidable subclasses.
The rules are therefore the following:
10.4.3.1. The method of semantic tableaux
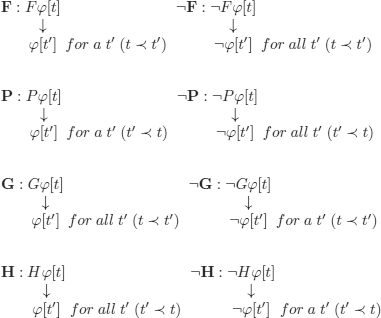
EXAMPLE 10.18.– Prove the validity (or non-validity) of the formula below, using the method of semantic tableaux:
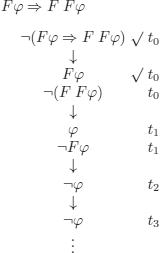
Of course, every ti is different from the other tj’s (i ≠ j).
The considered formula is not valid. Counter example (i.e. model of its negation):
{|[t1] ¬[t2]}.
EXERCISE 10.9.– Use the method of semantic tableaux to prove the validity (or nonvalidity) of the formulas below:
EXERCISE 10.10.– Prove the validity of formula:
using the method of semantic tableaux.
The two following operators are particularly important in computer science and confer a great expressive power to temporal logic. These are: since and until:
: it was the case that and since then and up till now (t0) it was the case that ψ.
: it will be the case that and from now (t0) until then it will be the case that ψ.
Their translation in FOL is:
In computer science, temporal logics are used in program verification, AI, databases, etc. They are used for the analysis and proofs of properties verified by many systems, including those that are concurrent, non-deterministic, real time, that do not end, etc.
The following relations are often studied in temporal logic:
irreflexivity: 
asymmetry: 
transitivity: 
there exists a beginning: 
there exists an end: 
linearity: 
discrete: 
(To be compared with the notion of density below.)
density: 
Warning: density ≠ continuity
DIGRESSION 10.2.– (on continuity). A total ordering (S, R) is continuous if it does not contain any gap.
A cut is a partition (X, Y) (i.e. S ⊆ X Y and X 
Y = 
) such that:
A gap is a cut (X, Y) such that X has no last element and Y has no first element.
((
, ≤) has gaps: take the cut 
REMARK 10.11.– The formula ∨(Gp PGp) (Gp Hp) is valid in all continuous frames.
10.4.4. An example of a PL for linear and discrete time: PTL (or PLTL)
10.4.4.1. Syntax
o : next
: eventually
: always
U : until
10.4.4.2. Semantics
= (T,S, )
T: a finite or denumerable set of states (instants)
S: total function (successor function): T → T
s0: first element
(as usual, we shall note Si(t):
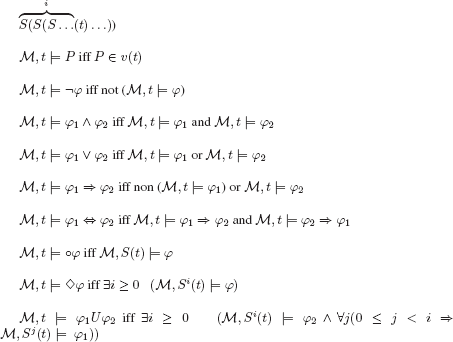
An interpretation (model) satisfies a formula iff 
10.4.4.3. Method of semantic tableaux for PLTL (direct method)
It is based on the same principle as the method used for PL and FOL, i.e. we enumerate all the models of a set of formulas. To do so, we propose the following rules that translate the semantics of the connectives that appear in the syntax (section 10.4.4.1). The rules that correspond to the classical connectives are the same as those for PL.
Rules:
→: decomposition of the wffs (independent of time). % see below;
: corresponds to moving forward one unit of time. % see below.
Once the principle mentioned above has been accepted, two new problems related to time arise:
1) the rules on and U;
2) how to close a branch.
1) These rules can generate a potentially infinite tree, if we systematically choose the rightmost branches (they replace a formula by another formula containing the same connective).
To solve this problem, each time a formula is replaced, it is marked as already developed but still kept (we memorize that it has been developed). If at a given time (see below (*)), say tk, we obtain the same set of formulas as one occurring at a previous instant, say ti, we add an edge: tk → ti. This will lead to a directed graph instead of an infinite tree (see digression 3.1).
2) If at a given instant we have two contradictory literals Pi and ¬Pi, then the model we are trying to construct is not viable and we say the branch is unsatisfiable.
If there is a cycle in a branch, this means that an event (f, f U g) will never occur. We will therefore never be able to construct a model on the branch containing the cycle. The node from which the branch originates will be classified as unsatisfiable.
Of course, if all descendants of a node n are unsatisfiable, then n will be classified as unsatisfiable.
(*) …But we still have not mentioned time!
Here is how we proceed: we first decompose (i.e. we apply the rules on) the formulas that do not begin with o. When they have all been decomposed, we decompose those beginning with o (we move forward one unit of time).
EXERCISE 10.11.– Use the direct method for PLTL to prove the unsatisfiability of the following formula:
You will need to propose a rule for P (use the definition from section 10.4.4.1).
1) is satisfied by every interpretation such that every state in which P is true is followed by a state in which Q is true.
2) is satisfied by every interpretation such that if P is true in a state then starting from the next state, Q is always false until the first state in which R is true.
3) is satisfied by every interpretation in which P is true infinitely many times.
EXERCISE 10.12.– Can you justify the assertions (1), (2), and (3) of example 10.19, using the translation method and the direct method of semantic tableaux?
1 The intension is the set of characters that are (considered as) essential to a class.
2 What possesses an existence of its own, independently of the knowledge or the idea that cognitive beings can have about it.
3 For example, in practice, saying that two objects have the same color means that the potential differences are not detectable by the sense (or device) that detects colors.
4 The solution is given by J. Goguen.
5 The required properties on generalized characteristic functions are a key point in the formalization of FLs.
6 Chang and Keisler: Model Theory.
7 It is worth mentioning that Aristotle was the first to use propositional variables, i.e. letters that can be replaced by propositional symbols and not by terms (of a syllogism, see definition 2.8) in modal logic.
8 Note that, in accordance with usage, we talk about Kripke models and not Kripke interpretations. Thus, a formula may be evaluated to F in a Kripke model. We may also talk of the Kanger-Kripke semantics.
9 A necessary truth is a truth that is verified in all possible (and accessible) worlds.
10 As in the case of FOL, the property of admitting finite models (see definition 5.15) is important for the design of decision procedures for modal logics.
11 Previously, the founder of temporal logic, appears to be a pioneer of the translation method.
12 Note that we could have chosen any complete formal system, for example, Si (see section 3.4) for PL. The choice that was made permits us not to have to (re)prove all theorems (tautologies) of PL.
13 In branching time, we can have t1 Rt2 ∧ t1 Rt3 ∧ t2 ≠ t3 ∧ — (t2Rt3 ∨ t3Rt2).
14 The author of the famous Elements was Euclid of Alexandria.