Chapter 8

Inference

Inference is one of the most important intelligent activities of a human being. We will study different forms of inference and several aspects of its formalization. According to the dictionary:

Inference: every operation leading to the acceptance of a proposition whose truth is not directly known, thanks to its relationship to other propositions known to be true. This relationship can be such that the inferred proposition is judged to be necessary, or only plausible.

Inference is therefore the most general term of which reasoning, deduction, induction, etc. are instances.

Etymologically: to offer → to infer: to carry into – to put forward

Inference is an underlying activity of almost all our other activities. Something as common as vision, for example, uses it (probably without the knowledge of doing so). When we see someone we know, but who has let his beard grow, is wearing glasses (and did not use to before), has put on some weight or lost some weight, etc. we still recognize him, although from the point of view of appearance, this is someone we have never seen.

There are many different forms of inference, among which are inductive (i.e. general conclusion from particular facts), by analogy, from testimonials, from memories, probable inference, statistical inference, non-monotonic, etc.

We begin with the study of one of the most common forms of inference (often carried out unconsciously), which is often mentioned in this book.

8.1. Deductive inference

As usual, a first approach can rely on the definition in the dictionary.

Deduction: operation by which, starting from one or several propositions taken as premises, we rigorously conclude a proposition that is a necessary consequence, in accordance with logicalules.

Etymologically: to conduct → to lower → to deduce

We shall give several classical types of deductions, focusing on the key problems that arise in the process of their automation, through examples that shed light on these problems.

The typical example of a deduction is the syllogism, which we have mentioned in section 2.2.

The following example is a less known deduction type that leads to interesting problems.

The sorites

Argument consisting of a mass of premises. Polysyllogism, where each conclusion is used as a premise of the following syllogism. In more modern terms, we would say that this is a reasoning with a linear strategy (see example 5.28).

EXAMPLE 8.1.– A is B, B is C, C is D, D is E; therefore A is E.

The name sorites is especially used in the following very old reasoning (see also section 10.2) given by due to Eubulides (see digression 2.2).

Does a heap of grains remain a heap when one grain is removed?

Consider a heap of grains: if we remove one grain, it remains a heap, if we remove another grain, it remains a heap…

Conclusion: a unique grain is a heap…but [everyone agrees that] it actually is not!

It is sometimes presented as follows:

A grain is not a heap, neither are two grains, … After how many grains do we get a heap?

An aspect that is often neglected is that of partial conclusions. It should be clear that a given strategy, when applied to a problem, can lead to the same conclusion going through different partial conclusions, depending on the order in which the premises are considered. The following example given by L. Carroll illustrates this.

EXAMPLE 8.2.– (partial conclusions). Deduce the conclusion with a linear strategy (see example 5.28), considering different orders on the premises (partial conclusions are written in bold).

No A is not B.

Every B is C.

Every C is D.

No not E is not A.

Every H is not E.

Therefore:

Every H is D.

We translate into PL (sometimes the categorical propositions of syllogisms are formalized in this logic) and into clausal form. For deductions, we use the resolution rule with a linear strategy and two different orders.

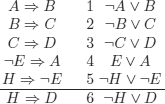
Note that the conclusion (6) is not negated, we do not try to derive but (6)¹.

With the order 1,2,3,4,5:

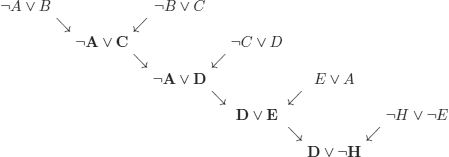
With the order 4,1,5,2,3:

Sometimes, as L. Carroll wondered, it is interesting to obtain all the logical consequences of the premises. The following example shows that this can be really useful².

EXAMPLE 8.3.- (beware of hidden consequences!). From the following premises:

1) Every individual suitable to be a member of Parliament who does not spend all his time making speeches is a benefactor of the people.

2) People with a clear mind and who express themselves well have received a decent education.

3) A woman worthy of appraisal is a woman who knows how to keep a secret.

4) Those who do favors for the people but do not use their influence for praiseworthy purposes are not suitable to be members of Parliament.

5) Those who are worth their weight of gold and are not worthy of appraisal are always unpretentious.

6) Benefactors of the people who use their influence for praiseworthy purposes are worthy of appraisal.

7) Those who are unpopular and are not worth their weight in gold do not know how to keep a secret.

8) Those who know how to talk for hours and hours and are not suitable to be members of Parliament are worthy of appraisal.

9) Every individual who knows how to keep a secret and is unpretentious is a benefactor of the people whose memory will last forever.

10) A woman who does favors for the people is always popular.

11) Those who are worth their weight of gold, who do not stop making speeches and whose memory lasts forever are precisely those whose photography can be seen in all shop windows.

12) A woman who does not have a clear mind and has not received a proper education is unsuitable to become a member of Parliament.

13) Every individual who knows how to keep a secret and does not know how to always make speeches can be sure to be unpopular.

14) An individual with a clear mind, who has influence and uses it for praiseworthy purposes is a benefactor of the people.

15) A benefactor of the people who is unpretentious is not the kind of person whose photography is shown in all shop windows.

16) Those who know how to keep a secret and use their influence for praiseworthy purposes are worth their weight in gold.

17) Someone who does not know how to express himself and is incapable of influencing others cannot be a woman.

18) Those who are popular and worthy of appraisal are either benefactors of the people or unpretentious.

We can deduce, among other things:

A woman is not suitable to be a member of Parliament!

REMARK 8.1.– In PL, starting with a finite set of premises, we always obtain by resolution a finite set of conclusions. This is not the case in FOL: it suffices to consider the set of conclusions of the premises in the following example.

EXAMPLE 8.4.– (complexity of proofs). Consider the following reasoning:

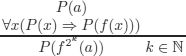
We analyze the complexity of two proofs by resolutions that are obtained with different strategies for k = 3:

1) P(a)

2)

3)

4)

5)

6)

The number of steps in the proof (independently of the choice between forward and backward chaining) is:

A less costly proof:

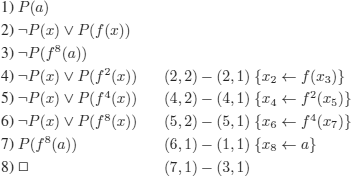
The number of steps in the proof is:

…the difference is essential

EXAMPLE 8.5.– (appearances are deceptive). Consider the following reasoning:

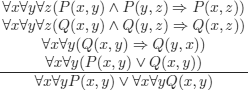
In other words, given a transitive relation P and a symmetric and transitive relation Q, and given that any two elements are related either by P or by Q, prove that P is total or Q is total.

We decide to prove that this reasoning (or theorem) is correct using the resolution rule. We thus translate into clausal form (after negating the conclusion and Skolemization, we obtain clauses 5 and 6).

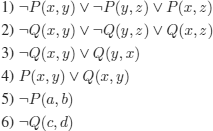
We must find a refutation by resolution of the set of clauses above.

Note that this set of clauses belongs to a decidable fragment of FOL (finite Herbrand universe), so we are sure that the search halts and that the set is either unsatisfiable or satisfiable.

The proposed solution involves a typically human “trick”:

– we know that unit clauses are useful (the resolvent contains less literals than the non-unit parent clause);

– we therefore try to generate unit clauses (we will also use hyperresolution to obtain clauses 10, 11, 12, 16, 12', 14'),

– for any closed term in the Herbrand universe of a set of clauses S and for any predicate P occurring in S, we have either or .

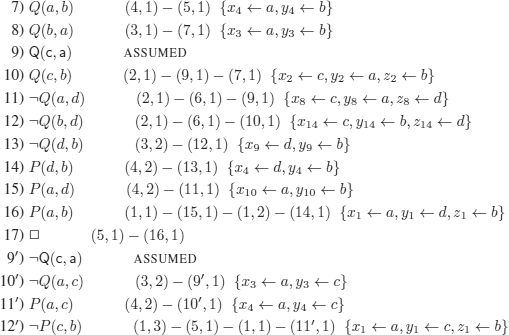
REMARK 8.2.– The trick that was used corresponds to the law of excluded middle in some so-called natural deduction systems:

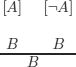
The formulas between [ ] are discharged or cancelled: they are no longer useful (see digression 3.5).

The rule reads: if from A we can deduce B and from A we can deduce B then B.

8.2. An important concept: clause subsumption

In informal reasonings, to derive a conclusion (or verify that a reasoning is correct), we frequently use the fact that a property or relation satisfied by all the objects of a universe is also satisfied by particular objects of this universe (see, e.g. example 5.1). We also use the fact that when we have a disjunction, whatever makes a subset of the disjuncts true also makes the entire disjunction true.

These two very simple remarks are used in definition 8.1. According to the dictionary:

To subsume: fact of considering a thing as being a member of a whole. Considering an individual as being a member of a species, or a species as being a member of a genus; considering a fact as the application of a law.

Classification,³ which deals with the domain of systematics (or taxonomy) and is used especially in botany and zoology, beginning with the work of the great Swedish botanist Carl von Linné (18th Century), structures the objects considered in these sciences with a partial order relation (corresponding to inclusion): race, species, genus, family, order, class, type and reign.

There exist many knowledge representation languages (among which the classical languages are KL-ONE, KRYPTON, LILOG, etc.). Languages such as KL-ONE, which was frequently used in natural language-processing systems, enable us to describe concepts using unary predicates.

Knowledge is separated into:

– a terminological part (concept definition): the T-box;

– an assertional part (database): the A-box.

The language that is used by the T-box corresponds to a fragment of FOL.

Subsumption determines the order relation (with as an order relation) between concepts.

Concept C is subsumed by concept D if all the instances of C are necessarily instances of D, meaning that the extension of C is interpreted as a subset of the extension of D (see digression 8.1).

This very short motivation is meant to show that to dispose of a method (if possible a decision procedure) to decide whether relations hold between certain formulas can be very useful in knowledge manipulation.

DEFINITION 8.1.– (clause subsumption). A clause C (θ)-subsumes or simply subsumes a clause D iff:

i) there exists a substitution such that:

θC is a sub-clause of D (if clauses are considered as disjunctions of literals).

or:

θC D (if clauses are considered as sets of literals).

We will write C ≤_s D.

In general, we impose that:

ii) number-of-literals(C) ≤ number-of-literals(D)

(or card(C) ≤ card(D))

We say that C is more general than D. This terminology is easy to understand if we take into account the fact that C contains more (universally quantified) variables than D (see also exercise 8.1 a)).

REMARK 8.3.– This definition applies to PL with θ = (see rule R-4 of the Davis-Putnam method, section 3.5).

Condition (ii) is sometimes justified by the fact that:

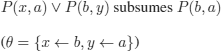
This definition can be considered as somewhat “unnatural”, because we may keep a more complex object in the inference process.

EXAMPLE 8.6.– P(x) ∨ Q(y) subsumes P(a) ∨ Q(b) ∨ R(u, z)

EXERCISE 8.1.–

a) Prove that if C subsumes D, then C D.

b) Is the problem does C subsume D decidable?

8.2.1. An important problem

Can we say: if C D, then C subsumes D?

Consider:

We prove that C D, using the resolution method; we must thus show that C ∪ {¬D} R

(i.e. there are four clauses, see also exercise 5.3 (l))

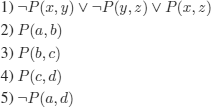
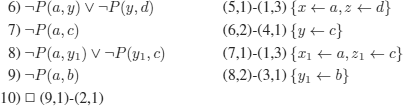
…but C does not (-) subsume D:

indeed, the desired substitution must contain {x ← a,z ← d}, which requires either y ← b; C will then contain ¬P(b, d), and the subsumption is impossible; or y ← c; C will then contain ¬P(a, c), and the subsumption is impossible.

We give another example showing that if C subsumes D, then D is a logical consequence of C, but that the converse does not hold.

We use the resolution method to show that C D

{C, ¬D} is the set of clauses 1, 2, 3 below:

REMARK 8.4.– Given two clauses C and D, the problem C ^? D is undecidable.

This answer, together with the answer to exercise 8.1 (a), also allow us to show that clause subsumption and logical consequences between clauses are not equivalent.

The following theorem, which is admitted without a proof, indirectly gives the key (auto-resolvent clauses) to the non-equivalence between subsumption and logical consequences between clauses.

THEOREM 8.1.– If C is a clause that is not auto-resolvent and D is a non-tautological clause, then C D iff C subsumes D.

DEFINITION 8.2.– Let C be a clause. We denote by:

C⁺ the set of positive literals in C;

C^– the set of negative literals in C.

C is ambivalent iff there exists a predicate symbol in C that occurs in C⁺ and in C^–4.

An immediate consequence of this definition is that a positive (respectively, negative) clause cannot be ambivalent.

THEOREM 8.2.– Let C and D denote two clauses. If D is non-tautological and C D, then C⁺ subsumes D⁺ and C^– subsumes D^-.

PROOF.– As C⁺ is a sub-clause of C, every model of C⁺ is a model of C (because clauses are disjunctions of literals). The same reasoning shows that every model of C^– is a model of C.

C⁺ (respectively, C^-) is not auto-resolvent, as it only contains positive (respectively, negative) literals.

By application of theorem 8.1:

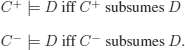
But C⁺ (respectively, C^-) can only be a sub-clause of D⁺ (respectively, D^-); hence,

C⁺ subsumes D⁺ and

C^– subsumes D^-.

THEOREM 8.3.– Consider two clauses C and D. If D is not ambivalent, then C D iff C subsumes D.

PROOF.– We assume that C D.

If D is not ambivalent, then it cannot be a tautology (because all its literals can be evaluated to F). Thus (theorem 8.2):

(*) C⁺ subsumes D⁺ and C^– subsumes D^-.

C cannot be auto-resolvent: that would require a predicate symbol, say P, to occur in C⁺ and C^-, but then (definition of subsumption and (*)), P should occur in D⁺ and D^-, which is impossible as D is not ambivalent.

Therefore, by applying theorem 8.1, we obtain:

C D iff C subsumes D.

REMARK 8.5.– For the same Prolog program, if we have two questions C and D, as they are both negative, theorem 8.3 applies; hence, we have a decidable test to know whether C D, meaning that it suffices to have answered to C to answer to D.

Theorems 8.1, 8.2, and 8.3 enable us to obtain the procedure D log-cons C? to test whether a clause D is the logical consequence of a clause C. As we mentioned in remark 8.4, this is an undecidable problem, so the procedure may not terminate (because to procedure “Consequence” that is used in procedure “D log-cons C?”).

EXAMPLE 8.7.– As mentioned previously, we will say that clause C subsumes clause D instead of: clause C θ subsumes clause D.

1) and

2) and

3) is relation a quasi-order, i.e. a reflexive and transitive relation?

1) No, take and

2) No, take and .

3) Yes.

reflexive: take : the identity: C C

transitive:

and

there exist such that and

therefore:

hence, there exists = ₂ o ₁ = ₁₂

such that i.e.:

DIGRESSION 8.1.– (ontologies and DL). Description logics are languages for ontologies. As we mentioned in section 1.2, an ontology can be defined as an explicit specification of a conceptualization. In other words, an ontology is a(n abstract) model of a part of reality (the world) that we are interested in. This part of reality is represented by pertinent concepts (properties) and by relations between these concepts. This in a formalizable language⁵.

Ontologies have naturally taken a very important place in computer science for different kinds of information-processing systems, and a privileged field of application is the semantic web.

In order for them to be useful, ontology languages must have some inference capabilities, in particular, to detect non-contradiction between concepts or their relations.

Why the name DL? The concepts that are relevant to the domain under consideration are specified by descriptions of atomic concepts using properties (unary predicates) and relations (atomic roles) (binary predicates). Logics because their semantic is defined in a similar way to that used in logic.

Constructors are the logical constants (see definition 5.1) and some types of quantifiers.

DLs generally offer the possibility to name (complex) descriptions, constraints about the inclusion of concepts, and assertions of properties and relations between particular objects (note the analogy with logic programming).

The subsumption algorithm permits us to detect the inclusion between concepts. The definition of subsumption corresponds to the one in definition 8.1: concept D is subsumed by concept C iff every instance (i.e. particular case) of D is an instance of C (for example, the man concept is subsumed by the animal concept).

DLs can also detect the (in)consistency (i.e. the contradiction (or noncontradiction)) of the set of assertions and definitions. The consistency (or inconsistency) of a set of assertions can be proved by exhibiting a model (or the impossibility of constructing one), the method of semantic tableaux is a tool that is naturally used to automate such a process.

DLs are closely related to modal logics (see section 10.3).

The syntax and semantics of DLs are defined using methods similar to those used for FOL, which is normal as most DLs correspond to decidable fragments of FOL.

As for any automated inference problem, the trade-off between expressive power and decidability (AND complexity of the decision algorithm) must be appropriately resolved for DLs.

8.3. Abduction

Aristotle viewed abduction as a specific kind of reasoning⁶. Much more recently, C.S. Peirce (19th Century, beginning of the 20th Century) identified abduction as a specific form of reasoning based on principles different from the standard principles such as deduction and induction (see section 8.4). He used hypothesis, hypothesis inference, abduction, and retroduction as synonyms.

He acknowledged the utility of abduction, but also the difficulty of its theoretical justification:

Now nothing justifies a retroductive inference excepts its affording an explanation of the facts.

Sometimes it is formalized with the following rule (which is incorrect from the point of view of deductive logic):

is an explanation of .

The intuitive reason why this rule is incorrect is clear. For example, we know that flu causes fever, but when we have a fever, it can be due to another illness.

Peirce clearly showed the importance of abduction in scientific reasoning (giving as a paradigm the discovery of Kepler’s laws).

We find fish fossils on dry land. We then suppose that, in the past, the sea used to cover the land. This explanation (obviously not certain and not unique) is generally added to a corpus of knowledge that attributes some weight to the explanation.

Abduction is analogous to what are called, in particular in mathematics, inverse problems; these are ill-posed problems: theorems are formalized and we wonder what axioms are necessary to prove these theorems (or we look for the parameters that make a law true).

8.3.1. Discovery of explanatory theories

The context: we have a theory or a repository of knowledge at our disposal (set of non-contradictory formulas, in particular, an empty theory).

We observe: particular events. Some objects have some properties or are related to other objects, these are the positive examples; other objects do not have some properties or they are not related to some other objects, these are the negative examples.

The problem: generate hypotheses that enable us to explain the observations, i.e. formulas from which the observations can be deduced.

This description corresponds exactly to the scientific work in natural sciences.

The justification of the method for the discovery of explanations raises very profound philosophical problems. There are considerable differences of opinion on the essential characteristics of scientific explanation.

Notation:

C (also noted K): theory or knowledge on the domain of the observed facts.

E⁺: set of positive examples ;

E^-: set of negative examples ;

H: set of generated hypotheses.

8.3.1.1. Required conditions

We give the three following formulations A, B, and C, which represent the conditions that are required of explanatory theories (as for the resolution method, means contradiction).

A:

1)

% Satisfiability a priori

2)

% Necessity a priori

3)

% Completeness with respect to E⁺

4)

% Consistency with respect to E^-

B (with E = E⁺):

1)

% The hypothesis explains the examples

2)

% The hypothesis is not in contradiction with the theory

3)

% The hypothesis is not redundant

4)

% The theory does not explain E (necessity of H)

C:

1) , i.e. for (at least one)

% The observed facts cannot be explained by the theory alone

2)

% H is not redundant

3) for all

% The negative examples (counter examples) cannot be explained by the addition of H

4) for all

% The addition of H enables us to explain the observed facts

Condition (4), which is sometimes formalized by:

corresponds to what is known in philosophy of science as the coherence theory of truth, of which one of the versions is: the truth of a (true) proposition consists in its consistency with a given set of propositions.

REMARK 8.6.– The relation of non-logical consequence () is used. Its treatment is not simple in FOL, where the set of non-logical consequences of a set of formulas is not recursively enumerable (if it were, FOL would be decidable).

The following example shows some peculiarities of abduction (meaning that the proposed explanations generally depend on the deduction strategy that is used).

EXAMPLE 8.8.– (abduction and strategies). We wonder whether clause 6 given below is a logical consequence of clauses 1-5. If this is not the case, what premises can be added so that 6 becomes a logical consequence of the new set of premises?

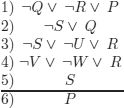
It is trivial to verify that 6 is not a logical consequence of 1-5 (counter example: {S, Q}, i.e. S and Q are interpreted to T and all other propositional symbols are interpreted to F).

To discover the desired premises, we apply resolution with two different strategies, which will lead to two different explanations.

Explanation-1: R.

(We cannot deduce R because that would require to eliminate either U or V and W, and all three of them are pure literals).

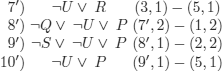
Explanation-2: U.

EXAMPLE 8.9.– (conditional answers). In logic programming, abduction could be used to give conditional answers when the program does not provide an answer.

Consider a program (often used as an example) that describes the characteristics of some animals.

and we ask the question

moves(john, y);

We give the execution tree:

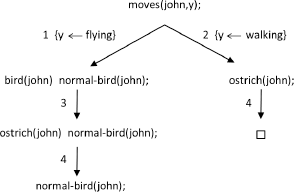
The unconditional answer (i.e. the standard answer) is thus:

moves(john, walking)

The conditional answer would be:

if normal-bird(john) then moves(john, flying).

8.4. Inductive inference

It seems like no one found a trace of an induction problem before the second half of the 17th Century. Induction seems to have been a problem forgotten in philosophy.

Now, the induction problem is unanimously recognized as an essential problem in knowledge theory.

There is currently a wide consensus to the fact that the induction problem was posed by the philosopher David Hume⁷.

Hume realizes that the information we have (that we receive, that impresses us) of the world is made of little fragments about the present or the past, and this is the only foundation that supports our general knowledge.

In other words, our data are made of particular facts.

Induction is a conjectural inference.

Etymologically: to lead → inducere → to let in → to bring

The first questions that come to mind:

– how can we, starting from particular experiences, establish laws that go beyond experience?

– can inductive inference be justified rationally?

These questions are very deep and habits often prevent us from analyzing them. If we are asked whether the sun will rise tomorrow, we will probably answer: “of course, as it has always been that way”.

But it is well known that it is delicate to make such generalizations, which are sometimes correct and sometimes incorrect. The following example (given by L. Euler (1707-1783)) shows what an incorrect inductive inference can be.

EXAMPLE 8.10.– (incorrect inference). We want to verify that, for 0 ≤ n ≤ 39, the polynomial n²+n+41 yields the sequence of prime numbers 41, 43, 47, 53, 61,….We may believe that we have found a formula allowing us to generate all prime numbers greater than 41. But this is only true for 0 ≤ n ≤ 39. For n = 40 we get: 40² + 40 + 41 = 41², which is obviously not a prime number.

Nevertheless, induction has an undeniable heuristic value, in mathematics, for example L. Euler stated that most properties on numbers had been discovered starting from the observation of examples and induction.

As the great mathematician Henri Poincaré said:

As in other sciences, mathematics can therefore proceed from the particular to the general.

By noticing the analogies between recursion and induction, Poincaré said:

Induction applied to physics is always uncertain, because it relies on the belief in a general order of the Universe, order that is outside of us. On the contrary, mathematical induction, i.e. proofs by recursion, imposes itself necessarily, because it is only the assertion of a property of the mind itself.

It is necessary to point out an essential difference with deductive inference.

8.4.1. Deductive inference

The conclusion is a logical consequence of the premises, we make explicit an information that was already in the premises.

8.4.2. Inductive inference

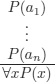
The conclusion is not a logical consequence of the premises. We add information to the conclusion that was contained in the premises:

– The justification of inductive inference is realized by an accumulation of particular cases, thus, the conclusion is only likely.

– Some authors say: “an argumentation is inductively strong if the truth of the premises makes the truth of the conclusion likely”.

There are also paradoxes.

8.4.3. Hempel’s paradox (1945)

A plausible principle is that logically equivalent hypotheses are confirmed with the same degree by the same experimental data.

All ravens are black

is logically equivalent to:

All objects that are not black are not ravens

By the plausible principle mentioned above, the observation of a white horse confirms the fact that all ravens are black!

DIGRESSION 8.2.– (on inductive inference). The presentation of inductive inference that has been made in section 8.4 is very concise and leads to the technique of inductive hypotheses generation proposed in section 8.5. In fact, it corresponds to the opinion of Aristotle who viewed induction as the act of getting from the particular to the general. This point of view is a bit restrictive and somewhat dated. Since the 17th Century, and even more so since the axiomatization of probabilities by Kolmogorov (1933), inductive and probabilistic methods have been closely related⁸.

We may wonder what the differences are between induction and abduction (see section 8.3). The boundaries between these two great classes of non-deductive reasoning are not very precise. However, it should be noted that induction corresponds to inferences in the context of uncertainty (the uncertainty of an event denoted by a proposition P is defined as the probability of P, whereas abduction corresponds to a theorization (C.S. Peirce), i.e. to the imagination of a theory that is explanatory for the phenomena that are observed and, if possible, predictive of new discoveries. probabilities provide clear foundations for induction but do not seem to be applicable to abduction.

Leibniz was the first philosopher of probability and the first to note that this theory could be used in an area of logic comparable to the theory of deduction. He incorporated probabilities into his theory of knowledge and anticipated what is known as inductive logic. He believed that the science of probability would become a new sort of logic, an idea that was taken up by J.M. Keynes⁹, H. Jeffrey, and R. Carnap in the 1920s. In this approach, it is accepted that there can be processes of non-deductive illustration, meaning that there can be good reasons to believe that a proposition P holds, without P being a logical consequence of other propositions. Carnap wanted to define an objective (and syntactic, i.e. exclusively related to the language that was used) measure of the degree up to which R is a reason for P.

By analogy with the notion of the proof of propositions that are logically necessary (deductive inferences are necessary)¹⁰, Leibniz proposed that the proof of a contingent proposition¹¹ P be an infinite sequence that asymptotically converges to P.

Inductive inference is ampliative (recall all the scientific discoveries that increase the field of what is known). Deductive induction is explanatory. From a classical point of view,¹² it is considered as not bringing any new knowledge: all the knowledge was already contained in the initial theory on which the inferences were carried out; the inference makes them explicit.

In other words, the information that is transmitted by deductive inference is void. A possible explanation for this choice is that P₁, P₂,... P_n C iff P₁ ∧ P₂,... ∧ P_n C is a tautology, and that it is admitted that the information transmitted by a wff (in a given language) is inversely proportional to the probability that the state of the world that it describes corresponds to reality¹³.

A more in-depth analysis of the concept of induction and the justification of inductive inference poses extremely difficult problems to philosophers of science. Several inductive logics (on which there is no consensus) have been proposed. J.M. Keynes characterized an inductive logic as a logic that studies “logical relations between two sets of propositions in cases where it is not possible to argue demonstratively from one to another”.

We have mentioned in section 8.4 what is called induction by enumeration, which must be distinguished from induction by elimination. Induction by enumeration permits us, starting from a sufficient number of facts, to obtain an inductive consequence (for example, all emeralds observed so far are green, therefore, all emeralds, including those not observed yet are green). Induction by elimination permits us, when enough alternate conclusions have been ruled out, to obtain an inductive consequence. This second form can be viewed as related to the advice by S. Holmes (see section 2.1.5.2) and to the usage of constraints (see section 9.2).

Some philosophers of science (in particular, K. Popper) defend the thesis that induction does not have its place in science, which they view as a deductive process based on hypotheses (theories) that scientists test using observable consequences. They can be falsified or rejected or temporarily accepted. These criticisms are mainly aimed at the forms of induction that have just been mentioned.

A form of induction that is frequently used is:

– the observed objects (i.e. the available evidence) that had property P also have property Q;

– by assuming that object a (that has not been observed yet) has property P;

– it is likely that a has property Q.

It is related to causal knowledge (laws of nature) and among the required conditions we can note: C is a cause of E if .

There exist different interpretations of the notion of probability¹⁴, among which the interpretation is known as logical or inductive (of which Carnap was the most important defender), according to which every set of facts E uniquely determines the probability of a hypothesis H and in which the conditional probability Prob(X | Y) is considered as a quantitative generalization of the logical consequence between propositions Y and X. The key notion in inductive logic uses the notion of confirmation and provides a framework for induction: a piece of evidence E confirms a hypothesis H at the degree , where m is a probability measure on the state of the world. The values c(H, E) = 1 and c(H, E) = 0 correspond to logical consequence and to incompatibility, respectively. c(H, E) > Prob(H), (where Prob(H) is the a priori probability of H) is a confirmation permitting us to learn from experience.

Proofs in such theories consist of the computation of the confirmation degree of pairs premises-conclusion.

Research on inductive logic is still carried out by researchers in philosophy of science, logic, and AI.

Of course, principles that relate (or differentiate¹⁵) the notions of deductive inference and of confirmation or verification have been searched for. One such example is the equivalence principle that was brought up in section 8.4.3 or the implication principle: if A confirms B then A confirms all logical consequences of B. But caution: if A is a logical consequence of C, then C does not necessarily confirm everything that is confirmed by A.

Imagine that the symptom denoted by proposition A is a confirmation that a patient has illness (denoted by proposition) M, but that the absence of the symptoms denoted by B and C allows us to reject the possibility that the patient has illness M. In other words, does not confirm M, although . The notion of confirmation is therefore non-monotonic (see definition 2.6). For this reason, inductive inference and confirmation must respect the principle of total evidence that imposes that all relevant evidence should be taken into account in each induction.

In the same way that we require deductive inference rules be correct (see definition 3.12), we may wonder how to distinguish good inductions from bad instructions, or those that are reliable from those that are not. According to Hume, a formal justification cannot be expected, as a deductive justification is impossible and an inductive justification would lead to a circular argumentation. However, if it cannot be justified, how can inductive inference be trusted? The answer that seems better adapted is that it is a probable inference. The law of large numbers that relates frequencies to probabilities can be viewed as setting the foundations of inductive inference (these laws are logical consequences of the axioms of probability theory and, although in empirical situations, additional hypotheses may be used, the inductive part of the reasoning depends on these laws that were established deductively).

8.5. Generalization: the generation of inductive hypotheses

This is a fundamental problem. Generalization is one of the efficient ways of obtaining knowledge of the world: to build a taxonomy, in learning, in causal connections, etc.

DEFINITION 8.3.– (generalization). A formula G is a generalization of a set of formulas F_i (1 ≤ i ≤ ⁿ) iff G F_i for all i.

For example, the discovery of a clause that subsumes another clause is a generalization. Subsumption is a weak form of logical consequence.

DIGRESSION 8.3.– Recent research in neurobiology and cognitive science has shown the importance for intelligent behaviors (in particular, logical reasoning) of inhibition mechanisms (of certain capabilities) that are used by the brain.

To make an analogy between the techniques presented above and the mechanisms that are used by human intelligence, the inhibited capability in generalization would be that of being able to distinguish details in the composition of sub-expressions.

Unification is useful in deductive inference:

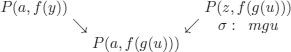
the mgu σ is the less instantiated unifier and is thus the greatest instance (i.e. the most general, starting from the mgu, all other unifiers can be obtained).

Generalization is useful in inductive inference:

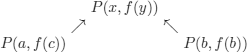
Here, the useful generalization is the most instantiated generalization, and it is therefore the smallest one, i.e. the least general; every other one can be reduced to it by substitution.

We may say that P(x, f(y)) explains P(a, f(c)) and P(b, f(b)).

Why are we searching for the least general generalization (lgg)? Because, in principle, we can always generalize by replacing complex expressions by variables…but this way of proceeding is too general and useless: the specificities of the studied phenomenon are lost, together with the possibility of discovering an interesting law relating its different particular cases.

DEFINITION 8.4.– (generalization of terms, literals, and clauses). (Note that this definition respects definitions 8.3 and 8.1, because in the case of literals, it is equivalent to requiring that G subsume F_i, and we know subsumption entails logical consequence (see exercise 8.1 (b)).

The lgg of a set of expressions is a generalization G_lgg, such that for every other generalization G, G is more general than G_lgg, meaning that there exists a substitution γ such that G_lgg = γG.

This concept can be applied to clauses. A clause C generalizes a clause D iff C subsumes D.

EXAMPLE 8.11.– The lgg of:

and:

is:

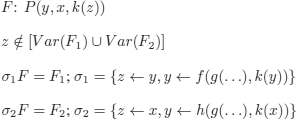
F': P(y, x, u) is also a generalization, but it is not lgg, as F = F′ with = {u ← k(z)}

EXAMPLE 8.12.– C₁: {Q(x) ∨ P(g(h(...)), h(...))}

the lgg of C₁ and C₂ is:

.

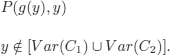EXAMPLE 8.13.– (explanation of concepts). An intelligent system has a knowledge base K, represented by logical formulas (clauses), about a graph. This knowledge was obtained from different agents (these agents may have used different names for the same concept).

K:

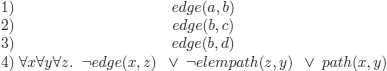
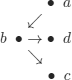
The system interrogates its environment to try to find an explanation of the concept of an elempath whose meaning it does not know, and obtains the following positive and negative examples:

E⁺:

5) path(a, c)

6) path(a, d)

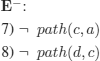
– We verify that K ∪ E⁻.

All the consequences of K ∪ E⁻ are:

– The set of all consequences of K:

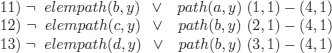
– The sets of consequences obtained are generally not finite. This example is a particular case in which the formulas do not contain any functional symbol.

– We search for the additional hypotheses that permit us to obtain E⁺ as a set of logical consequences of the new knowledge base.

H₁:

14) elempath(b, c)

15) elempath(b, d)

(14) and (15) permit us (resolution with (11)) to obtain (5) and (6)

Even better (from the point of view of the explanation):

H₂:

We try to produce clauses that relate known concepts to the concept we are trying to explain (here, elempath) and from which the possible explanation that was already obtained (H₁) can be deduced.

Candidates are:

The “best choice” seems to be:

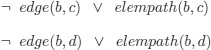
Because it enables us, by generalization (see definition 8.4), to propose the explanation:

which in English reads as: for all x and all y, if there is an edge from x to y, then there is an elempath from x to y, or, simply put, every edge is an elempath.

8.5.1. Generalization from examples and counter examples

In the generalization of terms, counter examples could also be used.

EXAMPLE 8.14.– (taking examples and counter examples into account). We assume given a signature (essential hypothesis) and examples: f (b, a), f (a, b), and f (a, c)

and counter examples: f(a, a) and f(c, c)

A generalization would be:

meaning: set of constant instances of f(x, y) such that x ≠ y (note that a constraint has been introduced).

REMARK 8.7.– The given representation is an implicit representation of the set of denoted terms, but does not give the form (structure) of these terms.

At least two questions arise:

– does there exist a finite explicit representation of denoted terms?

– is this representation computable?

EXAMPLE 8.15.– (of an explicit representation). If we consider the set of terms:

and we want to give an explicit representation for them, it is necessary to fix the signature of the corresponding Herbrand signature.

The set of terms

has the following finite explicit representation:

EXAMPLE 8.16.– (where there is no explicit representation). The set of terms:

does not have any finite representation on (for example) the signature:

The set of denoted terms is a proper subset (meaning that it does not contain the framed terms in (*)) of the set of terms on signature Σ:

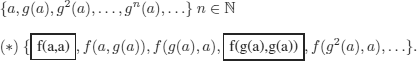
EXAMPLE 8.17.– (where the set of terms is empty).

on signature

denotes .

In the case in which an explicit representation can be provided, this information can be used for a more precise treatment of negation as failure.

EXAMPLE 8.18.– (of a “more detailed” treatment of NAF). The program

pp(f(a)) → ;
qq(f (X)) → not (pp(X)) ;

together with the question

qq(z);

will answer no.

Actually, we should obtain:

(the complement of pp(f(a)) on the implicit signature .

---

1 The resolution method is correct (see corollary 3.1), but we have only proved its refutational completeness (see exercise 3.34).

2 We can also imagine that we want to obtain all the consequences of a set of laws.

3 Which was considered from the beginning of modern science (for example, by Francis Bacon (1561-1626)) as being a part of the scientific method.

4 Note that an auto-resolvent clause is necessarily ambivalent, but that an ambivalent clause is not necessarily auto-resolvent, for example, P(a)∨¬P(b).

5 Note the similarity with, e.g. computer modeling, databases, object-oriented programing, etc.

6 Aristotle named abduction a syllogism in which the major was certain and the minor was only plausible.

7 It should be noted that induction is already mentioned in the treatise “Logic: or, The Art of Thinking”, published in 1662 during the emerging of probability theory: “We name induction, when the search for many particular things leads us to the knowledge of a general truth”.

8 It is worth mentioning, for example, that, in his work, R. Carnap aimed at clarifying the concepts of degree of confirmation, inductive logic, and probability.

9 The economist who wrote a treatise on probability.

10 Mathematical induction (see section 3.3.2) is to be classified among the methods of deductive inference.

11 Contingent: likely to be or not to be, to occur or not to occur.

12 Which is criticized by some logic philosophers.

13 This choice is consistent with information theory and with the property: if A B then P(B|A) = 1.

14 Although the axiomatization by Kolmogorov has become canonical.

15 Jacques Bernoulli (18th Century) was one of the first to notice the difference between deductive logic that is used in situations of certain knowledge and inductive logic, which is necessary in the situations of uncertainty that are encountered in everyday life. He seems to be the first one to have actually related probability to logic: he provided a numerical measure of arguments and spoke of the “strength of a proof’ or “degree of certainty”.