Chapter 2
A Few Thoughts Before the Formalization
2.1. What is logic?
We cannot give a formal answer to this question right away (we will get back to it though). In order to be understood, the answer would require some hindsight on the topic about to be studied.1
Try to understand what mathematics is about by only relying on its definition: mathematics, the science of quantity and space.
To choose an answer would not be very helpful right now, because a lack of criteria and references to concrete cases make it difficult to judge the pertinence of the answer.
A problem that is closely related to the one under consideration inspired the following thought to a famous philosopher (D. Hume):
The fact that ideas should logically entail one another is nothing but a fact, no more understandable by itself than any fact of the material world.
And this one from another less famous philosopher:
A logical formula is the expression of a natural phenomenon, as is gravitation or the growth of a tree.
2.1.1. Logic and paradoxes
Let us return to the history of logic and try to analyze some of the well-known concepts that are involved.
Logical difficulties arose very early in philosophy, religious “treaties”, and literature. Here are two examples:
– the liar’s paradox, due to Eubulides of Miletus (see digression 2.2): I am lying;
– the sentence: this sentence is false;
– the version of the liar’s paradox due to Epimenides of Knossos (6th Century BC): All Cretans are liars.
Are these really paradoxes?
What is a paradox?
Etymologically (15th Century AD): paradox: contrary to common opinion (doxa: opinion, from which originated heterodox and paradox).
Other definitions characterize paradoxes as argumentations (or assertions) that lead to a contradiction (logical paradoxes).
Paradoxes are sometimes associated with results (obtained by using correct reasoning) that are contrary to intuition and common sense, thus provoking surprise and perplexity.
One may also call a paradox a proposition that seems true (false) and is actually false (true).
Consider the following story (an excerpt from a masterpiece of universal literature):
A soldier is given the order to ask every person about to cross a bridge the following question:
(*) “What have you come here for?”
– If the person tells the truth, he is allowed to cross the bridge.
– If the person is lying, he must be hanged next to the bridge.
Someone arrives, and when asked question (*), shows the gallows next to the bridge and replies: “I have come to be hanged in these gallows”.
Imagine how embarrassed the soldier must feel, as he must either allow someone who lied to cross the bridge, or hang someone who was telling the truth!
There also exist paradoxes that occur in board games.
The rule Every rule has exceptions gives rise to problems. As it is a rule, it must admit some exceptions. Which means that there exist rules that do not admit any exception.
Here is another one:
i) The sentence below is false.
ii) The sentence above is true.
If (i) is T then (ii) is F hence (i) is F.
If (i) is F then (ii) is T hence (i) is T.
If (ii) is F then (i) is T hence (ii) is T.
If (ii) is T then (i) is F hence (ii) is F.
2.1.2. Paradoxes and set theory
Perhaps those paradoxes that had the most impact are those that involve set theory: probably because of the importance of set theory in mathematics, and particularly in the foundations of mathematics.
Bolzano introduced (in 1847) the notion of a “set” for the first time:
A set is a collection of elements the order of which is not pertinent, and nothing essential is changed by only changing this order.
But it is Cantor who developed set theory.
In naive set theory, according to Cantor, a set is:
Any collection of objects from our intuition or our thoughts, that are both defined and different.
…But allowing the use of any property to define a set can be dangerous:
There exist sets that do not contain themselves. For example:
The set of prime numbers < 150
There are others that contain themselves. For example:
The set of all ideas.
The catalog of all catalogs.
From a more abstract point of view:
The set of all sets.
It is simple to show that accepting as a set all the sets in the universe (U) leads to a problem.
If this is a set, it must contain itself. But the set of its subsets ![]() is also a set, and card
is also a set, and card![]() . Thus, there would exist a set containing more sets than the universe itself!
. Thus, there would exist a set containing more sets than the universe itself!
The set of all the sets that can be described in English by fewer than twenty words.
Bertrand Russell came up in 1902 with a “set” that leads to a paradox, which is known as “Russell's paradox”:
Let B denote the set of all sets A such that A is not an element of A (i.e. the set of all sets that do not contain themselves).
The existence of B leads to a contradiction:
– If B ![]() B, then B contains a set that contains itself (B), and B must not contain B (as B only contains those sets that do not contain themselves), hence B ∉ B.
B, then B contains a set that contains itself (B), and B must not contain B (as B only contains those sets that do not contain themselves), hence B ∉ B.
– If B ∉ B, then as B does not contain itself, B must contain B (as B contains all the sets that do not contain themselves), hence B ![]() B.
B.
Russell’s paradox was popularized as the “barber’s paradox”. A barber must shave every man who does not shave himself. How about him? Must he shave himself? If he does, then he is shaving someone who is shaving himself. Thus, he must not shave himself. If he does not shave himself, then he will not be shaving every man who does not shave himself. Hence, he must shave himself.
The origin of this problem is the axiom of abstraction (also called the axiom of naive comprehension): Given a property, there exists a set whose members are exactly the entities satisfying this property. In other words, for every predicate P, there exists a set whose elements are all the objects (and no other) that satisfy P:
![]()
2.1.2.1. The answer
The paradoxes on set theory were believed to be caused by the definition of incomplete objects as sets. Such objects should not be considered as sets.
When a set S and an object ob are defined in such a way that:
i) ob is an element of S;
ii) the definition of ob depends on S,
the definition is said to be impredicative (Poincaré). This is the same as what is commonly called a vicious circle.
To avoid paradoxes, impredicative definitions must be considered as illegitimate.
In set theory, this leads to the distinction between a class and a proper class.
A class: {x | P(x)} (P predicate symbol).
Sets are classes, but not all classes are sets:
{x | x ![]() x} (or {x | x ∉ x}) is not a set but it is a proper class.
x} (or {x | x ∉ x}) is not a set but it is a proper class.
Sets are complete entities.
Classes are incomplete entities.
In set theory, a constructive definition of a hierarchy of sets is provided (as usual, ![]() (X) represents the set of all the subsets of a set X):
(X) represents the set of all the subsets of a set X):
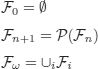
It is worth mentioning that impredicative but still important definitions are used in mathematics, such as the definition of the least upper bound (it is among all the bounds under consideration), maximum of a function on an interval (the maximum is among all the considered values), etc.
These kinds of definitions have also proved their value in computer science (communicating systems and streams).
A set belongs to a family of sets.
The axiom of choice (AC) and the continuum hypothesis (CH) are of great importance in set theory and in the foundations of mathematics.
We present three versions of the AC:
Version 1:
For every set X of non-empty sets y, there exists a function f with domain X, such that f(y) ![]() y for all y
y for all y ![]() X. (It is necessary to use this version only when X is infinite).
X. (It is necessary to use this version only when X is infinite).
Version 2:
Let S denote a set of paired disjointed, non-empty sets. There exists a set C containing exactly one element in each member of S.
Version 3 (formalization of version 1):
∀X∃f[f a function with domain ![]()
The CH states that between ![]() (the cardinality of
(the cardinality of ![]() and
and ![]() (the cardinality of
(the cardinality of ![]() , also denoted by
, also denoted by ![]() ), there is no other transfinite cardinal.
), there is no other transfinite cardinal.
The generalized CH states that the sequence of transfinite cardinals is:
![]()
The method used to construct this sequence is to consider a set and the set of its subsets. For ![]() (card
(card![]() ), the method is the one shown in exercise 3.1.
), the method is the one shown in exercise 3.1.
For the others, assume that there exists a bijection f between E and ![]() (E). By diagonalization (as in exercise 3.1), we can prove that f cannot be onto.
(E). By diagonalization (as in exercise 3.1), we can prove that f cannot be onto.
Gödel proved (in 1940) that if the ZF (Zermelo-Fraenkel) axiomatization is consistent (i.e. does not permit us to deduce a formula and its negation), then ZF + AC and ZF + AC + HC are also consistent. This means that AC and HC cannot be refuted.
Paul Cohen proved (in 1963) that AC and HC are independent from the other axioms in ZF, which means that AC and HC cannot be proved if ZF is consistent. HC cannot be proved in ZF + AC.
ZF and AC are undecidable in ZF.
DIGRESSION 2.1.– (sets and the AC in constructivism). For intuitionists or constructivists, or at least for most of them, a set E is well defined if and only if:
i) we are told how to construct an element of E;
ii) we are told how to prove that two elements in E are equal;
iii) we are given a proof that the equality defined in (ii) is an equivalence relation.
If only item (i) is satisfied, E is called a pre-set (it is possible to define sets, using pre-sets as a starting point).
A set E is completely presented iff for any of its elements, one can “read” evidence that it belongs to E (for example, ![]() is completely presented, as for every
is completely presented, as for every ![]() , it is possible to verify that m and n have no common factor).
, it is possible to verify that m and n have no common factor).
Constructivists consider the AC as essentially non-constructive; however, they accept some (constructive) versions that are provable in constructive mathematics (the name “axiom” was kept out of respect for tradition in classical mathematics). We provide the version named denumerable choice:
![]()
2.1.3. Paradoxes in arithmetic and set theory
EXAMPLE 2.1.– (Berry’s paradox). Consider the formalization of arithmetic based on Peano’s axioms (see example 3.8).
Let ![]() denote the set of all natural numbers that can be defined in English by a sentence containing at most a thousand characters (letters or separation symbols).
denote the set of all natural numbers that can be defined in English by a sentence containing at most a thousand characters (letters or separation symbols). ![]() is therefore finite, and there must exist natural numbers that do not belong to
is therefore finite, and there must exist natural numbers that do not belong to ![]() . The sentence:
. The sentence:
n is the smallest integer that cannot be defined by an English sentence containing at most a thousand characters
contains fewer than a thousand characters and defines a natural number n. Hence, n is a member of ![]() . However, by definition, n does not belong to
. However, by definition, n does not belong to ![]() .
.
We shall soon return to the notions of theory and meta-theory.
2.1.3.1. The halting problem
The idea underlying Russell’s paradox can be used to prove the undecidability (insolubility) of the halting problem. This idea can be characterized as the possibility for an expression designating an object to refer to a whole that the object belongs to.
The problem can be stated as follows:
Halting problem: given a program in a language (with the same expressive power as the Turing machine)2 and some input data3 (or an initial state of its input tape), decide whether this program (or Turing machine) halts or not.
To prove that this problem can be solved for a certain language, it suffices to provide a program that solves it.
Figure 2.1. The halting problem is unsolvable

However, to prove that it cannot be solved, it is necessary to use an indirect method (for example reductio ad absurdum).
It is possible to encode a program as a set of input data (see, e.g. section 5.9).
We therefore assume that we can write a program A, which decides for any program P whether P halts or not, i.e. A(P) returns true if and only if P halts.
We define the program D of Figure 2.1.
– Program D halts if D does not halt;
– Program D does not halt if D halts.
Contradiction. Hence A cannot exist.
DIGRESSION 2.2.– (on the importance of paradoxes). Paradoxes can be viewed as questions about the foundations of our reasonings, of our definitions, of our levels of language, etc. They have greatly influenced traditional logic, and also modern logic, set theory, etc. The principles of paradoxes can be used to obtain fundamental results in mathematical logic (for example Berry’s paradox and the proof of Gödel’s incompleteness theorem, see section 5.9) or in computability (the halting problem).
A typical historical figure that came up with several paradoxes is Eubulides of Miletus (circa 384-322 BC), who was contemporary with Aristotle, with whom he was at odds and against whom he produced several writings.
He is believed to be the father of eristic arguments (i.e. related to controversies, specious reasoning sophisticated quibbling).
It seems like the refutation of these arguments played a central role in the design of Aristotelian logic.
He is the one who came up with the liar’s paradox4, and that of the heap of sand (see example 8.1). The latter poses the problem of the relationship between the continuum and the discrete.
There also exist paradoxes (that are not necessarily logical paradoxes but do illustrate the etymology of the word “paradox”) in other scientific domains.
For example:
The paradox known as the Tocqueville effect: revolutions always start when a totalitarian regime becomes more liberal.
The Einstein-Podolsky-Rosen paradox involving quantum physics.
Bertrand’s paradox: one has to determine the probability that a randomly chosen chord in a circle is longer than the side of the equilateral triangle that admits the same circle as a circumcircle. Using the definition of Laplace (probability = number of favorable cases ÷ total number of cases) leads to two different values depending on the way one chooses to define the favorable cases. And both choices are equally reasonable.
2.1.4. On formalisms and well-known notions
G. Frege (19th to 20th Century) was one of the greatest logicians in history. He introduced the notions of formal systems, quantifiers, and proofs that are still used today.
The formalism he proposed was too cumbersome, as evidenced by the following examples.
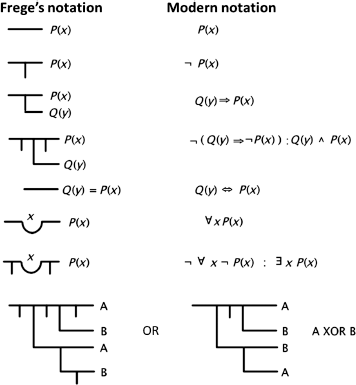
This formalism was not used very much afterwards (which is not surprising!)5.
We shall often ask ourselves questions about notions that seem natural. To convince ourselves that important problems are often hidden by our habits, it is enlightening to ponder, for example, on a word that can often be found in mathematical statements:
![]() … such that…?
… such that…?
1) According to formalists, existence means consistency, non-contradiction.
2) According to intuitionists6, existence means construction, meaning.
In mathematics that almost everyone uses, it is the first point of view that is more or less consciously adopted, although this notion may not be as natural as it may seem:
The following example, proposed by Frege, should make us think.
Consider the three following propositions:
– G is an intelligent being;
– G is ubiquitous;
– G is all-knowing,
and suppose that these three propositions as well as all their consequences are noncontradictory.
Can we conclude that G exists?
EXAMLPLE 2.2.– Do there exist irrational numbers a, b such that ab are rational?
Classical response: yes. Classical proof:
Take ![]() and
and ![]() , then:
, then:
![]()
(in the second case, ![]() .
.
This is not a constructive proof because no one can say which of the two possibilities proves the conjecture.
Here is a constructive proof
![]()
Note that, from a standard intuitionistic point of view, it is permitted to state in a proof that, for example, ![]() is a prime number or is not a prime number. This is because there exists an effective method that allows us to decide which of the two hypotheses is correct: it suffices to try all potential divisors.
is a prime number or is not a prime number. This is because there exists an effective method that allows us to decide which of the two hypotheses is correct: it suffices to try all potential divisors.
A (primitive) key concept of intuitionism is that of constructions. This concept can sometimes shake our beliefs about our understanding of mathematics.
The notion of construction appears to be inherent to every domain of study, and it may not be obvious to tell whether a proof is constructive. For example, consider the way Euclid proved that there exists an infinite number of prime numbers:
Assume that there only exists a finite number of prime numbers, and put these numbers in increasing order
![]()
pn is thus the greatest prime number. But in this case, p1 × p2 × … ×pn + 1 is also a prime number that is greater than pn. This is a contradiction, hence there are infinitely many prime numbers.
This proof method uses the law of excluded middle, but it also provides a way of constructing an infinity of prime numbers…
The following example, which was proposed by Brouwer, one of the founders of intuitionism, clearly shows the importance this school of thought attaches to what is known and not just to what is.
EXAMLPLE 2.3.– Let ![]() denote the position in the development of
denote the position in the development of ![]() , where the sequence 0123456789 occurs for the first time, and let n denote the integer defined as follows:
, where the sequence 0123456789 occurs for the first time, and let n denote the integer defined as follows:
![]()
If ![]()
![]()
![]() and
and ![]() is even, then:
is even, then:
![]()
If ![]()
![]()
![]() and
and ![]() is odd, then
is odd, then
![]()
However, we (still) do not know whether ![]() exists or not; we therefore have construction rules that we do not know how to apply. This definition only produces an approximation of n.
exists or not; we therefore have construction rules that we do not know how to apply. This definition only produces an approximation of n.
To quote the mathematician H. Weyl (another important figure of intuitionism):
To provide an existence proof that is not constructive is like announcing that there is a treasure hidden somewhere, without saying where it is exactly.
For intuitionists, the sentence ![]() is not valid for all assertions A. This does not mean that
is not valid for all assertions A. This does not mean that ![]() is false, as that would mean that a contradiction could be deduced from the sentence. Let A denote some mathematical conjecture. As long as A remains a conjecture, no one can state A, but as one cannot deduce a contradiction from A either, no one can state
is false, as that would mean that a contradiction could be deduced from the sentence. Let A denote some mathematical conjecture. As long as A remains a conjecture, no one can state A, but as one cannot deduce a contradiction from A either, no one can state ![]() .
.
2.1.4.1. Some “well-known” notions that could turn out to be difficult to analyze
a) Definitions and principle of the law of excluded middle
We are used to employing the law of excluded middle when carrying out a proof, especially for proofs involving reductio ad absurdum.
Yet there are some cases in which this use is problematic, especially from the point of view of a computer scientist or simply someone who is not content knowing that an object can be defined (this information by itself may not be that helpful), but also wants to know how this object can be constructed.
The following example should ring a bell to computer scientists, as it is related to the halting problem (or the impossibility of enumerating recursive functions).
EXAMLPLE 2.4.– Consider a sequence of integers amn, where m, n ![]()
![]() .
.
Let f denote the following function:
![]()
For a classical mathematician, this function is well defined, as for any given m (using the law of excluded middle), either amn = 0 for all n, in which case f (m) = 0, or there exists an n such that amn ≠ 0, in which case f (m) = 1.
But what if we want to actually compute the values of f (m)? Then it is necessary to examine an infinite number of terms: amn1,amn2,amn3…, which is of course impossible.
b) The notion of a proof
In classical logic, the meaning of the connectives ∧, ∨ and ![]() , is given by a combination of the truth values of the sub-formulas that are combined by these connectives.
, is given by a combination of the truth values of the sub-formulas that are combined by these connectives.
In intuitionistic logic, their meaning is a result of what should be considered as a proof of the formula containing these connectives. Here, a “proof” should be understood as a proof using correct means, and not necessarily a proof in a given formal system (see section 3.3 and remark 5.29).
– p proves A ∧ B iff p is a pair <r,s>,
r proves A and s proves B.
– p proves A ∨ B iff p is a pair <n,r>:
if n = 0 then r proves A; if n =1 then r proves B, which means that we are given a proof of A or of B, but we cannot tell which one it is7;
– p proves ¬A iff p proves A![]() ⊥
⊥
% ⊥: contradiction (this symbol is sometimes used to denote something undefined or false);
– p proves ⊥: impossible;
– p proves A ![]() B iff p is a rule q that transforms every proof s of A into a proof q(s) of B (together with any additional information that serves to convince that this is the case)8.
B iff p is a rule q that transforms every proof s of A into a proof q(s) of B (together with any additional information that serves to convince that this is the case)8.
First-order logic is introduced in Chapter 5, but for the sake of homogeneity, we introduce the rules corresponding to ∃ and ∀.
– A set X is completely presented if for all x ![]() X, one can examine evidence that x is indeed in X (see digression 2.1).
X, one can examine evidence that x is indeed in X (see digression 2.1).
– p proves ∃x ![]() X
X![]() (x) iff p is a pair <x,q>, where x is a completely presented member of X and q is a proof of
(x) iff p is a pair <x,q>, where x is a completely presented member of X and q is a proof of ![]() (x) (in other words, we explain how to obtain x).
(x) (in other words, we explain how to obtain x).
– p proves ∀x ![]() X
X![]() (x) iff p is a rule q such that, for all x
(x) iff p is a rule q such that, for all x ![]() X that is completely presented, q(x) is a proof of
X that is completely presented, q(x) is a proof of ![]() (x) (together with any additional information that serves to convince that this is the case).
(x) (together with any additional information that serves to convince that this is the case). ![]() (x) denotes a predicate on X, i.e. a rule that assigns to every element x
(x) denotes a predicate on X, i.e. a rule that assigns to every element x ![]() X that is completely presented, a well-formed formula (wff)
X that is completely presented, a well-formed formula (wff) ![]() (x).
(x).
REMARK 2.1.– (on intuitionistic logic). Intuitionistic logic is weaker (it admits less principles), but its theorems are more general (it requires less conditions).
c) Implication
Some of the choices that were made in classical logic sometimes lead to seemingly surprising results.
One such choice is material implication (as usual, T represents true and F represents false):

By randomly selecting two propositions p and q, the formula:
![]()
is a tautology (i.e. a formula that is always T).
Similarly, p ![]() (q
(q ![]() p) is also a tautology.
p) is also a tautology.
It becomes obvious that the definition of ![]() is too large.
is too large.
Another example that may throw a beginner off is that:
![]()
is not a contradictory formula (it suffices to choose p: F and q: F). The reason one may think it is contradictory is that, in mathematics, when considering a theorem, one is only interested in the case in which premises are T.
The implication connective ![]() has sometimes been criticized by logic philosophers as not being the adequate translation of if …, then …in natural language.
has sometimes been criticized by logic philosophers as not being the adequate translation of if …, then …in natural language.
In natural language, if …, then…is used to express, e.g.
– causality: if we put a kettle with water in it on top of a fire, then the water within will be heated;
– implication: if John is smaller than Peter and Peter is smaller than Mark, then John is smaller than Mark;
– (possible) explanation: if the flowers are on the floor, then someone must have dropped them.
On the topic of causality, it is important to note that material implication does not translate this notion adequately, at least for the three following reasons:
1) p ![]() p is a tautology, whereas causal connection is essentially irreflexive (this means no phenomenon is a cause of itself).
p is a tautology, whereas causal connection is essentially irreflexive (this means no phenomenon is a cause of itself).
2) A causal relation is essentially asymmetric (non-reversibility), which is not necessarily the case of ![]() :
:
p ![]() q and q
q and q ![]() p could both be true.
p could both be true.
3) p ![]() q is T if p is F and q is T. If p is the cause and q the effect, material implication would translate into the absence of a cause implies any effect.
q is T if p is F and q is T. If p is the cause and q the effect, material implication would translate into the absence of a cause implies any effect.
d) Translations in the language of logic
The word “and” is commutative, but is it always used in a commutative way?
I was hungry and I went to the restaurant.
I was ill and I went to see a doctor.
DEFINITION 2.1.– A unary predicate represents a property (small, mortal, etc). This property is the intension of the predicate.
The intension of an n-ary predicate (n > 1) is the relation represented by the predicate.
DEFINITION 2.2.– The extension of a unary predicate is the class of individuals that satisfy the property represented by the predicate. The extension of an n-ary predicate (n > 1) is the set of n-tuples that satisfy the predicate.
Usual mathematics puts the emphasis on extensionality.
Predicates with different intensions may admit the same extension.
We refer the reader to section 10.3 for an application of the concepts of intension and extension to computer science. The reader may also see examples 3.8 and 9.28.
DEFINITION 2.3.– A language is extensional iff any sentence in this language has the same truth value when one of its components is replaced by another component with the same truth value.
A connective is extensional if the truth value of composed propositions only depends on the truth value of their components.
Only using an extensional approach leads to a loss in the expressive power of the language.
EXAMPLE 2.6.– (a non-extensional language (R. Carnap)).
1) It is raining F % it is not raining right now
2) It is raining and it is not raining F
3) It is impossible for there to be ![]()
According to (2), the proposition in (3) (above the brace) has the truth value F.
Now, if we proceed as we are used to, and replace this proposition with another that has the same truth value (1), we obtain:
3′) It is impossible for there to be rain
This proposition obviously has truth value F.
Thus, the truth value of a composed sentence was changed by a replacement that does not pose any problem from the extensional point of view.
2.1.5. Back to the definition of logic
We return to the problem that we mentioned at the beginning of this section and enumerate some definitions of logic, knowing fully well that, as a great logician/computer scientist (D. Scott) once said:
(*) You have to know some logic to do some logic.
This is almost the same phenomenon as takes place when learning a natural language: there seems to be an innate underlying structure that limits the syntactic possibilities. The relationship between logic and biology was recently expressed by researchers in cognitive psychology in an article:
(If) logic is indeed the optimal form of biological adaptation…
Requirement (*) stated above may seem to be circular, but is a means of getting rid of an old paradox that has been tackled by philosophers (in particular by Plato) and that involves knowledge in general: we can neither search for what we know nor for what we do not know, because there is no need to search for what we already know, and what we do not know cannot be searched for, as we do not know what to search for.
This is what a contemporary philosopher calls the “that on which” as a region of pre-comprehension (prior discussion), as opposed to “what”, which is unknown.
In layman’s terms, one could say that principles cannot be postponed indefinitely, or that we cannot try to explain everything about a studied topic before studying it without risking an intellectual paralysis.
2.1.5.1. Some definitions of logic for all
Actual way of reasoning, in accordance or not with formal logic.
Abstract and schematic reasoning, often opposed to the complexity of the real world.
Consistent sequence of ideas, way of reasoning correctly, focus.
Reasoning: sequence of propositions related to one another according to determined principles and leading to a conclusion.
Etymologically:
– logic (13th Century): from the Greek word for “the art of reasoning”;
– reasoning: reason → to count → computation → ability to compute or reason.
2.1.5.2. A few more technical definitions
Logic studies what ensues from what.
Logic studies consistent sets of opinions (or hypotheses).
Logic is a science of truths.
Logic is a science of deductions.
Logic is a means to evaluate an argument9.
Logic studies the methods and principles that are used to distinguish between correct and incorrect reasoning.
At this point, an important question (which is mainly investigated by logic philosophers and psychologists) comes up naturally: why do we reason incorrectly? or why do we make mistakes when reasoning? This question is closely related to such epistemic questions as: what does it mean to reason correctly?, is the process of reasoning related to constraints from the physical world or to innate human characteristics (or to both)?, are the laws of logic revisable?, etc.
It has been noticed that most of the time, the mistakes humans make while reasoning are not logical mistakes, but those that result from a failure to use some of the premises, or their usage with a different meaning from the one they have in the problem statement, where the immediate perception overshadows the actual relation (i.e. the one that is of interest) between the objects under consideration.
A conceptual and technical remark. The notion of consequence has been widely studied from a formal point of view, contrary to that of non-consequence, which is as important10 (see section 8.3.1).
This notion is essential, e.g. for the identification of fallacious reasonings (some authors call these reasonings fallacies).
The area of study of formal logic is the analysis of sentences and proofs (the meaning of these words shall be made more precise later on, but their intuitive meaning is sufficient for the time being) by considering their form and by abstracting away their content.
We say formal logic (or mathematics) in contrast with philosophical logic (see section 2.2).
– Logic deals with all possibilities and views all possibilities as facts.
– The logic of certainty defines the domain of what is possible.
– A logic shall be designed to capture all patterns of reasoning that are meant to be characterized (this approach is necessarily an informal one).
A logic is a collection of mathematical structures, a collection of formal expressions and a satisfactory relation between these two collections.
Something particularly interesting to a computer scientist is the fact that in the past few years, a point of view on logic has steadily been imposing itself:
– modern logic is the foundational discipline for information science and it must be studied from the point of views of information, information processing, and information communication. It includes the study of inference, of computability, etc. Its different aspects are of a particular interest to mathematics, computer science and philosophy, and it is inherent to most of the subjects studied in AI.
This school of thought considers:
– inference as an activity that tries to use facts from the physical world to extract implicit information.
In the tree-like classification of the Mathematical Review, “logic and foundations” is at the same level as “set theory” and “number theory”.
Set theory is precisely one of the fundamental themes, and it is what one could call an “empirical” fact that all known mathematics can be based on it (for example with the so-called ZFC formalization, i.e. Zermelo-Fraenkel + axiom of choice).
Formal logic is necessary (at least) to rigorously state the axioms and to define the notion of proof.
On the topic of deductive reasoning, it is a common remark that one of the characteristics of practical or human reasoning is that the agent freely uses all available knowledge, whereas formal reasoning studies the (reliable) methods that verify that the conclusions are consequences of the premises (“logic is the study of what ensues from what”). Most logicians (as well as philosophers and cognitive psychologists) took an interest in the relationships between both ways of reasoning. It suffices to recall that Gentzen designed his natural deduction system so as “to set up a formal system that came as close as possible to actual reasoning”.
The fact that classical logic came short of modeling many characteristics of human reasoning, such as deficiencies of material implication, non-monotony, limited resources, failure to take time into account, etc., led from a theoretical and practical point of view to many very important developments, among which is non-classical logics.
One should finally notice that logic, as is the case for all other topics in science, changes with time in its fundamental principles, which can be interpreted differently as time passes by, in its methods, notations, topics of interest, etc.
DIGRESSION 2.3.– (formal definition of logic). We have given a few informal definitions of logic. They were enough to introduce the topic, but the reader who requires rigorous definitions may already be wondering: “but what is the formal definition of logic (abstract, i.e. independent from the way deductions are carried out)?”, and once more is known on the matter, the same reader will probably wonder “why are there so many logics?”
There is no formal answer to the second question, but a hopefully satisfactory answer might be that a given logic can be chosen because it is better adapted than another one, for example because it has more expressive power (it allows us to express more things), or because it allows us to say things more naturally, or because it is decidable, or easier to automate, etc.
We have answered the first question. The unifying notions are those of consequence relation or satisfaction (or satisfiability).
Here we introduce the notion of consequence relation. Returning to this definition after having worked on different logics will probably make it easier to grasp.
Algebraic methods play an important role in the definition of logic from an abstract point of view (they had already played an important role in the pioneering work of G. Boole).
DEFINITION 2.4.– (consequence relation (Tarski)). Let ![]() denote a formal language.
denote a formal language. ![]() is a consequence relation or operation iff it satisfies the following conditions for all
is a consequence relation or operation iff it satisfies the following conditions for all ![]() :
:
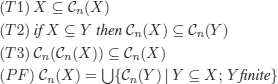
– Intuitively, ![]() maps a set of words from language
maps a set of words from language ![]() to the set (i.e. the union) of their consequences.
to the set (i.e. the union) of their consequences.
– (T2) must be discarded to capture so-called non-monotonic logics.
The notion of a consequence relation is the same as what is called closure operation in algebra.
DEFINITION 2.5.– (closure operation). Given a set E, an operation ![]() :
: ![]() (E) →
(E) → ![]() (E) is a closure operation iff for all X, Y ⊆ E:
(E) is a closure operation iff for all X, Y ⊆ E:
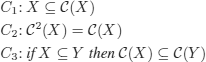
X ⊆ E is closed iff ![]() (X) = X.
(X) = X.
G. Gentzen (1909-1945) introduced a notion similar to that of Tarski with the following notation (see definition 3.11):
![]()
with the following informal meaning: the conjunction of the Pi’s(1 ≤ i ≤ m) admits the disjunction of the ![]() j’s (1 ≤ j ≤ n) as a consequence.
j’s (1 ≤ j ≤ n) as a consequence.
More generally, we may write:
![]() , where
, where ![]() ,
, ![]() are sets of words on a formal language.
are sets of words on a formal language.
DEFINITION 2.6.– (consequence relation (Scott)). Given a formal language ![]() , a relation
, a relation ![]() is a consequence relation in
is a consequence relation in ![]() 11 iff it satisfies the following conditions:
11 iff it satisfies the following conditions:
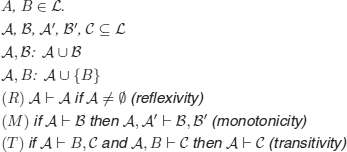
Thanks to properties (R), (M) and (T), ![]() can be viewed as a generalization of a partial order (see definition 3.23).
can be viewed as a generalization of a partial order (see definition 3.23).
It is fairly simple to show that a consequence relation à la Scott is a consequence relation à la Tarski, and conversely.
It is also fairly simple to prove that these relations coincide with the semantical notion of a logical consequence in definition 3.8.
We may now return to the question at the beginning of this digression and provide an answer.
What is an abstract logic?
Answer: a couple ![]() ,
,
where
![]() is a formal language
is a formal language
![]() is a consequence relation.
is a consequence relation.
The calculi that we shall study (semantic tableaux, resolution, etc.) are different implementations of a consequence relation.
REMARK 2.4.– Two oddities are worth mentioning: the existence of a journal named Informal logic, which deals with the study of fallacies and argumentations, and the fact that an author introduced (in 1957) the concept of infra-logic (which is closely related to fuzzy logic).
Logic allows us to analyze the relationships between objects, events, etc. without carrying out any experiment.
EXAMLPLE 2.7.– (What is of interest is the form)
1) All humans have a spinal cord.
2) All living beings that have a spinal cord are capable of acquiring conditioned reflexes.
3) Therefore, all humans are capable of acquiring conditioned reflexes.
has the same form as:
1) All pigs have four legs.
2) All living beings with four legs have wings.
3) Therefore, all pigs have wings.
Both reasonings are correct, although in the second one, one of the premises and the conclusion are unrealistic.
(1) and (2) are the premises of the reasoning and (3) is the conclusion.
EXAMPLE 2.8.– (…but one should be cautious)
1) I saw the portrait of Alexander Fleming.
2) Alexander Fleming discovered penicillin.
3) Therefore, I saw the portrait of the discoverer of penicillin.
has the same form as:
1) I saw someone’s portrait.
2) Someone discovered the wheel.
3) Therefore, I saw the portrait of the discoverer of the wheel.
The first is a correct reasoning, whereas the second is not.
EXAMLPLE 2.9.– (All the premises must be specified12).
1) I did not pay my estate tax in time.
2) Therefore, I will have to pay a fine.
From a logical point of view, the conclusion is erroneous, as there is no premise stating that those who do not pay their estate tax in time have to pay a fine (for example, maybe if this is the first time I am late, I will only receive a warning from the tax collector, etc.).
REMARK 2.5.– The usage of premises that are not explicit, which is due to bias or habits, and do not hold in the context of the discourse are a frequent (and unconscious) cause of fallacious argumentations.
We now consider a fundamental distinction.
2.1.5.3. Theory and meta-theory (language and meta-language)
We shall prove a precise definition of a formal theory in section 3.3, but we have already stated the basic idea here: a formal (or formalized) theory is a set of sequences of symbols (unless stated otherwise, we shall only consider finite sequences of symbols), called well-formed formulas (wffs) and some simple operations that can be applied to these sequences.
It is important to make the distinction between:
– what belongs to the formal theory;
– what concerns the formal theory, considered as a closed deductive system.
In other words, it is important to distinguish between:
– the object language (logic): theory;
– the observer’s language (logic): meta-theory.
![]()
are theorems in the theory, whereas the
duality principle: “replacing every ![]() (respectively
(respectively ![]() ) by a
) by a ![]() (respectively
(respectively ![]() ) in a theorem of set theory yields another theorem in set theory” is a theorem in the meta-theory, or a meta-theorem.
) in a theorem of set theory yields another theorem in set theory” is a theorem in the meta-theory, or a meta-theorem.
Confusing a theory and a meta-theory can have unfortunate consequences.
2.1.6. A few thoughts about logic and computer science
Before proceeding with the study of logic, using an approach that suggests the importance of logic by itself, and with the goal of showing that historically logic did not always have proponents13, we mention two thoughts about logic and refute one of them (in our opinion, the other one is simply a witticism made by a genius).
At a time when paradoxes were becoming increasingly popular, the great mathematician Henri Poincaré said:
Logic is no longer sterile, it generates contradiction!14
(It suffices to mention Gödel’s incompleteness theorem to fend off such attacks).
More recently, in a book written by two internationally renowned mathematicians (P. Halmos and S. Givant), we can read:
…the study of logic does not help anyone to think, neither in the sense that it provides a source of new thoughts nor in the sense that it enables one to avoid errors in combining old thoughts. Among the reasons for studying logic are these: (i) it is interesting in its own right, (ii) it clarifies and catalogues the methodology of mathematics, (iii) it has mathematical applications (for instance, in algebra, analysis, geometry, and set theory), and (iv) it is itself a rich application of some of the ideas of abstract algebra.
Of course, we agree with the four reasons given to study logic.
As far as the first sentence is concerned, we could also say (for example): linguistics never taught anyone how to speak.
From a more technical point of view, we can say that this vision is too restricted, in particular, it forgets that logic is a foundation for machines that help in thought operations (and therefore, that help to think). As a great French mathematician (A. Connes, recipient of the Fields medal) once said:
The verification process is extremely painful, because we are afraid we may have made a mistake. It is actually the most nerve-racking phase, because we cannot tell whether our intuition is correct… just as for dreams, intuition is easily mistaken. I remember having spent an entire month verifying a result: I would obsessively review every single detail of the proof, although this task could actually be entrusted to a computer which would verify the logic of the reasoning.
A convincing example of the utility of logic (especially when it is handled by computer programs) is the proof of an old conjecture by Kepler (on sphere packing). The proof of this conjecture was produced in 1998, thanks to human and computer means, it was 250 pages long.
Those specialists who analyzed this proof concluded that it was correct…with a degree of certainty of 99%! A project (expected to last several years) meant to produce (using a computer) a formal proof of Kepler’s conjecture was initiated in 2003.
Of course, logic does not claim (at least in principle) to capture all the operations of the mind (using images, discovery of regularities, causality, different kinds of analogies15, etc.).
2.2. Some historic landmarks
We cite some authors, among the most important, who contributed to the construction of Western logic (and thus of mathematical logic): Aristotle, Euclid, Leibniz, Boole, De Morgan, Frege, Whitehead, Russell, Tarski, and Gödel.
There is no written evidence of a theoretical presentation of logic before Aristotle. Before him (e.g. in Plato’s dialogs), there were argumentations, but we are not concerned with the way to carry out a debate.
The works of Aristotle on logic reached us within a collection of texts called Organon, which means “instrument” (Aristotle considered logic as a preparatory discipline).
He introduced syllogisms.
This term, which has been used in everyday language for a long time, globally identifies every rigorous reasoning that does not use any implicit proposition.
He proposed categorical syllogisms, which are forms of reasoning that exclusively rely on categorical propositions (see section 2.2).
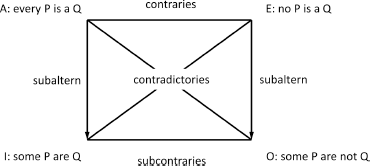
Aristotle considered four kinds of propositions (that were named categorical): universal affirmative propositions, universal negative propositions, particular affirmative propositions and particular negative propositions. The scholastics named them A, E, I and O, respectively (from Latin: AffIrmo et nEgO):

DEFINITION 2.7.– Two propositions are:
– contradictories iff they cannot be both true or both false;
– contraries iff they can both be false, but they cannot both be true;
– subcontraries iff they can both be true, but they cannot both be false;
– subalterns: a proposition Q is subaltern of a proposition P iff Q is necessarily true every time P is true and P is necessarily false every time Q is false.
We assume that there exist objects that satisfy property P.
For categorical propositions, this leads to the diagram known as the square of opposition, which establishes relations between any two categorical propositions:
The theory of syllogisms (syllogistic theory) is (generally considered as) Aristotle’s most important contribution to logic. Aristotle’s syllogistic theory was one of the pillars of logic for twenty centuries.
DEFINITION 2.8.– (syllogism) A categorical syllogism is an argumentation containing only propositions A, E, I, and O, with two premises and one conclusion, and containing three terms that each appear once (and only once) in exactly two propositions16.
If all birds are animals
and all sparrows are birds,
then all sparrows are animals.
Animals is the major term, birds is the middle term, and sparrows is the minor term.
REMARK 2.6.– The main problem in syllogistic theory was to distinguish between correct syllogisms (reasonings) and incorrect ones.
Aristotle classified reasonings into 256 possible syllogisms, 24 of which were correct.
The number 256 is simply obtained by enumerating all possibilities (Maj, Mid, Min, respectively, denote the major, middle and minor terms in a syllogism):
| Premise 1 | Premise 2 |
| (Maj-Mid) | (Min-Mid) |
| (Mid-Maj) | (Min-Mid) |
| (Maj-Mid) | (Mid-Min) |
| (Mid-Maj) | (Mid-Min) |
i.e. four possibilities.
For each of these possibilities, there are 16 possible combinations of the two premises: AA, AE, AI, AO, EA, EE, EI, EO, IA, IE, II, IO, OA, OE, OI, and OO.
There are also four possible conclusions (that correspond with the four categorical propositions). There are therefore 4 × 16 × 4 = 256 possible syllogisms.
REMARK 2.7.– During the 18th Century, the philosophies of Descartes, Locke, Hobbes, etc. led to the development of conceptions that were contrary to Aristotle’s philosophy, and to a loss of interest in syllogisms.
Leibniz rehabilitated Aristotelian syllogisms.
Syllogistic theory is still used nowadays (with a mathematical formalism). We have the following translations (see Chapter 5 and remark 5.27):
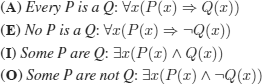
Below are some classical examples:
![]()
this corresponds to what is known as Barbara’s syllogism:
![]()
another syllogism:
![]()
Some reasonings, although considered as correct, cannot be identified so using Aristotle’s syllogistic. For example:
![]()
or:
![]()
A clue of the influence of Aristotelian syllogisms through time is the fact that in the 19th Century, machines that could automate these syllogisms were constructed.
Along with the notion of a syllogism, Aristotle17 defined the notion of a variable (see digression 3.3), and he formulated two laws:
– contradiction law: two contradictory statements cannot both be (simultaneously) true. This contradiction principle is the fundamental principle of thought according to Aristotle. He considers it the most unquestionable principle. It is the principle of being itself (Nobody could ever think that one same thing could be and not be), the most certain principle, and it is of course impossible to prove;
– law of excluded middle: if two statements are contradictory, then one of them must be true (there cannot be a third possibility)18.
The contradiction principle does not answer the question whether it is possible to know if a middle term between the assertion and the negation is possible. The law of excluded middle rejects this possibility19.
One may wonder what is the relationship between these two principles. According to Aristotle, the negation of the contradiction principle entails the negation of the law of excluded middle. But this does not mean that the law of excluded middle can be deduced from the contradiction principle. These are independent principles.
In logic, as in other domains in science, seemingly obvious principles become much less so when they are analyzed in detail. Consider the following proposition:
The Greek Aristarchus of Samos hypothesized in 250 BC that the Earth revolved around the Sun.
Intrinsically, (from an ontological point of view), this proposition admits either the value T or F, and can take no other value.
But what if we consider it from the point of view of what we know (epistemic point of view)? Most people would probably say they do not know whether it is T or F, and would rather assign it a third value: indeterminate (often denoted by ⊥). The method used to try to assign a truth value to such a proposition is fundamentally different from the one used to assign a truth value to propositions such as:
230402457 - 1 is a prime number.
or
7427466391 is the first prime number made of ten consecutive digits from the decimals of e.
Around 453-222 BC, a sect of Chinese preacher-monks, called Mohists (disciples of Mozi) came up with parts of a logic that was quickly forgotten.
As we have already mentioned, logic was influenced by Aristotle for a very long time. In the 17th Century, Kant stated that logic had not made a single step forward, and that it was finished and perfect. He also attacked formalization attempts, as he believed it was impossible to replace speculation by symbol manipulation.
Something similar took place for Euclidean geometry. Euclid was the first to propose what we now call, after a few modifications, an axiomatization. It was an axiomatization for elementary geometry. Until the discovery of non-Euclidean geometries (19th Century), this axiomatization was considered to be a completed model of the real world, and the only axiomatization to be coherent (or consistent).
Leibniz (17th to 18th Century) believed that logic could be transformed into a calculus (with all the advantages of working with symbols) that could be applied to all human activities.
Leibniz worked before Frege on the notion of a formal system.
Leibniz’s project was (at least partially) fulfilled by G. Boole (19th Century). One of his publications was a cornerstone of the separation of logic and philosophy. Boole discovered fallacies in philosophy books by using algebra.
De Morgan (19th Century) showed that it was impossible for all argumentations to be reduced to argumentations that exclusively relied on categorical statements.
Frege (19th to 20th Century) was inspired by Leibniz’s ideas, as the latter had developed a language for “pure thought”. He introduced formal systems (in their current form) and the theory of quantification. The symbolism he used was too cumbersome and was discarded later (we saw an example of his formalism in section 2.1).
Whitehead and Russell (19th to 20th Century) are the authors of the monumental Principia Mathematica and Russell is the author of the famous paradox that bears his name and that evidenced how dangerous it could be to allow a set to be defined by just any property (existence of contradictions in naive set theory, see section 2.1.2).
1 This remark is valid for any topic about to be studied.
2 Of course, leaving this language unspecified does not entail any loss of generality in the statement.
3 This can be any input data.
4 Legend has it that the poet and philosopher Philitas of Cos was subject to a deteriorating health as he tried to analyze this paradox.
5 One cannot overstate the importance of formalism. For example, McColl proposed P : Q as a notation for the implication P implies Q. But the symmetry in this notation suggests that P and Q have the same role…it is thus a bad formalism.
6 Some authors prefer to use the term constructivists (and constructivism), which they believe better mirrors the underlying philosophy. Brouwer, one of the founders of constructivism, viewed mathematics as the activity of carrying out constructions (a primitive and somewhat vague concept) in the mind of an ideal mathematician.
7 Strictly speaking, this condition is not necessary if the standard notion of a proof is used, as the problem “p is a proof of A (respectively a proof of B)” is decidable.
8 Some authors point out that this notion of a proof prevents the use of modus ponens (see section 3.3.2), when A ![]() B is one of the premises. Indeed, we would otherwise have an effective method for transforming a proof of A into a proof of B: it would suffice to apply modus ponens.
B is one of the premises. Indeed, we would otherwise have an effective method for transforming a proof of A into a proof of B: it would suffice to apply modus ponens.
9 An argument can be defined as a set of propositions, one of which is the conclusion while the others are premises.
10 As Sherlock Holmes would say: “When you have eliminated what is impossible, what remains must be the truth, no matter how improbable”.
11 Scott actually named the relation an entailment relation.
12 Some logics, especially some used in AI and called default logics do not have this requirement.
13 During the 4th Century, the Chinese thought that discursive reasoning was not a reliable way of grasping reality. In support of this statement, they cited the fallacious reasonings made by sophists, which led to conclusions that were obviously false.
14 Actually, he used the term “logicism” (which is one of the schools of thought in the philosophy of mathematics, to which is opposed, e.g. intuitionism).
15 It is worth mentioning that dogmatics (a school of medicine during the 2nd Century) used analogical inference, and that a theory of analogy was explored by scholastic logic (between the 12th and 15th Centuries).
16 It is common to use enthymemes, which are abbreviated syllogisms with only one premise (the other one being implicit) and a conclusion. For example (when speaking about someone), “he is moving, therefore he is alive”.
17 Some authors credit the law of excluded middle to Zeno of Elea.
18 We have already seen that for constructivists, this law cannot be applied to just any assertion.
19 We shall return to these two laws when we shall present logics other than classical logic (multi-valued logic, fuzzy logic).
