Chapter 4

First-order Terms

4.1. Matching and unification

4.1.1. A motivation for searching for a matching algorithm

Imagine that in example 3.9, you are given the first step of an alleged proof:

1)

without any justification, and that you (legitimately) wonder: “how can I be sure that this wff is a possible first step of a proof?”.

If formulas (structured strings) are represented as trees, answering this question reduces to finding what replacements should be carried out in the axiom schemas so as to find the desired wff (in a proof, this is the only possibility for the first step). We therefore try the axiom schemas one by one.

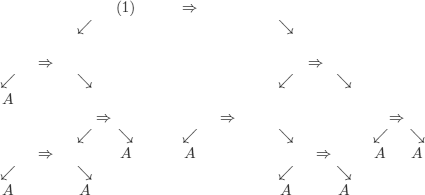
We will use X, Y, and Z for the meta-variables that appear in the axiom schemas to better emphasize that they are to be replaced.

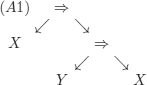
It is simple to see that there is no way to replace the variables in (A1) to identify (A1) with (1): we would need to replace X with A (rightmost leaf) and X with A ((A A) A) (leftmost leaf).

Let us try with (A2):

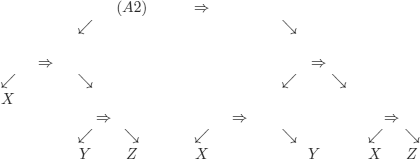
We realize that the trees (1) and (A2) can be identified by replacing:

As a conclusion, (1) can indeed be the first step of a proof in ₁.

In this example, we assumed that only one of the trees contained variables. Let us see what we would do if both the two terms to be made identical contained variables. In what follows, x, y, z,… denote variables (they are objects that can be replaced by other objects) and a, b, c,…, f, g,… denote constants (they are objects that cannot be replaced by other objects).

Since we want to design a general algorithm, if f, g,… denote function symbols, then we assume they do not have any particular property (associativity, commutativity, etc.).

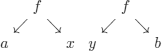
These trees can be made identical as follows:

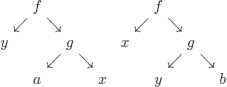
These trees cannot be made identical: we would need to assign y ← a and y ← b.

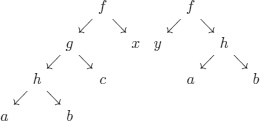
These trees can be made identical by assigning:

Trying to unify the following trees:

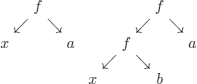
poses a problem. Which one?

4.1.2. A classification of trees

Finite trees

EXAMPLE 4.1.–

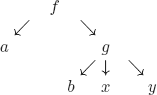
Rational infinite trees (i.e. with a finite number of subtrees)

EXAMPLE 4.2.–

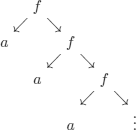
i.e.:

with a linear notation: f (a, f (a, f (a, …

Non-rational infinite trees

EXAMPLE 4.3.–

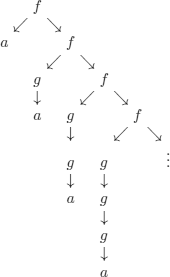
with a linear notation: f (a, f (g(a), f(g(g(a))), f(…

In the next section, we will formalize the concepts that have been introduced in an intuitive way.

4.2. First-order terms, substitutions, unification

Let:

denote a set of variable symbols;

= {x₁, x₂,…};

denote a set of function symbols, containing constants in particular, which are denoted by , .

An arity (n_i ≥ 0; i ≥ 1) is associated with every function symbol (representing the number of its arguments). Constants are of arity 0.

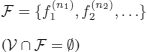
DEFINITION 4.1.– (terms). The set of terms constructed on , denoted by , is the smallest set such that:

1) if , then ;

2) if , then a ;

3) if and t₁, …, , then .

(Note that rule (2) is included in rule (3). It was added here for the sake of clarity).

Terms without any variable (i.e. ) are called closed terms.

REMARK 4.1.– Infinite trees are not terms.

Unless stated otherwise, we shall note variables u, v, x … and constants a, b, c,…

DEFINITION 4.2.– (variables, constants, depth of a term).

– The set of variables in a term t, denoted by V ar(t) or V (t):

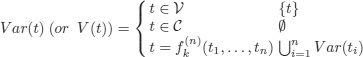
–The set of constants in a term t, denoted by Const(t):

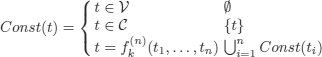
– The depth of a term t, denoted by Dpth(t):

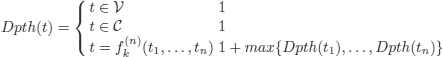
It was also possible to choose Dpth (t) = 0 in the first two cases.

DEFINITION 4.3.– (substitution).

– A substitution is an application:

which is the identity on all but a finite number of variables.

The domain of a substitution σ is the set:

and the codomain (or range) of a substitution σ is the set:

Substitutions are represented by the values of the variables in their domain:

or:

A substitution

is closed.

Given a substitution

σ is extended:

as follows:

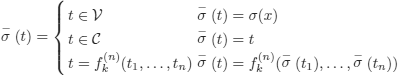
(It is standard to also denote the extension of σ by σ).

Equality is generally used in the sense of the identity, this is the case, for example, in:

(a + b)² = a² + 2ab + b² (the identity holds for any value of a and b), or it is used conditionally, this is the case for example in:

4 × x =16 × y, where only some values (possibly none at all) satisfy the equality.

Furthermore, when there are many solutions, some are more interesting than the others. For example, if we are interested in the solutions of the equation above that are positive integers, then {x = 4, y = 1}, {x = 8, y = 2}, {x = 12, y = 3}, … are solutions.

The most general solution is {x = × y; .

Notation: to emphasize that this is a conditional equality, we shall write , and if terms are involved, we shall write .

These comments are a motivation for the following definitions.

DEFINITION 4.4.– (ordering on substitutions). A substitution a is more general than a substitution γ iff there exists a substitution λ such that , where o denotes the composition of substitutions (i.e. of functions).

DEFINITION 4.5.– (unification). Given the equation , where , the unification problem consists of finding the most general unifier (mgu) such that:

σ(t₁) = σ(t₂) (syntactic identity).

If only one term contains variables, (say t₁), the problem that consists of finding a σ such that

is the matching problem.

Notation: we often denote by mgu(t₁, t₂) the mgu of t₁ and t₂, and we write σt instead of σ(t).

The unification algorithm either constructs the mgu of a set of term equations or detects that there is no solution.

EXERCISE 4.1.–

a) Find the solution (if it exists) of equation:

b) Find the solution (if it exists) of equation:

c) Given the substitutions

and

Construct the substitution .

d) Consider the equation where

Is the cycle rule of UNIFICATION still necessary? Could you give a sufficient condition guaranteeing the cycle rule is not needed?

EXERCISE 4.2.– In a calculus called the equivalential calculus, the wffs of the language are of the form e(X, Y), where e is a constant symbol (that stands for equivalent), and X, Y (meta)variables that denote wffs of the language (such as A, B, C in S₁; see section 3.4).

The only inference rule is:

Question:

Given two wffs

e(X, e(X, e(Y, Y))) and

e(Z, Z)

1) Can CD be applied?

2) If so, what are the possibilities?

3) If CD can be applied, what is(are) the direct consequence(s)?

EXERCISE 4.3.– The algorithm Unification does not assume any property on the functions under consideration, and produce a unique result (substitution), up to a renaming of the variables.

If we assume that (some of) the binary functions under consideration are commutative, for example:

Can you modify the algorithm Unification to take this property into account?

For example, for equation:

UNIFICATION would return ⊥, but once modified, when f and g are commutative, it should produce two solutions:

REMARK 4.2.- Considering function symbols that denote functions with certain properties can turn out to be very complex. For example, if f denotes an operation (function) that is associative-commutative, i.e.

then the equation

has the following solutions:

and others.

It is simple to verify that we cannot transform one of these unifiers into another by applying a substitution (as previously). We will keep in mind that the solutions are no longer unique (and there can be many of them).

The following exercise is an example of how the unification algorithm can be adapted to treat data other than terms, by expressing this data as terms and using some ad hoc conventions.

EXERCISE 4.4.- Use the algorithm unification (that was modified in exercise 4.3) to show that, if the unconditional premises (i.e. those that do not contain ) are literals, then the rules MP (modusponens) and MT (modus tollens):

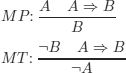
are particular cases of the resolution rule: