Chapter 9

Problem Specification in Logical Languages

9.1. Equality

Equality is an extremely important¹ predicate (relation), in particular, in mathematics, that has a meaning in every universe of discourse, which is not the case for other predicates (for example, if P(x, y) has the intended meaning “x loves y”, it would have no meaning if the universe of discourse was, say, ).

It seems natural to want to treat it using logics that we have already studied.

Imagine we have to prove the validity (or non-validity) of the equivalence:

If propositional logic (PL) is used, using the names mentioned, we get , which is obviously a non-valid formula, but our experience with = tells us that formula (*) is valid, and we want to classify it as such.

FOL would also fail (without any additional axioms) to capture the characteristics of equality.

Equality has particular properties that we must make explicit.

There are formulas such as:

that are valid when R is replaced by x = y or by any other predicate Q(x, y).

But the validity of the formula

depends on the semantics of =.

9.1.1. When is it used?

EXAMPLE 9.1.– There exists a unique element with property P:

i)

or:

ii)

(i) and (ii) are often abbreviated

There are at least two objects with property P:

iii)

There are at most two objects with property P:

iv)

There are exactly two objects with property P:

v)

It is clear that:

(iii)

9.1.2. Some questions about equality

1) Why is equality needed?

2) What is equality?

3) How can we reason with equality?

9.1.3. Why is equality needed?

Since:

– everything is identical to itself and to nothing else.

– identifying a thing to itself is trivial and identifying it to something else is false.

Where does the need for and usefulness of equality come from?

From the fact that we allow different names for the same object.

(It is not the names that are identical, but the named objects).

9.1.4. What is equality?

Equality is an equivalence relation with the replacement or substitution property. To formalize the equality between two objects, Leibniz expressed (Leibniz’s law)²

Leibniz’s law is sometimes presented as the conjunction of the two following laws (the first is the common law in mathematics):

Substitution principle (indistinguishability of identity)

Indiscernibility principle (identity of indiscernibles)

(Leibniz’s law is not a wff of FOL).

Axiomatization of equality:

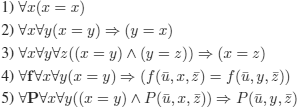
where and , respectively, denote u₁,…,u_m and z₁,…,z_n (0 ≤ m, n) (Of course, here we assume that f and P are of arity m + n + 1).

Note that (4) and (5) are not wffs of FOL (which does not allow for the quantification of function or predicate symbols). Therefore, equality cannot be defined in FOL, and of course, it cannot be defined in PL either.

However equality can be treated in FOL.

When treating formulas that contain equalities in FOL, the latter can be axiomatized in this particular setting simply by noticing that in every wff of FOL, there are finitely many predicate and function symbols. Formulas (4) and (5) can be written for each of these symbols.

This means that we need to add:

formulas,

where:

n_f: number of functional symbols in the formula;

n_p: number of predicate symbols in the formula;

ar_fi: arity of function f_i; and

ar_pj: arity of predicate pj.

REMARK 9.1.– Equality can be axiomatized with (1), (4), and (5) (see exercises 9.1 and 9.2).

EXAMPLE 9.2.– We want to reason on the set of clauses S below:

1) P(f(a), g(e))

2) ¬P(f(x), g(x))

3) f(a) = f(b)

4) b = c

5) e = c

We add the clauses:

(recall that: P ∧ Q R⇔¬P ∨ ¬Q ∨ R)

6) x = x

7) ¬(x = y) ∨ (y = x)

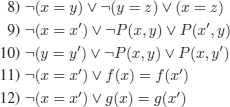
Of course, we could have written equality as an ordinary predicate with the prefix notation: E(…,…), but we prefer the standard mathematical notation.

REMARK 9.2.– Substitution seems natural, in fact it is natural for extensional languages. This is not the case for non-extensional languages.

Consider the following sentence:

i) Michael knows that the sum of the first n odd numbers is 1 + 3 + 5 + … + (2 × n + 1).

The sentence:

ii) If Michael knows that the sum of the first n odd numbers is 1 + 3 + 5 + … + (2 × n +1), then Michael knows that the sum of the first n numbers is

is trivially true (it is actually a tautology).

Furthermore,

iii) 1 + 3 + 5 + … + (2 × n + 1) = n².

Using (iii) and substituting by n² in (ii) leads to:

iv) If Michael knows that the sum of the first n odd numbers is 1 + 3 + 5+ …+ (2 × n + 1), then Michael knows that the sum of the first n odd numbers is n².

…and what used to be a tautology does not remain so, because Michael may not be aware of property (iii).

9.1.5. How to reason with equality?

It is possible to handle equality by resolution, by axiomatizing it (see the following section) or using the paramodulation rule (see definition 9.1).

The following example shows that it is sometimes possible not to bother about equality in the statement of some problems (here, a theorem). The way of proceeding is the way used in logic programming (see Chapter 6), where a key technique is the naming technique.

9.1.6. Specification without equality

EXAMPLE 9.3.– (a theorem in group theory, without =). We prove the following theorem (see also example 9.13) by resolution:

If in a group G we have: ∀x.x² = x, then G is commutative.

The associativity of an operation o is expressed by:

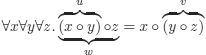
By naming as indicated by the braces, we can express the associativity of o using the predicate:

P(x, y, z): the composition of x and y yields z.

We thus express with clauses: x o v = w iff u o z = w

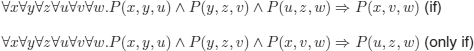
Identity will be denoted by the constant e and the inverse of an element x by i(x).

The conclusion of the theorem (i.e. commutativity):

and its negation:

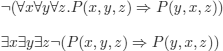
after Skolemization, we obtain two clauses:

Proving the theorem therefore boils down to deducing 2 from clauses (1) to (9) below:

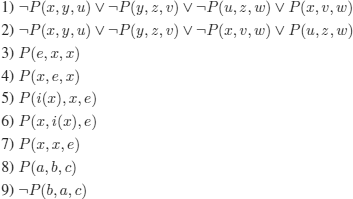
We shall use the hyperresolution rule without having defined it formally; it corresponds to applying several resolution steps in one single step.

9.1.7. Axiomatization of equality

Once it has been axiomatized, equality is a predicate like any other predicate, and its definition can be incorporated by adding formulas to the problems that use it, and then using the method of semantic tableaux or of resolution. The goal is to extend these methods. Of course, here, extension means incorporating rules that take the properties of = into account into these methods.

9.1.8. Adding the definition of = and using the resolution method

EXAMPLE 9.4.– We give a linear refutation by resolution, for the set of clauses S of example 9.2:

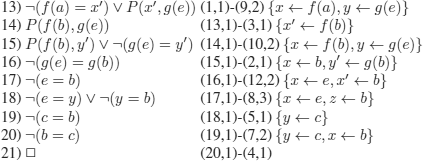
REMARK 9.3.– Equality is not handled by Prolog, in which it is possible to use the predicate eq that can be evaluated (see exercise 6.10).

To convince oneself that the predicate does not correspond to equality, it suffices to use the program (aa, bb, and cc denote constants):

and to ask the question:

The answer will be “false”, which does not correspond to the answer we would get with the usual notion of equality (that was formally defined in section 9.1.4).

REMARK 9.4.- Reasoning automatically with equality can be very difficult. If one is interested in reasoning only on finite domains, problems can often be formulated in such a way to avoid its occurrence, as shown in the following example.

EXAMPLE 9.5.- We assume that there is a set of candidates to a set of available jobs, and we want to express that there cannot be two candidates who get the same job.

The wff of FOL with equality (FOLE or FOL=) correctly formalizes the statement of the problem.

where R(x, y) means: job y is given to candidate x.

Once the number of candidates has been fixed, say Alice (a), Bob (b), Carrie (c), and Daniel (d), we can express the statement (*) (with the objective of not having to handle equality) with the six (i.e. ) following clauses:

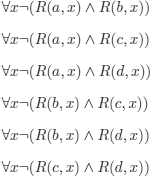
9.1.9. By adding specialized rules to the method of semantic tableaux

The following assertions are implicitly accepted in general, but deserve to be restated:

– names (constants or terms without variables) denote an object that exists. This assumption is necessary to be able to adopt the (quite natural!) point of view admitting that a ≠ a (i.e. ¬(a = a)) is contradictory;

– function symbols denote total functions, i.e. if f is an arbitrary function symbol and a is a constant, then f(a) = b, where b is a constant denoting an object that exists, as recalled above.

:

If a branch B contains , where is an n-tuple of closed terms: put a x in B.

:

For every constant (or term denoting a constant) and every closed formula, use substitution (axioms 4 and 5 in the axiomatization of equality).

REMARK 9.5.– To avoid strategies that would artificially introduce non-termination, we will require that the closed formulas produced by substitution do not already occur in the branch (the same remark as for universal quantifiers).

Do we need to add rules that handle symmetry and transitivity?

If it is possible to prove the validity of these axioms using and , then we will have answered “no” to the question and we will be done with the extension of the method of semantic tableaux incorporating equality³.

EXERCISE 9.1.– (symmetry of =). Prove, using the method of semantic tableaux extended with and , the validity of:

EXERCISE 9.2.– (transitivity of =). Use the method of semantic tableaux extended with and to prove the validity of:

.

We can therefore extend the method of semantic tableaux with and , and it can be applied to FOLE (FOL=).

We easily obtain the procedure to do so (the added lines are preceded by =).

EXERCISE 9.3.– Use the method of semantic tableaux with equality to prove the assertion of example 9.1, i.e. (iii) ∧ (iv)⇔ (v).

9.1.10. By adding specialized rules to resolution

9.1.10.1. Paramodulation and demodulation

These rules were introduced to handle reasoning on clauses that contain literals involving equality.

We first study the paramodulation rule. It permits us in one step to combine the following operations:

– instantiation: replacement of variables by terms;

– replacement of equals by equals.

For example, if we have the two clauses (1) and (2) below:

1) f(x) = g(a) % recall: for all x

2) f(b) = c

from (1) we may deduce:

3) f(b)= g(a)

and, using (3) and replacing equals by equals in (2), we obtain:

2) g(a) = c

DEFINITION 9.1.– (paramodulation rule). We note:

L[t]_u: term t occurs at position u in literal (or term) L.

L[t]: term t occurs at an unspecified position in literal (or term) L.

L[u ← t]: the literal (or term) obtained by replacing the term occurring at position u by t.

Consider two clauses C and D:

C: s = t V C₁

D: L V D₁

where:

L: a literal (in particular, an equality or the negation of an equality).

C₁, D₁: clauses.

If L[r]_u and r s admit a solution , then the clause

is a paramodulant of C in D.

EXAMPLE 9.6.–

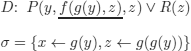
A paramodulant of C in D is the clause:

EXAMPLE9.7.– Prove, using the paramodulation and resolution rules, that the set containing the three clauses below is E-unsatisfiable (i.e. if the predicate =, denoted here in infix mode as usual, represents equality).

REMARK9.6.– (reflexivity must not be forgotten). Although it is not necessary in this example, when reasoning with equality, it is necessary to add the clause:

in order not to lose refutational completeness.

Otherwise, it is impossible to prove by resolution and paramodulation that the set of clauses {a ≠ a} is contradictory.

If we add x = x, then, by resolution, we obtain with {x ← a}.

EXAMPLE 9.8.– Prove, using the paramodulation and resolution rules, that the set consisting of the four clauses below is E-unsatisfiable (i.e. S is unsatisfiable when = is interpreted as the usual equality, see section 9.1.4).

Demodulation or rewriting or reduction uses equalities to replace terms by “simpler” terms, we thus need complexity measures, and if, for example, we consider brackets on the right as simpler, we orient the equality (x + y) + z = x + (y + z) as (x + y) + z → x + (y + z).

The goal is to keep information in its simplest form, if possible a canonical form. For example, a + 0 → a. This, thus, corresponds to algebraic simplification (symbolic computation).

EXAMPLE 9.9.– a) When considering the unit clause:

oriented into:

the clause:

is demodulated into

P(g(a), b) and removed.

b) When considering the unit clause:

x + 0 = x

oriented into:

x + 0 → x

the clause:

P((a + 0) + b, c)

is demodulated into

P(a + b, c) and removed.

DEFINITION 9.2.– (demodulation rule). We write:

L[t]_u: term t occurs at position u in literal (or term) L.

L[u ← t]: is the literal (or term) obtained by replacing the term at position u by t.

Consider the two clauses C (unit, with equality as a predicate) and D:

C: s = t the demodulator

D: L V D₁

where:

L: literal (in particular, an equality or the negation of an equality).

D₁: a clause.

If L[r]_u and there exists a substitution σ such that σs = r (matching instead of unification),

then the clause

σ(L[u ← t] V D₁) that replaces D

was obtained by demodulating D with C.

EXAMPLE 9.10.– (is demodulation complete?). The answer is no, as shown in the following example:

S is E-unsatisfiable, but a natural complexity measure would orient the equalities f(c) → a; f(c) → b and it would be impossible to derive a contradiction.

EXAMPLE 9.11.– (what if = occurs in non-unit clauses?). The E-unsatisfiable set of clauses (1) to (4) below shows that restricting the usage of = to its occurrences in unit clauses is too strong a requirement (meaning that unsatisfiable sets of clauses are not detected as so, and completeness is lost).

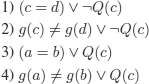
S is E-unsatisfiable, a result that is easily proved by resolution, by axiomatizing equality with the technique that was already presented. We add:

and we obtain:

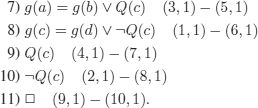
EXAMPLE 9.12.– (demodulation: a canonical procedure?). The answer is no. Consider the clause:

(*) Q(f(f(a, b),c))

and the set of demodulators:

1) f(a, b) → d

2) f(b, c) → e

3) f(f(x, y), z) → f(x, f(y, z))

By using (1), (*) can be demodulated into:

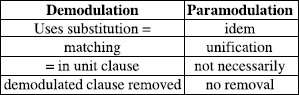
i) Q(f(d, c))

By using (3), (*) can be demodulated into:

Q(f(a, f(b, c)))

and (2) into:

ii) Q(f(a, e))

(i) and (ii) are two equivalent clauses, but one cannot be reduced to the other by demodulation.

Figure 9.2 summarizes the differences between demodulation and paramodulation.

EXAMPLE 9.13.– (a theorem in group theory). If in a group G, ∀x.x² = e, then G is commutative.

A human would probably give a proof similar to the following (of course, o denotes the operation in G):

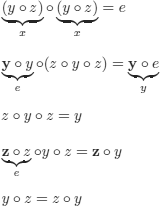
Another human proof (using another strategy) could be:

hence ((1) and (2))

To give a proof by paramodulation, demodulation, and resolution, the group axioms (which are implicit in the proof above) need to be written in clausal form, and the conclusion must be negated:

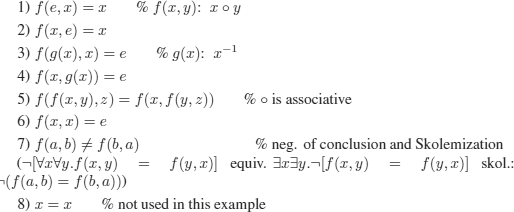
Paramodulation of (5) into (6):

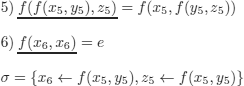
We obtain (after renaming the variables):

Paramodulation of (6) into (5):

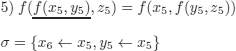
we obtain:

Demodulation with (1):

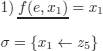
We obtain (after renaming the variables):

Paramodulation of (9) into (10):

The paramodulant is:

Demodulation with (2):

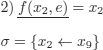
We obtain (after renaming the variables):

Paramodulation of (11) into (10):

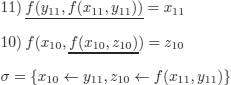
The paramodulant is:

We obtain (after renaming the variables):

Resolution

13).

9.2. Constraints

The notion of constraint is very natural and appears in many different situations.

Compared with the other notions that have been studied, it is best related to those of logical consequence and subsumption. For example, a theorem that holds for groups is more general (i.e. is valid for more objects) than a theorem that holds for Abelian groups that have the additional property of being commutative. If a theorem holds with less constraints on its hypotheses, then obviously (monotony, see exercise 3.13 c), it also holds with more of them (subsumption)⁴.

The premises of the theorem can be viewed as constraints and the conclusion as the solution of the constraints (the conclusion holds under the constraints of the premises). Every model of the premises (and maybe more) is specified by the formula in the conclusion (equivalent to the logical consequence).

You have already been confronted many times with this notion in a concrete way, for example, in the problem of coloring a graph with the constraint that this must be done with three colors and that two nodes connected by an edge must not have the same color (see example 9.19).

A constraint is a condition to satisfy. The domains (i.e. the sets of possible values for the variables) give their names to the types of constraints. The most studied ones are arithmetic constraints, Boolean constraints, constraints on strings, constraints on trees ((dis-) equations on terms), and constraints on finite domains.

The main problems that arise are:

– satisfiability (does there exist a solution?);

– equivalence/implication between constraints;

– simplification;

– optimization.

DEFINITION 9.3.– A wff of FOL of the form:

(or a set

with predicate symbol

is called a constraint.

Var() = V

Given a domain (set) D, the problem of finding a substitution:

enabling us to evaluate to true is called the problem of constraint solving.

The projection of a constraint C on a set of variables is a constraint C_P with Var, such that:

– if σ is a solution of C, then σ is a solution of C_P ;

– if dom and σ_R solution of C_P, then there exists an extension of σ_R to Var(C) that is a solution of C.

The definition of a projection simply means: “we only deal with the subset of constraints containing some given variables of the problem”.

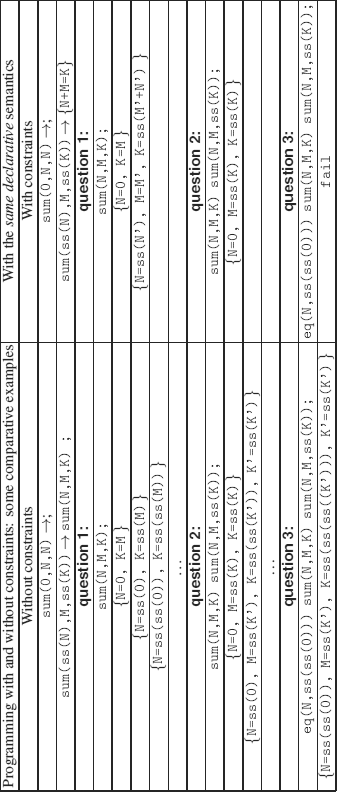
The procedure PLC specifies the abstract interpreter that permits us to handle clauses with constraints. We give a few examples on using constraints in a logic programming language (Prolog 3).

EXAMPLE 9.14.– (logical connectives). Assuming that we do not have Boolean constraints (although we do), we want to define the usual logical connectives (see section 3.1) as arithmetic operations, using arithmetic constraints, and encoding T by 1 and F by 0:

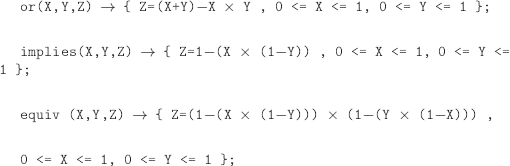
Of course, could have been written:

implies (X,Y,Z)→ {Z=1 - X + X × Y, 0 ⇐ X ⇐ 1, 0 ⇐ Y ⇐ 1} by either transforming the constraint or directly using the equivalence (X Y) ⇔ (¬X ∨ Y).

EXAMPLE 9.15.– (pigeons and rabbits). An example that is frequently given to illustrate constraints is the following.

Determine the X number of pigeons and the Y number of rabbits such that together, they consist of 12 heads and 34 legs.

There is no need for a program, we ask the question:

the answer is:

EXAMPLE 9.16.– (at the restaurant). This program is probably the most famous program that can be found among the examples of Prolog programs in the literature.

A person who must not eat more than a given number of calories during meals wants to come up with the different menus that consist of, say, less than 10 calories. A program that enables us to get all the menus is the following:

By asking the question:

light-meal(e, p,d)

The person will know what menus are possible with 10 or less calories per meal.

EXAMPLE 9.17.– (magic squares). We want to arrange the numbers 1 to 9 in a square in such a way that each row, column, and the two diagonals, all sum to the same constant.

We note:

The program is empty and we ask the question:

(enum(X)

(enum(X) enables us to enumerate the integer values of X that satisfy the constraint):

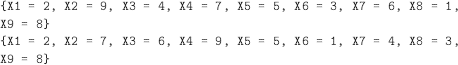
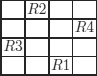
EXAMPLE 9.18.– (the n-queens problem). The well-known n-queens problem consists in placing n queens on an n x n chessboard in such a way that no two queens attack each other. This problem is trivial to program. See also exercise 9.4.

We choose n=4.

The program contains no clause.

In the question, L_i and C_i denote the line and column in which queen i is placed (1 ≤ i ≤ n).. For example, the first solution corresponds to:

% enumerate the solutions

enum(L1) enum(C1) enum(L2) enum(C2) enum(L3) enum(C3) enum(L4)

enum(C4)

% CONSTRAINTS: we begin by the size of the chessboard:

% not on the same line or the same column:

% not on the same diagonals:

% not on the same / diagonals:

% THE SOLUTIONS:

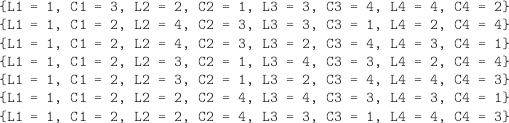
EXERCISE 9.4.– Express the n-queens problem in PL, without using #. Compare with example 9.18.

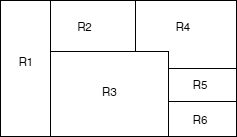
EXAMPLE 9.19.– (map coloring). The problem consists in coloring all the regions of the map below with three distinct colors, in such a way that no two regions with a common border are colored with the same color.

EXAMPLE 9.20.– We want to compute the minimum M of an expression E in a fragment of the plane.

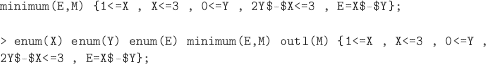
EXAMPLE 9.21.– (non-linear constraints?). Sometimes, they can be handled. The Pythagorean theorem is one such example.

In the constraints, we allowed triangles with collinear sides. To eliminate them, it would suffice to add 1⇐ X, 1⇐ Y in the constraint to obtain the non-degenerate triangles (those marked with (*)) as solutions.

EXAMPLE 9.22.– (syntactic analysis). Grammar rules:

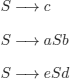
The program:

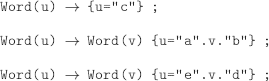
EXAMPLE 9.23.– (scalar product).

where <> denotes a tuple, i.e. a tree whose root is labelled by <>.

EXAMPLE 9.24.– (palindrome on strings). pal(<>) →;

EXAMPLE 9.25.– (reverse on strings). List y is the reverse of list x if their concatenation is a palindrome:

(uses the following property: the length of the list resulting from the concatenation of a list and its reverse is always an even number)

reverse(x, y) → pal(u) {u=x.y, x::m, y::n, m=n};

x::m means: “the length of string x is m”.

EXAMPLE 9.26.– (in a database). (Example given by K. Marriott and J. Stuckey)

A firm wants to reward the faithful employees (defined as those who have stayed at least 10 years in the firm). The part of the database involved with this problem is the following:

Nb: in general, when there are variables we are not interested in (such as Z, U, V, W in the question), we have the possibility of replacing them by _ so as not to choose names for them.

REMARK 9.7.– The substitution {N=0, M=ss(K), K=ss(K)} in the answer to question 2 in the table, corresponds to the generation of an infinite, rational tree (no test for cycles in the unification algorithm, see exercise 4.1).

9.3. Second Order Logic (SOL): a few notions

During the 19th Century and up to the 1910s, in the formal systems used by logicians-mathematicians (Frege, Zermelo, etc.), the usage of higher-order quantifiers (for example, on sets) was common. Formulas and proofs of infinite lengths were also permitted.

It is only during the 1920s (in particular, thanks to Skolem and Hilbert) that FOL started being particularly important.

Using higher-order seems natural because we may wonder “why should we limit the expressive power of the logic we are using?”, i.e. the nature of the objects that can be quantified.

The answer is clear when we take into account the properties of the logic under consideration, other than its expressive power, e.g. existence of denumerable models, semi-decidability, compactness, and completeness, which are useful, in particular, for its automation.

FOL enables us to express many things, in particular, in mathematics, and it has “nice” properties, but some common concepts such as infinite sets, finite sets, well-ordered sets, continuous functions, etc. cannot be expressed in FOL.

SOL (and more generally so-called higher-order logics) enables us to express these concepts and has (have) another characteristic which is that it (they) can greatly reduce the length of proofs of a lower order (for infinitely many formulas).

The notion of expressivity or expressive power corresponds to the models that the formulas of the logic under consideration a to characterize in an exclusive way (meaning some models and they alone).

Characteristic: explicit quantification on predicates and functions.

Advantage: greater expressive power.

Disadvantage: we lose some of the interesting properties of FOL: Löwenheim-Skolem, compactness, and completeness.

We give a few examples that show its usefulness.

EXAMPLE 9.27.– Leibniz’s law (see section 9.1).

EXAMPLE 9.28.– (see also example 9.28).

The induction axiom, intensional version:

The induction axiom, extensional version:

EXAMPLE 9.29.– S is a well-ordered set (meaning that every non-empty subset has a least element):

This property is expressed in weak SOL with successor, which is decidable with a non-elementary complexity, meaning that for any decision algorithm and integer k, there exist formulas of length n such that the decision requires

EXAMPLE 9.30.– (torsion group). This example is often used to show the limits of the expressive power of FOL.

An Abelian group G is a torsion group iff every a G has a finite order, i.e. (e^G denotes the identity in G).

It can also be defined as follows:

denotes the set of subsets of G.)

Or, using an infinitary logic (i.e. that allows formulas of infinite length):

.

EXAMPLE 9.31.– (finite set). We first show that the property of being finite (finiteness) cannot be expressed by a set of wffs of FOL whose models would exclusively be finite sets (obviously of any arbitrary cardinality).

To prove this impossibility, we prove that if such a set of wffs of FOL existed, then it would also admit infinite models.

Assume that Σ, a set of wffs of FOL, has finite models of arbitrary cardinalities.

Consider the formulas of FOL that specify that there exist at least n (distinct) elements (see also theorem 9.1):

where the conjunction contains n(n – 1)/2 disequations.

We define the set .

It is clear that the set is a subset of and is satisfiable (as Σ admits models of all cardinalities and has a model of cardinality at least p).

This property holds for all p, hence, as every finite subset of is satisfiable, by the compactness theorem for FOL (see theorem 5.8), the infinite set also admits a model. This model is infinite (See also the proof of theorem 9.1.).

However, a model of a set of formulas is a model of all its formulas; hence, the infinite model of is an infinite model of Σ. Therefore, Σ cannot exclusively characterize finite sets.

However, it is possible to express finiteness in SOL. According to Dedekind’s definition, a set is finite iff there is no bijection from this set onto one of its proper subsets. In other words, E is finite iff every injective function E → E is onto (this is not the case, e.g. for , with f: → and f(x) → 2 × x).).

We propose three translations.

The first translation:

The second translation (there are only quantifications on predicate variables):

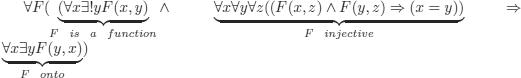
with:

The third translation, “the set whose members have property P is finite” (see also exercise (5.1 n)):

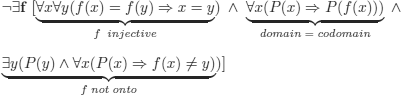
EXAMPLE 9.32.– (infinite set). Dedekind’s definition is sometimes presented for infinite sets.

A set E is infinite iff there exists an injective function with domain E, whose codomain is a proper subset of E:

EXAMPLE 9.33.– (infinite set-2). A set is infinite iff it is the domain of a total, transitive, and irreflexive relation:

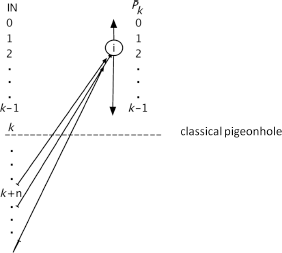
EXAMPLE 9.34.– Sometimes, the pigeonhole principle is formalized by the formula:

where denotes the infinite subsets of

and the following subset of : {0, 1,..., k − 1}

Graphically, this principle can be represented by:

EXAMPLE 9.35.– In natural language, Victor Hugo had all the qualities of a great writer:

X(y): y has quality X.

G(y): y is a great writer.

9.3.1. Syntax and semantics

For the sake of readability, we only present what needs to be added to FOL.

9.3.1.1. Vocabulary

– Predicate variables

– Function variables

(in FOL, we only have variables denoting individuals)

DIGRESSION 9.1.– (variables 3)⁵. In this context too, variables can be replaced by other symbols (syntactic objects) and do not denote quantities that vary (as in mathematics and physics).

9.3.1.2. Syntax

– Atomic formulas can be constructed using predicate and function variables.

– If is a wff, then are also wffs.

9.3.1.3. Semantics

Consider a structure and an interpretation :

– the interpretation assigns to a function in ;

– the interpretation assigns to a relation in ;

– iff for all n_i-ary functions f in ;

– iff there exists an n_i-ary function f in such that

– iff for all n_i-ary relations R in ;

– iff there exists an n_i-ary relation R in , such that .

The compactness theorem (see theorem 5.8) no longer holds in SOL:

THEOREM 9.1.– (non-compactness of SOL). There exists an unsatisfiable set of wffs in SOL only containing finite subsets that are satisfiable.

PROOF.– Given n (n ≥ 2), consider the formula corresponding to the proposition there exists at least n objects:

where the conjunction contains n(n - 1)/2 inequalities.

It is clear from the intended interpretation that each _n is satisfiable in models with universes D of cardinalities at least n (in particular, _n is satisfiable in infinite universes) and unsatisfiable in universes D with card(D) < n.

Consider the set:

S is not finitely satisfiable. Indeed, assume S is finitely satisfiable. Consider a universe D_f such that card(D_f) = n, in which S is satisfied, i.e. that all the formulas in S are satisfied. But there are infinitely many formulas in S that are falsified in D_f: all the formulas for j ≥ 1. Contradiction.

We now consider the set

where _∞ is defined in example 9.33, S_nc is clearly unsatisfiable.

Every finite subset of S_nc is satisfiable, because every {¬_∞, ₂, ₃,..., _n}

(n ) and {_i,... _j} (i, j ) admit finite models (it is not contradictory to admit finite models and not to admit any infinite model).

The set S_nc therefore proves the theorem.

EXAMPLE 9.36.– Specify that a graph is three-colorable, i.e. that we can color all the nodes of the graph with three colors in such a way that two nodes connected by an edge are not colored the same way.

node x has color i

A(x, y): there is an edge between nodes x and y.

EXERCISE 9.5.– (Skolemization and equivalence) (see section 5.5.1.1.).

Prove the equivalence:

where F[x, y] denotes a wff of FOL only containing variables in {x, y} and f a function symbol that does not occur in F[x, y].

EXERCISE 9.6.– Give models of the following formulas:

---

1 A philosopher of logic (W.V.O. Quine) wrote “There is still no entity, no set, nothing without an identity”.

2 Some authors have noted that it can be simplified: .

3 Of course, once the properties of symmetry and transitivity have been proved, they can be used as if they were axioms.

4 Kolmogorov’s probability theory is also monotonic, in the sense that if B is a consequence of A, then prob(A) ≤ prob(B).

5 See also digressions 3.3 and 5.2.