
Finally, you can draw the other branch of the
hyperbola by drawing a circular directrix around
the other focus (of the same radius as the first
one) and repeating the procedure (Figure 11-24).
Eventually, the two branches of the hyperbola
each start to approach a straight line, called the
asymptote. There are two asymptotes, making
sort of an x through the center between the two
branches. As we get farther from the center, the
hyperbola gets closer and closer to these lines.
Their curvature also decreases, so that they
approximate straight lines.
You can see that if the radius of the directrix
changes, you will get a different hyperbola. The
FIGURE 1120: Marking subsequent points on the hyperbola
FIGURE 1122: After marking a series of points
FIGURE 1121: Farther along in drawing the hyperbola (note
bigger “D”)
FIGURE 1123: Sketching in the hyperbola
FIGURE 1124: Drawing the other branch.
Make: Geometry 233
Geometry_Chapter10_v15.indd 233Geometry_Chapter10_v15.indd 233 6/23/2021 9:11:14 AM6/23/2021 9:11:14 AM
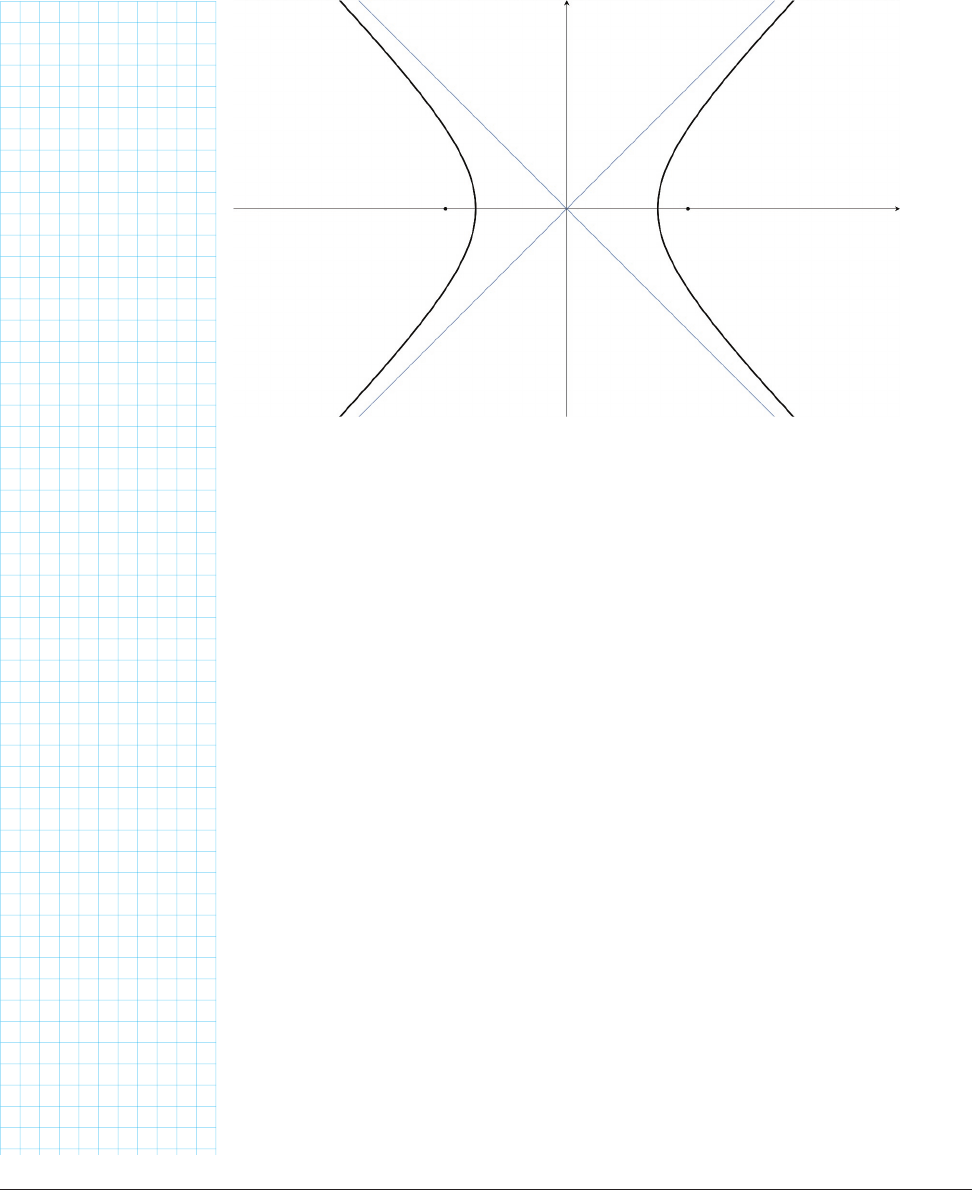
angles at which the asymptotes cross will change, too. Try it!
HYPERBOLA APPLICATIONS
Not every orbit around the sun is a nice, tidy ellipse. Some objects (like
comets) might come in from someplace way out in deep space at such high
speed that they are on a hyperbolic trajectory. They may get close to the sun
(or a planet, in the case of a spacecraft) but their relative velocity is so high
that they will never settle into an elliptical orbit.
Sophisticated telescopes also often combine different types of mirror sur-
faces, like parabolas and hyperbolas, to eliminate distortions. If you were
to make a hyperbolic reflector, light or sound waves generated at the focus
would bounce off at the angles shown by the dotted lines in Figure 11-18.
TYING THE CURVES TOGETHER
Just as we could come up with all the conic sections by cutting a cone (or
two) at steadily increasing angles, so too we can use the methods here to
think of the conics as progressing from ellipse to parabola to hyperbola.
You can think of a hyperbola as an inside-out ellipse, with a parabola as
the intermediate form where one flips to the other. Imagine starting with
an ellipse. If you stay close to one focus and move the other focus away, the
ellipse will get longer and thinner. To do this, it helps to imagine that you are
allowing the ellipse to get larger as it stretches, so that the distance from
FIGURE 1125: Adding the asymptotes.
Make: Geometry 235
234 Chapter 11: Constructing Conics
Geometry_Chapter10_v15.indd 234Geometry_Chapter10_v15.indd 234 6/23/2021 9:11:18 AM6/23/2021 9:11:18 AM
the focus to the edge (that is, the distance a - c) remains constant. When the
other focus is infinitely far away, your curve becomes a parabola. The lines
going from any point on the edge to the distant focus will be parallel, because
converging on a point infinitely far away is the same as not converging at all.
If you think about doing the same with a hyperbola, moving one focus further
and further away while keeping the distance between the near focus and
the curve’s corresponding vertex constant, the other branch of the hyper-
bola will move off to infinity along with the distant focus. This time though,
we’ll choose the focus on the opposite side to be our distant focus. As the
hyperbola stretches and gets bigger, the angle between its asymptotes
gets smaller, and the point where they cross (which is halfway to the distant
focus) also gets further away. When that distance is infinite, the asymptotes
become parallel, and its curvature turns into that of a parabola.
Now, imagine these two parabolas are the same parabola. If you start with
a circle (both foci in the same place), and move one focus out to infinity, it
turns from a circle, to an ellipse, and then into a parabola, which behaves
both as an ellipse with its distant focus infinitely far away in one direction,
and a hyperbola with its distant focus infinitely far away in the other direction.
Because the parabola can be thought of as both, you can think of the distant
focus simultaneously being at both infinities, and able to move away toward
one infinity then come back from the other, like Pacman going out of one side
of the screen and coming back on the other side.
This also amounts to rotating the plane cutting our double cone in Chapter
10, as we progressed from circle, to ellipse, to parabola, and then hyperbola.
There are some tricky ways to mark where the foci are when you are cutting
a plane. If you take a sphere inside the cone that is tangent to the inside of
the cone and the cutting plane, it touches the plane at the focus of the conic
section. These spheres are called Dandelin spheres, and are more than we
want to explore here, but you may enjoy looking them up to learn more.
Make: Geometry 235
Geometry_Chapter10_v15.indd 235Geometry_Chapter10_v15.indd 235 6/23/2021 9:11:18 AM6/23/2021 9:11:18 AM
SUMMARY AND LEARNING MORE
In this chapter, we learned about a different way of constructing conic
sections. Later on, you can use the relationships in this chapter to develop
equations for these three conic sections and explore them that way. You can
find those derivations in a pre-calculus book, or by looking up “derivation of
equation of an ellipse” (or parabola, or hyperbola).
We also learned about some places where ellipses, parabolas, and hyper-
bolas are used in real-life designs. They also come up when explaining
the orbits of planets. In the next chapter, we’ll learn a bit more about how
our planet goes around the sun, and some ways to expand on our ideas in
Chapter 7 about latitude and longitude.
FIGURE 1126: An ellipse.
ANSWERS
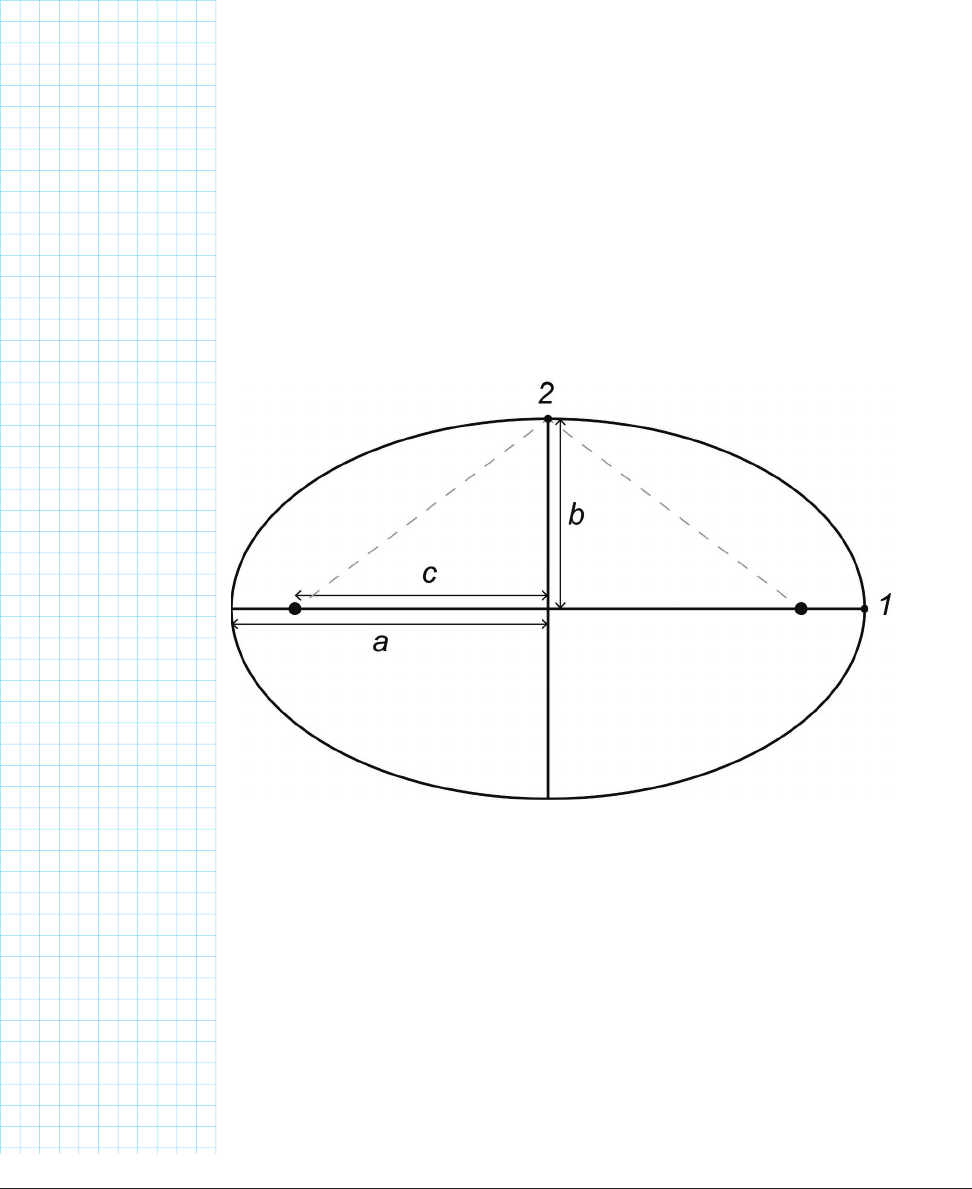
FINDING THE LOCATION OF THE FOCI OF AN ELLIPSE
The easiest way to think about finding the foci is to imagine an ellipse and
to think about a few special cases. If we can prove a relationship for a few
special cases, we can then reason about how to generalize that case to be
sure it will always work. The distance from the center of the ellipse to each
focus is c. The length of the semimajor axis is a and the semiminor, b. This
situation is shown in Figure 11-26.
Make: Geometry 237
236 Chapter 11: Constructing Conics
Geometry_Chapter10_v15.indd 236Geometry_Chapter10_v15.indd 236 6/23/2021 9:11:19 AM6/23/2021 9:11:19 AM

At point 1, the distance from the focus on the left is
a + c.
The distance from the focus on the right is
a - c.
The sum of the two is
a + c + a - c,
or just 2a.Now we know that the sum of the distances from each point on the
ellipse to the two foci is 2a, if that has to be true everywhere.
But that still doesn’t tell us the actual value of c. For that, we need to use
point 2, on the y axis, since our special case ignores anything in the up
and down (in our sketch) direction. At the point labeled “2” in Figure 11-26,
the sum of the distances (dashed lines), by the Pythagorean Theorem, is .
2√
c+b
We also know from what we just figured out with point 1 that this distance
also has to be 2a. So we can set them equal to each other:
2√
c+b
= 2a
Square both sides and divide by 2 to get:
c+b = a, or
c = a-b
If you are used to looking at the Pythagorean Theorem that may bother you,
but in math, the letters a, b, and c are used for many things. Unfortunately,
in this case, it is in a way that fights our Pythagorean instincts from earlier
chapters.
Make: Geometry 237
Geometry_Chapter10_v15.indd 237Geometry_Chapter10_v15.indd 237 6/23/2021 9:11:19 AM6/23/2021 9:11:19 AM
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
