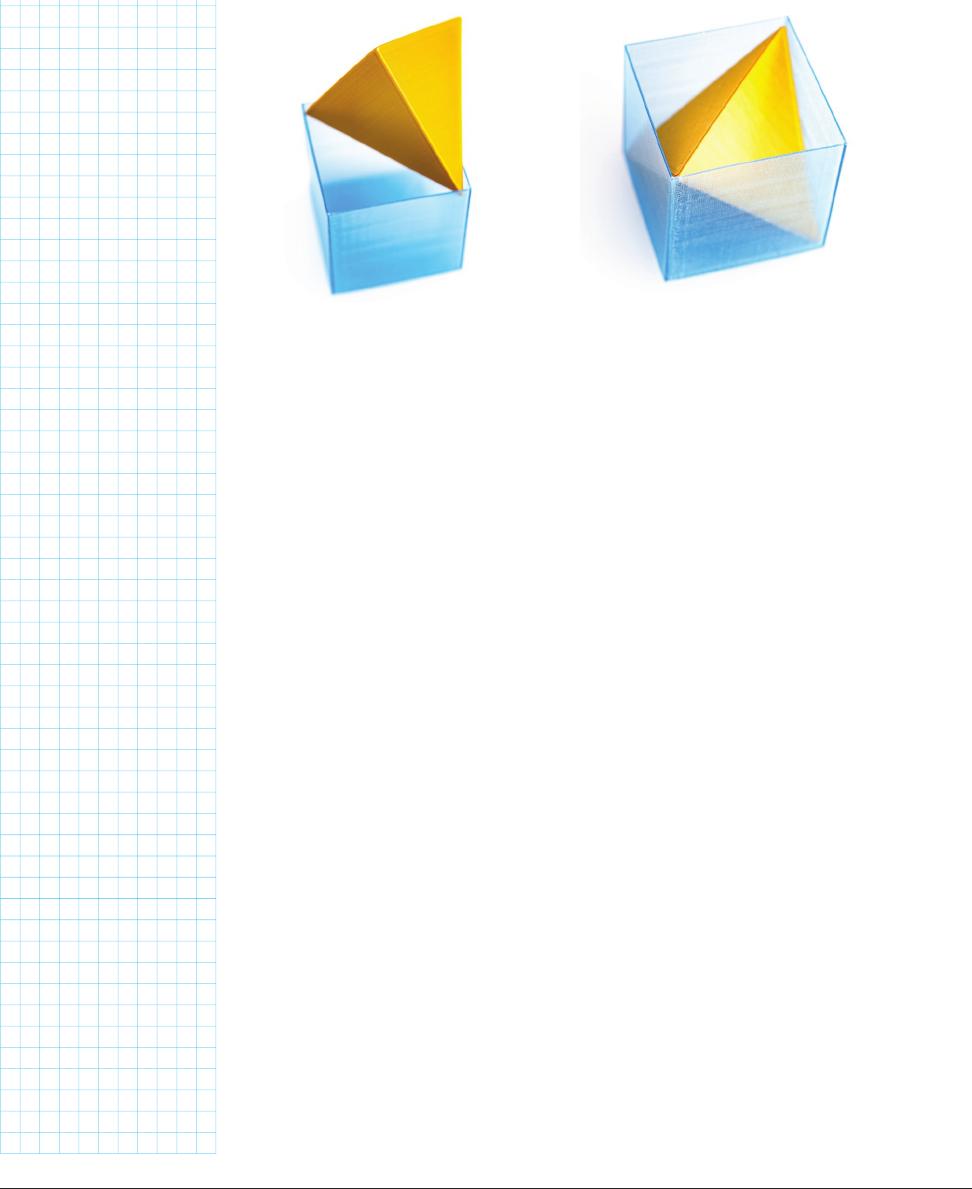
edges are about 40% longer than those of the cube. But if you line up a tetra-
hedron edge with the diagonal of the opening in the cube (Figure 13-35) it will
slide in easily (Figure 13-36). This is a really fun puzzle to just hand someone,
and it is a way to really appreciate the Pythagorean Theorem after you’ve
spent 5 minutes fuming at not being able to get the tetrahedron in the cube.
REULEAUX AND CONSTANT-WIDTH SHAPES IN 3D
Now, let’s check out some other interesting 3D shapes. Back in Chapter 4,
we learned about Reuleaux polygons, which are shapes of constant width.
What happens in the third dimension? Are there 3D shapes of constant
width? It turns out there are several. A technical term for constant-width 3D
shapes is a spheroform. We’ll just call them constant-width shapes here,
since we think that is more descriptive.
REVOLVED REULEAUX POLYGONS
First, think of the Reuleaux polygons we met in Chapter 4. Any of them could
be folded along a line passing through the center and one vertex, and the
sides would line up on top of each other. That line is called an axis of symme-
try, a line that you draw such that a shape is identical (but reflected, like in a
mirror) on either side of it.
Now imagine you take any of the Reuleaux polygons and spin them around that
axis. A mathematician would say revolve it around the axis, and, if we revolve it so
we get a closed 3D figure, the figure is called a surface of revolution.
It turns out that if we revolve any Reuleaux polygon 90 degrees (so that it
fills all the space around its axis) it makes a 3D shape of constant width. Any
cross-section will just be the original polygon, for which this is obviously true.
If it is true for a cross-section, and if the cross-section is the same every-
FIGURE 1336: The tetrahedron in the cube FIGURE 1335: Inserting the tetrahedron in
the cube
Make: Geometry 275
274 Chapter 13: The Geometry Museum
Geometry_Chapter10_v15.indd 274Geometry_Chapter10_v15.indd 274 6/23/2021 9:12:02 AM6/23/2021 9:12:02 AM

where (because you spun the Reuleaux polygon around its axis of symmetry)
then it is true everywhere. The model revolved_reuleaux.scad creates
these models. It has the variables:
• width = 50; //constant width
• reuleaux = 3; // number of sides, odd numbers 3 thru 13
Figure 13-37 shows the figures generated revolved_reuleaux.scad by rotat-
ing the three-sided (triangle), five-sided (pentagon), seven-sided (heptagon)
and nine-sided (nonagon) Reuleaux polygons.
When you roll any of these shapes on a flat surface, the highest point of each
will remain at the same height, just like a sphere. Unlike a sphere though, the
center of mass won’t be equidistant from all of the surfaces, so the shapes
will settle so that their center of mass is at the lowest possible point, rather
than continuing to roll. This is a convenient feature if you need rollers that
you would like to roll freely, but not go careening off every which way.
REULEAUX TETRAHEDRON
Another shape that is very close to a constant width is a Reuleaux tetrahedron.
A Reuleaux tetrahedron is constructed similarly to a Reuleaux triangle, but in 3
dimensions. You make one out of four equal spheres, each with its center placed
where the surfaces of the other three spheres meet. The area where all four
spheres overlap looks like a tetrahedron, but with its edges and faces bowed
outward, like the sides of a Reuleaux polygon. Here is an OpenSCAD model for a
basic Reuleaux tetrahedron made up out of four 50mm spheres.
FIGURE 1337: Left to right: revolved Reuleaux triangle, pentagon, heptagon, nonagon
Make: Geometry 275
Geometry_Chapter10_v15.indd 275Geometry_Chapter10_v15.indd 275 6/23/2021 9:12:02 AM6/23/2021 9:12:02 AM

size = 50;//radius of the spheres
$fs = .2;
$fa = 2;
intersection_for(i = [0:3]) translate(size / sqrt(2) / 2 * [(i
% 2) ? 1 : -1, (i == 1 || i == 2) ? -1 : 1, (i > 1) ? 1 : -1])
sp h e r e(si ze);
Unlike the revolved Reuleaux polygons, a Reuleaux tetrahedron isn’t a true
shape of constant width. It is very close, but when it stands up on one of its
edges, the opposite edge gets slightly higher than it should be if the width
was constant. Thus, the Reuleaux tetrahedron’s largest dimension will be a
little over size mm.
MEISSNER TETRAHEDRONS
A Meissner tetrahedron (named after mathematician Ernst Meissner, who
published it in 1911) is a modified Reuleaux tetrahedron that has three of its
edges rounded-off to make the width constant. Each rounded edge needs
to be opposite an unrounded one. These can be either the three edges that
share a vertex (which will be generated with a value of meissner = 1 in
meissner.scad), or three edges of the same face (meissner = 2). If you set
meissner = 0, it will create a Reuleaux tetrahedron using spheres of radius
= size. You can see all three in Figure 13-38.
size = 50; // radius of the spheres, and also the constant
width
meissner = 1; // Meissner tetrahedron (1 or 2)
// or 0 for Reuleaux tetrahedron
PRINTING THESE MODELS
The various constant-width objects we have been talking about are a little
FIGURE 1338: Reuleaux tetrahedron (blue) and Meissner type 1 (silver) and 2 (red)
Make: Geometry 277
276 Chapter 13: The Geometry Museum
Geometry_Chapter10_v15.indd 276Geometry_Chapter10_v15.indd 276 6/23/2021 9:12:03 AM6/23/2021 9:12:03 AM

tricky to print. Since all of the surfaces are curved, they require some
amount of support when printing. We have been printing ours hollow, and
usually have one of the edges pointed downward to minimize support. When
they are hollow they will be lighter, so you are more likely to get away with
printing them on an edge. Figure 13-39 shows how one of our prints came off
the printer.
Another strategy for printing these shapes would be to cut them in half. This
would give you a large, flat surface that each half can be printed on. After
printing, you would just need to glue the two halves together.
BOUNDING BOX
In Chapter 4 we saw that Reuleaux polyhedra would rotate freely in a bound-
ing polygon of one more side. We didn’t point out that all the polyhedra will
rotate freely in a square (although the higher-number-of-sides ones will
not go as far into the corner of the square). You can try this by extension in a
cube. If you use puzzlebox.scad to create a cube of the same internal dimen-
sion as the constant width of the solids, they will rotate freely (Figure 13-40).
(Be sure to leave enough clearance.)
DUAL POLYHEDRONS
Dual polyhedrons are defined as polyhedra that will fit, one inside the other,
such that the vertices of one are in the exact center of the faces of the other.
This works for just a few polyhedra.
It turns out that an octagon fits inside a cube whose edge is 1/sqrt(2) of the
length of an edge of the cube. (When we 3D print, we also have to allow a
little extra room, of course, so you would make the octagon a millimeter or
FIGURE 1339: Support on a constant-width
solid
FIGURE 1340: Meissner solid rotates freely
in a cube
Make: Geometry 277
Geometry_Chapter10_v15.indd 277Geometry_Chapter10_v15.indd 277 6/23/2021 9:12:05 AM6/23/2021 9:12:05 AM

two smaller.) Figure 13-40 shows this dual. (You can prove to yourself that
this is right by drawing the triangle formed by the line from one vertex of the
octagon to the other.) 1/sqr t(2)is roughly 0.707.
You can make this using the open, hollow cube puzzlebox.scad model with
its default internal side length of 50mm and the edge_platonic_solids.scad
model (introduced in Chapter 3) with
edge = 50 / sqrt(2);
and, as described in Chapter 3, all the functions except the one making an
octahedron commented out.
Placing the octahedron is tricky. It will want to slide around. We put a little bit
of putty on the bottom center of the box to hold that vertex in place.
The octahedron and cube are duals of each other. That means that you
can also make a cube with vertices that touch the center of every face of
an octahedron surrounding it. That, however, would be tricky to 3D print. If
you wanted a significant project to attempt, you could try printing an octa-
FIGURE 1341: The cube-octahedron dual
Make: Geometry 279
278 Chapter 13: The Geometry Museum
Geometry_Chapter10_v15.indd 278Geometry_Chapter10_v15.indd 278 6/23/2021 9:12:06 AM6/23/2021 9:12:06 AM
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
