
We have been talking about angles in degrees to
this point in this book. As we explored in Chapter
5, a degree is a measurement of how big an angle
is. 360° makes a whole circle; a rotation of 180°
points us in the opposite direction (half a circle).
360° was chosen (most likely by the ancient Bab-
ylonians) because it is easy to divide into halves,
thirds, fifths, etc.
Sometimes it is more useful to be able to think
about fractions of a circle in terms of the fraction
along the circle’s perimeter (or circumference)
you have traversed. The unit of that measure-
ment is the radian, which is based solely on values
in nature, like pi. 2π radians take us around a
whole circle. Imagine we have a circle with a
radius = 1 in some units. The circumference of
that circle would be 2πr, where r is the radius.
Since the radius is 1, the circumference is just 2π.
If we had a wedge of the circle with a 45° angle at
the center of the circle, it will have gone through
45/360ths of a circle, which translates to 1/8th of
a circle. If the circumference is 2π, then 2π/8 =
π/4. An angle of 45° is thus the same as an angle
of π/4 radians. 90° is π/2 radians, and 180° is π .
And of course, 360° is 2π radians.
In general, the formula to convert is:
radians = degrees *2 π/360°, or, more simply,
radians = degrees * π /180°.
Or degrees = radians * 180°/ π.
If you use a calculator or computer program to
compute the ratios in this chapter and beyond,
be sure you know whether it is using degrees or
radians. OpenSCAD uses degrees, but most other
computer languages use radians. Calculators that
include trigonometric functions usually let you
switch between degree and radian modes. Goo-
gle’s calculator uses radians.
Just to make things more interesting, sometimes
degrees are shown as decimal degrees, like
34.1028°. Other times, they are shown in degrees,
minutes, and seconds (written like this: 34° 6’
10”, which I would read 34 degrees, 6 minutes, 10
seconds).
To go from degrees-minutes-seconds to frac-
tional degrees, divide minutes by 60 and seconds
by 3600, and add the result to the number of
degrees. Example: 34° 6’ 10” is 34 + 6/60 +
10/3600 = 34.1028°.
To go the other way (from decimal degrees to
minutes and seconds) multiply the decimal part
by 60 to get minutes. For example, if we have
34.1028° and multiply the 0.1 by 60, that’s 6.1667
minutes. If there was a fractional minute, we
would multiply that fraction by 60 again, in this
case, 0.1667 times 60, or 10 seconds.
Degrees, Radians, and Pi
Make: Geometry 113
112 Chapter 6: Pythagoras and a Little Trigonometry
Geometry_Chapter10_v15.indd 112Geometry_Chapter10_v15.indd 112 6/23/2021 9:09:48 AM6/23/2021 9:09:48 AM
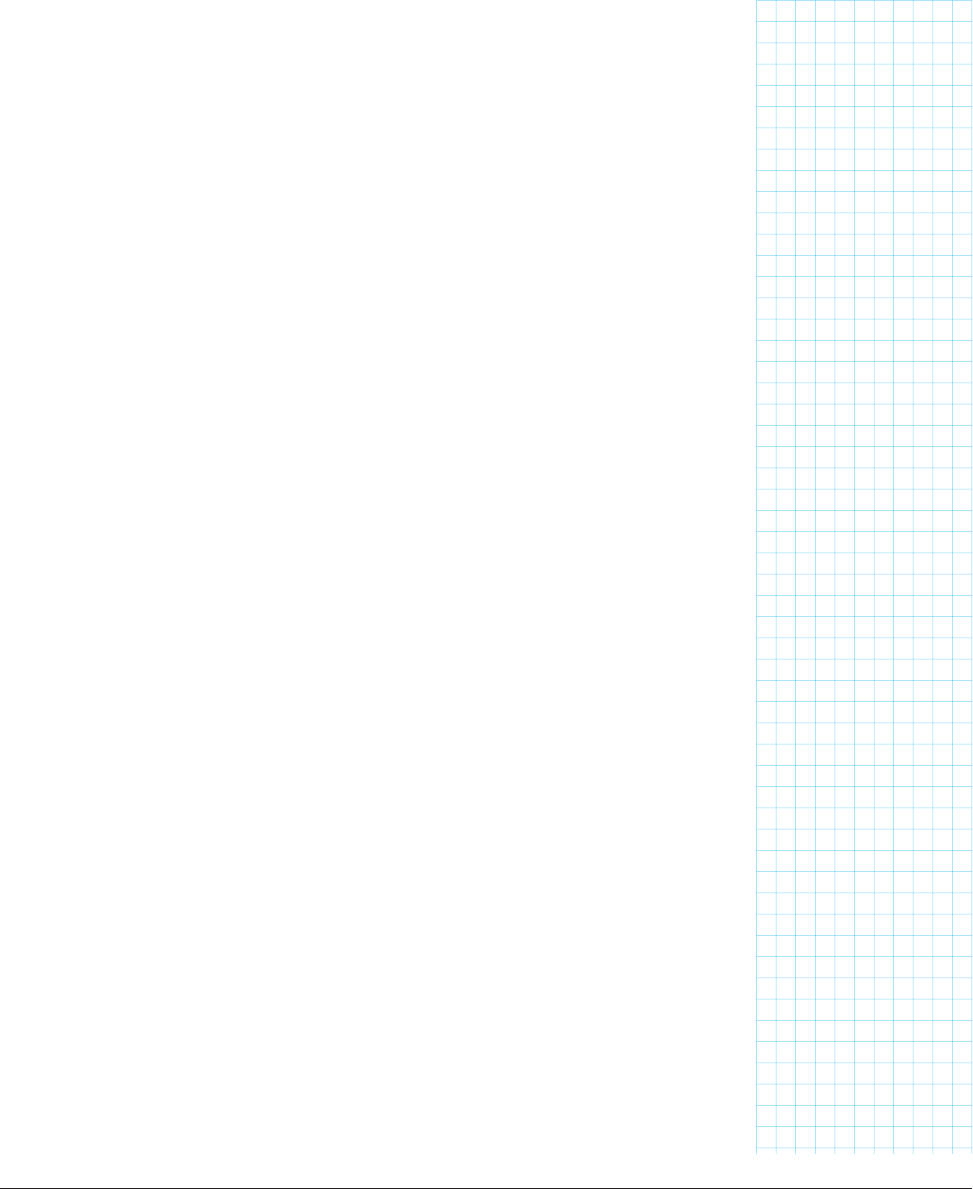
tan(x) = cot(90° - x)
sec(x) = csc(90° - x)
One tricky thing though is that because cosine, sine, and tangent can all go
to zero, secant, cosecant, and cotangent will approach infinity when those
numbers in the denominator go to zero. (A mathematician would say that
dividing by zero is undefined, and these ratios are said to be indeterminate as
they approach infinity.)
FINDING THE LENGTH OF A SIDE
Let’s suppose that we know that an angle of a right triangle is 30°, and the
hypotenuse is 5cm long. What is the length of the opposite side? We can use
a calculator (or estimate with our model) to find out that the sine of 30° is 0.5.
This means that the opposite side is 0.5 times as long as the hypotenuse, or
2.5cm.
sin(30°) = 0.5 = opposite/hypotenuse = opposite/5cm
Do the same thing with cosine to find the adjacent side.
cos(30°) = 0.866 = opposite/hypotenuse = opposite/5cm
Opposite side = 0.866 of the hypotenuse = 0.866 * 5 = 4.33
Note that you can check that you are right because the Pythagorean
Theorem says that the squares of the two sides should equal the square of
the hypotenuse. In our case here, is it true that:
2.5
2
+ 4.33
2
= 5
2
6.25 + 18.75 = 25
25 = 25, so our answer is correct.
CALCULATING WITH SINE AND COSINE
You can test out how well you understood the discussion above by trying to
do some calculations yourself. The answers are at the end of the chapter.
• I have an angle of 45° in a triangle with a hypotenuse 5cm long. What
is the length of the opposite side?
• What is the length of the adjacent side? Why? (Hint: if one angle is
45°, what is the other angle in a right triangle?)
• Check to see that you are right by using the Pythagorean Theorem.
Make: Geometry 113
Geometry_Chapter10_v15.indd 113Geometry_Chapter10_v15.indd 113 6/23/2021 9:09:48 AM6/23/2021 9:09:48 AM

ANGLES NOT BETWEEN 0° AND 90°
What happens if you are trying to take the sine or cosine of an angle larger
than 90° (or negative angles)? The answer is that the definition gets a little
more complicated, but not by a lot. First, let’s remember that in Chapter 2 we
learned about Cartesian coordinate systems, and in Chapter 3, about rotation
and reflection (mirroring, in OpenSCAD).
We’ve printed out a plastic triangle that we can rotate and flip over. Let’s put
x-y coordinate axes behind our triangle. We are interested in the angle at the
vertex of the triangle that is at the center of the coordinate system, which we
will call “A”. We’ve marked it with a small black arrow (Figure 6-14).
To find the sine of that angle, we need the height of the triangle or the side
parallel to the y axis. We’ll call that length y. To get the sine, we would divide y
by the hypotenuse. Similarly, the cosine would be the length in the x direction,
x, divided by the hypotenuse.
Pythagoras would tell us that the hypotenuse would be √
x+y
, so our formu-
las for sine, cosine, and tangent become:
sin(A) = y / √
x+y
cos(A) = x / √
x+y
tan(A) = y / x
So far, except for showing Figure 6-14’s plastic triangle on a coordinate
FIGURE 614: Our original triangle. The small arrow marks the
angle, A.
FIGURE 615: Triangle from 6-14 reflected across the y-axis
Make: Geometry 115
114 Chapter 6: Pythagoras and a Little Trigonometry
Geometry_Chapter10_v15.indd 114Geometry_Chapter10_v15.indd 114 6/23/2021 9:09:49 AM6/23/2021 9:09:49 AM

plane rather than as a triangle with its sides
and angles labeled in isolation, this is the same
situation for finding sine, cosine, and tangent as
we’ve discussed earlier in this chapter.
ANGLES BETWEEN 90 °AND 180°
Now, what would happen if we flipped our tri-
angle over (which a mathematician would call
“reflecting” it across the y axis). Let’s suppose
that now we wanted to know the sine, cosine,
and tangent of the large angle marked by the
arrow in Figure 6-15. This angle is 180°- A, since
together they make a straight line. If we can
figure out what the trigonometric ratios are for
our flipped-over triangle, then maybe we can deduce
what they are for the bigger angle.
Flipping our original triangle over can be thought of as subtracting our angle
A from 180°, because we have to back up angle A degrees from the straight
line, which is 180° from our original starting point for measuring A.
The plastic triangle didn’t change when we mirrored it, did it? So we know its
angle A must be the same (in Figures 6-14 through 6-18 the angle A will stay
the same since it is the same blue plastic triangle). However, the x direction
now points in the other direction, so what was x now becomes -x. The y value,
however, stays the same. The length of the hypotenuse stays the same. Also,
x and (-x) are the same as each other, since a negative multiplied by a nega-
tive is a positive. Given all that, we get:
sin(180° - A) = sin(A) = y / √
x+y
cos(180° - A) = -cos(A) = -x / √
x+y
tan(180° - A) = -tan(A) = y / (-x)
Therefore, to figure out the sine, cosine, and tangent of angles between 90°
and 180°, we subtract the angle from 180° and adjust the signs accordingly.
For example:
sin(120°) = sin(180° - 120°) = sin(60°) = 0.866
cos(150°) = -cos(180° - 150°) = -cos(30°) = -0.866
tan(180°) = -tan(180° - 180°) = tan(0°) = 0
FIGURE 616: Flipping the original triangle in Figure 6-14 over
about the y and then the x axes.
Make: Geometry 115
Geometry_Chapter10_v15.indd 115Geometry_Chapter10_v15.indd 115 6/23/2021 9:09:50 AM6/23/2021 9:09:50 AM
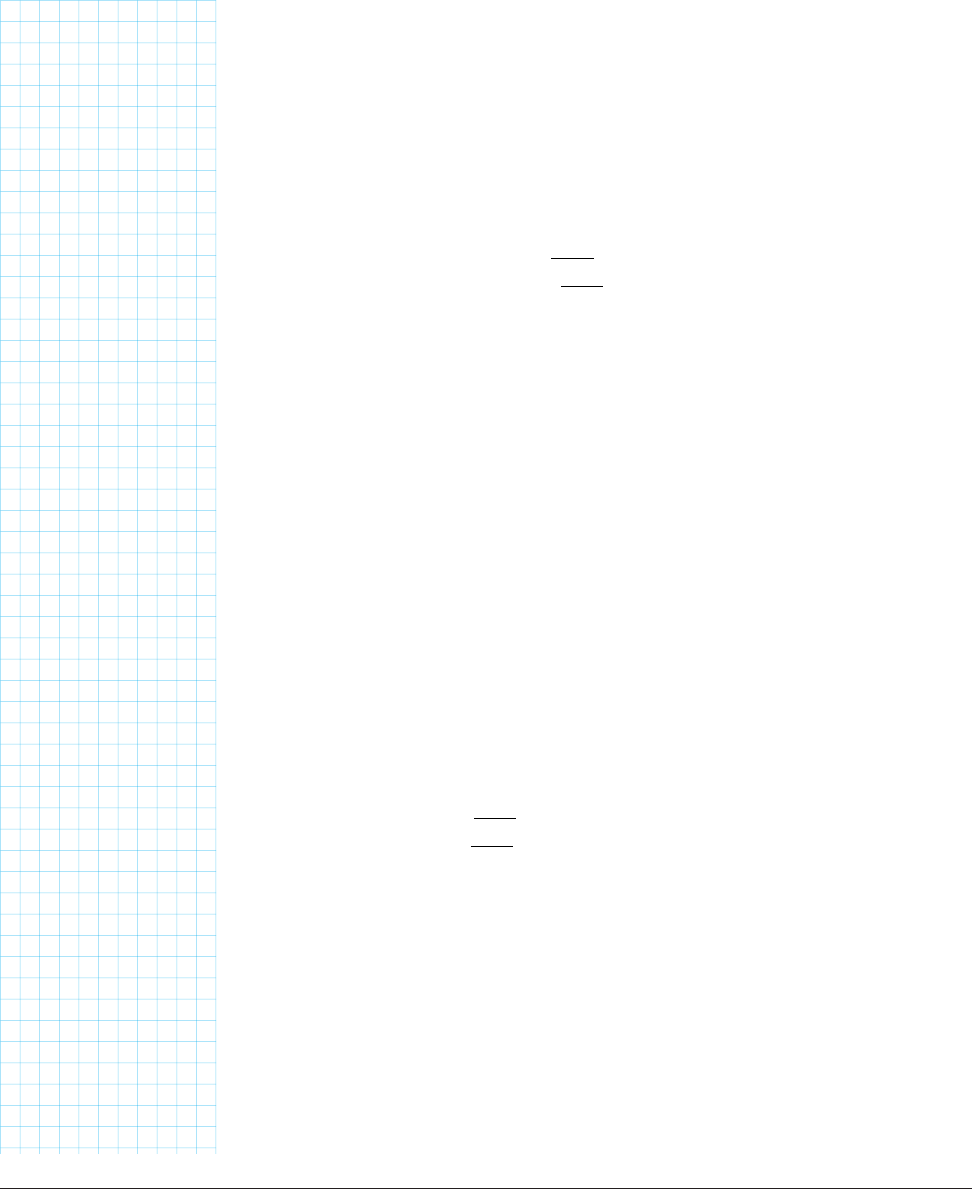
ANGLES BETWEEN 180 °AND 270°
Suppose now we flipped the triangle over again. It’s still the same triangle,
but now both the x and y sides are pointing in the negative direction (Figure
6-16). Now we are going to see if we can find a different relationship between
our original angle and the bigger angle shown in Figure 6-16.
In this case, both the x and y values are negative. We can think of this as
rotating the original triangle to 180° plus A.
sin(180° + A) = -sin(A) = -y / √
x+y
cos(180° + A) = -cos(A) = -x / √
x+y
tan(180° + A) = tan(A) = (-y) / (-x) = y / x
To calculate the sine, cosine, and tangent of the large angle shown in in
Figure 6-16 (an angle between 180° and 270°), we subtract 180° from the
angle, find the sine, cosine, or tangent, and again adjust signs accordingly.
Some examples:
sin(240°) = -sin(240° - 180°) = -sin(60°) = -0.866
cos(180°) = -cos(180° - 180°) = -cos(0°) = -1.000
tan(250°) = tan(250° - 180°) = tan(70°) = 2.748
ANGLES BETWEEN 270° AND 360°
(
OR -90° AND 0°
)
Finally, suppose we went back to the original position of the triangle (where
both x and y were positive) and flipped it over (reflected it) as we can see in
Figure 6-17.
Now x is positive, and y is negative.
sin(360° - A) = -y / √
x+y
cos(360° - A) = x / √
x+y
tan(360° - A) = -y / x
To calculate the sine, cosine, and tangent of the large angle shown in in
Figure 6-17 (an angle between 270° and 360°), we subtract the angle from
360°, find the sine, cosine, or tangent, and again adjust signs accordingly.
Some examples:
sin(300°) = -sin(360° - 300°) = -sin(60°) = -0.866
cos(330°) = cos(360° - 330°) = cos(30°) = 0.866
tan(290°) = tan(360° - 290°) = -tan(70°) = -2.748
Make: Geometry 117
116 Chapter 6: Pythagoras and a Little Trigonometry
Geometry_Chapter10_v15.indd 116Geometry_Chapter10_v15.indd 116 6/23/2021 9:09:50 AM6/23/2021 9:09:50 AM
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
