PLATONIC SOLIDS
Let’s figure out the surface area of the Platonic solids we created in
Chapter 3. To do that, we can look back at the area of inscribed and
circumscribed polygons in Chapter 7 where we compute the area of a
regular polyhedron. Consider printing several of the solids from platonic_
net.scad to follow along with the geometrical reasoning here.
MODIFYING THE MODEL
The model platonic_net.scad creates nets for Platonic solids. It has
these parameters (and default values):
• faces = 4;
• Number of faces
• edge = 10;
• Length of an edge of face, mm
• linewidth = 0;
• Cut/fold line width for 2D export. Set to zero for 3D.
The Platonic solids have faces that are either equilateral triangles,
squares, or regular pentagons. That means we need to find the area of
each of those fundamental shapes, and then add up those areas to get the
surface area of the solid. As we learned in Chapter 3, the apothem is the
distance from the center of a regular polygon that makes a right-angle
intersection with one of its sides.
EQUILATERAL TRIANGLE FACES
Three Platonic solids have equilateral triangle faces: the tetrahedron (4
faces, Figures 9-5 and 9-6), the octahedron (8 faces, back in Figures 9-1
and 9-2), and the icosahedron (20 faces, Figures 9-7 and 9-8). The model
takes as input the apothem, in mm, since that simplifies the math to make
the net. The apothem of an equilateral triangle is just half its height.
To calculate the area of the triangles that make up the faces of the
Platonic solids that have equilateral triangle faces, we can use the
Pythagorean Theorem to find the height (h) of the triangle as a function of
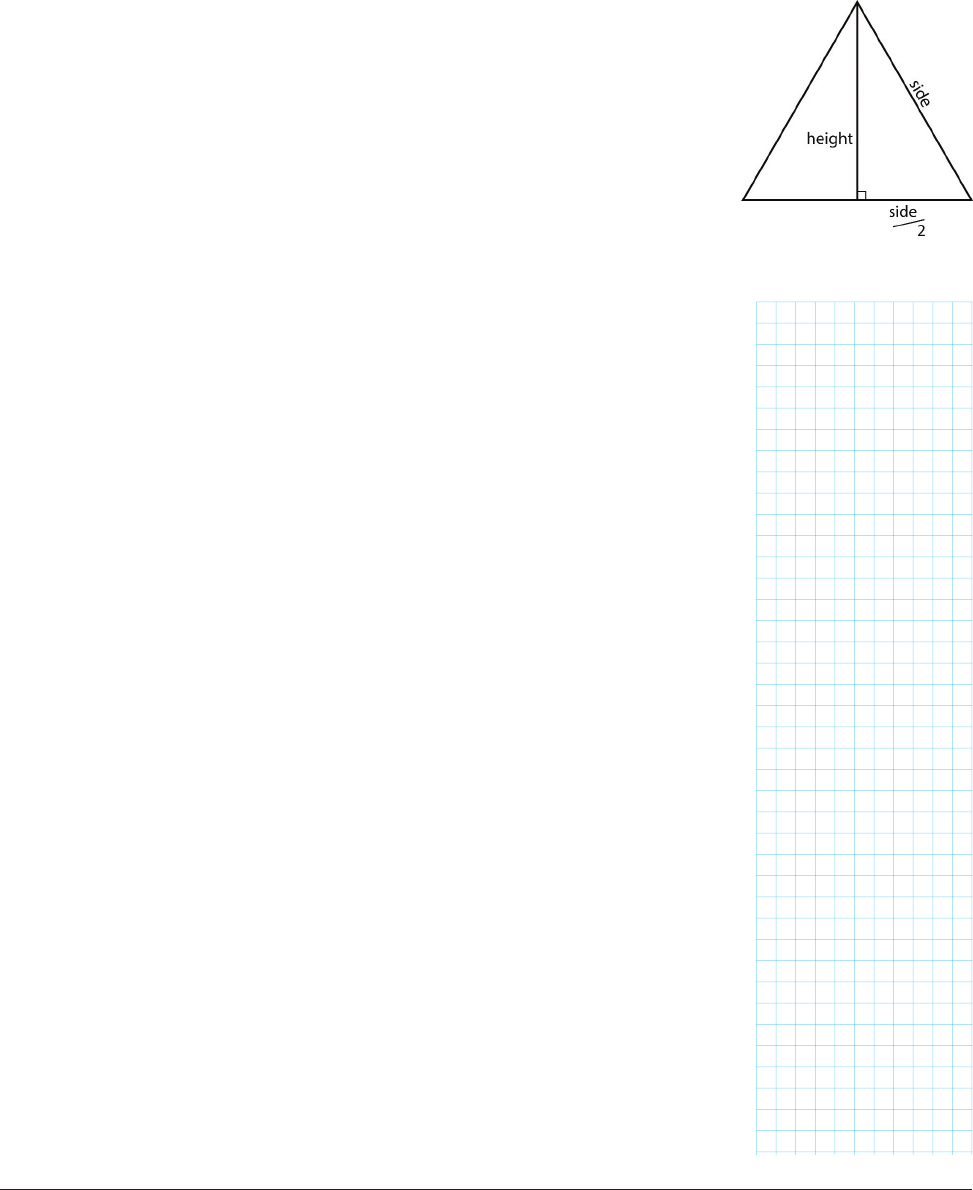
the length of an edge, which we’ll call s, as shown in Figure 9-9.
(s/2)
2
+ (h)
2
=s
2
Which, if we gather up the terms in s, becomes
FIGURE 99: Equilateral triangle
Make: Geometry 181
Geometry_Chapter10_v15.indd 181Geometry_Chapter10_v15.indd 181 6/23/2021 9:10:27 AM6/23/2021 9:10:27 AM

h
2
= 3s
2
/2, or
h = √
3
s /2
The area of each equilateral triangle is 1/2 base times height (twice the
apothem), so we get:
Surface area of each face = (1/2) * s √
3
s /2 = √
3
s
2
/4
You would then multiply this by the number of faces to get the
surface area of the tetrahedron, octahedron or icosahedron. For example,
the icosahedron has 12 sides, so the surface area of the icosahedron is:
Surface area = 12 * 1.7205s
2
= 20.646s
2
SQUARE FACES
The only Platonic solid with square faces is a cube. A cube has 6 faces, and
so we would set faces = 6. Figure 9-10 shows the net open, and Figure 9-11
folded into a cube. The surface area of a cube is just 6 times the area of a
face, which is in turn just the edge length squared.
Surface area of a cube = 6s
PENTAGONAL FACES
A dodecahedron (12 faces) is the only Platonic solid with pentagonal faces.
In Chapter 7 we saw how to compute the area of an n-gon by breaking it up
FIGURE 910: Cube net, open FIGURE 911: Cube net, folded
Make: Geometry 183
182 Chapter 9: Surface Area and Nets
Geometry_Chapter10_v15.indd 182Geometry_Chapter10_v15.indd 182 6/23/2021 9:10:28 AM6/23/2021 9:10:28 AM

into triangles. As we worked out in Chapter 7’s section “Area of Inscribed Polygons”, we can cut the
pentagon into 10 small right triangles, each of which will have a central angle of 36°. The height of this
triangle is the apothem of the polygon (Figure 9-12).
tan(36°) = (s/2) / h, or
h = s/(2 * tan(36°))
Area of the pentagon = (1/2) base * height * 10
= (1/2) s/2 * (s/2)/tan(36°) * 10
= 1.7205 s
2
And so, the surface area of the dodecahedron is just the area of the pentagon * 12. Figure 9-13 shows a
dodecahedron net open (12 faces, pentagonal sides) and Figure 9-14 shows it folded.
FIGURE 912: Anatomy of an inscribed pentagon
FIGURE 913: Dodecahedron net open
FIGURE 914: Dodecahedron net folded
Make: Geometry 183
Geometry_Chapter10_v15.indd 183Geometry_Chapter10_v15.indd 183 6/23/2021 9:10:29 AM6/23/2021 9:10:29 AM
CHECKING SURFACE AREA OF PLATONIC SOLIDS
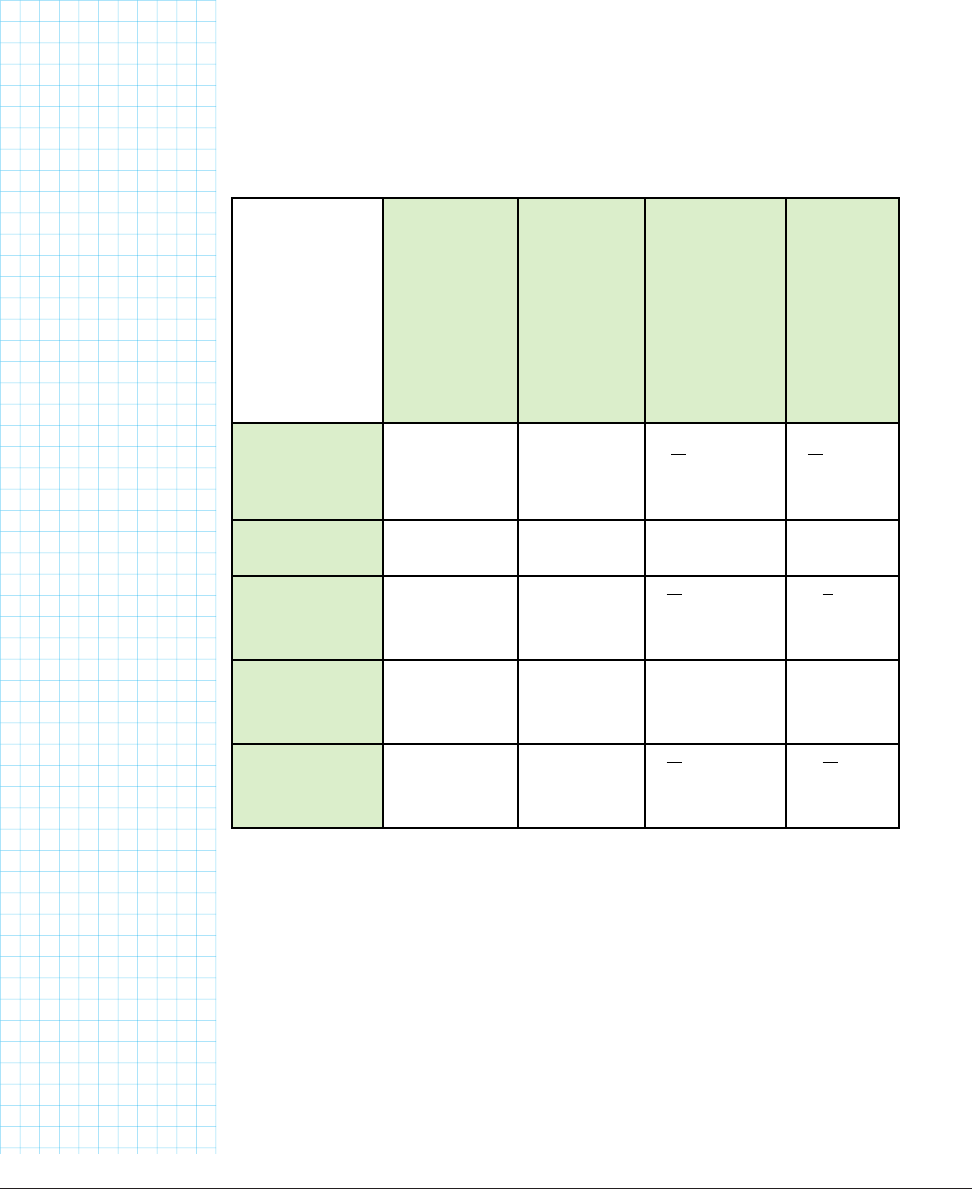
In summary, then, if we want to compute the surface area of a Platonic solid
that we have printed out as a net, we would set the parameter faces to be
the number of faces, and the parameter edge equal to the length of an edge
(side of the face).
Shape of
faces
Number
faces
(faces, in
the model)
Area of face,
as a function
of length
of an edge
(edge in the
model, s
here)
Surface
area of
polyhe-
dron, as
function of
s (edge)
tetrahedron equilateral
triangle
4
√
3
s
2
/4 √
3
s
2
cube square 6 s
2
6s
2
octahedron equilateral
triangle
8 √
3
s
2
/4 2 √
3
s
2
dodecahedron regular
pentagon
12 1.7205 s
2
20.646 s
2
icosahedron equilateral
triangles
20 √
3
s
2
/4 5 √
3
s
2
Print (3D or 2D) several of the Platonic solid nets from platonic_net.scad.
Count up the faces and note the shapes of each face, and see that they match
the entries in this table. Note that these relationships only work if all the
faces are regular polygons identical to each other. Otherwise, the adjacent
faces would have to distort if one face got bigger in any dimension.
Make: Geometry 185
184 Chapter 9: Surface Area and Nets
Geometry_Chapter10_v15.indd 184Geometry_Chapter10_v15.indd 184 6/23/2021 9:10:29 AM6/23/2021 9:10:29 AM
RIGHT PRISMS
A right prism (that is, one whose top and bottom are parallel to and directly
above each other) is a general case of the cube, which we covered under the
Platonic solids. As with a cube, to get the surface area, determine the top
and bottom surface area, and then add that to the rectangles making up the
sides. We will need to calculate the area of the top and bottom by breaking it
up into triangles (as we did for the Platonic solids).
Each rectangle making up a side will have an area of length times height.
There will be n of them, if it is an n-sided prism. The total surface area will
be:
Surface area = 2 * (area of the top) + n * (area of the sides).
MODIFYING THE MODEL
The model pyramid_prism_net.scad prints prisms and pyramids. It has the
following parameters, which are set to defaults as follows:
• r = 20;
• The radius of the base of the prism, in mm
• h = 30;
• The height of the prism (or pyramid), in mm
• sides = 5;
• Number of sides, not including the base
• pyramid = false;
• Set this to false for a prism, true for a pyramid
• star = true;
• If true, it arranges the parts in a star-like arrangement, with
the base in the center.
• linewidth = 0;
• cut/fold line width for 2D export. Set to zero for 3D
• baselayer = 1;
• height of print below (outside) the hinges (in mm)
• printheight = 500;
• total height in mm - set to less than h to have a truncated
pyramid or cone on the inside of the print
• hinge = 0.201;
• thickness of the hinges, in mm. Using a negative value will
leave a gap
Here is an example of the default values, with a pentagonal prism. Figure
Make: Geometry 185
Geometry_Chapter10_v15.indd 185Geometry_Chapter10_v15.indd 185 6/23/2021 9:10:29 AM6/23/2021 9:10:29 AM
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
