8

Clustering and Unsupervised Models for Marketing

This chapter is dedicated to two methods that can be extremely helpful in marketing applications. Unsupervised learning has many interesting applications in contexts where it's necessary to structure the knowledge a business has about customers, in order to optimize promotional campaigns, recommendations, or marketing strategies. This chapter shows how it's possible to exploit a particular kind of clustering to find similarities among sets of customers and products, and how to extract logic rules that describe and synthesize the behavior of customers selecting products from a catalog. Using these rules, marketeers can understand how to optimize their promotions, how to rearrange the position of their products, and what other items could be successfully suggested when a purchase is made.

In particular, the algorithms and topics we're going to analyze are:

• Biclustering based on a spectral biclustering algorithm
• An introduction to market basket analysis with the Apriori algorithm

The first algorithm we're going to analyze is a particular kind of clustering that operates on two levels at the same time. In general, these two levels are correlated by the presence of a medium (for example, customers and products can be correlated by a rating) and the goal of biclustering is to find the regions where such a medium is cohesive (for example, the rating is high or low) by rearranging the structure of both levels (or views).

Biclustering

Biclustering is a family of methods that operate on matrices whose rows and columns represent different features connected with a precise rationale. For example, the rows can represent customers, and the columns products. Each element can indicate a rating or, if zero, the fact that a specific product, p_j, has not been bought/rated by the customer, c_i. As the behavior of the customers can generally be segmented into specific sets, we can assume that A has an underlying checkerboard structure, where the compact regions, called biclusters, represent sub-matrices with peculiar properties.

The nature of such properties depends on the specific context, but the structures share the common feature of being strongly separated from the remaining regions. In our example, the biclusters can be mixed segments containing sets of customers and products that agree on the rating (this concept will be clearer in the practical example), but more generally, the rearrangement of rows and columns of A can highlight highly inter-correlated regions that are not immediately detectable.

In this context, we are going to describe an algorithm developed by Kluger et al. (published in Kluger Y., Basri R., Chang J. T., and Gerstein M., Spectral Biclustering of Microarray Cancer Data: Co-clustering Genes and Conditions, Genome Research, 13, 2003) called spectral biclustering (the term co-clustering is often used as a synonym of biclustering, but it's important to avoid confusion when referring to different algorithms) and initially applied to bioinformatics tasks. The algorithm strongly relies on Singular Value Decomposition (SVD), which will be extensively employed when discussing component analysis and reduction.

The first step, called bistochatization, is a preprocessing iterative phase that entails adjusting the values a_ij so that all column and row sums become equal to a constant common value (normally 1). The name derives from the definition of a stochastic matrix (in other words, all rows or columns total 1) and the result is therefore to have both A and A^T to be stochastic with respect to the columns. The advantage of this step is to reduce the noise caused, for example, by different scales and to unveil regions characterized by large/small variances.

The bistochastic matrix, A_b, is then decomposed using the SVD (further details will be discussed in Chapter 13, Component Analysis and Dimensionality Reduction):

The eigenvectors of and are called, respectively, left and right singular vectors of A_b. The matrix U contains the left singular vectors as columns, while V contains the right singular vectors.

The values on the diagonal of are the singular values, which are the square roots of the eigenvalues of (and . SVD normally sorts the singular values in descending order and the singular vectors are rearranged according to this criterion.

The goal of biclustering is to highlight a checkerboard structure, which can be represented using a particular indicator vector, built with a piecewise constant structure, for example:

It's not difficult to understand that such a vector is internally split into homogenous components that can represent (in one-dimensional projection) the biclusters we're looking for. The algorithm proceeds by ranking the singular vectors by analyzing their similarity with (whose structure also depends on dimensions of the matrix A). If the desired number of biclusters is denoted with k, a projection matrix P_k is built using the top k singular vectors. The dataset (represented by A) is then projected onto the sub-space spanned by the columns of P_k. At this point, the checkerboard structure is easily discoverable because, in the new sub-space, the biclusters are made up of points close to one another (in other words, they make up dense regions separated by empty ones).

To better clarify this concept, let's consider the first column, c₁, of P_k. By definition, it contains the singular vector with the highest similarity to . After performing the projection, the original first component is rotated so as to overlap c₁. The process is repeated for all the remaining components. In this new reference system, the original points will therefore be associated by coordinates (features) indicating their similarity with respect to a particular bicluster.

The algorithm finishes by applying K-Means to find the labelling for the k clusters. This operation is performed in consideration of both rows and columns, yielding two label vectors, and . It's easy to prove (but we are skipping this step) that the rearranged matrix with the checkerboard structure is obtained by applying the outer product to sorted vectors, and (which are simply the original vectors whose components have been sorted in ascending order):

We can now show a complete Python example based on a marketing dataset containing several purchase mixes.

Example of Spectral Biclustering with Scikit-Learn

In this and the following example, we are going to work with a synthetic transaction dataset containing 100 purchase mixes in the form{p_i, p_j, …,p_k} with 100 products and . The dataset is enriched with a rating matrix , where 0 indicates the absence of a rating and a value is considered an explicit rating. The goal of this example is to use biclustering to find the underlying checkerboard structure.

Let's start creating the dataset:

import numpy as np
nb_users = 100
nb_products = 100
items = [i for i in range(nb_products)]
transactions = []
ratings = np.zeros(shape=(nb_users, nb_products),
                       dtype=np.int)
for i in range(nb_users):
        n_items = np.random.randint(2, 60)
        transaction = tuple(
            np.random.choice(items,
                             replace=False,
                            size=n_items))
        transactions.append(
            list(map(lambda x: "P{}".format(x + 1),
                     transaction)))
        for t in transaction:
            rating = np.random.randint(1, 11)
            ratings[i, t] = rating

A heatmap of the initial rating matrix is shown in the following diagram:

Heatmap of the rating matrix. Black cells indicate the absence of a rating

The matrix is sparse (when the dimensionality is larger, I suggest employing SciPy sparse matrices to save space), but every user has rated at least 2 products, with an approximate average of 30. In this example, we are interested in discovering the segments of user/product mixes characterized by the same rating. As each rating is in the range (1, 10), also considering the non-rating segment, there are 10 different possible biclusters with immediate semantics.

At this point, we can train the model using n_best=5 to indicate that we want to project the dataset onto the top five singular vectors and svd_solver="arpack", which is a very accurate SVD algorithm suitable for small/medium-sized matrices:

from sklearn.cluster.bicluster import SpectralBiclustering
sbc = SpectralBiclustering(n_clusters=10, n_best=5,
                           svd_method="arpack",
                           n_jobs=-1,
                           random_state=1000)
sbc.fit(ratings)
rc = np.outer(np.sort(sbc.row_labels_) + 1, 
                  np.sort(sbc.column_labels_) + 1)

As explained in the theoretical part, the final matrix is computed using the outer product of the sorted row and column indices.

Before showing the final result, we want to demonstrate how to find the mixes. Let's suppose that we are interested in determining the group of users {u_i, u_j, …, u_t} that rated a group of eight products {p_i, p_j, …, p_t} in order to send a periodical newsletter containing tailored recommendations. This operation can be easily achieved by selecting all the rows and columns associated with the biclusters with an index of 8 (remember that 0 corresponds to the absence of a rating):

import numpy as np
print("Users: {}".format(
        np.where(sbc.rows_[8, :] == True)))
print("Product: {}".format(
        np.where(sbc.columns_[8, :] == True)))

The raw output of the previous snippet (with a random seed set to 1,000) is as follows:

Users: (array([30, 35, 40, 54, 61, 86, 87, 91, 94], dtype=int64),)
Product: (array([49, 68, 93], dtype=int64),)

Therefore, we can check the family of the products {49, 68, 93}, select some similar items, and send them in the suggestion part of the newsletter to the users {30, 35, 40, 54, 61, 86, 87, 91, 94}. We can now show the final matrix with a checkerboard structure:

Heatmap of the rating matrix after biclustering

As it's possible to see, the matrix is split into homogeneous regions corresponding to the same rating. In practical applications, it can be helpful to select, for example, the mix corresponding to the ratings to recommend similar products, and the mix {u_i, r_ij < 6} to ask for feedback regarding their negative ratings. I'll leave these two cases as exercises for the reader.

After this discussion about biclustering, let's now analyze a simple but effective way to perform market basket analysis and find association rules given a set of transactions.

Introduction to Market Basket Analysis with the Apriori Algorithm

In the previous example, we analyzed the ratings provided by different customers in order to perform mixed segmentation. However, sometimes, a company only has complete knowledge about the set of products bought by its customers. More formally, given a set P = {p₁, p₂, …, p_n} of products, a transaction, T_i, is a subset of P:

A collection of transactions (often called a database) is a set of subsets, T_i:

The main goal of market basket analysis is to mine all existing association rules that can be expressed in the generic form:

To avoid confusion, the previous expression means that, given a transaction containing a set of items, the probability of finding the item p_t is greater than a discriminant threshold, (for example, 0.75). The value of this process is straightforward because a company can optimize its offers based on the evidence provided by the actual transactions. For example, a retailer can discover that customers buying a specific smartphone model also buy a case and, consequently, can create ad hoc offers and attract more customers.

Unfortunately, the number of all possible transactions, N_T, is equal to the cardinality of the power set of P. If we limit ourselves to the presence/absence of an item, N_T = 2ⁿ, this can easily lead to intractable problems (for example, if there are just 1,000 products, N_T is a number with more than 300 digits). For this reason, Agrawal and Srikant (in Agrawal R., Srikant R., Fast Algorithms for Mining Association Rules, Proceedings of the 20th VLDB Conference, 1994) proposed an algorithm, called Apriori, whose goal is to allow the mining of relatively large datasets in a reasonable time (considering that the paper was published in 1994, the reader can easily imagine how simple this process is nowadays).

Given a discrete probability distribution over a set D the region where is called support of the distribution. Given a generic rule, , its probabilistic confidence is the ratio between the support of P(A, B) and the support of P(A). We are going to employ and further analyze these concepts later, when defining the strategy adopted by this algorithm.

The main assumption of the Apriori algorithm is that only a small portion of the probability space with (in other words, the support of ). In particular, when working with large datasets, the number of valid combinations is a very small fraction of the power set, therefore it doesn't make sense trying to model the full joint probability distribution.

As we are working with discrete variables, the support of an item p_i or of an item set {p_i, p_j, …, p_k} can be computed with a frequency count. Given the maximum number of items in a transaction, Apriori starts computing the support of all products S(p_i) and removing all the items with (with ). Indeed, we are not very interested in products that are seldom sold. Therefore, the first selection can be considered as a zoom into the region where all the most common transactions are located. Apriori proceeds by analyzing all couples, triplets, and so on and applying the same filter. The results of each pass are item sets that can be split into disjointed subsets to make up the association rules. For example:

The rules have the standard format of logical implications, , where A is the antecedent and A is the consequent. Of course, it must be clear that, while in propositional logic, the previous expression is deterministic, in market basket analysis, it's always probabilistic. Therefore, it's helpful to introduce a measure to evaluate the validity of each rule. Continuing with a logical approach, we can extend the concept of modus ponens, which states that:

In a probabilistic scenario, we are interested in quantifying how frequently the consequent is true when the whole rule is true. In other words, given the support of the original item set (before the split) S(I) and, assuming that I has been split into {A, B}, a common measure is the confidence of a rule C(I) (often represented as an item set):

This value can always be computed as the threshold ; therefore, neither the numerator nor the denominator can be null. If the rule always applies, S(A) = S(I) and C(I) = 1, while all other values in the range (0, 1) indicate increasingly infrequent rules. As the confidence is immediate to compute (all the data is already available during the steps), Apriori enables the setting of another threshold, excluding all those rules where (with ).

The algorithm is extremely simple and effective, but there are some evident drawbacks. The most problematic one is the necessity of setting large thresholds when the datasets are very large. In fact, most modern B2C companies have millions of users who are interested in small portions of items. The application of a vanilla Apriori algorithm might exclude a large number of custom rules that are valid for specific customers. Therefore, in all these cases, it's preferable to perform an initial segmentation of the customers and then apply Apriori to each subset of transactions. Another feasible strategy is based on a process of transaction generalization, which consists of transforming a transaction, T_i, in a particular feature vector containing dummy products that also represent large subsets of items:

The elements f_i are not real products, but rather classes that contain similar items. This method has the advantage of allowing fast recommendations based on the joint support of the rules or, in a more advanced scenario, on the joint subset of the last k rules activated by the transactions (in other words, the last product bought by the customer has higher priority than the ones present in non-recent transactions).

Example of Apriori in Python

We can now employ the efficient-apriori Python library (available on https://pypi.org/project/efficient-apriori/ and installable by using the pip install -U efficient-apriori command) to mine the transaction dataset created in the previous example and detect all the rules with a maximum length equal to 3. As the dataset is quite small, we are going to set min_support = 0.15, but we want to be sure to find reliable rules, hence the minimum confidence is set equal to 0.75. We have also set the parameter verbosity=1 to show the messages throughout the learning process:

from efficient_apriori import apriori
_, rules = apriori(transactions,
                   min_support=0.15,
                   min_confidence=0.75,
                   max_length=3,
                   verbosity=1)

The output of the previous snippet is:

Generating itemsets.
 Counting itemsets of length 1.
  Found 100 candidate itemsets of length 1.
  Found 100 large itemsets of length 1.
 Counting itemsets of length 2.
  Found 4950 candidate itemsets of length 2.
  Found 1156 large itemsets of length 2.
 Counting itemsets of length 3.
  Found 6774 candidate itemsets of length 3.
  Found 9 large itemsets of length 3.
Itemset generation terminated.
Generating rules from itemsets.
 Generating rules of size 2.
 Generating rules of size 3.
Rule generation terminated.

The reader can immediately identify the steps described in the theoretical part. In particular, the algorithm proceeds by defining the item sets (starting from a length of 1 and ending with the desired limit) and filtering out the elements with support below the minimum threshold (0.15). Let's now check the rules that have been found:

print("No. rules: {}".format(len(rules)))
for r in rules:
print(r)

The output is as follows:

No. rules: 22
{P31, P79} -> {P100} (conf: 0.789, supp: 0.150, lift: 2.024, conv: 2.897)
{P100, P79} -> {P31} (conf: 0.789, supp: 0.150, lift: 2.134, conv: 2.992)
{P66, P68} -> {P100} (conf: 0.789, supp: 0.150, lift: 2.024, conv: 2.897)
{P100, P68} -> {P66} (conf: 0.750, supp: 0.150, lift: 2.419, conv: 2.760)
{P11, P97} -> {P55} (conf: 0.750, supp: 0.150, lift: 2.143, conv: 2.600)
{P11, P55} -> {P97} (conf: 0.789, supp: 0.150, lift: 2.024, conv: 2.897)
{P21, P7} -> {P15} (conf: 0.789, supp: 0.150, lift: 2.134, conv: 2.992)
{P15, P7} -> {P21} (conf: 0.750, supp: 0.150, lift: 2.206, conv: 2.640)
{P15, P21} -> {P7} (conf: 0.750, supp: 0.150, lift: 2.027, conv: 2.520)
{P46, P83} -> {P15} (conf: 0.789, supp: 0.150, lift: 2.134, conv: 2.992)
{P15, P83} -> {P46} (conf: 0.750, supp: 0.150, lift: 1.974, conv: 2.480)
{P15, P46} -> {P83} (conf: 0.789, supp: 0.150, lift: 2.322, conv: 3.135)
{P59, P65} -> {P15} (conf: 0.750, supp: 0.150, lift: 2.027, conv: 2.520)
{P15, P65} -> {P59} (conf: 0.789, supp: 0.150, lift: 2.078, conv: 2.945)
{P55, P68} -> {P36} (conf: 0.750, supp: 0.150, lift: 2.419, conv: 2.760)
{P36, P68} -> {P55} (conf: 0.789, supp: 0.150, lift: 2.256, conv: 3.087)
{P36, P55} -> {P68} (conf: 0.789, supp: 0.150, lift: 2.024, conv: 2.897)
{P4, P97} -> {P55} (conf: 0.842, supp: 0.160, lift: 2.406, conv: 4.117)
{P4, P55} -> {P97} (conf: 0.800, supp: 0.160, lift: 2.051, conv: 3.050)
{P56, P79} -> {P47} (conf: 0.762, supp: 0.160, lift: 2.116, conv: 2.688)
{P47, P79} -> {P56} (conf: 0.842, supp: 0.160, lift: 2.216, conv: 3.927)
{P47, P56} -> {P79} (conf: 0.842, supp: 0.160, lift: 2.477, conv: 4.180)

Hence, Apriori found 22 rules of length 2. The confidence ranges between (0.75, 0.84), while the support is always close to 0.15 (this is due to the cardinality of the dataset). The high confidence is helpful in excluding all the rules with a low probability. However, high confidence is not always enough to understand whether the rule is based on a large or small number of transactions.

As it's possible to see, after the support, the algorithm outputs a value called lift, which is defined as:

This index is proportional to the ratio between the joint probability of the rule (in other words, ) and the product of the probabilities of the antecedent and consequent (in other words, ). The ratio ; therefore, taking into account that and , the lift will always be greater than or equal to the confidence. Moreover, as C(I) = L(I)S(B), for a fixed confidence, the smaller S(B) is, the larger L(I) must be. Ideally, we'd like to have a lift equal to 1, indicating that all transactions contain the element(s) in B. In real cases, this is almost impossible; hence, the lift is generally greater than 1.

For example, for a rule with C(I)= 0.75 and L(I) = 2, the support of the consequent is 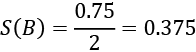. In our example, all consequents contain a single value (which is the standard choice for market basket analysis).

Therefore, it's extremely easy to associate the lift with the probability of finding the product in a random transaction. In most real cases, a lift in the range (1.5, 2.5) is quite reasonable, while rules with, for example, a lift corresponding to S(B) < 0.05 cannot be considered solid enough to be trusted even if the confidence is large.

On the other hand, a support S(B) close to 1 is associated with a trivial rule, because most of the transactions contain that product (for example, a convenience store could have accidently included the shopping bags in the transactions, and therefore their lift is often close to 1, but it doesn't make sense to recommend them). The optimal threshold for lift depends on the context and, contrary to confidence, it is better to define an interval because low and high values are both negative indicators for all affected rules.

For example, a B2C company could set up two sections of their newsletter. In the first one, they could include products with a large confidence (C(I) > 0.8) and a lift close to 2 (which normally corresponds to ). These recommendations are confirmed by a large number of customers. Therefore, there's a high conversion probability. Instead, in the second section, it's possible to include products with a smaller S(B) (in other words, a larger lift) that have been selected by a niche group of customers.

Summary

In this chapter, we introduced two algorithms that are very helpful in marketing scenarios. Biclustering is a method for performing clustering on a matrix dataset with two different views correlated by a medium factor. The model facilitates the discovery of the checkerboard structure of such a dataset and can be employed whenever it's helpful to discover segments of elements (for example, customers or products) that share the same medium factor. A classic application is the creation of recommender systems that can immediately identify the similarities existing between a group of customers and products and help marketeers to provide suggestions with a high conversion likelihood.

Apriori is an efficient solution for performing market basket analysis on large transaction datasets. It enables discovery of the most important association rules existing in the dataset so as to plan optimal marketing strategies. Classical applications are product segmentation, promotion planning, and, in some cases, logistic planning, too. In fact, the algorithm can be applied to any kind of transactional dataset and, whenever it's helpful, it's also possible to rearrange the position of the items (generically speaking) so as to minimize the time necessary to complete the most important transactions.

In the next chapter, Chapter 10, Introduction to Time-Series Analysis, we're going to introduce the reader to the concepts of generalized linear models and time series, focusing attention on the main techniques and models that can be employed to implement complex scenarios.

Further reading

• Aggarwal C. C., Hinneburg A., Keim D. A., On the Surprising Behavior of Distance Metrics in High Dimensional Space, ICDT, 2001
• Arthur D., Vassilvitskii S., The Advantages of Careful Seeding, k-means++. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2006
• Pedrycz W., Gomide F., An Introduction to Fuzzy Sets, The MIT Press, 1998
• Shi J., Malik J., Normalized Cuts and Image Segmentation, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 22, 08, 2000
• Gelfand I. M., Glagoleva E. G., Shnol E. E., Functions and Graphs, Vol. 2, The MIT Press, 1969
• Biyikoglu T., Leydold J., Stadler P. F., Laplacian Eigenvectors of Graphs, Springer, 2007
• Ester M., Kriegel H. P., Sander J., Xu X., A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, AAAI Press, pp. 226-231, 1996
• Kluger Y., Basri R., Chang J. T., Gerstein M., Spectral Biclustering of Microarray Cancer Data: Co-clustering Genes and Conditions, Genome Research, 13, 2003
• Huang, S., Wang, H., Li, D., Yang, Y., Li, T., Spectral Co-clustering Ensemble. Knowledge-Based Systems, 84, 46-55, 2015
• Bichot, C., Co-clustering Documents and Words by Minimizing the Normalized Cut Objective Function. Journal of Mathematical Modelling and Algorithms, 9(2), 131-147, 2010
• Agrawal R., Srikant R., Fast Algorithms for Mining Association Rules, Proceedings of the 20th VLDB Conference, 1994
• Li, Y., The application of the apriori algorithm in the area of association rules. Proceedings of the SPIE, 8878, 88784H-88784H-5, 2013
• Bonaccorso G., Hands-On Unsupervised Learning with Python, Packt Publishing, 2019