2

Loss Functions and Regularization

Loss functions are proxies that allow us to measure the error made by a machine learning model. They define the very structure of the problem to solve, and prepare the algorithm for an optimization step aimed at maximizing or minimizing the loss function. Through this process, we make sure that all our parameters are chosen in order to reduce the error as much as possible. In this chapter, we're going to discuss the fundamental loss functions and their properties. I've also included a dedicated section about the concept of regularization; regularized models are more resilient to overfitting, and can achieve results beyond the limits of a simple loss function.

In particular, we'll discuss:

• Defining loss and cost functions
• Examples of cost functions, including mean squared error and the Huber and hinge cost functions
• Regularization
• Examples of regularization, including Ridge, Lasso, ElasticNet, and early stopping techniques

We'll begin with some definitions related to loss and cost functions.

Defining loss and cost functions

Many machine learning problems can be expressed throughout a proxy function that measures the training error. The obvious implicit assumption is that, by reducing both training and validation errors, the accuracy increases, and the algorithm reaches its objective.

If we consider a supervised scenario (many considerations hold also for semi-supervised ones), with finite datasets X and Y:

We can define the generic loss function for a single data point as:

J is a function of the whole parameter set and must be proportional to the error between the true label and the predicted label.

However, for now, it's useful to consider a loss function as an intermediary between our training process and a pure mathematical optimization. The missing link is the complete data. As already discussed, X is drawn from p_data, so it should represent the true distribution. Therefore, when we minimize the loss function, we're considering a potential subset of points, and never the whole real dataset.

In many cases, this isn't a limitation. If the bias is null and the variance is small enough, the resulting model will show a good generalization ability, with high training and validation accuracy; however, considering the data generating process, it's useful to introduce another measure called expected risk:

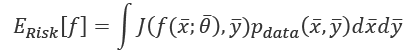
This value can be interpreted as an average of the loss function over all possible samples drawn from p_data. However, as p_data is generally continuous, it's necessary to consider an expected value and integrate over all possible couples, which is often an intractable problem. The minimization of the expected risk implies the maximization of global accuracy, which, in turn, corresponds to the optimal outcome.

On the other hand, in real-world scenarios we work with a finite number of training samples. Since that's the case, it's preferable to define a cost function, which is often called a loss function as well, and is not to be confused with the log-likelihood:

This is the actual function that we're going to minimize. Divided by the number of samples (a factor that doesn't have any impact) it's also called empirical risk. It's called that because it's an approximation, based on a finite sample X, of the expected risk. In other words, we want to find a set of parameters so that:

When the cost function has more than two parameters, it's very difficult and perhaps even impossible to understand its internal structure. However, we can analyze some potential conditions using a bidimensional diagram:

Different kinds of points in a bidimensional scenario

The different situations we can observe are:

• The starting point, where the cost function is usually very high due to the error.
• Local minima, where the gradient is null and the second derivative is positive. They're candidates for the optimal parameter set, but unfortunately, if the concavity isn't too deep, an inertial movement or noise can easily move the point away.
• Ridges (or local maxima), where the gradient is null, and the second derivative is negative. They are unstable points, because even minimal perturbation allows escape toward lower-cost areas.
• Plateaus, or regions where the surface is almost flat and the gradient is close to zero. The only way to escape a plateau is to keep some residual kinetic energy—we're going to discuss this concept when talking about neural optimization algorithms in Chapter 18, Optimizing Neural Networks.
• Global minimum, the point we want to reach to optimize the cost function.

Even if local minima are likely when the model has a small number of parameters, they become very unlikely when the model has a large number of parameters. In fact, an n-dimensional point is a local minimum for a convex function (and here, we're assuming L to be convex) only if:

The second condition imposes a positive definite Hessian matrix—equivalently, all principal minors made with the first n rows and n columns must be positive—therefore all its eigenvalues must be positive. This probability decreases with the number of parameters ( is an n × n square matrix and has n eigenvalues), and becomes close to zero in deep learning models where the number of weights can be in the order of millions, or even more. The reader interested in a complete mathematical proof can read Dube S., High Dimensional Spaces, Deep Learning and Adversarial Examples, arXiv:1801.00634 [cs.CV].

As a consequence, a more common condition to consider is instead the presence of saddle points, where the eigenvalues have different signs and the orthogonal directional derivatives are null, even if the points are neither local maxima nor local minima. Consider, for example, the following plot:

Saddle point in a three-dimensional scenario

The surface is very similar in shape to a horse saddle, and if we project the point on an orthogonal plane, XZ is a minimum, while on another plane (YZ) it is a maximum. It's straightforward that saddle points are quite dangerous, because many simpler optimization algorithms can slow down and even stop, losing the ability to find the right direction. In Chapter 18, Optimizing Neural Networks, we're going to discuss some methods that are able to mitigate this kind of problem, allowing deep models to converge.

Examples of cost functions

In this section, we'll discuss some common cost functions that are employed in both classification and regression tasks. Some of them will be repeatedly adopted in our examples over the next few chapters, particularly when we're discussing training processes in shallow and deep neural networks.

Mean squared error

Mean squared error is one of the most common regression cost functions. Its generic expression is:

This function is differentiable at every point of its domain and it's convex, so it can be optimized using the stochastic gradient descent (SGD) algorithm. This cost function is fundamental in regression analysis using the Ordinary or Generalized Least Square algorithms, where, for example, it's possible to prove that the estimators are always unbiased.

However, there's a drawback when employing it in regression tasks with outliers. Its value is always quadratic, and therefore, when the distance between the prediction and an actual outlier value is large, the relative error is large, and this can lead to an unacceptable correction.

Huber cost function

As explained, mean squared error isn't robust to outliers, because it's always quadratic, independent of the distance between actual value and prediction. To overcome this problem, it's possible to employ the Huber cost function, which is based on threshold t_H, so that for distances less than t_H its behavior is quadratic, while for a distance greater than t_H it becomes linear, reducing the entity of the error and thereby reducing the relative importance of the outliers.

The analytical expression is:

Hinge cost function

This cost function is adopted by Support Vector Machine (SVM) algorithms, where the goal is to maximize the distance between the separation boundaries, where the support vectors lie. Its analytic expression is:

Contrary to the other examples, this cost function is not optimized using classic SGD methods, because it's not differentiable when:

For this reason, SVM algorithms are optimized using quadratic programming techniques.

Categorical cross-entropy

Categorical cross-entropy is the most diffused classification cost function, adopted by logistic regression and the majority of neural architectures. The generic analytical expression is:

This cost function is convex and can easily be optimized using SGD techniques. According to information theory, the entropy of a distribution p is a measure of the amount of uncertainty—expressed in bit if is used and in nat is natural logarithm is employed—carried by a particular probability distribution. For example, if we toss a fair coin, then according to a Bernoulli distribution. Therefore, the entropy of such a discrete distribution is:

The uncertainty is equal to 1 bit, which means that before any experiment there are 2 possible outcomes, which is obvious. What happens if we know that the coin is loaded, and P(Head) = 0.1 and P(Tail) = 0.9? The entropy is now:

As our uncertainty is now very low—we know that in 90% of the cases, the outcome will be tails—the entropy is less than half a bit. The concept must be interpreted as a continuous measure, which means that a single outcome is very likely to appear. The extreme case when P(Head) → 0 and P(Tail) → 1 asymptotically requires 0 bits, because there's no more uncertainty and the probability distribution is degenerate.

The concept of entropy, as well as cross-entropy and other information theory formulas, can be extended to continuous distributions using an integral instead of a sum. For example, the entropy of a normal distribution is . In general, the entropy is proportional to the variance or to the spread of the distribution.

This is an intuitive concept, in fact; the larger the variance, the larger the region in which the potential outcomes have a similar probability to be selected. As the uncertainty grows when the potential set of candidate outcomes does, the price in bits or nats we need to pay to remove the uncertainty increases. In the example of the coin, we needed to pay 1 bit for a fair outcome and only 0.47 bit when we already knew that P(Tail) = 0.9; our uncertainty was quite a lot lower.

Analogously, cross-entropy is defined between two distributions p and q:

Let's suppose that p is the data generating process we are working with. What's the meaning of H(P, q)? Considering the expression, what we're doing is computing the expected value , while the entropy computed the expected value . Therefore, if q is an approximation of p, the cross-entropy measures the additional uncertainty that we are introducing when using the model q instead of the original data generating process. It's not difficult to understand that we increase the uncertainty by only using an approximation of the true underlying process.

In fact, if we're training a classifier, our goal is to create a model whose distribution is as similar as possible to p_data. This condition can be achieved by minimizing the Kullback-Leibler divergence between the two distributions:

In the previous expression, p_M is the distribution generated by the model. Now, if we rewrite the divergence, we get:

The first term is the entropy of the data generating distribution, and it doesn't depend on the model parameters, while the second one is the cross-entropy. Therefore, if we minimize the cross-entropy, we also minimize the Kullback-Leibler divergence, forcing the model to reproduce a distribution that is very similar to p_data. That means that we are reducing the additional uncertainty that was induced by the approximation. This is a very elegant explanation as to why the cross-entropy cost function is an excellent choice for classification problems.

Regularization

When a model is ill-conditioned or prone to overfitting, regularization offers some valid tools to mitigate the problems. From a mathematical viewpoint, a regularizer is a penalty added to the cost function, to impose an extra condition on the evolution of the parameters:

The parameter controls the strength of the regularization, which is expressed through the function . A fundamental condition on is that it must be differentiable so that the new composite cost function can still be optimized using SGD algorithms. In general, any regular function can be employed; however, we normally need a function that can contrast the indefinite growth of the parameters.

To understand the principle, let's consider the following diagram:

Interpolation with a linear curve (left) and a parabolic one (right)

In the first diagram, the model is linear and has two parameters, while in the second one, it is quadratic and has three parameters. We already know that the second option is more prone to overfitting, but if we apply a regularization term, it's possible to avoid the growth of the first quadratic parameter and transform the model into a linearized version.

Of course, there's a difference between choosing a lower-capacity model and applying a regularization constraint. In the first case, we are renouncing the possibility offered by the extra capacity with a consequent risk of large bias, while with regularization we keep the same model but optimize it to reduce the variance and only slightly increase the bias. I hope it's clear that regularization always leads to a suboptimal model M' and, in particular, if the original M is unbiased, M' will be biased proportionally to and to the kind of regularization used.

Generally speaking, if the absolute minimum of a cost function with respect to a training set is c_opt, any model with c > c_opt is suboptimal. This means that the training error is larger, but the generalization error might be better controlled.

In fact, a perfectly trained model could have learned the structure of the training set and reached a minimum loss, but, when a new sample is checked, the performance is much worse.

Even if it's not very mathematically rigorous, we can say that regularization often acts as a brake that avoids perfect convergence. By doing this, it keeps the model in a region where the generalization error is lower, which is, generally, the main objective of machine learning. Hence, this extra penalty can be accepted in the context of the bias-variance trade-off.

A small bias can be acceptable when it's the consequence of a drastic variance reduction (that is, a smaller generalization error); however, I strongly suggest that you don't employ regularization as a black-box technique, but instead to check (for example, using cross-validation) which value yields the optimal result, intended as a trade-off.

Examples of Regularization Techniques

At this point, we can explore the most common regularization techniques and discuss their properties.

L₂ or Ridge regularization

L₂ or Ridge regularization, also known as Tikhonov regularization, is based on the squared L₂-norm of the parameter vector:

This penalty avoids infinite growth of the parameters—for this reason, it's also known as weight shrinkage—and it's particularly useful when the model is ill-conditioned, or there is multicollinearity due to the fact that the samples are not completely independent, which is a relatively common condition.

In the following diagram, we see a schematic representation of the Ridge regularization in a bidimensional scenario:

 

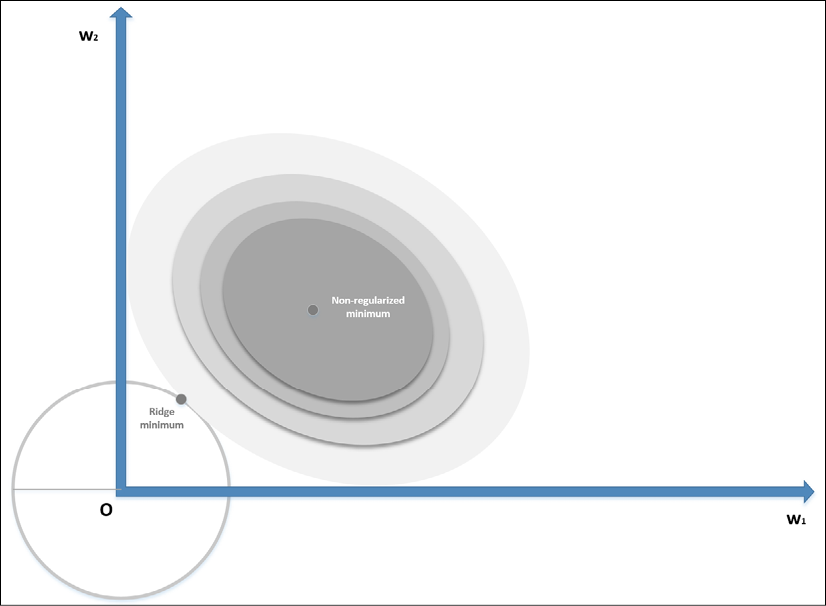
Ridge (L₂) regularization

The zero-centered circle represents the Ridge boundary, while the shaded surface is the original cost function. Without regularization, the minimum (w₁, w₂) has a magnitude (for example, the distance from the origin) which is about double the one obtained by applying a Ridge constraint, confirming the expected shrinkage.

When applied to regressions solved with the Ordinary Least Squares (OLS) algorithm, it's possible to prove that there always exists a Ridge coefficient, so that the weights are shrunk with respect to the OLS ones. The same result, with some restrictions, can be extended to other cost functions.

Moreover, Andrew Ng (in Ng A. Y., Feature selection, L1 vs. L2 regularization, and rotational invariance, ICML, 2004) proved that L₂ regularization, applied to the majority of classification algorithms, allows us to obtain rotational invariance. In other words, if the training set is rotated, a regularized model will yield the same prediction distribution as the original one. Another fundamental aspect to remember is that L₂-regularization shrinks the weights independent of the scale of the data. Therefore, if the features have different scales, the result may be worse than expected.

It's easy to understand this concept by considering a simple linear model with two variables, y = ax₁ + bx₁ + c. As the L₂ has a single control coefficient, the effect will be the same on both a and b (excluding the intercept c). If and , the shrinkage will affect x₁ much more than x₂.

For this reason, we recommend scaling the dataset before applying the regularization. Other important properties of this method will be discussed throughout the book, when specific algorithms are introduced.

L₁ or Lasso regularization

L₁ or Lasso regularization is based on the L₁-norm of the parameter vector:

While Ridge shrinks all the weights inversely proportionally to their importance, Lasso can shift the smallest weight to zero, creating a sparse parameter vector.

The mathematical proof is beyond the scope of this book; however, it's possible to understand it intuitively by considering the following bidimensional diagram:

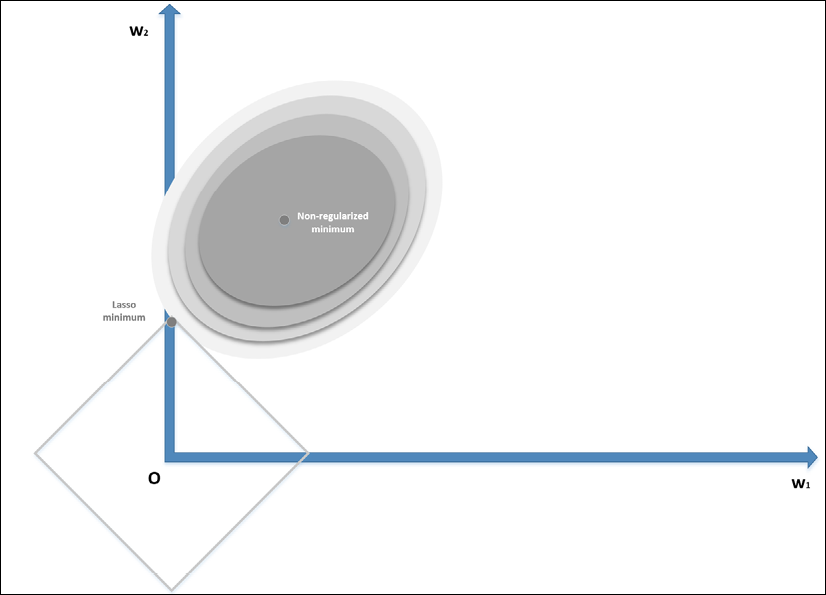
Lasso (L₁) regularization

The zero-centered square represents the Lasso boundaries in a bidimensional scenario (it will be a hyperdiamond in ). If we consider a generic line, the probability of that line being tangential to the square is higher at the corners, where at least one parameter is null—exactly one parameter in a bidimensional scenario. In general, if we have a vectorial convex function f(x) (we provide a definition of convexity in Chapter 7, Advanced Clustering and Unsupervised Models), we can define:

As any L_p-norm is convex, as well as the sum of convex functions, is also convex. The regularization term is always non-negative, and therefore the minimum corresponds to the norm of the null vector.

When minimizing , we also need to consider the contribution of the gradient of the norm in the ball centered in the origin, where the partial derivatives don't exist. Increasing the value of p, the norm becomes smoothed around the origin, and the partial derivatives approach zero for .

On the other hand, excluding the L₀-norm and all the norms with allows an even stronger sparsity, but is non-convex (even if L₀ is currently employed in the quantum algorithm QBoost). With p = 1 the partial derivatives are always +1 or -1, according to the sign of . Therefore, it's easier for the L₁-norm to push the smallest components to zero, because the contribution to the minimization (for example, with gradient descent) is independent of x_i, while an L₂-norm decreases its speed when approaching the origin.

This is a non-rigorous explanation of the sparsity achieved using the L₁-norm. In practice, we also need to consider the term , which bounds the value of the global minimum; however, it may help the reader to develop an intuitive understanding of the concept. It's possible to find further, more mathematically rigorous details in Sra S., Nowozin S., Wright S. J. (edited by), Optimization for Machine Learning, The MIT Press, 2011.

Lasso regularization is particularly useful when a sparse representation of a dataset is needed. For example, we could be interested in finding the feature vectors corresponding to a group of images. As we expect to have many features, but only a subset of those features present in each image, applying the Lasso regularization allows us to force all the smallest coefficients to become null, which helps us by suppressing the presence of the secondary features.

Another potential application is latent semantic analysis, where our goal is to describe the documents belonging to a corpus in terms of a limited number of topics. All these methods can be summarized in a technique called sparse coding, where the objective is to reduce the dimensionality of a dataset by extracting the most representative atoms, using different approaches to achieve sparsity.

Another important property of L₁ regularization concerns its ability to perform an implicit feature selection, induced by the sparsity. In a generic scenario, a dataset can also include irrelevant features that don't contribute to increasing the accuracy of the classification. This can happen because real-world datasets are often redundant, and the data collectors are more interested in their readability than in their usage for analytical purposes. There are many techniques (some of them are described in Bonaccorso G., Machine Learning Algorithms, Second Edition, Packt, 2018) that can be employed to select only those features that really transport unique pieces of information and discard the remaining ones; however, L₁ is particularly helpful.

First of all, it's automatic and no preprocessing steps are required. This is extremely useful in deep learning. Moreover, as Ng pointed out in the aforementioned paper, if a dataset contains n features, the minimum number of samples required to increase the accuracy over a predefined threshold is affected by the logarithm of the number of redundant or irrelevant features.

This means, for example, that if dataset X contains 1000 points and the optimal accuracy is achieved with this sample size when all the features are informative when k < p features are irrelevant, we need approximately 1000 + O(log k) samples. This is a simplification of the original result; for example, if p = 5000 and 500 features are irrelevant, assuming the simplest case, we need about data points.

Such a result is very important because it's often difficult and expensive to obtain a large number of new samples, in particular when they are obtained in experimental contexts (for example, social sciences, pharmacological research, and so on). Before moving on, let's consider a synthetic dataset containing 500 points with only five informative features:

from sklearn.datasets import make_classification

from sklearn.preprocessing import StandardScaler

X, Y = make_classification(n_samples=500, n_classes=2, n_features=10, n_informative=5,

n_redundant=3, n_clusters_per_class=2, random_state=1000)

ss = StandardScaler()

X_s = ss.fit_transform(X)

We can now fit two logistic regression instances with the whole dataset: the first one using the L₂ regularization and the second one using L₁. In both cases, the strength is kept fixed:

from sklearn.linear_model import LogisticRegression

lr_l2 = LogisticRegression(solver='saga', penalty='l2', C=0.25, random_state=1000)

lr_l1 = LogisticRegression(solver='saga', penalty='l1', C=0.25, random_state=1000)

lr_l2.fit(X_s, Y)

lr_l1.fit(X_s, Y)

It's possible to see that, in both cases, the 10-fold cross-validation yields approximately the same average accuracy. However, in this case, we are more interested in checking the feature selection properties of L₁; therefore we are going to compare the 10 coefficients of the two models, available as an instance variable coef_. The results are shown in the following figure:

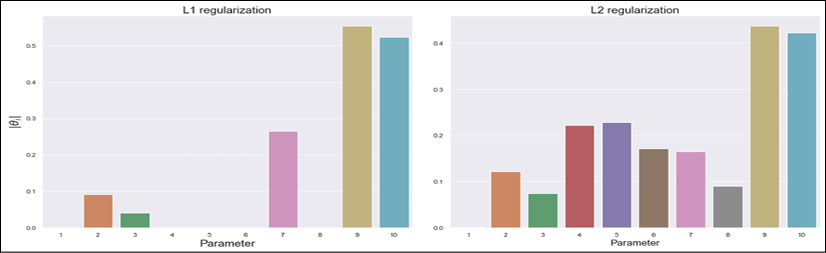
Logistic regression coefficients with L1 (left) and L2 (right) regularizations

As you can see, L₂ regularization tends to shrink all coefficients almost uniformly, excluding the dominance of 9 and 10, while L₁ performs a feature selection, by keeping only 5 non-null coefficients. This result is coherent with the structure of the dataset, in that it contains only 5 informative features and, therefore, a good classification algorithm can get rid of the remaining ones.

It's helpful to remember that we often need to create explainable models. That is to say, we often need to create models whose output can be immediately traced back to its causes. When there are many parameters, this task becomes more difficult. The usage of Lasso allows us to exclude all those features whose importance is secondary with respect to a primary group. In this way, the resulting model is smaller, and definitely more explainable.

As a general suggestion, in particular when working with linear models, I invite the reader to perform a feature selection to remove all non-determinant factors; and L₁ regularization is an excellent choice that avoids an additional preprocessing step.

Having discussed the main properties of both L₁ and L₂ regularizations, we can now explain how to combine them in order to exploit the respective benefits.

ElasticNet

In many real cases, it's useful to apply both Ridge and Lasso regularization in order to force weight shrinkage and a global sparsity. It is possible by employing the ElasticNet regularization, defined as:

The strength of each regularization is controlled by the parameters and . ElasticNet can yield excellent results whenever it's necessary to mitigate overfitting effects, while encouraging sparsity. We're going to apply all these regularization techniques when we discuss deep learning architectures.

Early stopping

Even though it's a pure regularization technique, early stopping is often considered a last resort when all other approaches to prevent overfitting, and maximize validation accuracy, fail. In many cases, above all in deep learning scenarios even though it can also happen with SVMs and other simpler classifiers, it's possible to observe a typical behavior of the training process, considering both training and the validation cost functions:

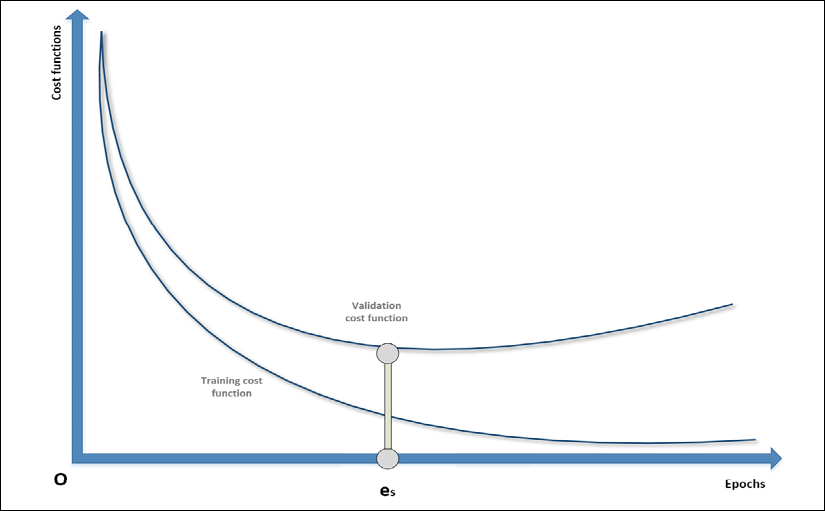
Example of early stopping before the beginning of the ascending phase of a U-curve

During the first epochs, both costs decrease, but it can happen that after a threshold epoch e_s, the validation cost starts increasing. If we continue with the training process, this results in overfitting the training set and increasing the variance.

For this reason, when there are no other options, it's possible to prematurely stop the training process. In order to do so, it's necessary to store the last parameter vector before the beginning of a new iteration and, in the case of no improvements or the accuracy worsening, to stop the process and recover the last set of parameters.

As explained, this procedure must never be considered as the best choice, because a better model or an improved dataset could yield higher performances. With early stopping, there's no way to verify alternatives, therefore it must be adopted only at the last stage of the process and never at the beginning.

Many deep learning frameworks such as Keras include helpers to implement early stopping callbacks. However, it's important to check whether the last parameter vector is the one stored before the last epoch or the one corresponding to e_s. In this case, it could be helpful to repeat the training process, stopping it at the epoch previous to e_s, where the minimum validation cost has been achieved.

Summary

In this chapter, we introduced the loss and cost functions, first as proxies of the expected risk, and then we detailed some common situations that can be experienced during an optimization problem. We also exposed some common cost functions, together with their main features and specific applications.

In the last part, we discussed regularization, explaining how it can mitigate the effects of overfitting and induce sparsity. In particular, the employment of Lasso can help the data scientist to perform automatic feature selection by forcing all secondary coefficients to become equal to 0.

In the next chapter, Chapter 3, Introduction to Semi-Supervised Learning, we're going to introduce semi-supervised learning, focusing our attention on the concepts of transductive and inductive learning.

Further reading

• Darwiche A., Human-Level Intelligence or Animal-Like Abilities?, Communications of the ACM, Vol. 61, 10/2018
• Crammer K., Kearns M., Wortman J., Learning from Multiple Sources, Journal of Machine Learning Research, 9/2008
• Mohri M., Rostamizadeh A., Talwalkar A., Foundations of Machine Learning, Second edition, The MIT Press, 2018
• Valiant L., A theory of the learnable, Communications of the ACM, 27, 1984
• Ng A. Y., Feature selection, L1 vs. L2 regularization, and rotational invariance, ICML, 2004
• Dube S., High Dimensional Spaces, Deep Learning and Adversarial Examples, arXiv:1801.00634 [cs.CV]
• Sra S., Nowozin S., Wright S. J. (edited by), Optimization for Machine Learning, The MIT Press, 2011
• Bonaccorso G., Machine Learning Algorithms, Second Edition, Packt, 2018