Chapter 11 Fundamentals of Detection Theory
‡ University of Illinois at Urbana-Champaign, USA
Detection problems arise in a number of engineering applications such as radar, communications, surveillance, and image analysis. In the basic setting of the problem, the goal is to detect the presence or absence of a signal in noise. This chapter will provide the mathematical and statistical foundations for solving such problems.
11.1.1 Statistical Decision Theory Framework
Detection problems fall under the umbrella of statistical decision theory [1], where the goal is to make a right (optimal) choice from a set of alternatives in a noisy environment. There are five basic ingredients in a typical decision theory problem.
• S
• D: The set of decisions or actions. This set is the set of decisions about the state. Elements in D would typically correspond to elements in S. In some applications such as communications with erasure, the set D could have larger cardinality than the set S. We denote a typical decision by the variable i, i.e., i ∈ D.
• C(i, j) or Ci,j: The cost function between decisions and states, C : D × S → ℝ+. In order to be able to talk about optimizing the decision, we need to quantify the cost incurred from each decision. The cost function C serves this purpose. An example of cost function, which is relevant in many applications, is the uniform cost function for which
(11.1) |
• Y: The set of observations. The decision about the state is not made blindly but based on some random observation1 Y taking values in Y.
• Δ: The set of decision rules or tests. Since the decisions are based on the observations, we need to have mappings from the observation set to the decision set. These are the decision rules, i.e., δ ∈ Δ, δ : Y ↦ D.
Detection problems are also referred to as hypothesis testing problems, with the understanding that each element of S corresponds to a hypothesis about the nature of the observations. The hypothesis corresponding to state j is denoted by Hj.
11.1.2 Probabilistic Structure for Observation Space
We associate with Y, a sigma algebra G of subsets of Y to which we assign probabilities. The pair (Y, G) is the observation space. In the applications of interest in this chapter, we will almost exclusively have Y = Rn, or Y = {γ1, γ2, …}, a countable set. In the case that Y = ℝn, we take G to be the smallest sigma-algebra containing all the n-dimensional rectangles in ℝn, i.e., the Borel sigma-algebra Bn. In the case when Y = {γ1, γ2, …}, we take G to be the power set of Y, i.e., 2Y.
For Y = Rn, we assume that probabilities can be assigned using an n-dimensional PDF. For Y = {γ1, γ2, …}, probabilities can be assigned using a PMF. We will use the term density for both PDFs and PMFs. We denote this density function by p, and use a common notation for the probability measure as in [2]:
For A ∈ G,
P(A) = ∫y∈Ap(y)μ(dy) = {∫y∈Ap(y)dyfor Y = ℝn∑γi∈Ap(γi) for Y = {γ1,γ2,…} |
(11.2) |
Let g be a function on Y. Then the expected value of the random variable g(Y) is given by
E[g(Y)] = ∫Yp(y)g(y)μ(dy) = {∫Yp(y)g(y)dyfor Y = ℝn∑Yp(γi)g(γi) for Y = {γ1,γ2,…} |
(11.3) |
11.1.3 Conditional Density and Conditional Risk
In order to make a decision about the state j based on the observation Y, we need to know how Y depends on j statistically. Typically, we assume that the conditional density (PDF/PMF) of Y conditioned on the state being j (which we denote by pj(y)) is available for each j ∈ S. In case the state is modeled as random variable J (see below), pj(y) is the usual conditional density pY∣J(y∣j), but otherwise we can think of the set {pj(y), j ∈ S} as simply an indexed set of densities, with pj being the density for Y that corresponds to the state being j.
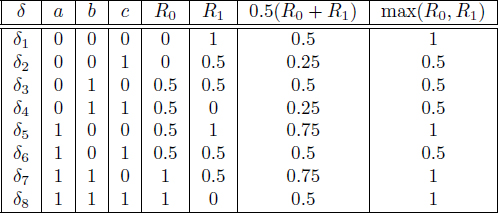
Table 11.1: Decision rules and conditional risks for Example 11.1.1.

The cost associated with a decision rule δ ∈ Δ is a random quantity (because Y is random) given by C(δ(Y), j). Therefore, to order decision rules according to their “merit” we use the quantity
Rj(δ) = Ej[C(δ(Y),j)] = ∫C(δ(y),j)pj(y)μ(dy).
which we call the conditional risk associated with δ when the state is j.
The conditional risk function can be used to obtain a (partial) ordering of the decision rules in Δ, in the following sense.
Definition 11.1.1. A decision rule δ is better than decision rule δ′ if
Rj(δ)≤Rj(δ′), ∀j∈S
and
Rj(δ)<Rj(δ′), for at least one j∈S
Sometimes it may be possible to find a decision rule δ* ∈ Δ which is better than any other δ ∈ Δ. In this case, the statistical decision problem is solved. Unfortunately, this usually happens only for trivial cases as in the following example.
Example 11.1.1. Suppose S = D = {0, 1} with the uniform cost function as in (11.1). Furthermore suppose the observation Y takes values in the set Y = {a, b, c} and the conditional p.m.f.’s of Y are:
p0(a) = 1,p0(b) = p0(c) = 0, p1(a) = 0,p1(b) = p1(c) = 0.5.
Then it is easy to see that we have the conditional risks for the eight possible decision rules depicted in Table 11.1. Clearly, δ4 is the best rule according to Definition 11.1.1, but this happens only because the conditional PMFs p0 and p1 have disjoint supports (see Exercise 2).
□
Since conditional risks cannot be used directly in finding optimal solutions to statistical decision making problems except in trivial cases, there are two general approaches for finding optimal decision rules: Bayesian and minimax.
Here we assume that we are given an a priori probability distribution on the set of states S. The state is then denoted by a random variable J with PMF {πj , j ∈ S} (since, for detection problems, the state space is finite). Now we introduce the average risk or Bayes risk associated with a decision rule δ, which is given by
(11.4) |
We can then obtain an ordering on the δ’s by using this Bayes risk. In particular, we choose the decision rule δB that has minimum Bayes risk, i.e.,
δB =argminδ∈Δr(δ).
The decision rule δB is called Bayes rule.
What if we are not given a prior distribution on the set S? We could postulate a distribution on S (for example, a uniform distribution) and use the Bayesian approach. On the other hand, one may want to guarantee a certain level of performance for all choices of state. In this case, we use a minimax approach. The goal of the minimax approach is to find the decision rule δm that has the best worst case cost:
δm = arg minδ∈Δ maxj∈S Rj(δ).
The decision rule δm is called the minimax rule.
In addition to Bayes and minimax approaches there are other criteria and techniques that are specific to special classes of decision-making problems. For example, in binary hypothesis testing, a third approach called the Neyman-Pearson approach (see Section 11.4) is often used in practice.
11.1.6 Randomized Decision Rules
Even though this might seem counter-intuitive at first, it is sometimes possible to get a better decision rule by randomly choosing between a set of deterministic decision rules.
Definition 11.1.2. A randomized decision rule δ̃ is described by
˜δ(y) = δl(y) with probability βl, l = 1,…,L
for some L and some {βℓ}, with βℓ > 0 and ∑ℓ ßℓ = 1.
Table 11.2: Decision rules, and Bayes and minimax risks for Example 11.1.2.
The set Δ̃ of randomized decision rules obviously contains the set Δ, and thus optimizing over Δ̃ will necessarily result in at least as good a decision rule as that obtained by optimizing over Δ.
Theorem 11.1.1. Randomization does not improve Bayes rules:
minδ∈Δ r(δ) = min˜δ∈˜Δ r(˜δ).
Proof: Since Δ ⊂ Δ̃, it is clear that the right-hand side (RHS) is less than or equal to the left-hand side (LHS). To prove the reverse inequality, suppose δ̃ chooses δℓ with probability βℓ, ℓ = 1, …, L. Then
r(˜δ) = L∑l = 1βl r(δl)≥L∑l = 1βlminδ∈Δ r(δ) = minδ∈Δ r(δ).
Taking the minimum over δ̃ ∈ Δ̃ on the LHS gives us the desired inequality.
■
However, as we see in the following example, randomization could result in a better minimax rule. We will also see later in Section 11.4 that randomization can yield better Neyman-Pearson rules for binary detection problems.
Example 11.1.2. Consider the same setup as in Example 11.1.1 with the following conditional PMF’s.
p0(a) = p0(b) = 0.5,p0(c) = 0, p1(a) = 0,p1(b) = p1(c) = 0.5.
We can compute the conditional risks for the eight possible decision rules as shown in Table 11.2. Clearly there is no “best” rule based on conditional risks alone in this case. Now consider finding a Bayes rule for priors π0 = π1 = 0.5. It is clear from the table that δ2 and δ4 are both Bayes rules. Also, δ2, δ3, δ4 and δ6 are all minimax rules with minimax risk equal to 0.5. Finally, randomizing between δ2 and δ4 with equal probability results in a rule with minimax risk equal to 0.25. Thus, we see that randomization can improve minimax rules.
□
11.1.7 General Method for Finding Bayes Rules
In the Bayesian framework, we can define the a posteriori probability π(j∣y) of the state j, given observation y. By Bayes probability law:
(11.5) |
We can write the Bayes risk of (11.4) in terms of π(j∣y) as:
r(δ) = E[E[C(δ(Y),J)|Y]] = ∫y∈Y[∑j∈Sπ(j|y)C(δ(y),j)]p(y)μ(dy). |
(11.6) |
Define the a posteriori cost of decision i ∈ D, given observation y, by
(11.7) |
Then it is easy to see that minimizing r(δ) in (11.6) is equivalent to minimizing C(δ(y)∣y) for each y. Thus
(11.8) |
11.2 Bayesian Binary Detection
We now study the special case of binary detection (hypothesis testing) in more detail. Here S = D = {0, 1}, and hence any deterministic decision rule δ partitions the observation space into disjoint sets Y0 and Y1, corresponding to decision δ(y) = 0 and δ(y) = 1, respectively. The conditional risks for a decision rule δ can be written as:
Rj(δ) = C0,jPj(Y0) + C1,jPj(Y1), j = 0,1.
Assumption 11.2.1. The cost of a correct decision about the state is strictly smaller than that of a wrong decision:
C0,0<C1,0, C1,1<C0,1.
Using (11.8), we can find a Bayes decision rule for binary detection as:
δB(y) = arg mini∈{0,1}C(i|y) = {1ifC(1|y)≤C(0|y)0ifC(1|y)>C(0|y).
Clearly, the Bayes solution need not be unique since the average risk is the same whether we assign the decision of “0” or “1” to observations for which C(1∣y) = C(0∣y). Using (11.7) and (11.5), we obtain:
δB(y) = {1if π(1|y)[C0,1 − C1,1]≥π(0|y)[C1,0 − C0,0]0otherwise |
(11.9) |
(11.10) |
Definition 11.2.1. The likelihood ratio is given by
L(y) = p1(y)p0(y), y∈Y
with the understanding that 00 = 0, and x0 = ∞, for x > 0.
If we further define the threshold τ by:
(11.11) |
then we can write
δB(y) = {1if L(y)≥τ0otherwise .
Thus Bayes rule is a “LRT.”
For uniform costs (see (11.1)), C0,0 = C1,1 = 0, and C0,1 = C1,0 = 1. Therefore, the threshold for the LRT simplifies to τ = π0π1 in this case. We can also see from (11.9) that
δB(y) = {1if π(1|y)≥π(0|y)0otherwise .
Thus, for uniform costs, Bayes rule is a MAP rule. Furthermore, for uniform costs, the Bayes risk of a decision rule δ is given by
r(δ) = π0P0(Y1) + π1P1(Y0).
The RHS is the average probability of error, denoted by Pe. Thus, for uniform costs, Bayes rule is also a minimum probability of error (MPE) rule.
Finally if we have uniform costs and equal priors (i.e., π0 = π1 = 0.5), then
δB(y) = {1if p1(y)≥p0(y)0otherwise
and Bayes rule is a maximum likelihood (ML) decision rule.
Example 11.2.1. Signal Detection in Gaussian Noise. This detection problem arises in a number of engineering applications, including radar and digital communications, and can be described by the hypotheses test:
H0:Y = μ0 + Z versus H1:Y = μ1 + Z
where the constants µ0 and µ1 represent deterministic signals, and Z is a zero mean Gaussian random variable with variance σ2, denoted by Z ~ N(0, σ2). Without loss of generality, we may assume that µ1 > µ0.
The conditional PDFs are given by:
pj(y) = 1√2πσ2 exp [ − (y − μj)22σ2], j = 0,1
and the likelihood ratio is given by:
L(y) = p1(y)p0(y) = exp [μ1 − μ0σ2(y − μ1 + μ02)].
It is easy to show that comparing L(y) to τ of (11.11) is equivalent to comparing y with τ′, where
τ′ = σ2μ1 − μ0log τ + μ1 + μ02.
Thus Bayes rule is equivalent to a threshold test on the observation y:
(11.12) |
For uniform costs and equal priors, τ = 1 and τ′ = μ1 + μ02. Furthermore,
r(δB) = Pe(δB) = 0.5P0(Y1) + 0.5P1(Y0)
where
P0(Y1) = P0{Y≥τ′} = 1 − Φ(τ′ − μ0σ) = 1 − Φ(μ1 − μ02σ) = Q(μ1 − μ02σ)
and
P1(Y0) = P1{Y<τ′} = Φ(τ′ − μ1σ) = Φ(μ0 − μ12σ) = Q(μ1 − μ02σ)
where Φ is CDF of a N(0, 1) random variable
(11.13) |
and Q is the complement of Φ, i.e., Q(x) = 1 − Φ(x) = Φ(− x), for x ∈ ℝ. Thus
r(δB) = Pe(δB) = Q(μ1 − μ02σ).
□
Example 11.2.2. Discrete Observations. Consider the detection problem of Example 11.1.2 with uniform costs, equal priors and
p0(a) = p0(b) = 0.5,p0(c) = 0, p1(a) = 0,p1(b) = p1(c) = 0.5.
The likelihood ratio is given by
L(y) = {0ify = a1ify = b∞ify = c.
With uniform costs and equal priors, the threshold τ = 1. Therefore
δB = {1ifL(y)≥10ifL(y)<1 = {1ify = b,c0ify = a.
This rule is nothing but δ4 of Example 11.1.2. Note that if we had chosen 0 when L(y) = τ, then we would have obtained δ2, which is also a Bayes rule.
□
Recall from Section 11.1.5 that the minimax decision rule δm minimizes the worst case risk:
δm = arg minδ∈Δ Rmax(δ).
where Rmax(δ) = max{R0(δ), R1(δ)}.
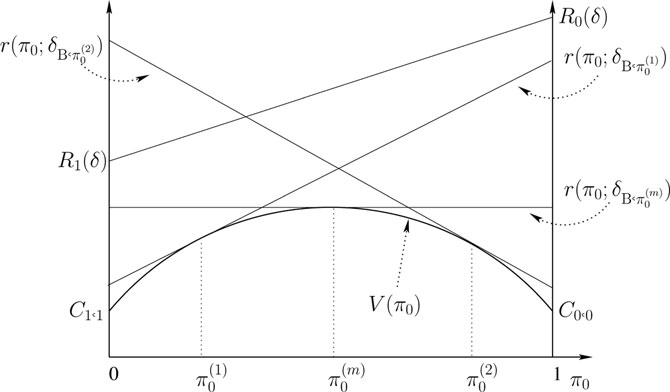
11.3.1 Bayes Risk Line and Minimum Risk Curve
We find δm indirectly by using the solution to Bayesian detection problem as follows. Since the prior on the states is not specified in the minimax setting, we allow the prior π0 (= 1 − π1) to be a variable over which we can optimize. We begin with the following definitions.
Definition 11.3.1. Bayes Risk Line. For any δ ∈ Δ,
r(π0;δ) = π0R0(δ) + (1 − π0)R1(δ).
Figure 11.1: Bayes risk lines and minimum risk curve.
Definition 11.3.2. Bayes Minimum Risk Curve.
V(π0) = minδ∈Δ r(π0;δ) = r(π0;δB,π0), π0∈[0,1]
where δB,π0 is a Bayes rule for prior π0.
Bayes risk lines and the minimum risk curve are illustrated in Figure 11.1. The following result states some useful properties of V(π0).
Lemma 11.3.1. V is a concave (continuous) function on [0, 1] with V(0) = C1,1 and V(1) = C0,0.
Proof: The minimum of concave functions is concave; therefore, the concavity of V follows from the fact that each of the risk lines r(π0; δ) is linear (and hence concave) in π0. As for the end point properties,
V(0) = minδ∈ΔR1(δ) = minδ∈ΔC0,1P1(Y0) + C1,1P1(Y1) = C1,1
where the minimizing rule is δ*(y) = 1, for all y ∈ Y. Similarly V(1) = C0,0.
■
We can write V(π0) in terms of the likelihood ratio L(y) and threshold τ as:
V(π0) = π0[C1,0P0{L(Y)≥τ} + C0,0P0{L(Y)<τ}] + (1 − π0)[C1,1P1{L(Y)≥τ} + C0,1P1{L(Y)<τ}].
If L(y) has no point masses2 under P0 or P1, then V is differentiable in π0 (since τ is differentiable in π0).
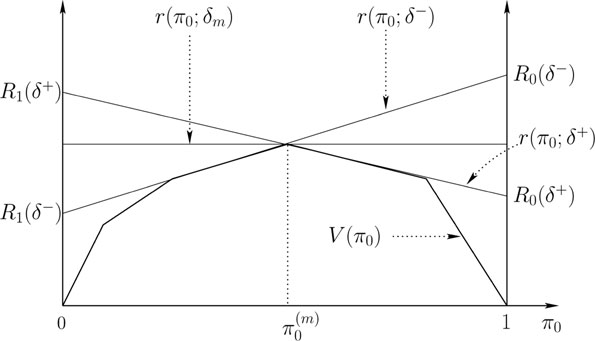
Figure 11.2: Minimax (equalizer) rule when V is differentiable at π(m)0.
Let us first consider the case where V is indeed differentiable for all π0. Then V(π0) achieves its maximum value at either the end points π0 = 0 or π0 = 1 or within the interior π0 ∈ (0, 1). If we assume uniform costs, then V(0) = V(1) = 0, and the maximum cannot be attained at the end points. Therefore, we further restrict our analysis to the case of uniform costs (the more general setting is considered in [2]).
Theorem 11.3.1. If C0,0 = C1,1 = 0 and V is differentiable on [0, 1], then
δm = δB,πm0
where πm0 = arg maxπ0V(π0), obtained by solving dV (π0)/dπ0 = 0, i.e., δm is a Bayes rule for the worst case prior. Furthermore, δm is a Bayes equalizer rule, i.e., R0(δm) = R1(δm). Note that randomization cannot improve the minimax rule in this case.
Proof: The proof follows from Figure 11.2 using the following steps:
1. For any δ ∈ Δ, the risk line r(π0; δ) cannot intersect with V(π0).
2. For fixed π(1)0, the risk line r(π0;δB,π(1)0) is tangent to V at π = π(1)0.
3. Any rule with risk line that is not tangential to V cannot be minimax because one can always find a rule with risk line that has the same slope and is tangential to V with smaller Rmax.
4. Among all Bayes rules, the one that has R0 = R1 is minimax.
Figure 11.3: Minimax rule when V is not differentiable at π(m)0.
Since the tangent to V at any fixed prior π0 is unique and corresponds to a deterministic Bayes rule for that prior, randomization cannot yield a better minimax rule.
■
If V is not differentiable for all π0, then the arguments given in the proof of Theorem 11.3.1 can still be used as long as V is differentiable at its maximum, and the minimax rule is still the unique Bayes rule for the worst case prior. If V is not differential at its maximum, then we have the scenario depicted in Figure 11.3. Note that δ− and δ+ are deterministic Bayes rules with same Bayes risk V(πm0), and since they are likelihood ratio tests with δ− having a larger risk under P0,
δ − = {1ifL(y)≥τ(πm0)0ifL(y)<τ(πm0), δ + = {1ifL(y)>τ(πm0)0ifL(y)≤τ(πm0)
where τ(πm0) = πm0/(1 − πm0). For δ− and δ+ to be different, L(Y) must have a point mass at τ(πm0), i.e., Pj{L(Y) = τ(πm0)}≠0, for j = 0, 1. This also implies that V is not differentiable at πm0. Also, if δ− and δ+ are different, then neither of them can be an equalizer rule.
Finding the minimax rule within the set of deterministic rules Δ is challenging in this case, since step 2 in the proof of Theorem 11.3.1 does not hold, and it is possible for a rule that has risk line that is not tangential to V to be minimax within Δ. We may need to resort to brute force enumeration to find minimax rules within Δ as we did in Example 11.1.2. Fortunately we can circumvent this problem by allowing for randomized decision rules.
It should be clear from Figure 11.3 that if an equalizer rule exists in Δ̃, which is tangential to V at πm0, then it must be minimax within the class Δ̃. Now, consider
˜δB,πm0 = {δ − with probability qδ + with probability (1 − q)
The conditional risks of this randomized decision rule are given by
R0(˜δB,πm0) = qR0(δ − ) + (1 − q)R0(δ + )R1(˜δB,πm0) = qR1(δ − ) + (1 − q)R1(δ + )
Thus, setting
q = R1(δ + ) − R0(δ + )(R1(δ + ) − R0(δ + )) + (R0(δ − ) − R1(δ − ))≜qm |
(11.14) |
produces an equalizer rule.
Theorem 11.3.2. If C0,0 = C1,1 = 0 and V is not differentiable at its maximum, then the minimax solution within the set of randomized decision rules Δ̃ is given by the equalizer rule:
˜δm = ˜δB,πm0 = {1ifL(y)>τ(πm0)1 w.p. qmifL(y) = τ(πm0)0ifL(y)<τ(πm0)
where πm0 = arg maxπ0V(π0) and qm is given in (11.14).
Example 11.3.1. Signal Detection in Gaussian Noise (continued). In this example we study the minimax solution to the detection problem described in Example 11.2.1. We assume uniform costs. We can compute the minimum Bayes risk curve as:
V(π0) = π0P0{Y≥τ′} + (1 − π0)P1{Y<τ′} = π0Q(τ′ − μ0σ) + (1 − π0)Φ(τ′ − μ1σ)
with
τ′ = σ2μ1 − μ0 log (π01 − π0) + μ1 + μ02.
Clearly V is a differentiable function, and therefore the deterministic equalizer rule is minimax. We can solve for the equalizer rule without explicitly maximizing V. In particular, if we denote the LRT with threshold τ′ (see (11.12)) by δτ′, then
R0(δτ′) = Q(τ′ − μ0σ), R1(δτ′) = Φ(τ′ − μ1σ) = Q(μ1 − τ′σ).
Setting R0(δτ′) = R1(δτ′) yields
τ′m = μ1 + μ02
from which we can conclude that τm = 1 and πm0 = 0.5.
Thus the minimax decision rule is given by
δm = δB,0.5 = {1if y≥μ1 + μ020otherwise
and the minimax risk is given by
r(δm) = V(0.5) = Q(μ1 − μ02σ).
□
Example 11.3.2. Discrete Observations (continued). In this example, we study the minimax solution to the detection problem described in Example 11.2.2. Recall that L(a) = 0, L(b) = 1, and L(c) = ∞. Assuming uniform costs, Bayes rules for prior π0 (randomized and deterministic) are given by:
˜δB,π0(y) = {1ifL(y)>τ(π0)1 w.p.qifL(y) = τ(π0)0ifL(y)<τ(π0) |
(11.15) |
where τ(π0) = π0/(1 − π0) and q ∈ [0, 1].
For π0 ∈ (0, 0.5), τ(π0) ∈ (0, 1), and thus all the Bayes rules in (11.15) collapse to the single deterministic rule:
δ − (y) = {1ify = b,c0ify = a.
Similarly, for π0 ∈ (0.5, 1), τ(π0) ∈ (1, ∞), and thus all the Bayes rules in (11.15) collapse to the single deterministic rule:
δ + (y) = {1ify = c0ify = a,b.
For π0 = 0.5, the following set of randomized decision rules are all Bayes rules:
˜δB,0.5(y) = {1ify = c1 w.p. qify = b0ify = a
Figure 11.4: Minimax rule for Example 11.3.2.
and these rules can be obtained by randomizing between δ+ and δ−. From the above discussion it is clear that the minimum Bayes risk curve V is as shown in Figure 11.4, with the worst case prior πm0 = 0.5. Furthermore, it is easy to check that R1(δ−) = R0(δ+) = 0, and R0(δ−) = R1(δ+) = 0.5. Therefore, from (11.14), qm = 0.5, and the minimax decision rule is given by:
˜δm = {1ify = c1 w.p. 0.5ify = b0ify = a
with minimax risk r(δ̃m) = V(0.5) = 0.25.
It is interesting to note that δ2 and δ4 in Example 11.1.2 are the same as δ+ and δ−, respectively, and that randomizing between these rules with equal probability is indeed the minimax solution within Δ̃.
□
11.4 Binary Neyman-Pearson Detection
For binary detection problems without a prior on the state, a commonly used alternative to minimax formulation is the Neyman-Pearson formulation, which is based on trading off the following two types of error probabilities:
Probability of False Alarm≜PF(˜δ) = P0{˜δ(Y) = 1} Probability of Miss≜PM(˜δ) = P1{˜δ(Y) = 0} |
(11.16) |
The goal is to minimize PM subject to the constraint PF ≤ α, for α ∈ (0, 1).
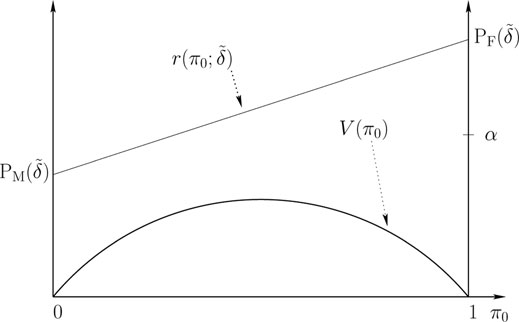
Figure 11.5: Risk line and Bayesian minimum risk curve for uniform costs.
An alternative measure of performance that is commonly used in radar and surveillance applications is:
Probability of Detection≜PD(˜δ) = P1{˜δ(Y) = 1} = 1 − PM(˜δ).
PD(δ̃) is also called the power of the decision rule δ̃. The Neyman-Pearson (N-P) problem is generally stated in terms PD and PF as:
(11.17) |
Note that unlike the Bayesian and minimax optimization problems, which are formulated in terms of conditional risks, the N-P optimization problem is stated in terms of conditional error probabilities. In particular, we are implicitly assuming uniform costs, which means PD(δ̃) = 1 ‒ R1(δ̃) and PF(δ̃) = R0(δ̃), and the N-P optimization is to minimize R1(δ̃) subject to R0(δ̃) ≤ α.
11.4.1 Solution to the N-P Optimization Problem
To solve the N-P optimization problem, we once again resort to Bayesian risk lines and the minimum risk curve V(π0) with uniform costs. As depicted in Figure 11.5, the risk line r(π0; δ̃) for any rule δ̃ ∈ Δ̃ lies above the concave function V(π0), and intersects the π0 = 0 line at level PM(δ̃) and the π0 = 1 line at level PF(δ̃). Among all decision rules with risk lines that have intersection with the π0 = 1 line at a level less than or equal to α, we are interested in the one which has the smallest intersection with the π0 = 0 line. As in the solution to the minimax problem, let us first consider the case where V is differentiable for all π0. Then it is clear that the decision rule that solves the N-P problem has a risk line that is tangential to V and intersects the π0 = 1 line at a level exactly equal to α. Such a rule is deterministic Bayes rule (LRT) that compares the likelihood ratio L(y) to a threshold η that satisfies the PF constraint.
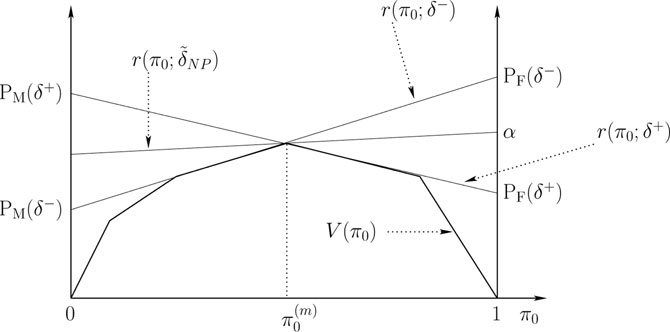
Figure 11.6: N-P optimization when V is not differentiable for all π0 ∈ [0, 1].
Theorem 11.4.1. if V is differentiable on [0, 1], then
˜δNP(y) = δη = {1if L(y)≥η0otherwise
where η is chosen so that P0{L(Y) ≥ η} = α.
Now consider the case where V is not differentiable, and we have the scenario depicted in Figure 11.6. The decision rule δ+ is the deterministic LRT that has the largest value of PF satisfying the constraint PF ≤ α, and the decision rule δ− is the other deterministic LRT for the same prior. By randomizing between δ+ and δ− we can produce a decision rule that has PF = α, and is hence a solution to (11.17).
Theorem 11.4.2. If V is not differentiable for all π0 ∈ [0, 1], then
˜δNP(y) = ˜δη,γ = {1ifL(y)>η1 w.p. γifL(y) = η0ifL(y)<η
where η and γ are chosen so that P0{L(Y) > η} + γP0{L(Y) = η} = α.
Figure 11.7: Complementary CDF of the likelihood ratio L(Y).
11.4.2 N-P Rule and Receiver Operating Characteristic
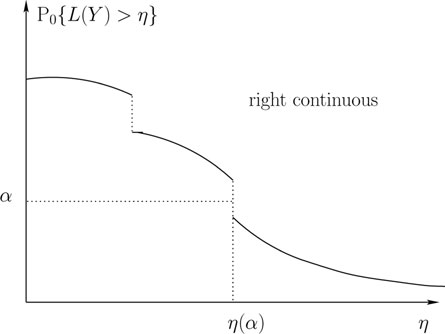
The procedure for finding the parameters η and γ of the Neyman-Pearson solution is illustrated in Figure 11.7, where we plot P0{L(y) > η} as a function of η. As seen in Figure 11.7, P0{L(y) > η} is a right continuous function of η. Given PF constraint α, we first choose η(α) as:
η(α) = min{η≥0:P0{L(y)>η}≤α}.
If P0{L(y) > η(α)} = α, then we do not need to randomize and we can set γ(α) = 0. If P0{L(y) > η(α)} < α, then we pick γ(α) so that
α = P0{L(y)>η(α)} + γ(α)P0{L(y) = η(α)}
which implies that
γ(α) = α − P0{L(y)>η(α)}P0{L(y) = η(α)}
The probability of detection (power) of δ̃NP for PF level α can be computed as:
PD(˜δNP) = P1{L(y)>η(α)} + γ(α)P1{L(y) = η(α)}.
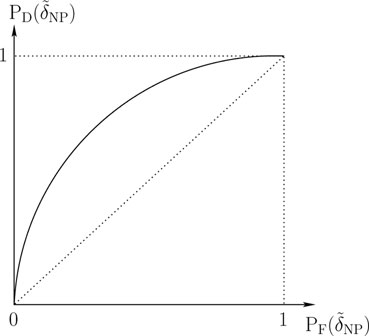
A plot of PD(δ̃NP) versus PF(δ̃NP) = α is called the receiver operating characteristics (ROC) of the Neyman-Pearson decision rule (see Figure 11.8). Some properties of the ROC are discussed in Exercise 11. In particular, the ROC is a concave function that lies above the 45° line, i.e., PD(δ̃NP) ≥ PF(δ̃NP).
Figure 11.8: Receiver operating characteristic (ROC).
Example 11.4.1. Signal Detection in Gaussian Noise (continued). In this example we study the N-P solution to the detection problem described in Example 11.2.1. As in the Bayesian setting of this problem, we can simplify the form of the LRT by noting that
L(y)η⇔y>η′ = σ2μ1 − μ0log η + μ1 + μ02
Thus
˜δNP(y) = {1ify>η′1 w.p. γify = η′0ify<η′.
Randomization is not needed since P0{Y = η′} = P1{Y = η′} = 0 for all η′ ∈ ℝ, and therefore
˜δNP(y) = δη′(y){1ify≥η′0ify<η′.
Now
PF(δη′) = P0{Y≥η′} = Q(η′ − μ0σ).
Therefore, we can meet a PF constraint of α by setting
η′(α) = σQ − 1(α) + μ0.
Figure 11.9: ROC for Example 11.4.1.
The power of δη′ is given by:
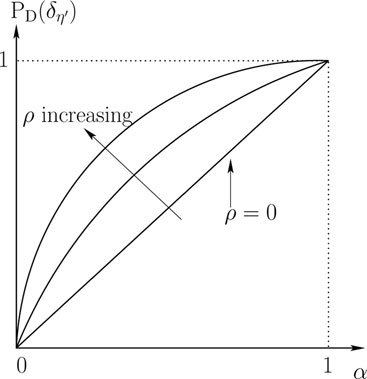
PD(δη′) = P1{Y≥η′} = Q(η′(α) − μ1σ) = Q(Q − 1(α) − ρ)
where ρ = (μ1 − μ0)/σ is a measure of the signal–to–noise ratio (SNR). The ROC is plotted in Figure 11.9. As ρ increases, the PD increases for a given level of PF.
□
Example 11.4.2. Discrete Observations (continued). In this example we study the N-P solution to the detection problem described in Example 11.2.2. Due to the fact that L(a) = 0, L(b) = 1, and L(c) = ∞, we have that
P0{L(Y>η} = {0.5ifη∈[0,1)0ifη∈[1,∞).
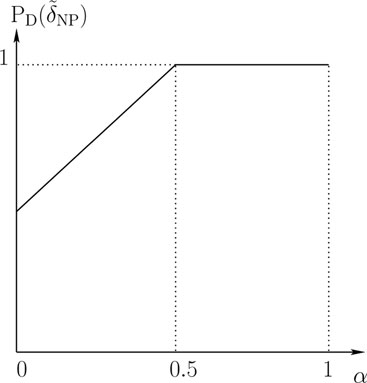
Thus, for α ∈ (0, 0.5), η(α) = 1 and γ(α) = α − 00.5 = 2α, which yields
˜δNP(y) = {1ify = c1 w.p. 2αify = b0ify = a
and
PD(˜δNP) = p1(c) + 2αp1(b) = 0.5 + α.
Figure 11.10: ROC for Example 11.4.2.
For α ∈ [0.5, 1), η(α) = 0 and γ(α) = α − 0.50.5 = 2α − 1, which yields
˜δNP(y) = {1 if y = c,b1 w.p. 2α − 1if y = a
and PD(δ̃NP) = 1. The ROC is plotted in Figure 11.10.
□
11.5 Bayesian Composite Detection
So far we have assumed that conditional densities p0 and p1 are specified completely. Under this assumption, we saw that all three formulations of the binary detection problem (Bayes, minimax, Neyman-Pearson) led to the same solution structure, LRT, which is a comparison of the likelihood ratio L(y) to an appropriately chosen threshold. We now study the situation where p0 and p1 are not specified explicitly, but we are told that they come from a parametrized family of densities {pθ, θ ∈ Λ}, with Λ being a discrete set or a subset of a Euclidean space. The hypothesis Hj corresponds to θ ∈ Λj, j = 0, 1, and Λ0 ∪ Λ1 = Λ, Λ0 ∩ Λ1 = 0.
We can consider composite binary detection (hypothesis testing) as a statistical decision theory problem where the set of states S = Λ is nonbinary, but the set of decisions D = {0, 1} is still binary, and the cost function relating the decisions and states is of the form:
(11.18) |
In this section we consider a Bayesian formulation of the problem, where we assume that the state θ is a realization of a random variable Θ with prior PDF (PMF) given by π(θ). From (11.8), we immediately have that Bayes rule for composite hypothesis testing is given by:
δB(y) arg mini∈DC(i|y)
where, using the notation introduced in (11.2),
C(i|y) = ∫θ∈ΛC(i,θ)p(θ|y)μ(dθ), with p(θ|y) = pθ(y)π(θ)p(y).
Using (11.18), we can expand C(i∣y) as:
C(i|y) = Ci,0∫θ∈Λ0p(θ|y)μ(dθ) + Ci,1∫θ∈Λ1p(θ|y)μ(dθ)
from which we can easily conclude that:
C(1|y)≤C(0|y)⇔∫θ∈Λ1pθ(y)π(θ)μ(dθ)∫θ∈Λ0pθ(y)π(θ)μ(dθ)≥C1,0 − C0,0C0,1 − C1,1. |
(11.19) |
Now, if we define the priors on the hypotheses as
(11.20) |
and the conditional densities for the hypotheses as
p(y|Λj)≜1πj∫θ∈Λjpθ(y)π(θ)μ(dθ)
then we can see that
C(1|y)≤C(0|y)⇔L(y)≥τ
with τ as defined in (11.11) and L(y) = p(y∣Λ1)/p(y∣Λ0).
Therefore, we can conclude that Bayes rule for composite detection is nothing but a LRT for the (simple) binary detection problem:
H0:Y~p(y|Λ0) versus H1:Y~p(y|Λ1)
with priors π0 and π1 as defined in (11.20).
Example 11.5.1. Consider the composite detection problem in which Λ = [0, ∞), Λ0 = [0, 1), and Λ1 = [1, ∞), with uniform costs, and
pθ(y) = θe − θyI{y≥0}, π(θ) = e − θI{θ≥0}
where I is the indicator function. To compute the Bayes rule for this problem, we first compute
∫θ∈Λ1pθ(y)π(θ)μ(dθ) = ∫∞1θe − θ(y + 1)dθ = (y + 2)e − (y + 1)(y + 1)2
and
∫θ∈Λ0pθ(y)π(θ)μ(dθ) = ∫10θe − θ(y + 1)dθ = 1 − (y + 2)e − (y + 1)(y + 1)2.
Then, from (11.19), we get that
δB = {1if (y + 2)≥0.5e(y + 1)0otherwise
which can be simplified to
δB = {1if 0≤y≤τ′0if y>τ′
where τ′ is a solution to the transcendental equation (y + 2) = 0.5e(y+1).
□
11.6 Neyman-Pearson Composite Detection
We now consider the more interesting setting for the composite detection problem where there is no prior on the state. A common way to pose the optimization problem in this setting is a generalization of the Neyman-Pearson formulation (see (11.16)). We define the probabilities of false alarm and detection of a test δ̃ ∈ Δ̃ by:
PF(˜δ;θ) = Pθ{˜δ(Y) = 1}, θ∈Λ0PD(˜δ;θ) = P1{˜δ(Y) = 1}, θ∈Λ1
The goal in UMP detection is to constrain PF(δ̃; θ) ≤ α, for all θ ∈ Λ0, and to simultaneously maximize PD(δ̃; θ), for all θ ∈ Λ1. If such a test exists, it is called UMP.
11.6.1 UMP Detection with One Composite Hypothesis
We begin by studying the special case where only H1 is composite, i.e., Λ0 is the singleton set equal to {θ0}. The UMP optimization problem can be stated as:
Maximize PD(˜δ;θ),for allθ∈Λ1, subject toPF(˜δ;θ0)≤α.
For fixed θ1 ∈ Λ1, we can compute the likelihood ratio as
Lθ1(y) = pθ1(y)pθ0(y)
and the corresponding Neyman-Pearson test is given by (see Theorem 11.4.2)
˜δNP(y;θ1) = {1ifLθ1(y)>ηα(θ1)1 w.p. γα(θ1)ifLθ1(y) = ηα(θ1)0ifLθ1(y)<ηα(θ1)
with γα(θ1) and γα(θ1) satisfying
Pθ0{L(Y)>ηα(θ1)} + γα(θ1)Pθ0{L(Y) = ηα(θ1)} = α.
Now, if it turns out that δ̃NP(y; θ1) is independent of θ1, then that test is UMP since it is the N-P solution for all θ1 ∈ Λ1. Otherwise, no UMP solution exists. In the following, we provide some illustrative examples.
Example 11.6.1. Detection of One-Sided Composite Signal in Gaussian Noise. This detection problem arises in communications and radar applications where the signal amplitude is unknown but the phase is known. The two hypotheses are described by:
H0:Y = Z versus H1:Y = θ + Z
where θ > 0 is an unknown parameter (signal amplitude), and Z ~ N(0, σ2). This is a composite detection problem with θ0 = 0, and Λ1 = (0, ∞).
For fixed θ > 0, Lθ(y) = pθ(y)/p0(y) has no point masses under P0 or Pθ, and therefore δ̃NP(y; θ) is deterministic LRT:
δNP(y;θ) = {1ifLθ(y)≥η(θ)0ifLθ(y)<η(θ) = {1ify≥η′(θ)0ify<η′(θ)
where (see Example 11.4.1) η′(θ) is given by
η′(θ) = σ2log η(θ)θ + θ2.
For an α-level test we need to find η′α(θ) such that P0{Y ≥ η′α(θ)} = α. Exploiting the fact that Y ~ N(0, σ2) under P0, we get
Q(η′α(θ)σ) = α ⇒ η′α(θ) = σQ − 1(α).
Note that η′α(θ) is independent of θ, and therefore the UMP solution is given by:
δUMP = {1ify≥σQ − 1(α)0ify<σQ − 1(α).
Note that while the test δUMP is independent of the θ, the performance of the test in terms of the PD depends strongly on θ. In particular,
PD(δUMP;θ) = Pθ{Y≥σQ − 1(α)} = Q(Q − 1(α) − θ/σ).
□
Example 11.6.2. Detection of Two-Sided Composite Signal in Gaussian Noise. This detection problem arises in communications and radar applications where the signal amplitude and phase are both unknown. The two hypotheses are as described in Example 11.6.1, except that θ ∈ ℝ, i.e., θ can be both positive and negative. There is no UMP test for this problem. This can be seen as follows.
First consider θ = 1. Then following the same steps as in Example 11.6.1, we can show that the α-level N-P test is given by:
δNP(y;1) = {1ify≥σQ − 1(α)0ify<σQ − 1(α).
Now, consider θ = −1. Then, it is not difficult to see that L−1(y) ≥ η iff y ≤ η′ in this case. Therefore the α-level N-P test is given by:
δNP(y; − 1) = {1ify≤σΦ − 1(α)0ify<σΦ − 1(α).
Since the most powerful tests for θ = −1 and θ = 1 are not the same, there is no uniformly most powerful test.
Example 11.6.3. Detection of One-Sided Composite Signal in Cauchy Noise. From Examples 11.6.1 and 11.6.2, we may be tempted to conclude that for problems involving signal detection in noise, UMP tests exist as long as H1 is one-sided. To see that this is not true in general, we consider the example where the noise has a Cauchy distribution, i.e.,
pθ(y) = 1π[1 + (y − θ)2]
and we are testing H0 : θ = 0 against the one-sided composite hypothesis H1 : θ > 0. Then
Lθ(y) = 1 + y21 + (y − θ)2.
It is easy to check that the α-level N-P tests for θ = 1 and θ = 2 are different, and hence there is no UMP solution.
□