Image processing is a difficult task for many types of machine learning algorithms. The relationships linking patterns of pixels to higher concepts are extremely complex and hard to define. For instance, it's easy for a human being to recognize a face, a cat, or the letter "A", but defining these patterns in strict rules is difficult. Furthermore, image data is often noisy. There can be many slight variations in how the image was captured, depending on the lighting, orientation, and positioning of the subject.
SVMs are well-suited to tackle the challenges of image data. Capable of learning complex patterns without being overly sensitive to noise, they are able to recognize visual patterns with a high degree of accuracy. Moreover, the key weakness of SVMs—the black box model representation—is less critical for image processing. If an SVM can differentiate a cat from a dog, it does not matter much how it is doing so.
In this section, we will develop a model similar to those used at the core of the Optical Character Recognition (OCR) software often bundled with desktop document scanners. The purpose of such software is to process paper-based documents by converting printed or handwritten text into an electronic form to be saved in a database. Of course, this is a difficult problem due to the many variants in handwritten style and printed fonts. Even so, software users expect perfection, as errors or typos can result in embarrassing or costly mistakes in a business environment. Let's see whether our SVM is up to the task.
When OCR software first processes a document, it divides the paper into a matrix such that each cell in the grid contains a single glyph, which is just a term referring to a letter, symbol, or number. Next, for each cell, the software will attempt to match the glyph to a set of all characters it recognizes. Finally, the individual characters would be combined back together into words, which optionally could be spell-checked against a dictionary in the document's language.
In this exercise, we'll assume that we have already developed the algorithm to partition the document into rectangular regions each consisting of a single character. We will also assume the document contains only alphabetic characters in English. Therefore, we'll simulate a process that involves matching glyphs to one of the 26 letters, A through Z.
To this end, we'll use a dataset donated to the UCI Machine Learning Data Repository (http://archive.ics.uci.edu/ml) by W. Frey and D. J. Slate. The dataset contains 20,000 examples of 26 English alphabet capital letters as printed using 20 different randomly reshaped and distorted black and white fonts.
The following figure, published by Frey and Slate, provides an example of some of the printed glyphs. Distorted in this way, the letters are challenging for a computer to identify, yet are easily recognized by a human being:
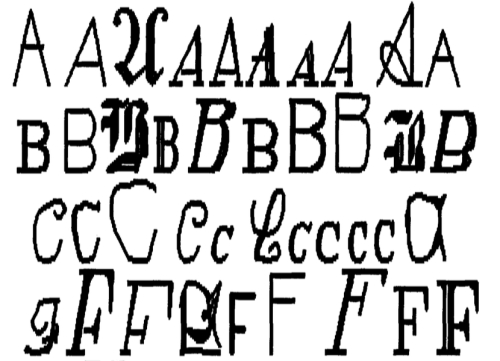
According to the documentation provided by Frey and Slate, when the glyphs are scanned into the computer, they are converted into pixels and 16 statistical attributes are recorded.
The attributes measure such characteristics as the horizontal and vertical dimensions of the glyph, the proportion of black (versus white) pixels, and the average horizontal and vertical position of the pixels. Presumably, differences in the concentration of black pixels across various areas of the box should provide a way to differentiate among the 26 letters of the alphabet.
Reading the data into R, we confirm that we have received the data with the 16 features that define each example of the letter class. As expected, letter has 26 levels:
> letters <- read.csv("letterdata.csv") > str(letters) 'data.frame': 20000 obs. of 17 variables: $ letter: Factor w/ 26 levels "A","B","C","D",.. $ xbox : int 2 5 4 7 2 4 4 1 2 11 ... $ ybox : int 8 12 11 11 1 11 2 1 2 15 ... $ width : int 3 3 6 6 3 5 5 3 4 13 ... $ height: int 5 7 8 6 1 8 4 2 4 9 ... $ onpix : int 1 2 6 3 1 3 4 1 2 7 ... $ xbar : int 8 10 10 5 8 8 8 8 10 13 ... $ ybar : int 13 5 6 9 6 8 7 2 6 2 ... $ x2bar : int 0 5 2 4 6 6 6 2 2 6 ... $ y2bar : int 6 4 6 6 6 9 6 2 6 2 ... $ xybar : int 6 13 10 4 6 5 7 8 12 12 ... $ x2ybar: int 10 3 3 4 5 6 6 2 4 1 ... $ xy2bar: int 8 9 7 10 9 6 6 8 8 9 ... $ xedge : int 0 2 3 6 1 0 2 1 1 8 ... $ xedgey: int 8 8 7 10 7 8 8 6 6 1 ... $ yedge : int 0 4 3 2 5 9 7 2 1 1 ... $ yedgex: int 8 10 9 8 10 7 10 7 7 8 ...
Recall that SVM learners require all features to be numeric, and moreover, that each feature is scaled to a fairly small interval. In this case, every feature is an integer, so we do not need to convert any factors into numbers. On the other hand, some of the ranges for these integer variables appear fairly wide. This indicates that we need to normalize or standardize the data. However, we can skip this step for now, because the R package that we will use for fitting the SVM model will perform the rescaling automatically.
Given that the data preparation has been largely done for us, we can move directly to the training and testing phases of the machine learning process. In the previous analyses, we randomly divided the data between the training and testing sets. Although we could do so here, Frey and Slate have already randomized the data, and therefore suggest using the first 16,000 records (80 percent) to build the model and the next 4,000 records (20 percent) to test. Following their advice, we can create training and testing data frames as follows:
> letters_train <- letters[1:16000, ] > letters_test <- letters[16001:20000, ]
With our data ready to go, let's start building our classifier.
When it comes to fitting an SVM model in R, there are several outstanding packages to choose from. The e1071 package from the Department of Statistics at the Vienna University of Technology (TU Wien) provides an R interface to the award winning LIBSVM library, a widely used open source SVM program written in C++. If you are already familiar with LIBSVM, you may want to start here.
Note
For more information on LIBSVM, refer to the authors' website at http://www.csie.ntu.edu.tw/~cjlin/libsvm/.
Similarly, if you're already invested in the SVMlight algorithm, the klaR package from the Department of Statistics at the Dortmund University of Technology (TU Dortmund) provides functions to work with this SVM implementation directly within R.
Note
For information on SVMlight, have a look at http://svmlight.joachims.org/.
Finally, if you are starting from scratch, it is perhaps best to begin with the SVM functions in the kernlab package. An interesting advantage of this package is that it was developed natively in R rather than C or C++, which allows it to be easily customized; none of the internals are hidden behind the scenes. Perhaps even more importantly, unlike the other options, kernlab can be used with the caret package, which allows SVM models to be trained and evaluated using a variety of automated methods (covered in Chapter 11, Improving Model Performance).
Note
For a more thorough introduction to
kernlab, please refer to the authors' paper at http://www.jstatsoft.org/v11/i09/.
The syntax for training SVM classifiers with kernlab is as follows. If you do happen to be using one of the other packages, the commands are largely similar. By default, the ksvm() function uses the Gaussian RBF kernel, but a number of other options are provided.

To provide a baseline measure of SVM performance, let's begin by training a simple linear SVM classifier. If you haven't already, install the kernlab package to your library, using the install.packages("kernlab") command. Then, we can call the ksvm() function on the training data and specify the linear (that is, vanilla) kernel using the vanilladot option, as follows:
> library(kernlab) > letter_classifier <- ksvm(letter ~ ., data = letters_train, kernel = "vanilladot")
Depending on the performance of your computer, this operation may take some time to complete. When it finishes, type the name of the stored model to see some basic information about the training parameters and the fit of the model.
> letter_classifier Support Vector Machine object of class "ksvm" SV type: C-svc (classification) parameter : cost C = 1 Linear (vanilla) kernel function. Number of Support Vectors : 7037 Objective Function Value : -14.1746 -20.0072 -23.5628 -6.2009 -7.5524 -32.7694 -49.9786 -18.1824 -62.1111 -32.7284 -16.2209... Training error : 0.130062
This information tells us very little about how well the model will perform in the real world. We'll need to examine its performance on the testing dataset to know whether it generalizes well to unseen data.
The predict() function allows us to use the letter classification model to make predictions on the testing dataset:
> letter_predictions <- predict(letter_classifier, letters_test)
Because we didn't specify the type parameter, the type = "response" default was used. This returns a vector containing a predicted letter for each row of values in the test data. Using the head() function, we can see that the first six predicted letters were U, N, V, X, N, and H:
> head(letter_predictions) [1] U N V X N H Levels: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
To examine how well our classifier performed, we need to compare the predicted letter to the true letter in the testing dataset. We'll use the table() function for this purpose (only a portion of the full table is shown here):
> table(letter_predictions, letters_test$letter) letter_predictions A B C D E A 144 0 0 0 0 B 0 121 0 5 2 C 0 0 120 0 4 D 2 2 0 156 0 E 0 0 5 0 127
The diagonal values of 144, 121, 120, 156, and 127 indicate the total number of records where the predicted letter matches the true value. Similarly, the number of mistakes is also listed. For example, the value of 5 in row B and column D indicates that there were five cases where the letter D was misidentified as a B.
Looking at each type of mistake individually may reveal some interesting patterns about the specific types of letters the model has trouble with, but this is time consuming. We can simplify our evaluation instead by calculating the overall accuracy. This considers only whether the prediction was correct or incorrect, and ignores the type of error.
The following command returns a vector of TRUE or FALSE values, indicating whether the model's predicted letter agrees with (that is, matches) the actual letter in the test dataset:
> agreement <- letter_predictions == letters_test$letter
Using the table() function, we see that the classifier correctly identified the letter in 3,357 out of the 4,000 test records:
> table(agreement) agreement FALSE TRUE 643 3357
In percentage terms, the accuracy is about 84 percent:
> prop.table(table(agreement)) agreement FALSE TRUE 0.16075 0.83925
Note that when Frey and Slate published the dataset in 1991, they reported a recognition accuracy of about 80 percent. Using just a few lines of R code, we were able to surpass their result, although we also have the benefit of over two decades of additional machine learning research. With this in mind, it is likely that we are able to do even better.
Our previous SVM model used the simple linear kernel function. By using a more complex kernel function, we can map the data into a higher dimensional space, and potentially obtain a better model fit.
It can be challenging, however, to choose from the many different kernel functions. A popular convention is to begin with the Gaussian RBF kernel, which has been shown to perform well for many types of data. We can train an RBF-based SVM, using the ksvm() function as shown here:
> letter_classifier_rbf <- ksvm(letter ~ ., data = letters_train, kernel = "rbfdot")
Next, we make predictions as done earlier:
> letter_predictions_rbf <- predict(letter_classifier_rbf, letters_test)
Finally, we'll compare the accuracy to our linear SVM:
> agreement_rbf <- letter_predictions_rbf == letters_test$letter > table(agreement_rbf) agreement_rbf FALSE TRUE 275 3725 > prop.table(table(agreement_rbf)) agreement_rbf FALSE TRUE 0.06875 0.93125
By simply changing the kernel function, we were able to increase the accuracy of our character recognition model from 84 percent to 93 percent. If this level of performance is still unsatisfactory for the OCR program, other kernels could be tested, or the cost of constraints parameter C could be varied to modify the width of the decision boundary. As an exercise, you should experiment with these parameters to see how they impact the success of the final model.

