Think back to the last time you made an impulse purchase. Maybe you were waiting in the grocery store checkout lane and bought a pack of chewing gum or a candy bar. Perhaps on a late-night trip for diapers and formula you picked up a caffeinated beverage or a six-pack of beer. You might have even bought this book on a whim on a bookseller's recommendation. These impulse buys are no coincidence, as retailers use sophisticated data analysis techniques to identify patterns that will drive retail behavior.
In years past, such recommendation systems were based on the subjective intuition of marketing professionals and inventory managers or buyers. More recently, as barcode scanners, computerized inventory systems, and online shopping trends have built a wealth of transactional data, machine learning has been increasingly applied to learn purchasing patterns. The practice is commonly known as market basket analysis due to the fact that it has been so frequently applied to supermarket data.
Although the technique originated with shopping data, it is useful in other contexts as well. By the time you finish this chapter, you will be able to apply market basket analysis techniques to your own tasks, whatever they may be. Generally, the work involves:
- Using simple performance measures to find associations in large databases
- Understanding the peculiarities of transactional data
- Knowing how to identify the useful and actionable patterns
The results of a market basket analysis are actionable patterns. Thus, as we apply the technique, you are likely to identify applications to your work, even if you have no affiliation with a retail chain.
The building blocks of a market basket analysis are the items that may appear in any given transaction. Groups of one or more items are surrounded by brackets to indicate that they form a set, or more specifically, an itemset that appears in the data with some regularity. Transactions are specified in terms of itemsets, such as the following transaction that might be found in a typical grocery store:
The result of a market basket analysis is a collection of association rules that specify patterns found in the relationships among items he itemsets. Association rules are always composed from subsets of itemsets and are denoted by relating one itemset on the left-hand side (LHS) of the rule to another itemset on the right-hand side (RHS) of the rule. The LHS is the condition that needs to be met in order to trigger the rule, and the RHS is the expected result of meeting that condition. A rule identified from the example transaction might be expressed in the form:
In plain language, this association rule states that if peanut butter and jelly are purchased together, then bread is also likely to be purchased. In other words, "peanut butter and jelly imply bread."
Developed in the context of retail transaction databases, association rules are not used for prediction, but rather for unsupervised knowledge discovery in large databases. This is unlike the classification and numeric prediction algorithms presented in previous chapters. Even so, you will find that association rule learners are closely related to and share many features of the classification rule learners presented in Chapter 5, Divide and Conquer – Classification Using Decision Trees and Rules.
Because association rule learners are unsupervised, there is no need for the algorithm to be trained; data does not need to be labeled ahead of time. The program is simply unleashed on a dataset in the hope that interesting associations are found. The downside, of course, is that there isn't an easy way to objectively measure the performance of a rule learner, aside from evaluating them for qualitative usefulness—typically, an eyeball test of some sort.
Although association rules are most often used for market basket analysis, they are helpful for finding patterns in many different types of data. Other potential applications include:
- Searching for interesting and frequently occurring patterns of DNA and protein sequences in cancer data
- Finding patterns of purchases or medical claims that occur in combination with fraudulent credit card or insurance use
- Identifying combinations of behavior that precede customers dropping their cellular phone service or upgrading their cable television package
Association rule analysis is used to search for interesting connections among a very large number of elements. Human beings are capable of such insight quite intuitively, but it often takes expert-level knowledge or a great deal of experience to do what a rule learning algorithm can do in minutes or even seconds. Additionally, some datasets are simply too large and complex for a human being to find the needle in the haystack.
Just as it is challenging for humans, transactional data makes association rule mining a challenging task for machines as well. Transactional datasets are typically extremely large, both in terms of the number of transactions as well as the number of items or features that are monitored. The problem is that the number of potential itemsets grows exponentially with the number of features. Given k items that can appear or not appear in a set, there are 2^k possible itemsets that could be potential rules. A retailer that sells only 100 different items could have on the order of 2^100 = 1.27e+30 itemsets that an algorithm must evaluate—a seemingly impossible task.
Rather than evaluating each of these itemsets one by one, a smarter rule learning algorithm takes advantage of the fact that, in reality, many of the potential combinations of items are rarely, if ever, found in practice. For instance, even if a store sells both automotive items and women's cosmetics, a set of {motor oil, lipstick} is likely to be extraordinarily uncommon. By ignoring these rare (and, perhaps, less important) combinations, it is possible to limit the scope of the search for rules to a more manageable size.
Much work has been done to identify heuristic algorithms for reducing the number of itemsets to search. Perhaps the most-widely used approach for efficiently searching large databases for rules is known as Apriori. Introduced in 1994 by Rakesh Agrawal and Ramakrishnan Srikant, the Apriori algorithm has since become somewhat synonymous with association rule learning. The name is derived from the fact that the algorithm utilizes a simple prior (that is, a priori) belief about the properties of frequent itemsets.
Before we discuss that in more depth, it's worth noting that this algorithm, like all learning algorithms, is not without its strengths and weaknesses. Some of these are listed as follows:
|
Strengths |
Weaknesses |
|---|---|
|
As noted earlier, the Apriori algorithm employs a simple a priori belief to reduce the association rule search space: all subsets of a frequent itemset must also be frequent. This heuristic is known as the Apriori property. Using this astute observation, it is possible to dramatically limit the number of rules to be searched. For example, the set {motor oil, lipstick} can only be frequent if both {motor oil} and {lipstick} occur frequently as well. Consequently, if either motor oil or lipstick is infrequent, any set containing these items can be excluded from the search.
To see how this principle can be applied in a more realistic setting, let's consider a simple transaction database. The following table shows five completed transactions in an imaginary hospital's gift shop:
|
Transaction number |
Purchased items |
|---|---|
|
1 |
{flowers, get well card, soda} |
|
2 |
{plush toy bear, flowers, balloons, candy bar} |
|
3 |
{get well card, candy bar, flowers} |
|
4 |
{plush toy bear, balloons, soda} |
|
5 |
{flowers, get well card, soda} |
By looking at the sets of purchases, one can infer that there are a couple of typical buying patterns. A person visiting a sick friend or family member tends to buy a get well card and flowers, while visitors to new mothers tend to buy plush toy bears and balloons. Such patterns are notable because they appear frequently enough to catch our interest; we simply apply a bit of logic and subject matter experience to explain the rule.
In a similar fashion, the Apriori algorithm uses statistical measures of an itemset's "interestingness" to locate association rules in much larger transaction databases. In the sections that follow, we will discover how Apriori computes such measures of interest and how they are combined with the Apriori property to reduce the number of rules to be learned.
Whether or not an association rule is deemed interesting is determined by two statistical measures: support and confidence measures. By providing minimum thresholds for each of these metrics and applying the Apriori principle, it is easy to drastically limit the number of rules reported, perhaps even to the point where only the obvious or common sense rules are identified. For this reason, it is important to carefully understand the types of rules that are excluded under these criteria.
The support of an itemset or rule measures how frequently it occurs in the data. For instance the itemset {get well card, flowers}, has support of 3 / 5 = 0.6 in the hospital gift shop data. Similarly, the support for {get well card} → {flowers} is also 0.6. The support can be calculated for any itemset or even a single item; for instance, the support for {candy bar} is 2 / 5 = 0.4, since candy bars appear in 40 percent of purchases. A function defining support for the itemset X can be defined as follows:
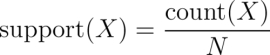
Here, N is the number of transactions in the database and count(X) is the number of transactions containing itemset X.
A rule's confidence is a measurement of its predictive power or accuracy. It is defined as the support of the itemset containing both X and Y divided by the support of the itemset containing only X:
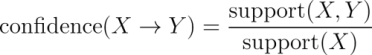
Essentially, the confidence tells us the proportion of transactions where the presence of item or itemset X results in the presence of item or itemset Y. Keep in mind that the confidence that X leads to Y is not the same as the confidence that Y leads to X. For example, the confidence of {flowers} → {get well card} is 0.6 / 0.8 = 0.75. In comparison, the confidence of {get well card} → {flowers} is 0.6 / 0.6 = 1.0. This means that a purchase involving flowers is accompanied by a purchase of a get well card 75 percent of the time, while a purchase of a get well card is associated with flowers 100 percent of the time. This information could be quite useful to the gift shop management.
Tip
You may have noticed similarities between support, confidence, and the Bayesian probability rules covered in Chapter 4, Probabilistic Learning – Classification Using Naive Bayes. In fact, support(A, B) is the same as P(A∩B) and confidence(A → B) is the same as P(B|A). It is just the context that differs.
Rules like {get well card} → {flowers} are known as strong rules, because they have both high support and confidence. One way to find more strong rules would be to examine every possible combination of the items in the gift shop, measure the support and confidence value, and report back only those rules that meet certain levels of interest. However, as noted before, this strategy is generally not feasible for anything but the smallest of datasets.
In the next section, you will see how the Apriori algorithm uses the minimum levels of support and confidence with the Apriori principle to find strong rules quickly by reducing the number of rules to a more manageable level.
Recall that the Apriori principle states that all subsets of a frequent itemset must also be frequent. In other words, if {A, B} is frequent, then {A} and {B} must both be frequent. Recall also that by definition, the support indicates how frequently an itemset appears in the data. Therefore, if we know that {A} does not meet a desired support threshold, there is no reason to consider {A, B} or any itemset containing {A}; it cannot possibly be frequent.
The Apriori algorithm uses this logic to exclude potential association rules prior to actually evaluating them. The actual process of creating rules occurs in two phases:
- Identifying all the itemsets that meet a minimum support threold.
- Creating rules from these itemsets using those meeting a minimum confidence threshold.
The first phase occurs in multiple iterations. Each successive iteration involves evaluating the support of a set of increasingly large itemsets. For instance, iteration 1 involves evaluating the set of 1-item itemsets (1-itemsets), iteration 2 evaluates 2-itemsets, and so on. The result of each iteration i is a set of all the i-itemsets that meet the minimum support threshold.
All the itemsets from iteration i are combined in order to generate candidate itemsets for the evaluation in iteration i + 1. But the Apriori principle can eliminate some of them even before the next round begins. If {A}, {B}, and {C} are frequent in iteration 1 while {D} is not frequent, iteration 2 will consider only {A, B}, {A, C}, and {B, C}. Thus, the algorithm needs to evaluate only three itemsets rather than the six that would have been evaluated if the sets containing D had not been eliminated a priori.
Continuing with this thought, suppose during iteration 2, it is discovered that {A, B} and {B, C} are frequent, but {A, C} is not. Although iteration 3 would normally begin by evaluating the support for {A, B, C}, it is not mandatory that this step should occur at all. Why not? The Apriori principle states that {A, B, C} cannot possibly be frequent, since the subset {A, C} is not. Therefore, having generated no new itemsets in iteration 3, the algorithm may stop.
At this point, the second phase of the Apriori algorithm may begin. Given the set of frequent itemsets, association rules are generated from all possible subsets. For instance, {A, B} would result in candidate rules for {A} → {B} and {B} → {A}. These are evaluated against a minimum confidence threshold, and any rule that does not meet the desired confidence level is eliminated.
