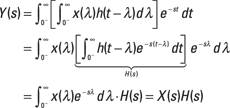Chapter 13
The Laplace Transform for Continuous-Time
In This Chapter
![]() Checking out the two-sided and one-sided Laplace transforms
Checking out the two-sided and one-sided Laplace transforms
![]() Getting to know the Laplace transform properties
Getting to know the Laplace transform properties
![]() Inversing the Laplace transform
Inversing the Laplace transform
![]() Understanding the system function
Understanding the system function
The Laplace transform (LT) is a generalization of the Fourier transform (FT) and has a lot of nice features. For starters, the LT exists for a wider class of signals than FT. But the LT really shines when it’s used to solve linear constant coefficient (LCC) differential equations (see Chapter 7) because it enables you to get the total solution (forced and transient) for LCC differential equations and manage nonzero initial conditions automatically with algebraic manipulation alone.
Returning from the s-domain requires an inverse LT procedure. In this chapter, I describe the two forms of the Laplace transform. I also tell you how to apply the Laplace transform by using partial fraction expansion and table lookup. Check out Chapter 2 for a math refresher if you think you need it.
Seeing Double: The Two-Sided Laplace Transform
Signals and systems use two forms of the Laplace transform (LT): the two-sided and the more specific one-sided. In this section, I introduce the basics of the two-sided form before diving into its one-sided counterpart.
The two-sided LT takes the continuous-time signal x(t) and turns it into the s-domain function:
![]()
where ![]() is a complex variable and the subscript in
is a complex variable and the subscript in ![]() denotes the two-sided LT.
denotes the two-sided LT.
You can find the relationship to the radian frequency FT by writing
![]()
The two-sided LT is always equivalent to the FT of signal x(t) multiplied by an exponential weighting factor ![]() . This factor allows improved convergence of the LT. If, however, the FT of
. This factor allows improved convergence of the LT. If, however, the FT of ![]() exists, it’s a simple matter to set
exists, it’s a simple matter to set ![]() in the equation and see that
in the equation and see that ![]() . This relationship is shown in Figure 13-1.
. This relationship is shown in Figure 13-1.
Finding direction with the ROC
The LT doesn’t usually converge over the entire s-plane. The region in the s-plane for which the LT converges is known as the region of convergence (ROC). Uniform convergence requires that
![]()
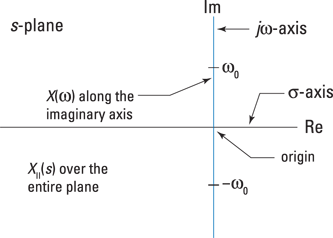
Figure 13-1: The ![]() -axis in the s-plane and the relation between
-axis in the s-plane and the relation between ![]() and
and ![]() .
.
Convergence depends only on ![]() , so if the LT converges for
, so if the LT converges for ![]() , then the ROC also contains the vertical line
, then the ROC also contains the vertical line ![]() . It can be shown that the general ROC for a two-sided signal is the vertical strip
. It can be shown that the general ROC for a two-sided signal is the vertical strip ![]() in the s-plane, as shown in Figure 13-2.
in the s-plane, as shown in Figure 13-2.
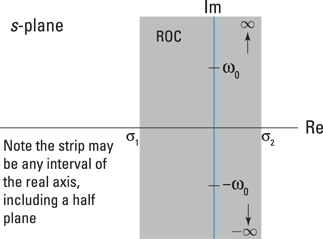
Figure 13-2: The general ROC is a vertical strip controlled by ![]() .
.
You can determine the value of ![]() and
and ![]() by the nature of the signal or impulse response being transformed. That both
by the nature of the signal or impulse response being transformed. That both ![]() and/or
and/or ![]() is also possible.
is also possible.
To show that the ROC is a vertical strip in the s-plane for x(t) two-sided, first consider x(t) is right-sided, meaning x(t) = 0 for t < t1. If the LT of x(t) includes the vertical line ![]() , it must be that
, it must be that ![]() . The ROC must also include
. The ROC must also include ![]() because the integral
because the integral ![]()
![]() is finite. What makes this true is the fact that
is finite. What makes this true is the fact that ![]() for t > 0 and t1 finite. You can generalize this result for
for t > 0 and t1 finite. You can generalize this result for ![]() to say for x(t) right-sided, the ROC is the half-plane
to say for x(t) right-sided, the ROC is the half-plane ![]() .
.
If x(t) is left-sided, meaning x(t) = 0 for t > t2 and the LT of x(t) includes the vertical line ![]() , you can show, through an argument similar to the right-sided case, that the ROC is the half-plane
, you can show, through an argument similar to the right-sided case, that the ROC is the half-plane ![]() .
.
Finally, for x(t) two-sided, the ROC is the intersection of right and left half-planes, which is the vertical strip ![]() , provided that
, provided that ![]() ; otherwise, the ROC is empty, meaning the LT isn’t absolutely convergent anywhere.
; otherwise, the ROC is empty, meaning the LT isn’t absolutely convergent anywhere.
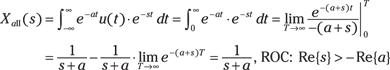
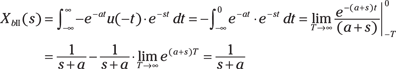
Both ![]() of Example 13-1 and
of Example 13-1 and ![]() of Example 13-2 have the same LT! The ROCs, however, are distinct — they’re complementary regions — making the LTs distinguishable only by the ROCs being different. The purpose of Example 13-2 is to point out that, without the ROC, you can’t return to the time domain without ambiguity — is the signal left-sided or right-sided?
of Example 13-2 have the same LT! The ROCs, however, are distinct — they’re complementary regions — making the LTs distinguishable only by the ROCs being different. The purpose of Example 13-2 is to point out that, without the ROC, you can’t return to the time domain without ambiguity — is the signal left-sided or right-sided?
Locating poles and zeros
When the LT is a rational function, as in Examples 13-1 and 13-2, it takes the form ![]() , where
, where ![]() and
and ![]() are each polynomials in s. The roots of
are each polynomials in s. The roots of ![]() — where
— where ![]() — are the zeros of
— are the zeros of ![]() , and the roots of
, and the roots of ![]() are the poles of
are the poles of ![]() .
.
Think of the poles and zeros as the magnitude ![]() of a 3D stretchy surface placed over the s-plane. The surface height ranges from zero to infinity. At the zero locations, because N(s) = 0, the surface is literally tacked down to zero. At the pole locations, because D(s) = 0, you have
of a 3D stretchy surface placed over the s-plane. The surface height ranges from zero to infinity. At the zero locations, because N(s) = 0, the surface is literally tacked down to zero. At the pole locations, because D(s) = 0, you have ![]() , which you can view as a tent pole pushing the stretchy surface up to infinity. It’s not your average circus tent or camping tent, but when I plot the poles and zeros in the s-plane, I use the symbols
, which you can view as a tent pole pushing the stretchy surface up to infinity. It’s not your average circus tent or camping tent, but when I plot the poles and zeros in the s-plane, I use the symbols ![]() and O.
and O.
Take a look at the pole-zero plots of ![]() and
and ![]() , including the ROC, in Figure 13-3.
, including the ROC, in Figure 13-3.
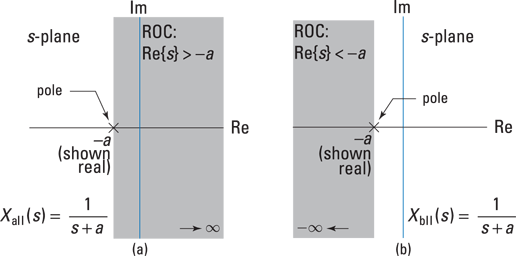
Figure 13-3: The pole-zero plot and ROC of ![]() (a) and
(a) and ![]() (b) of Examples 13-1 and 13-2, respectively.
(b) of Examples 13-1 and 13-2, respectively.
Checking stability for LTI systems with the ROC
An LTI system is bounded-input bounded-output (BIBO) stable (see Chapter 5) if ![]() .
.
Transforming to the s-domain has its perks. Here’s what I mean: The LT of the impulse response is called the system function. The Fourier transform of the impulse response is the frequency response (covered in Chapter 9), and the system function generalizes this result to the entire s-plane. The frequency domain is just the Laplace domain evaluated along the ![]() axis. It can be shown that if the ROC of
axis. It can be shown that if the ROC of ![]() contains the
contains the ![]() -axis, then the system is BIBO stable. Cool, right?
-axis, then the system is BIBO stable. Cool, right?
![]()
The triangle inequality reveals that the magnitude of a sum is bounded by the sum of the magnitudes.
Checking stability of causal systems through pole positions
The poles of ![]() must sit outside the ROC because the poles of
must sit outside the ROC because the poles of ![]() are singularities. In other words,
are singularities. In other words, ![]() is unbounded at the poles. For right-sided (and causal) systems, the ROC is the region to the right of the vertical line passing through the pole with the largest real part. In Example 13-1, this represents all the values greater than
is unbounded at the poles. For right-sided (and causal) systems, the ROC is the region to the right of the vertical line passing through the pole with the largest real part. In Example 13-1, this represents all the values greater than ![]() .
.
Digging into the One-Sided Laplace Transform
The one-sided Laplace transform (LT) offers the capability to analyze causal systems with nonzero initial conditions and inputs applied, starting at ![]() . Unlike two-sided LT signals, the one-sided LT doesn’t allow you to analyze signals that are nonzero for
. Unlike two-sided LT signals, the one-sided LT doesn’t allow you to analyze signals that are nonzero for ![]() . The trade-off is acceptable because the transient analysis of causal LTI systems in the s-domain involves only algebraic manipulations.
. The trade-off is acceptable because the transient analysis of causal LTI systems in the s-domain involves only algebraic manipulations.
The one-sided LT restricts the integration interval to ![]() :
:
![]()
Use the ![]() to accommodate signals such as the impulse
to accommodate signals such as the impulse ![]() and the step
and the step ![]() (see Chapter 5). To be clear,
(see Chapter 5). To be clear, ![]() is
is ![]() as
as ![]() approaches zero.
approaches zero.
All the results developed for the two-sided LT in the previous section hold under the one-sided case as long as the signals and systems are causal — that is, both ![]() and
and ![]() are zero for
are zero for ![]() . The poles of
. The poles of ![]() must lie in the left-half plane for stability.
must lie in the left-half plane for stability.
![]()
The ROC is ![]() . In terms of
. In terms of ![]() , the ROC is just
, the ROC is just ![]() . This means that the ROC includes the entire s-plane. And when
. This means that the ROC includes the entire s-plane. And when ![]() , the
, the ![]() is needed to properly handle the integral of
is needed to properly handle the integral of ![]() .
.
Use Example 13-1 and set ![]() :
:
![]()
The ROC doesn’t include the ![]() -axis because a pole is at zero.
-axis because a pole is at zero.
Again, use Example 13-1, where two-sided and one-sided signals are identical:
![]()
One zero and two poles exist in this solution: ![]() . You can find the ROC for the solution as a whole by intersecting the ROC for each exponential term. Just use the ROC from Example 13-1:
. You can find the ROC for the solution as a whole by intersecting the ROC for each exponential term. Just use the ROC from Example 13-1: ![]()
The pole with the largest real part sets the ROC boundary. The system is stable because the ROC includes the ![]() -axis. But a more memorable finding is the fact that the poles are in the left-half s-plane, which indicates that this causal system is stable.
-axis. But a more memorable finding is the fact that the poles are in the left-half s-plane, which indicates that this causal system is stable.
Checking Out LT Properties
Problem solving with the LT centers on the use of transform theorems and a reasonable catalog of transform pairs. Knowing key theorems and pairs can help you move quickly through problems, especially when you need an inverse transform. In this section, I point out some of the most common LT theorems and transform pairs.
Transform theorems
In this section of basic theorems, assume that the signals and systems of interest are causal.
Find a collection of significant one-sided Laplace transform theorems in Figure 13-4.
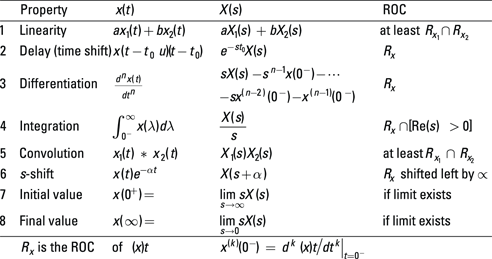
Figure 13-4: One-sided Laplace transform theorems.
Delay
The one-sided LT of a signal with time delay t0 > 0 is an important modeling capability. To set up the theorem, consider ![]() for
for ![]() :
:
![]()
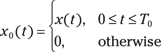
To find ![]() , write
, write ![]() .
.
Taking the LT of both sides results in the following equation:
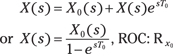
Differentiation
The differentiation theorem is fundamental in the solution of LCC differential equations with nonzero initial conditions. If you start with ![]() , you ultimately get a result for
, you ultimately get a result for ![]() . Using integration by parts, you can show that
. Using integration by parts, you can show that
![]()
Using mathematical induction, you can then show the following, where ![]() :
:
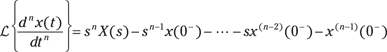
Integration
The integration theorem is the complement to the differentiation theorem. It can be shown that
![]()
![]()
This is a repeated pole at s = 0 with the ROC the right-half plane.
Convolution
Given causal ![]() , the convolution theorem states that
, the convolution theorem states that ![]()
![]() . This theorem is fundamental to signals and systems modeling, because it allows you to study the action of passing a signal through a system in the s-domain. An even bigger deal is that convolution in the time domain is multiplication in the s-domain. The FT convolution theorem (see Chapter 9) provides this capability, too, but the LT version is superior, especially when your goal is to find a time-domain solution.
. This theorem is fundamental to signals and systems modeling, because it allows you to study the action of passing a signal through a system in the s-domain. An even bigger deal is that convolution in the time domain is multiplication in the s-domain. The FT convolution theorem (see Chapter 9) provides this capability, too, but the LT version is superior, especially when your goal is to find a time-domain solution.
s-shift
Solving LCC differential equations frequently involves signals with an exponential decay. The s-shift theorem provides this information:
![]()
The s-shift moves all the poles and zeros of ![]() to the left by
to the left by ![]() . The left edge of the ROC also shifts to the left by
. The left edge of the ROC also shifts to the left by ![]() . Stability improves!
. Stability improves!
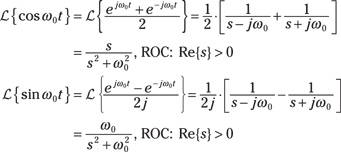
Finally, let ![]() :
:
![]()
The poles that were at ![]() shift to
shift to ![]() . The ROC for both transforms is
. The ROC for both transforms is ![]() .
.
Final value
The final value theorem states that ![]() if the limit exists — or x(t) reaches a bounded value only if the poles of
if the limit exists — or x(t) reaches a bounded value only if the poles of ![]() lie in the left-half plane (LHP). This theorem is particularly useful for determining steady-state error in control systems (covered in Chapter 18). You don’t need a complete inverse LT just to get
lie in the left-half plane (LHP). This theorem is particularly useful for determining steady-state error in control systems (covered in Chapter 18). You don’t need a complete inverse LT just to get ![]() .
.

What’s wrong with the analysis of ![]() ? Poles on the
? Poles on the ![]() -axis (
-axis (![]() ) make
) make ![]() oscillate forever. The limit doesn’t exist because the poles of
oscillate forever. The limit doesn’t exist because the poles of ![]() don’t lie in the LHP, so the theorem can’t be applied. The moral of this story is to study the problem to be sure the theorem applies!
don’t lie in the LHP, so the theorem can’t be applied. The moral of this story is to study the problem to be sure the theorem applies!
Transform pairs
Transform pairs play a starring role in LT action. After you see the transform for a few signal types, you can use that result the next time you encounter it in a problem. This approach holds for both forward and inverse transforms (see the section “Getting Back to the Time Domain,” later in this chapter). Figure 13-5 highlights some LT pairs.
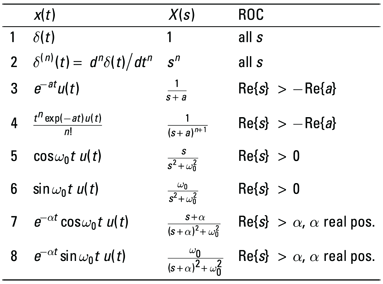
Figure 13-5: Laplace transform pairs.
The starting point from the s-domain side is ![]() , with
, with ![]() to ensure complex conjugate poles. You can write the time-domain solution as a linear combination of the time-domain side of transform pairs in Lines 7 and 8 of Figure 13-5:
to ensure complex conjugate poles. You can write the time-domain solution as a linear combination of the time-domain side of transform pairs in Lines 7 and 8 of Figure 13-5: ![]() . Your objective is to find a and b in terms of the coefficients of X(s). You can do so with the following steps:
. Your objective is to find a and b in terms of the coefficients of X(s). You can do so with the following steps:
1. Equate X(s) with a linear combination of the s-domain side of transform pairs in Lines 7 and 8 of Figure 13-5 by first matching up the denominators in
![]()
Recall the old algebra trick called completing the square, in which, given a quadratic polynomial ![]() , you rewrite it as
, you rewrite it as ![]() , where c1 and c2 are constants. You then equate like terms:
, where c1 and c2 are constants. You then equate like terms:
![]()
So ![]() and
and ![]() or
or ![]() .
.
2. Find a and b by matching like terms in the numerator: ![]() and
and ![]() or
or ![]() .
.
As a test case, consider ![]() . Using the equations for
. Using the equations for ![]() , a, and b in Steps 1 and 2, you find that
, a, and b in Steps 1 and 2, you find that ![]() , a = 1, and
, a = 1, and ![]() ; for example:
; for example:
![]()
On the time-domain side, you have
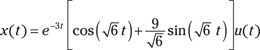
To check this with Maxima you use the ILT function ilt() and find agreement when using the original X(s) function:
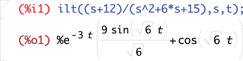
Getting Back to the Time Domain
Working in the s-domain is more of a means to an end than an end itself. In particular, you may bring signals to the s-domain by using the LT and then performing some operations and/or getting an s-domain function; but in the end, you need to work with the corresponding time-domain signal.
Returning to the time domain requires the inverse Laplace transform (ILT). Formally, the ILT requires contour integration, which is a line integral over a closed path in the s-plane. This approach relies on a complex variable theory background.
In this section, I describe how to achieve contour integration by using partial fraction expansion (PFE) and table lookup. I also point out a few PFE considerations and include examples that describe how these considerations play out in the real world.
The general formula you need to complete the ILT is
![]()
The first step is to ensure that ![]() is proper rational, that
is proper rational, that ![]() . If it isn’t, you need to use long division to reduce the order of the denominator. After long division, you end up with this:
. If it isn’t, you need to use long division to reduce the order of the denominator. After long division, you end up with this:
![]()
![]() is the remainder, having polynomial degree less than N.
is the remainder, having polynomial degree less than N.
Dealing with distinct poles
If the poles are simple (unrepeated) and ![]() is proper rational, you can write
is proper rational, you can write ![]() , where the
, where the ![]() represents the nonzero poles of
represents the nonzero poles of ![]() . Find the PFE coefficients by using the residue formula:
. Find the PFE coefficients by using the residue formula: ![]() (see Chapter 2).
(see Chapter 2).
If you need to perform long division (such as when the order of the numerator polynomial is greater than or equal to the order of the denominator polynomial), be sure to augment your final solution with the long division terms ![]() .
.
Working double time with twin poles
When ![]() has the pole
has the pole ![]() repeated once (a multiplicity of two), the expansion form is augmented as follows:
repeated once (a multiplicity of two), the expansion form is augmented as follows:
![]()
You can find the coefficients ![]() by using the residue formula. The formula for
by using the residue formula. The formula for ![]()
is ![]() and
and ![]() is found last by substitution. See Example 13-11.
is found last by substitution. See Example 13-11.
Completing inversion
For the general ILT scenario outlined at the start of the section, invert three transform types via table lookup. The first manages the long division result; the second, distinct poles; and the third, poles of multiplicity two:
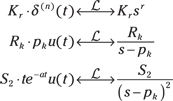
Using tables to complete the inverse Laplace transform
This section contains two ILT examples that describe how to complete PFE with the table-lookup approach. The first example, Example 13-11, considers a repeated real pole; the second, Example 13-12, considers a complex conjugate pole pair. Both examples follow this step-by-step process:
1. Find out whether X(s) is a proper rational function; if not, perform long division to make it so.
2. Find the roots of the denominator polynomial and make note of any repeated poles (roots) and/or complex conjugate poles (roots).
3. Write the general PFE of X(s) in terms of undetermined coefficients.
For the case of complex conjugate pole pairs, use the special transform pair developed in Example 13-9 so the resulting time domain is conveniently expressed in terms of exponentially damped cosine and sine functions.
4. Solve for the coefficients by using a combination of the residue formula and substitution techniques as needed.
5. Apply the ILT to the individual PFE terms, using table lookup.
6. Check your solution by using a computer tool, such as Maxima or Python.
1. Use the repeated roots form for PFE to expand H(s) into three terms:
![]()
2. Find the coefficients R1 and S2, using the residue formula as described in section “Working double time with twin poles”:
![]()
3. Solve for ![]() by direct substitution. Let
by direct substitution. Let ![]() :
:
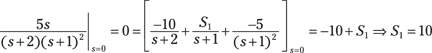
4. Place the values you found for R1, S1, and S2 into the expanded form for H(s) of Step 1, and then apply the ILT term by term:
![]()
Check the results with Maxima to see that all is well:
![]()
![]()
All the poles are distinct, so you can use the residue formula to find the PFE coefficients and the impulse response. This approach results in real and complex exponential time-domain terms — not a clean solution without further algebraic manipulation. But the impulse response is real because all the poles are either real or complex conjugate pairs, so the complex exponentials do reduce to real sine and cosine terms.
For this scenario, I recommend using the s-shift theorem and the associated transform pairs found in the earlier section “s-shift,” because this approach takes you to a usable time-domain solution involving damped sine and cosine terms. Example 13-10 boiled all of this down to a nice set of coefficient equations. The PFE expansion for the conjugate pole term is ![]() . You can find the equations for
. You can find the equations for ![]() , a, and b in Example 13-10.
, a, and b in Example 13-10.
Now it’s time for action. Here’s the process:
1. For the three-pole system, complete the square of the complex conjugate pole term.
Use the equations from Step 1 of Example 13-10, noting that, here, a1 = 2 and a0 = 2: ![]() and
and ![]() . Write the PFE as
. Write the PFE as
![]()
2. Solve for ![]() by using the residue formula; then use variable substitution to find a and b.
by using the residue formula; then use variable substitution to find a and b.
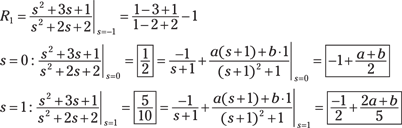
3. Solve the two equations for the unknowns to find ![]() .
.
Use the transform pairs Lines 3, 7, and 8 in Figure 13-5 to get the inverse transform of the three terms:
![]()
Checking with Maxima shows agreement:
![]()
Working with the System Function
The general LCC differential equation (see Chapter 7) is defined as
![]()
By taking the LT of both sides of this equation, using linearity and the differentiation theorem (described in the section “Transform theorems,” earlier in this chapter), you can find the system function ![]() as the ratio of
as the ratio of ![]() .
.
![]()
This works because of the convolution theorem (see Figure 13-4), ![]() or
or ![]() .
.
Assuming zero initial conditions, you use the differentiation theorem (see Figure 13-4) to find the LT of each term on the left and right sides of the general LCC differential equation. You then factor out Y(s) and X(s) and form the ratio Y(s)/X(s) = H(s) on the left side, and what remains on the right side is the system function:
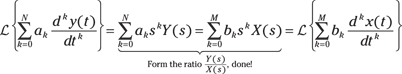
After you solve for ![]() , you can perform analysis of the system function alone or in combination with signals.
, you can perform analysis of the system function alone or in combination with signals.
![]() Plot the poles and zeros of H(s) and see whether the poles are in the left-half plane, making the system stable.
Plot the poles and zeros of H(s) and see whether the poles are in the left-half plane, making the system stable.
![]() Assuming the system is stable, plot the frequency response magnitude and phase by letting
Assuming the system is stable, plot the frequency response magnitude and phase by letting ![]() in H(s) to characterize the system filtering properties.
in H(s) to characterize the system filtering properties.
![]() Find the inverse LT
Find the inverse LT ![]() to get the impulse response,
to get the impulse response, ![]() — the core time-domain characterization of the system.
— the core time-domain characterization of the system.
![]() Find the inverse LT
Find the inverse LT ![]() to get the step response.
to get the step response.
![]() Find the inverse LT
Find the inverse LT ![]() to get the output
to get the output ![]() in response to a specific input
in response to a specific input ![]() .
.
Managing nonzero initial conditions
A feature of the one-sided LT is that you can handle nonzero initial conditions when solving the general LCC differential equation. The key to this is the differentiation theorem. The lead term snX(s) is the core result of the theorem, but the nonzero initial conditions are carried by the terms ![]() , k = 0, … , n – 1.
, k = 0, … , n – 1.
1. Apply the differentiation theorem (see Figure 13-4) to both sides of the LCC differential equation:
![]()
2. Solve for ![]() , making substitutions for
, making substitutions for ![]() and
and ![]() :
:
![]()
Use Line 3 of Figure 13-5: ![]() .
.
3. Solve for the partial fraction coefficients R1 and R2:
![]()
4. Insert the coefficients into the PFE for Y(s) and then apply the inverse Laplace transform to each term:
![]()
Check Maxima to see whether it agrees:
![]()
Checking the frequency response with pole-zero location
The location of the poles and zeros of a system controls the frequency response ![]() —
— ![]() . Consider the following:
. Consider the following:
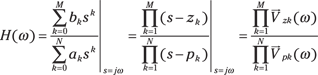
pk and zk are the poles and zeros of H(s) and ![]() and
and ![]() are the frequency response contributions of each pole and zero. The vectors
are the frequency response contributions of each pole and zero. The vectors ![]() point from the zero and pole locations to
point from the zero and pole locations to ![]() on the imaginary axis. This provides a connection between the pole-zero geometry and the frequency response. In particular, the ratio of vector magnitudes,
on the imaginary axis. This provides a connection between the pole-zero geometry and the frequency response. In particular, the ratio of vector magnitudes, ![]() , is the magnitude response. The phase response is
, is the magnitude response. The phase response is ![]() .
.
![]()
The single numerator and denominator vectors indicates that the geometry is rather simple. You can use the software app PZ_Geom_S to further explore the relationship between frequency response and pole-zero location. Check out the screen shot of PZ_geom_S in Figure 13-6.
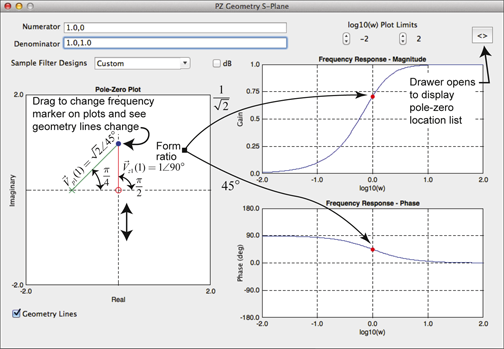
Figure 13-6: The app PZ-Geom_S displaying the pole-zero geometry for ![]()
![]() .
.

 Unlike the frequency domain, which has real frequency variable
Unlike the frequency domain, which has real frequency variable  It’s no accident that I chose
It’s no accident that I chose  Example 13-1: Find the two-sided LT of the right-sided signal
Example 13-1: Find the two-sided LT of the right-sided signal  The proof follows by expanding
The proof follows by expanding  The theorems and transform pairs developed in this section are valid for the one-sided LT. Those applicable to the two-sided LT are different in some cases.
The theorems and transform pairs developed in this section are valid for the one-sided LT. Those applicable to the two-sided LT are different in some cases.