Solutions to Problems

Chapter 2

Solution to Problem 2.1

(a) What is the shape and magnitude of the amplifier output voltage V₀?

Figure 1(a) shows an equivalent circuit diagram of the front-end amplifier, including the cable capacitances, where C_p1 = C_p2 = 100 pF. Capacitor C_p1 charges the excitation voltage source. However, because of the low impedance (zero ohm), this has no effect on the voltage across the sensor capacitor C_s. With respect to C_p2 it can be noted that, with an ideal amplifier, the amplifier input voltage equals 0 V. Because this voltage equals the voltage over C_p2, the current through C_p2 equals zero. Therefore, the current I_i (Figure 1(a)) equals

where s represents the Laplace operator. The output voltage V₀ equals

Equation (2) shows that the amplifier with its feedback circuitry has a real amplification factor, which equals C_s/C_f = 1/5. Therefore, the output voltage is a square-wave voltage with a peak-to-peak value of 2 V.

(b) What is the shape and magnitude of the amplifier output voltage V₀ for this modified circuit configuration?

Figure 1(b) shows the equivalent circuit diagram of the front-end amplifier, including the parasitic capacitor. The input voltage over the capacitors C_s and C_p2 is equal to V_exc. Therefore, the current I_i amounts to

and

Figure 1 Effect of connecting cables for capacitive sensors (a) with two-port connection; (b) with one-port connection.

In case of an ideal amplifier with an unlimited output voltage, the output voltage will have a peak-to-peak value of 212 V. In practice, however, the supply voltage will limit this voltage. In this case the amplifier is not linear any more and the gain will drop towards a low value. Note that this unfavorable situation is due to the large effect of the parasitic capacitance C_p2. Therefore, in the case of a grounded capacitive sensor, it is advised to use active guarding of the shield (see Chapter 8, Section 8.4.3).

Solution to Problem 2.2

(a) Find by calculation the magnitude of the voltage rise.

In case of an ideal amplifier, the voltage over the leakage resistor R_leak is V_exc, so that I_i = I_cs + I_leak (Figure 2(a)). The leakage current, which is added to the desired current I_cs, is integrated by the capacitor C_f and causes the output voltage rise V_rise of the output voltage, which is

or in the time domain, over half a period (t₂ − t₁):

Figure 2 (a) Electrical model of the sensing elements, (b) the output voltage V_o versus the time.

Substitution of the values depicted in Figure 2.29(b) into Equation (6) shows that V_rise = 25 mV.

(b) Calculate the relative error in this sample, as compared with the ideal value V_{o, ideal}.

In the ideal case that R_leak → ∞, the output voltage V_o(t₂) = V_{o, ideal}(t₂) equals

At the beginning of the time interval (t₂ to t₁), just after the transient, with a leakage resistor, the voltage V_o(t₁) = (V_{o, ideal}(t₂) + V_rise/2) will be somewhat higher than in the ideal case. Note that during the (very short) transient time, the leakage resistor does not affect the magnitude of the voltage step.

Therefore, at the sampling moment, the relative effect ε_sh of the shunting resistor is

Substitution of Equations (6) and (7) into Equation (8) yields:

Note that even with such a high shunting-resistor value, there is already a significant effect!

Solution to Problem 2.3

Calculate the relative error ΔV_ch/V_ch of the voltage samples.

The voltage V_ch across the capacitor C_p rises exponentially from 0 V to V_s, according to the equation

At t = t₂ for the voltage difference ΔV_ch it holds that

with τ = R_sC_{p =}1 μs.

With t₂ − t₁ = 10 μs, which is the time interval of half a period, it holds that (t₂ − t₁)/τ = 10, so that

Solution to Problem 2.4

Why do we need the z resistors at the amplifier output?

These resistors are needed to eliminate the influence of the series resistance on the switches. In the resistive feedback network of Figure 3 (≡Figure 2.13), no switches are used in the resistor chain. All of them are outside the chain. In the circuit shown in Figure 3, the ON resistances of the switches S₁, S₂, S₅ and S₆ do not affect the output voltage, because no current is flowing through them. Through the switches S₃ and S₄ significant currents do flow, which cause a voltage drop over these switches. However, this voltage drop does not affect the sensed output voltage Vout.

Solution to Problem 2.5

Why do we need the switch S₃ ?

Suppose we were to remove switch S₃, then the dc biasing conditions for the amplifier would be violated. The dc output voltage of the amplifier would no longer be defined, and would drift away according to any leakage current I_leak at the inverting amplifier input terminal. Such a leakage current would be integrated over the capacitor C_f, causing the output voltage drift. Over a time interval T, this drift would be equal to I_leakT/C_f. At one point the output voltage (which is limited by the supply voltage) would drift beyond the linear region of the amplifier, so that the amplifier gain would drop towards a low value. Closing the reset switch S₃ will bring the output voltage back to a safe value of V_o = 0 V. As soon as the switch is opened again, the drift process restarts, so that another reset is needed before the output voltage reaches a critical value.

Figure 3 The principle of a dynamic-feedback instrumentation amplifier, as shown in Figure 2.13.

Figure 4 The effect of a leakage current I_leak at the inverting input terminal of the amplifier.

Chapter 4

Solution to Problem 4.1

Assume a power density of the incident light P [W/m²]. The photocurrent density can be calculated using both the responsivity and the external quantum efficiency. Equating the expressions results in the relation between R and η.

Firstly, the calculation based on the responsivity yields a current density J = R × P. Secondly, the calculation based on quantum efficiency makes use of the relation between the photon flux (i.e. the number of photons that pass a unit cross-sectional area per unit time), Φ_ph [photons/m²s], and the power density of the incident radiation: Φ_ph = P/E_ph, [W/m²]/[J = Ws], where E_ph denotes the energy per photon: E_ph = h_pc/λ. Hence Φ_ph = Pλ/(h_pc). The external quantum efficiency describes the efficiency of the opto-electrical conversion in terms of the number of electrons generated per incident photon: Φ_e = ηΦ_ph = ηPλ/ (h_pc). The current density follows as: J = qΦ_e = qηλ/(h_pc).

Equating these two expressions for the photocurrent density yields: R = qηλ/(h_pc). Substitution of η = 0.8 for λ = 500 nm yields: R = 0.32 A/W.

Solution to Problem 4.2

Refer to Figure 4.11. Material figure-of-merit: μ_nτ_n = 0.15 m²V⁻¹s⁻¹ × 2.5 × 10⁻³s = 3.75 × 10⁻⁴ m²/V. W/L-ratio: L = feature size = 10 μm. W = (2n−1)w_f, with n as the number of finger pairs in the meander and w_f as the length of a finger. Inspection of the 1000 × 1000 μm² detector area shows that w_f = 1000 μm − 2 × 20 μm = 960 μm and n = 1000 μm/(4 × 10 μm) = 25. Hence, W/L = 4704 and yields Δ σ/q Φ _to = (μ_nτ_n) (W/L) = 1.76 m²/V.

The photoconductive gain is expressed in Equation (4.15):

Note that the range of excitation voltages is very limited. V_exc=3 V would yield a breakdown field. Cut-off frequency f_c = (2πτ_n)⁻¹ = 64 Hz.

Solution to Problem 4.3

Equation (4.16), detector only: NEP = (1.6 × 10⁻³⁰ A²/Hz × 100 Hz)^1/2/0.3 A/W = 42.2 × 10⁻¹⁵ W.

Equation (4.46), detector plus readout: NEP = [(1.6 × 10⁻³⁰ A²/Hz + 10⁻²⁵ A²/Hz) × 100Hz]^1/2/0.3 A/W = 10.5 × 10⁻¹¹ W.

Equation (4.47), detector: D^∗ = 0.3 A/W (10⁻² cm²/1.6 × 10⁻³⁰ A²/Hz × 100 Hz)^1/2 = 2.37 × 10¹² cm Hz^1/2/W).

Equation (4.47) system: D^∗ = 0.3 A/W (10⁻² cm²/(1.6 × 10⁻³⁰ A²/Hz + 10⁻²⁵ A²/Hz) × 100 Hz)^1/2 = 9.5 × 10⁷ cm Hz^1/2/W).

P_s = 10⁻³ × 10⁻⁶ = 10⁻¹⁰ W

Hence, SNR_detector = 2370 = 33.7 dB. However, SNR_system = −0.21 dB. The signal is below noise level. Note that dc detection is usually offset limited.

Chapter 6

Solution to Problem 6.1: square thermopile design

The sensitivity of the thermopile is given by the Seebeck coefficient of each thermocouple times the number of couples. The Seebeck coefficient of a couple is determined by the difference in coefficient of both strips. The p-type silicon has a coefficient of +0.15 mV/K, and the n-type of −0.15 mV/K, so the difference is 0.30 mV/K. The number of strips of the thermopile can be calculated using Equation (6.30) to be 10. This gives 10 strips of 1.5 mm in length and 0.15 mm in width, each having a resistance of 750 Ω (so it is justified to neglect the required separation between strips, which is of the order of a few μm). The sensitivity of the thermopile is 10 × 0.30 mV/K = 3 mV/K.

Solution to Problem 6.2: forced convection

What is the heat transfer?

For this we use Equation (6.10). First we calculate the Reynolds number (Re = UL/ν), with L = 1.5 mm, U = 1 m/s and ν = 15 × 10⁻⁶ m²/s, we find Re = 100, and for such small Reynolds number the flow is indeed laminar. With the Prandtl number of 0.7 we find the convective heat transfer G_conv ≈ 5.9 κ/L. With the thermal conductivity of air of 25 mW/K m, this gives G″_conv ≈ 100 W/K m². For the area of 1.5 mm × 1.5 mm and a temperature difference of 5 K the total heat transfer amounts to 1.125 mW.

Solution to Problem 6.3: measurement of flow direction

(1) Calculate the output voltage of the thermopile.

This is given by the temperature difference across the thermopile times the thermopile sensitivity. The temperature difference is given by the differential heat flow times the thermal resistance of the silicon slab through which the heat flows. We assumed that all the heat flows over a distance of 0.75 mm. The thermal resistance of that slab of silicon, 0.75 mm long, 1.5 mm wide and 0.1 mm thick, is approximately 0.5 Square × thermal sheet resistance = 0.5 × (1/κD) = 0.5 × 67 K/W = 33 K/W. The net heat flowing through this resistance is (0.71−0.29) × 1.125 mW = 472 μW. This creates a temperature difference across the thermal resistance of 33 K/W of 15.6 mK. The sensitivity of the thermopile is Nα_s = 3 mV/K. Thus, the output signal of the thermopile will be 47 μV.

(2) How is the sign of the output voltage related to the flow?

The strongest cooling occurs at the upstream edge, so the upstream edge will be the coldest. If the flow reverses, the edge called upstream becomes the edge called downstream and vice versa, and the temperatures will also change accordingly. So, the sign of the output voltage is directly related to the direction of the flow. Whether the sign of the output voltage is positive or negative in the one direction trivially depends upon the actual connection to the outside.

Solution to Problem 6.4: the influence of micromachining

What is the first estimate for the output voltage of the thermopile now?

In a first estimate we assume that the differential heat flow has the same value as in Problem 6.3: 472 μW. The sensitivity of the thermopile is again 3 mV/K. The only change lies in the thermal resistance of the slab silicon in which the thermopile is integrated. This silicon slab is now 25 times thinner than the wafer-thick sensor. So, the thermal resistance is 25 times as high, or 833 K/W. The temperature difference will be 472 μW × 833 K/W = 0.39 K. With a thermopile sensitivity of 3 mV/K, the output voltage would be 1.17 mV. Because 0.39 K is significant as compared to the sensor temperature elevation of 5 K, the heat transfer and the temperature distribution in the membrane will influence each other, so the solution is an approximation only.

Solution to Problem 6.5: infrared radiation

(1) What is the net power exchange between sensor and object?

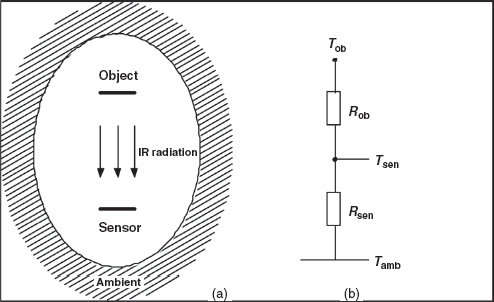
For this we use Equation (6.12), and we find (with ε = 1, A_obj/d² = (1/56)² and A_D = 2 × 10⁻⁶ mm²) that P_ir = 12.5 nW. In electrical network terms (Figure 5) it is ΔTR_sen/ (R_sen + R_ob) = ΔTG_ob/(G_ob + G_sen).

(2) What is the temperature increase of the floating membrane of the sensor, if its thermal conductance to the ambient is 330 μW/K?

This is simply 12.5 nW/(330 μW/K) = 38 μK.

(3) Make an estimate of the three major components making up the thermal conductance from the floating membrane to the ambient if the sensor is encapsulated in nitrogen, κ_N = 2 mW/K m?

Figure 5 (a) Infrared sensor viewing an object and (b) its equivalent electrical model.

The thermal conductance to the ambient is composed of heat transfer by infrared radiation, by conductance through the nitrogen, and by conductance through the suspension beam(s).

Firstly, let us approximate the heat transferred by infrared radiation from the floating membrane to the ambient. From Equation (6.11), we have that infrared heat transfer will be G^″_rad = 6 W/K m², where we should take the surface of the floating membrane twice, since it will be emitting radiation to above and to below the membrane. So, this will give a thermal conduction by radiation of 24 μW/K. In total, the thermal conduction to the ambient is 330 μW/K, so 306 μW/K is transferred by conduction through suspension beams and gas conduction.

Secondly, let us estimate the thermal conduction by the gas in the gap under the floating membrane, which is typically 500 μm (being a standard 4 inch wafer thickness; note that surface micromachining in this case would give a very bad performance). For an area of 2 mm², and with the thermal conductivity of nitrogen being 26 mW/K m, this conduction will be of the order of 100 μW/K. Let us double this to account for conduction on the sides and to the top of the sensor housing.

Finally, this leaves about 100 μW/K for the conduction through the suspension beams, which corresponds to a thermal resistance of 10 kK/W. For beams with a thickness of 4 μm, that have a thermal sheet resistance of 1.67 kK/W, each of the beams will have a length of 12 squares. Assuming that they run over the full length along the floating membrane, their dimensions would be 2 mm long and 160 μm wide.

(4) Estimate the improvement if the sensor were encapsulated in xenon (κ_Xe = 6 mW/K m) instead of in nitrogen?

By using xenon around the sensor, whose heat conduction is about one-fifth of that of nitrogen, the thermal conductance through the gas is reduced to about 45 μW/K, and this causes the overall thermal conductance to the ambient to be approximately halved. Therefore, the sensitivity of the device is doubled.

Solution to Problem 6.6: thermal modeling

(1) What is the beam's thermal resistance compared to that of the floating membrane?

The thermal sheet resistance of the beam is R_st = 1/(κD) = 1333 K/W (see Section 6.3.3). Its overall resistance, without the conductance of the argon, is 10 squares times the sheet resistance, 13 kK/W, or a conductance of 75 W/K. According to the Equation (6.23), there will be a loss in resistance due to the conductance by the argon. First, we will calculate the transmission-line constant γ for low frequencies, according to Equation (6.21). For this we must know G″_p, which can be found using Equation (6.9), with distance d = 0.5 mm, and κ = 18 mW/K m, and multiplying by two to account for the upper and lower surface of the beam. With these values we find that G^″ = 72 W/K m² and γ = 310/m. Moreover, we find that (γL)²/3 = 0.13, so the effective thermal resistance of the beam becomes 11.6 kK/W. For the floating membrane, we find a thermal conductance to the ambient G_flm equal to G^″ × 2 mm² = 144 μW/K, or a resistance of 7 kK/W. The thermal resistance of the beam is, therefore, twice the thermal resistance between the floating membrane and the ambient through gas conduction.

(2) How do the thermal time constants of the beam and the overall system compare?

The thermal time constant of the beam follows from Equation (6.24) and, with a thermal square-meter heat capacity C_th = 1.6 MJ/m³ K × 5 μm = 8 J/m² K, yields a time constant of 14 ms. For the floating membrane, the overall thermal resistance is 4.3 kK/W and the thermal capacitance is 2 mm² × 8 J/K m² = 16 μJ/K, the product of which gives the time constant of 69 ms. So, the time constant of the beam can be neglected.

Solution to Problem 6.7: circular thermopiles

What is the sensitivity of the thermopile?

For this we make an estimation of the electrical resistance R_tp of the thermopile by using the equation given for the thermal resistance of a closed membrane, Equation (6.15). The analogy between electrical and thermal models is a two-way street and those familiar with thermal problems can use the solutions to evaluate electrical problems as well. In Equation (6.15) we use the electrical sheet resistance R_se instead of the thermal sheet resistance R_st. We find that for a thermopile consisting of a single strip of 360°, the electrical resistance becomes R_se ln(r_in/r_out)/2π = 5.5 Ω. Note that the electrical resistance of the thermopile increases with the square of the number of strips, as indicated by Equation (6.32). This holds also true for the case that we divide the full circle into arcs. A resistance of 80 kΩ is allowed, so we can afford (80 kΩ/5.5 Ω)^1/2 = 120 strips. These strips will be, at the inner radius, 47 μm wide including the (neglected) separation. If 5 μm separation is usually required, the strips are 10 % narrower at their narrowest end, near the center of the thermopile. In practice, the thermopile will be (5 to 10) % higher in resistance. All this gives a sensitivity of 120 × 0.6 mV/K = 72 mV/K.

Solution to Problem 6.8: chemical microcalorimeter

(1) What is the sensitivity of this microcalorimeter for glucose?

The sensitivity of the thermopile is 72 mV/K. The thermal sheet resistance of the membrane is 1/(150 W/K m × 5 μm) = 1333 K/W . With Equation (6.24) for homogeneous heating we find, with a heat generation of P^″ = 1 W/m², a membrane of 1.8 mm radius (r_rim), and a thermopile with a 0.9 mm inner radius (r), that the temperature increase will be 1.44 mK/W/m², or 1.44 mK/mmol/l. Multiplying by the thermopile sensitivity gives the overall sensitivity, which is 103 μV/mmol/l. This is a rather high value, and in practice we find sensitivities an order of magnitude lower, because of the thermal conduction and convection of the glucose solution flowing past the sensor. Values of the order of (5 to 10) μV/mmol/l are observed in practice.

(2) What is the resolution in a 1 Hz band?

For this we calculate the thermal or Johnson noise u_n, which is given by the well-known formula u_n = (4kTR_tp)^1/2 for a (0 to 1) Hz band. The electrical resistance R_tp of the thermopile is 80 kΩ, and the noise is 36 nV. If we define the resolution to be the signal where a signal-to-noise ratio of 8 exists for easy readout of the results, the electrical signal at resolution is 0.3 μV, and the resolution for glucose is 50 μmol/l, if we take a sensitivity of 6 μV/mmol/l.

Solution to Problem 6.9: self-heating in a resistor

What is the error in the temperature measurement caused by the self-heating of the resistor?

We first calculate the thermal resistance between the resistor and the rest of the chip. Assuming radial heat flow with Equation (6.16), we can find the thermal resistance. Because we are working in a half-space, this value is multiplied by a factor of 2. As the outer radius, we take infinity, as the inner radius, we take a half-sphere with the same area as the resistor surface, which is 625 μm². The inner radius is given by 2πr² = 625 μm², so r = 10 μm. This gives a thermal resistance of 106 K/W. At a dissipation of 100 μA × 100 μA × 3.9 kΩ = 39 μW, the error is 4.1 mK, quite acceptable in many cases. Note that assuming an outer radius of infinity causes a minor error. In comparison with substituting a more practical value of 0.5 mm, which is representative for the chip thickness, this error amounts to only 2 %.

Chapter 7

Solution to Problem 7.1

(1) What is the temperature rise due to self-heating?

According to Figure 7.7(b) the thermal conductance amounts to G_sg ≅ 1.1 × 10⁻³ W K⁻¹. Therefore, a continuous power dissipation P of 1 mW will cause a temperature rise of about P/G_sg = 0.9 K. Increasing the sensor area, for instance by assembling the chip on a flat ceramic substrate or by using flat connecting wires, can reduce this effect. Another excellent way to reduce this effect is explained in the part (3) of this problem.

(2) In the case of single-sided flow the cooling area is only half of what it was before. Consequently, thermal conductance will have only have half of its original value, being 0.55 × 10⁻³ W K⁻¹, which will double the temperature rise.

(3) Calculate the mean temperature rise ΔT_mean during a switch-on time of 30 ms.

As a first step we determine the thermal time constant τ. The simplest way is to use the measurement result presented in Figure 7.7(b), which shows that at the specified flow velocity of 1 m/s that τ ≅ 0.6 s. As an alternative this time constant can also been found from the calculation of τ = C_th/G_sg, where G_sg is the thermal conductance calculated in part (1) of this problem and C_th is the thermal capacitance which equals the product of the chip volume and the specific heat. For silicon at 300 K the specific heat amounts to 1.6 MJ K⁻¹ m⁻³ (see also Chapter 6, Problem 6.6). So that C_th = 0.64 × 10⁻³ J K⁻¹

The temperature rises exponentially with time. However, since the switch-on time is much less than the thermal time constant, the temperature rise ΔT will increase almost proportionally to the time, according to the equation: ΔT(t) ≈ Pt/C_th. With t = 30 ms this yields ΔT = 47 × 10⁻³ K. During the measurement time the mean rise will amount to half of this value: ΔT ≈ 24 × 10⁻³ K.

(4) What would be the consequence of doubling the chip thickness for the temperature rise as calculated in part (3) of this problem?

When the chip thickness is doubled the thermal capacitance will also double. Therefore also the mean temperature rise will double. The thermal resistance will hardly be affected by changes in the chip thickness. Therefore, the temperature rise in stationary conditions, as calculated under part (1) of this problem, will hardly be affected.

(5) What is the mean temperature rise in the case of repetitive powering during 30 ms and intervals of 3 s?

The mean power dissipation amounts to Pt_m/(t_i + t_m) = 10⁻⁵ W. As a result of this mean power dissipation there will be a mean temperature rise ΔT_rep = P_mean/G_sg ≈ 0.009 K. This relatively small effect can be further reduced by enlarging the sensor area as suggested in answer (1).

Solution to Problem 7.2

Calculate the equivalent temperature errors for a 1 % change in I_s for the three sensors at 273 K.

For the transistor, from Equation (7.8) the well-known relation for the transconductance g_m is found:

This equation shows that a change in I_s of 1 % causes a change in V₀ (=V_BE) of approximately (kT/q) × 1 % = 0.24 mV. By using Equation (4.37) we can calculate the temperature dependence λ of V₀. Since at T = 0 K, V_BE0 = 1.27 V (mainly related to fundamental physical values), we find that λ = −2.27 mV K⁻¹. Therefore, the equivalent temperature error to be calculated is 0.24 mV/(2.27 mV K⁻¹) = 0.1 K.

For the thermistor we use Equation (7.7) to calculate that R⁻¹dR/dT = −1/(bT²) ≈ 6 % K⁻¹. Because V₀ is the linear product of the resistance and the current, a 1 % change in I_s is equivalent to a temperature error of 1 %/(6 % K⁻¹) = 0.17 K.

For the Pt resistor it can be found, using Equation (7.4), that R⁻¹dR/dT = R⁻¹R_pt(0){a − 2bt}. When T = 273 K and the values given in Section 7.3.1 are substituted in this equation we get a relative temperature sensitivity of 0.39 % K⁻¹. Consequently, a 1 % change in I_s is equivalent to 1 %/(0.39 % K⁻¹) = 2.6 K. This shows that the Pt resistor sensor is much more sensitive to change in the bias current than the transistor or the thermistor. Therefore, Pt resistors should always be used in configurations with (temperature-independent) reference resistors (see Chapter 10).

Solution to Problem 7.3

Calculate the minimum number N_min of periods of the sensor signal required to measure the temperature.

Since the sensor sensitivity is 0.5 % K⁻¹, the duty cycle varies from 0 to 1 for a temperature range of T_H − T_L = 200 K. For the minimum measurement time it holds that t_min = N_mint_p. When this equation is substituted in Equation (7.24) we get

Substitution of the given and calculated values yields N = 67 (t_m ≈ 20 ms).

Chapter 8

Solution to Problem 8.1

Find the effect of the capacitor C_gd on the current i₂.

Figure 8.8(b) shows an equivalent circuit model of the floating electrode structure.

(1) Capacitor C_g has no effect on the current i₂.

(2) The current i₂ is the sum of currents through capacitors C_o and C₂ and equals:

where s represents the Laplace operator.

The amplitude of the current i₂ is given by:

where f represents the frequency of the excitation signal V_m.

Calculate the values of current i₂ when the coupling capacitor has a value of C_gd = 1 pF and 100 pF

From Equation (16), it has been found that:

Solution to Problem 8.2

Find the minimum bandwidth of opamp.

As shown in Section 8.6.2, when the capacitance C_p2 and C_int are much larger than C_s, with a required accuracy of 10⁻⁵, the unity-gain bandwidth f_T of the opamp must satisfy the following condition:

With the given values of the components, it has been found that:

Solution to Problem 8.3

Please see the solution for the Problem 2.2 in Chapter 2.

Solution to Problem 8.4

Calculate the size of the voltage peaks at the output of the integrator.

During the charge phase (T₁), the capacitor C_s is charged to a value of V_exC_s and the capacitor C_off is charged to a value of V_comp,p–pC_off. At the moment t₁, the output of the integrator crosses the threshold level of the comparator. Then, the state of the comparator output is changed and the charge (V_exC_s + V_comp,p–pC_off) is transferred to the integrator capacitor C_int, via the switch S₃. This charge results in a voltage step at the output of the integrator, which equals:

During the discharge phase (T₂), only the capacitor C_off is charged to a value of V_comp,p–pC_off. At the moment t₂, the charge V_comp,p–pC_off is transferred to the integrator capacitor C_int. This charge results in a step at the output of the integrator:

Solution to Problem 8.5

(1) Calculate the effect of the shunting conductance G_s on the period T of the oscillator shown in Figure 8.16

The charge interval T₁ is not affected by the shunting conductance G_s because it is only determined by the charge V_comp,p–pC_off. The value of T₁ is given by Equation (8.10). Because of the shunting conductance G_s, during this phase, the capacitor C_s is charged to a value C_sV_ex/(1 + 2R_ONG_s). Therefore, the discharge period T₂ equals:

By summing the results from Equations (8.10) and (20), the period T of the oscillator output signal has been found to be:

(2) When V_comp,p–p = V_ex = 5 V, |I_ch| = 5μA, R_ON = 1 kΩ, G_s = 1 μS, and C_off = 1 pF and C_s = 2 pF, the relative error is:

Chapter 9

Solution to Problem 9.1: Hall device characteristics

(a) Hall coefficient

Equation (9.13): From well known characteristics of electrical properties for the silicon (e.g. http://www.ioffe.rssi.ru/SVA/NSM/Semicond/Si/electric.html#Hall), resistivity versus impurity concentration for Si at 300 K) the doping concentration corresponding to ρ = 1 Ω cm at 300 K is determined, to be N_D ≅ 4.5 × 10¹⁵ cm⁻³. At room temperature and such moderate doping level, all donors are ionized, and the density of quasi-free electrons corresponds to that of donors, that is n ≅ N_D. Thus

(b) Device resistance

(c) Current

(d) Hall voltage [1]

(e) Absolute sensitivity [2]

(f) Current-related sensitivity [3]

Solution to Problem 9.2: Noise of an integrated Hall device in silicon

The noise and its RMS value depend on the frequency range involved. Given the noise spectral density S_N(f), Equation (9.23), the RMS noise can be calculated as:

where f₁ and f₂ are the boundaries of the frequency range in which the noise is considered.

(a) Static mode

Two kinds of noise can be distinguished: thermal noise and flicker (1/f) noise with a corner frequency of 300 Hz. In the frequency bandwidth of 0.1 Hz to 100 Hz, 1/f noise dominates and thermal noise can be neglected. The noise spectral density can be described by a function

Thus

(b) Mode with implemented spinning current method

The noise spectral density is reduced to the thermal noise, i.e. a uniform distribution over the frequency, described by a constant

Thus

Then, the improvement factor of the spinning-current method on the micro-Hall device can be defined as

Chapter 10

Solution to Problem 10.1

(1) How large is the duty cycle of the output signal?

The current through R_CS amounts to (V_DD − V_DD/2)/R_CS = 0.2 μA. During the down-going slope of V_i, the current through R_CS is added to I_ref. Therefore, the current I_Ci through C_i amount to 1.2 μA. During the up-going slope of V_i, the current through R_CS is subtracted from the reverted I_ref. So that the magnitude of the current I_Ci through C_i amount to 0.8 μA. The ‘down’ time t_down and the ‘up’ time t_up are inversely proportional to these currents. Therefore, it holds that

(2) How large is the period time t_p of the output signal?

When R_CS → infinite, then according to Equation (10.1) t_down = t_up, so that for the period time t_p,infinite it holds that

where V_x = V_DD.

When R_CS = 10 MΩ, the charge and discharge currents amount to 1.2 μA and 0.8 μA, respectively (see the previous problem). Substitution of these current values in Equation (10.1) shows that

From Equations (24) and (25), it is found that the relative effect of R_CS corresponds to 4.3 %.

Solution to Problem 10.2

How large current i_Cs during the time interval t_i to t₂ ?

During the time interval t₁ to t₂, the output voltage is constant (V_i = V_ref). Because

it follows that i_Ci = 0 A. Therefore, during this time interval, it holds that i_CS = −I_ref.

Solution to Problem 10.3

(i) How large are the time intervals t_d,up and t_d,down?

For the up-going transient of the voltage V₂(t) it holds that

where τ = RC. For the moment t_d,up it holds that V₂(t)/V_DD = 0.25. Substitution of this value in Equation 27 yields t_d,up = 0.2878τ. In a similar way, it is found that t_d,down = 1.386τ.

(2) How large is the error ε_dc in the measured duty cycle?

For the measured duty cycle M_dc it holds that

where the last term in the right-hand side of Equation (28) represents the error in the duty cycle. On substitution of the calculated values for t_d,up and t_d,down and with τ = RC =1 μs, for the error ε_dc it is found that ε_dc = 0.0037 = 0.37 %.

Solution to Problem 10.4

(1) For the case that t_s = 200 ns, estimate the value of the measurement time t_mfor which quantization noise and white noise have equal standard deviations.

There is no correlation between quantization noise and white noise. Therefore for the total standard deviation σ_tot it holds that:

where σ_qn and σ_wn represent the standard deviations of the quantization noise and the white noise, respectively. To calculate the measurement time t_m at which σ_qn = σ_wn, we can rewrite Equation (10.7) as

where q = t_s/√6. White noise is inversely proportional to the square root of the measurement time, which can be explicitly be expressed as:

From Equations (30) and (31), we can find that σ_qn = σ_wn for a measurement time t_m,eq which equals

According to Equation (10.7), quantization noise decreases proportional with t_s. On the other hand, the value of t_s does not affect the magnitude of white noise. Therefore, the value of white noise can easily be found from the measurement results at the smallest value, being t_s = 14.2 ns. Considering these properties together with Equation (29), it can be concluded that for t_s = 14.2 ns and t_m = 14 ms (Figure 10.7) the effect of quantization noise is negligible. Therefore, for t_m = 14 ms we find that σ_wn = 0.58 × 10⁻⁴. Substitution of this value in Equation (29) shows that in the case of t_s = 200 ns (Figure 10.7(a)) it holds that σ_qn = 0.815 × 10⁻⁴. Substitution of these values in Equations (30) and (31) gives q = 1.14 × 10⁻⁶ s and r = 6.9 × 10⁻⁶ s^1/2. With these values and Equation (32) we find that t_m,eq = 27.6 ms.

(2) For the case that t_s = 1 ns, estimate the value of the measurement time t_mfor which quantization noise and white noise have equal standard deviations.

White noise is not affected by t_s, but quantization noise decreases proportionally with t_s. In the previous problem it has been found that for t_s = 200 ns, q = 1.14 × 10⁻⁶ s. At t_s = 14.2 ns, the q value q_fast is 14.2 ns/200 ns times smaller than that at 200 ns. From this it is found, that q_fast = 0.081 × 10⁻⁶ s. Substitution of this value and the r value in Equation (32) gives t_m,eq = 0.14 ms.

From these calculations, it can be concluded that sensor systems similar to that of Figures 10.7(c) and (d) cannot be improved by replacing for instance the asynchronous converter by a high resolution sigma–delta one. Instead of this, to improve the system performance, the white noise of the front-end circuitry has to be reduced.

Solution to Problem 10.5

(1) Calculate the relative error e_os caused by the offset voltage V_os.

The full-scale output voltage amounts to ±0.25 % of V_S,_DC, which corresponds to ±12.5 mV. The relative error caused by the offset voltage amounts to ±8 %.

(2) Calculate the relative error ε_sw caused by the switch resistances.

The equivalent resistance R_bridge between the terminals A and B, amounts to 1 kΩ. Because of the voltage drop across the switch resistances, the voltage V_AB across these terminals amounts to

The voltage drop over the switches causes a relative error, which equals the relative decrease of the voltage V_AB and amounts to about 17 %.

Solution to Problem 10.6

Calculate the relative error e_T caused by the interconnection of resistance-meter terminals.

By making the interconnection the sensor resistance is connected in series with wire resistance with a total equivalent series resistance of 1 Ω. The corresponding temperature error amounts to 2.5 K.

Chapter 11

(1) Taking into account that f_x <f_o, the measurement time must be calculated according to Equation (11.13). The answer is 20 ms.

(2) In the first case f_x > f₀, the measurement time must be calculated according the Equation (11.13), in the second case (f_x <f₀), according the Equation (11.14). The answers are 40ms and 13.3 ms, respectively.

(3) In order to be neglected, the UFDC's conversion error must be at least in two times less. So, a 0.001 % accuracy for the UFDC should be enough.

(4) The UFDC-1 can exchange accuracy for speed and vice versa. Hence, depending on the measuring conditions and algorithms in the DAQ system, the accuracy of the UFDC-1 can be decreased by up to 1 %. In this case, we will have the minimum possible measuring time. This is useful, for example, for some critical values in order to ensure action of the control system as soon as possible, for example in ABS, when a wheel is blocked. In the case of the maximum possible accuracy, the measuring time will be increased. For, example, such mode can be used in an ABS system at a nominal rotation speed in order to optimize engine performance.

Example: for frequency f_x = 25 kHz and reference frequency f₀ = 62.5kHz, measuring times at 1 % and 0.0035 % will be 1.64 ms and 457 ms, respectively.

References

1. http://www.melexis.com

2. Schott, Ch., Waser, J.-M. and Popovic, R.S. (2000). Single-chip 3-D silicon Hall sensor, Sensors and Actuators A: Physical, 82, 167–173.

3. Kejik, P., Schurig, E., Bergsma, F. and Popovic, R.S. (2005). First fully SMOS-integrated 3D Hall probe. In Proceedings of the 12th International Conference on Solid-State Sensors, Actuators and Microsystems, 5–9 June, Seoul, South Korea.