Chapter 2
Tests on the Mean
This chapter contains statistical tests on the mean of a normal population. Frequent questions are if the mean equals a specific value (mostly the null) or if two populations have the same mean or differ by a specific value. Depending on the sampling strategy and on knowledge of the data generation process, the assumptions of known or unknown variances must be distinguished. In most situations the variance is unknown–probably the reason why neither SAS nor R provides procedures to calculate tests for the case of known variances. However, rare situations exist where the variance of the underlying Gaussian distribution is known. We provide some code that demonstrates how these–so-called z-tests–can be calculated. If the variance has to be estimated from the sample, the test statistic distribution changes from standard normal to Student's t-distribution. Here the degrees of freedom vary depending on the specific test problem, for example, in the two population case on whether the variances are assumed to be equal or not. SAS by the procedure proc ttest and R by the function t.test provided convenient ways to calculate these tests. For k-sample tests (F-test) please refer to Chapter 17 which covers ANOVA tests.
2.1 One-sample tests
In this section we deal with the question, if the mean of a normal population differs from a predefined value. Whether the variance of the underlying Gaussian distribution is known or not determines the use of the z-test or the t-test.
2.1.1 z-test
| Description: |
Tests if a population mean 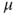 differs from a specific value differs from a specific value 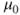 . . |
| Assumptions: |
- Data are measured on an interval or ratio scale.
- Data are randomly sampled from a Gaussian distribution.
- Standard deviation
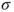 of the underlying Gaussian distribution is known. of the underlying Gaussian distribution is known.
|
| Hypotheses: |
(A)  vs vs 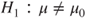 |
|
(B) 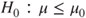 vs vs 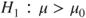 |
|
(C) 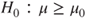 vs vs 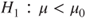 |
| Test statistic: |
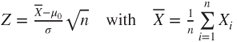 |
| Test decision: |
Reject  if for the observed value if for the observed value  of of  |
|
(A) 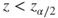 or or  |
|
(B) 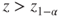 |
|
(C) 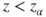 |
| p-value: |
(A)  |
|
(B) 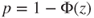 |
|
(C) 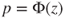 |
| Annotations: |
- The test statistic
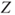 follows a standard normal distribution. follows a standard normal distribution.
 is the is the  -quantile of the standard normal distribution. -quantile of the standard normal distribution.- The assumption of an underlying Gaussian distribution can be relaxed if the sample size is large. Usually a sample size
 or or  is considered to be large enough. is considered to be large enough.
|
Example
To test the hypothesis that the mean systolic blood pressure in a certain population equals 140 mmHg. The standard deviation has a known value of 20 and a data set of 55 patients is available (dataset in
Table A.1).
SAS code
data blood_pressure;
set c.blood_pressure;
run;
* Calculate sample mean and total sample size;
proc means data=blood_pressure mean std;
var mmhg;
output out=ztest01 mean=meanvalue n=n_total;
run;
* Calculate test-statistic and p-values;
data ztest02;
set ztest01;
format p_value_A p_value_B p_value_C pvalue.;
mu0=140; * Set mean value under the null hypothesis;
sigma=20; * Set known sigma;
z=sqrt(n_total)*(meanvalue-mu0)/sigma;
p_value_A=2*probnorm(-abs(z));
p_value_B=1-probnorm(z);
p_value_C=probnorm(z);
run;
* Output results;
proc print;
var z p_value_A p_value_B p_value_C ;
run;
SAS output
z p_value_A p_value_B p_value_C
-3.70810 0.0002 0.9999 0.0001
Remarks:
- There is no SAS procedure to calculate the one-sample z-test directly.
- The above code also shows how to calculate the p-values for the one-sided tests (B) and (C).
R code
# Calculate sample mean and total sample size
xbar<-mean(blood_pressure$mmhg)
n<-length(blood_pressure$mmhg)
# Set mean value under the null hypothesis
mu0<-140
# Set known sigma
sigma<-20
# Calculate test statistic and p-values
z<-sqrt(n)*(xbar-mu0)/sigma
p_value_A=2*pnorm(-abs(z))
p_value_B=1-pnorm(z)
p_value_C=pnorm(z)
# Output results
z
p_value_A
p_value_B
p_value_C
R output
> z
[1] -3.708099
> p_value_A
[1] 0.0002088208
> p_value_B
[1] 0.9998956
> p_value_C
[1] 0.0001044104
Remarks:
- There is no basic R function to calculate the one-sample z-test directly.
- The above code also shows how to calculate the p-values for the one-sided tests (B) and (C).
2.1.2 t-test
| Description: |
Tests if a population mean  differs from a specific value differs from a specific value 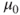 . . |
| Assumptions: |
- Data are measured on an interval or ratio scale.
- Data are randomly sampled from a Gaussian distribution.
- Standard deviation
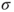 of the underlying Gaussian distribution is unknown and estimated by the population standard deviation of the underlying Gaussian distribution is unknown and estimated by the population standard deviation 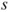 . .
|
| Hypotheses: |
(A) 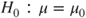 vs vs  |
|
(B) 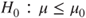 vs vs 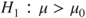 |
|
(C) 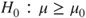 vs vs  |
| Test statistic: |
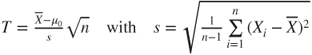 |
| Test decision: |
Reject 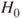 if for the observed value if for the observed value  of of 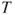 |
|
(A) 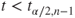 or or 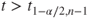 |
|
(B) 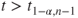 |
|
(C)  |
| p-value: |
(A)  |
|
(B) 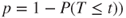 |
|
(C) 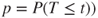 |
| Annotations: |
- The test statistic
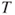 is t-distributed with is t-distributed with  degrees of freedom. degrees of freedom.
 is the is the 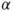 -quantile of the t-distribution with -quantile of the t-distribution with 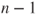 degrees of freedom. degrees of freedom.- The assumption of an underlying Gaussian distribution can be relaxed if the sample size is large. Usually a sample size
 is considered to be large enough. is considered to be large enough.
|
Example
To test the hypothesis that the mean systolic blood pressure in a certain population equals 140 mmHg. The dataset at hand has measurements on 55 patients (dataset in
Table A.1).
SAS code
proc ttest data=blood_pressure ho=140 sides=2;
var mmhg;
run;
SAS output
DF t Value Pr < t
54 -3.87 0.0003
Remarks:
- ho=value is optional and defines the value
 to test against. Default is 0.
to test against. Default is 0.
- sides=value is optional and defines the type of alternative hypothesis: 2=two sided (A); U=true mean is greater (B); L=true mean is lower (C). Default is 2.
R code
t.test(blood_pressure$mmhg,mu=140,alternative="two.sided")
R output
t = -3.8693, df = 54, p-value = 0.0002961
Remarks:
- mu=value is optional and defines the value
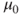 to test against. Default is 0.
to test against. Default is 0.
- alternative=“value” is optional and defines the type of alternative hypothesis: “two.sided”= two sided (A); “greater”=true mean is greater (B); “less”=true mean is lower (C). Default is “two.sided”.
2.2 Two-sample tests
This section covers two-sample tests, to test if either the means of two populations differ from each other or if the mean difference of paired populations differ from a specific value.
2.2.1 Two-sample z-test
| Description: |
Tests if two population means 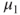 and and  differ less than, more than or by a value differ less than, more than or by a value 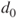 . . |
| Assumptions: |
- Data are measured on an interval or ratio scale.
- Data are randomly sampled from two independent Gaussian distributions.
- The standard deviations
 and and 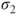 of the underlying Gaussian distributions are known. of the underlying Gaussian distributions are known.
|
| Hypotheses: |
(A)  vs vs 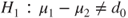 |
|
(B)  vs vs 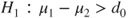 |
|
(C) 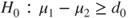 vs vs 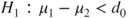 |
| Test statistic: |
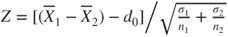 |
| Test decision: |
Reject 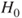 if for the observed value if for the observed value 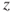 of of 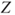 |
|
(A)  or or 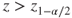 |
|
(B)  |
|
(C)  |
| p-value: |
(A) 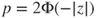 |
|
(B)  |
|
(C)  |
| Annotations: |
- The test statistic
 is a standard normal distribution. is a standard normal distribution.
 is the is the 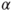 -quantile of the standard normal distribution. -quantile of the standard normal distribution.- The assumption of an underlying Gaussian distribution can be relaxed if the sample size is large. Usually sample sizes
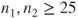 or or 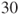 for both distributions are considered to be large enough. for both distributions are considered to be large enough.
|
Example
To test the hypothesis that the mean systolic blood pressures of healthy subjects (status=0) and subjects with hypertension (status=1) are equal (

) with known standard deviations of

and
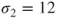
. The dataset contains
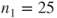
subjects with status 0 and
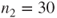
with status 1 (dataset in
Table A.1).
SAS code
* Calculate the two means and sample sizes
proc means data=blood_pressure mean;
var mmhg;
by status;
output out=ztest01 mean=meanvalue n=n_total;
run;
* Output of the means in two different datasets;
data ztest02 ztest03;
set ztest01;
if status=0 then output ztest02;
if status=1 then output ztest03;
run;
* Rename mean and sample size of subjects
with status=0;
data ztest02;
set ztest02;
rename meanvalue=mean_status0
n_total=n_status0;
run;
* Rename mean and sample size of subjects
with status=1;
data ztest03;
set ztest03;
rename meanvalue=mean_status1
n_total=n_status1;
run;
* Calculate test statistic and two-sided p-value;
data ztest04;
merge ztest02 ztest03;
* Set difference to be tested;
d0=0;
* Set standard deviation of sample with status 0;
sigma0=10;
* Set standard deviation of sample with status 1;
sigma1=12;
format p_value pvalue.;
z= ((mean_status0-mean_status1)-d0)
/ sqrt(sigma0**2/n_status0+sigma1**2/n_status1);
p_value=2*probnorm(-abs(z));
run;
* Output results;
proc print;
var z p_value;
run;
SAS output
z p_value
-10.5557 <.0001
Remarks:
- There is no SAS procedure to calculate the two-sample z-test directly.
- The one-sided p-value for hypothesis (B) can be calculated with p_value_B=1-probnorm(z) and the p-value for hypothesis (C) with p_value_C=probnorm(z).
R code
# Set difference to be tested;
d0<-0
# Set standard deviation of sample with status 0
sigma0<-10
# Set standard deviation of sample with status 1
sigma1<-12
# Calculate the two means
mean_status0<-
mean(blood_pressure$mmhg[blood_pressure$status==0])
mean_status1<-
mean(blood_pressure$mmhg[blood_pressure$status==1])
# Calculate both sample sizes
n_status0<-
length(blood_pressure$mmhg[blood_pressure$status==0])
n_status1<-
length(blood_pressure$mmhg[blood_pressure$status==1])
# Calculate test statistic and two-sided p-value
z<-((mean_status0-mean_status1)-d0)/
sqrt(sigma0∧2/n_status0+sigma1∧2/n_status1)
p_value=2*pnorm(-abs(z))
# Output results
z
p_value
R output
> z
[1] -10.55572
> p_value
[1] 4.779482e-26
Remarks:
- There is no basic R function to calculate the two-sample z-test directly.
- The one-sided p-value for hypothesis (B) can be calculated with p_value_B=1-pnorm(z) and the p-value for hypothesis (C) with p_value_C=pnorm(z).
2.2.2 Two-sample pooled t-test
| Description: |
Tests if two population means  and and  differ less than, more than or by a value differ less than, more than or by a value 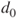 . . |
| Assumptions: |
- Data are measured on an interval or ratio scale.
- Data are randomly sampled from two independent Gaussian distributions.
- Standard deviations
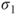 and and 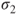 of the underlying Gaussian distributions are unknown but equal and estimated through the pooled population standard deviation of the underlying Gaussian distributions are unknown but equal and estimated through the pooled population standard deviation  . .
|
| Hypotheses: |
(A) 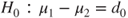 vs vs 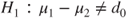 |
|
(B)  vs vs 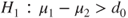 |
|
(C)  vs vs  |
| Test statistic: |
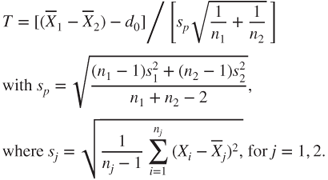 |
| Test decision: |
Reject 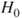 if for the observed value if for the observed value 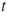 of of 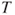 |
|
(A) 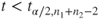 or or  |
|
(B) 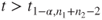 |
|
(C)  |
| p-value: |
(A)  |
|
(B)  |
|
(C)  |
| Annotations: |
- The test statistic
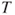 is t-distributed with is t-distributed with 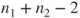 degrees of freedom. degrees of freedom.
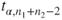 is the is the  -quantile of the t-distribution with -quantile of the t-distribution with  degrees of freedom. degrees of freedom.- The assumption of two underlying Gaussian distributions can be relaxed if the sample sizes of both samples are large. Usually sample sizes
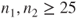 or or  for both distributions are considered to be large enough. for both distributions are considered to be large enough.
|
Example
To test the hypothesis that the mean systolic blood pressures of healthy subjects (status=0) and subjects with hypertension (status=1) are equal, hence

. The dataset contains
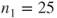
subjects with status 0 and

with status 1 (dataset in
Table A.1).
SAS code
proc ttest data=blood_pressure h0=0 sides=2;
class status;
var mmhg;
run;
SAS output
Method Variances DF t Value Pr> |t|
Pooled Equal 53 -10.47 <.0001
Remarks:
- h0=value is optional and defines the value
 to test against. Default is 0.
to test against. Default is 0.
- sides=value is optional and defines the type of alternative hypothesis: 2= two sided (A); U=true mean difference is greater (B); L=true mean difference is lower (C). Default is 2.
R code
status0<-blood_pressure$mmhg[blood_pressure$status==0]
status1<-blood_pressure$mmhg[blood_pressure$status==1]
t.test(status0,status1,mu=0,alternative="two.sided",
var.equal=TRUE)
R output
t = -10.4679, df = 53, p-value = 1.660e-14
Remarks:
- mu=value is optional and defines the value
 to test against. Default is 0.
to test against. Default is 0.
- alternative=“value” is optional and defines the type of alternative hypothesis: “two.sided”= two sided (A); “greater”=true mean difference is greater (B); “less”=true mean difference is lower (C). Default is “two.sided”.
2.2.3 Welch test
| Description: |
Tests if two population means  and and  differ less than, more than or by a value differ less than, more than or by a value  . . |
| Assumptions: |
- Data are measured on an interval or ratio scale.
- Data are randomly sampled from two independent Gaussian distributions.
- Standard deviations
 and and 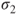 of the underlying Gaussian distributions are unknown and not necessarily equal; estimated through the population standard deviation of each sample. of the underlying Gaussian distributions are unknown and not necessarily equal; estimated through the population standard deviation of each sample.
|
| Hypotheses: |
(A) 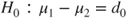 vs vs  |
|
(B)  vs vs  |
|
(C)  vs vs 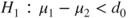 |
| Test statistic: |
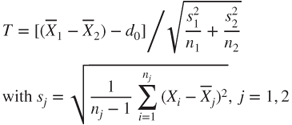 |
| Test decision: |
Reject  if for the observed value if for the observed value 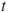 of of  |
|
(A)  or or  |
|
(B)  |
|
(C)  |
| p-value: |
(A)  |
|
(B) 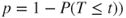 |
|
(C)  |
| Annotations: |
- This test is also known as a two-sample t-test or Welch–Satterthwaite test
- The test statistic
 approximately follows a t-distribution with approximately follows a t-distribution with  degrees of freedom [Bernard Welch (1947) and Franklin Satterthwaite (1946) approximation]. degrees of freedom [Bernard Welch (1947) and Franklin Satterthwaite (1946) approximation].
 is the is the  -quantile of the t-distribution with -quantile of the t-distribution with  degrees of freedom. degrees of freedom.- William Cochran and Gertrude Cox (1950) proposed an alternative way to calculate critical values for the test statistic.
- The assumption of two underlying Gaussian distributions can be relaxed if the sample sizes of both samples are large. Usually sample sizes
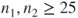 or or 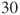 for both distributions are considered to be large enough. for both distributions are considered to be large enough.
|
Example
To test the hypothesis that the mean systolic blood pressures of healthy subjects (status=0) and subjects with hypertension (status=1) are equal, hence

. The dataset contains

subjects with status 0 and
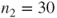
with status 1 (dataset in
Table A.1).
SAS code
proc ttest data=blood_pressure h0=0 sides=2 cochran;
class status;
var mmhg;
run;
SAS output
Method Variances DF t Value Pr> |t|
Satterthwaite Unequal 50.886 -10.45 <.0001
Cochran Unequal . -10.45 0.0001
Remarks:
- The optional command cochran forces SAS to calculate the p-value according to the Cochran and Cox approximation.
- h0=value is optional and defines the value
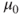 to test against. Default is 0.
to test against. Default is 0.
- sides=value is optional and defines the type of alternative hypothesis: 2=two sided (A); U=true mean difference is greater (B); L=true mean difference is lower (C). Default is 2.
R code
status0<-blood_pressure$mmhg[blood_pressure$status==0]
status1<-blood_pressure$mmhg[blood_pressure$status==1]
t.test(status0,status1,mu=0,alternative="two.sided",
var.equal=FALSE)
R output
t = -10.4506, df = 50.886, p-value = 2.887e-14
Remarks:
- mu=value is optional and defines the value
 to test against. Default is 0.
to test against. Default is 0.
- The option var.equal=FALSE enables the Welch test.
- alternative=“value” is optional and indicates the type of alternative hypothesis: “two.sided”=two sided (A); “greater”=true mean difference is greater (B); “less”=true mean difference is lower (C). Default is “two.sided”.
- By default R has no option to calculate the Cochran and Cox approximation.
2.2.4 Paired z-test
| Description: |
Tests if the difference of two population means  differs from a value differs from a value  in the case that observations are collected in pairs. in the case that observations are collected in pairs. |
| Assumptions: |
- Data are measured on an interval or ratio scale and randomly sampled in pairs
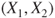 . .
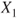 follows a Gaussian distribution with mean follows a Gaussian distribution with mean  and variance and variance  . . 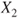 follows a Gaussian distribution with mean follows a Gaussian distribution with mean  and variance and variance  . The covariance of . The covariance of  and and  is is  . .- The standard deviation
 of the differences of the differences 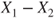 is known. is known.
|
| Hypotheses: |
(A)  vs vs  |
|
(B) 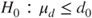 vs vs 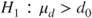 |
|
(C) 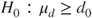 vs vs 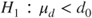 |
| Test statistic: |
 |
| Test decision: |
Reject  if for the observed value if for the observed value  of of  |
|
(A)  or or  |
|
(B) 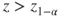 |
|
(C) 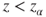 |
| p-value: |
(A)  |
|
(B)  |
|
(C)  |
| Annotations: |
- The test statistic
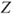 follows a standard normal distribution. follows a standard normal distribution.
 is the is the 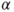 -quantile of the standard normal distribution. -quantile of the standard normal distribution.- The assumption of a Gaussian distribution can be relaxed if the distribution of the differences is symmetric.
|
Example
To test if the mean intelligence quotient increases by 10 comparing before training (IQ1) and after training (IQ2) (dataset in
Table A.2). It is known that the standard deviation of the difference is 1.40. Note: Because we are interested in a negative difference of means of
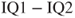
, we must test against
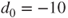
.
SAS code
* Calculate the difference of each observation;
data iq_diff;
set iq;
diff=iq1-iq2;
run;
* Calculate the mean and sample size;
proc means data=iq_diff mean;
var diff;
output out=ztest mean=mean_diff n=n_total;
run;
* Calculate test statistic and two-sided p-value;
data ztest;
set ztest;
d0=-10; * Set difference to test;
sigma_diff= 1.40; * Set standard deviation;
format p_value pvalue.;
z= sqrt(n_total)*((mean_diff-d0)/sigma_diff);
p_value=2*probnorm(-abs(z));
run;
* Output results;
proc print;
var z p_value;
run;
SAS output
z p_value
-1.27775 0.2013
Remarks:
- There is no SAS procedure to calculate this test directly.
- The one-sided p-value for hypothesis (B) can be calculated with p_value_B=1-probnorm(z) and the p-value for hypothesis (C) with p_value_C=probnorm(z).
R code
# Set difference to test;
d0<--10
# Set standard deviation of the difference
sigma_diff<-1.40
# Calculate the mean of the difference
mean_diff<-mean(iq$IQ1-iq$IQ2)
# Calculate the sample size
n_total<-length(iq$IQ1)
# Calculate test statistic and two-sided p-value
z<-sqrt(n_total)*((mean_diff-d0)/sigma_diff)
p_value=2*pnorm(-abs(z))
# Output results
z
p_value
R output
> z
[1] -1.277753
> p_value
[1] 0.2013365
Remarks:
- There is no basic R function to calculate the two-sample z-test directly.
- The one-sided p-value for hypothesis (B) can be calculated with p_value_B=1-pnorm(z) and the p-value for hypothesis (C) with p_value_C=pnorm(z).
2.2.5 Paired t-test
| Description: |
Tests if the difference of two population means  differs from a value differs from a value 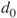 in the case that observations are collected in pairs. in the case that observations are collected in pairs. |
| Assumptions: |
- Data are measured on an interval or ratio scale and randomly sampled in pairs
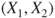 . .
 follows a Gaussian distribution with mean follows a Gaussian distribution with mean  and variance and variance 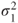 . .  follows a Gaussian distribution with mean follows a Gaussian distribution with mean  and variance and variance  . The covariance of . The covariance of  and and 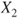 is is  . . |
|
- The standard deviations are unknown. The standard deviation
 of the differences is estimated through the population standard deviation of the differences is estimated through the population standard deviation 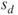 of the differences. of the differences.
|
| Hypotheses: |
(A) 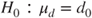 vs vs  |
|
(B) 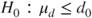 vs vs  |
|
(C)  vs vs 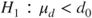 |
| Test statistic: |
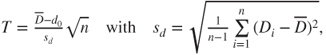 |
|
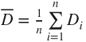 and and  |
| Test decision: |
Reject  if for the observed value if for the observed value  of of  |
|
(A)  or or 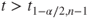 |
|
(B)  |
|
(C)  |
| p-value: |
(A) 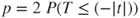 |
|
(B)  |
|
(C) 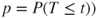 |
| Annotations: |
- The test statistic
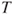 is t-distributed with is t-distributed with 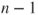 degrees of freedom. degrees of freedom.
 is the is the 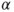 -quantile of the t-distribution with -quantile of the t-distribution with  degrees of freedom. degrees of freedom.- The assumption of a Gaussian distribution can be relaxed if the distribution of the differences is symmetric.
|
Example
To test if the mean intelligence quotient increases by 10 comparing before training (IQ1) and after training (IQ2) (dataset in
Table A.2). Note: Because we are interested in a negative difference of means of

, we must test against

.
SAS code
proc ttest data=iq h0=-10 sides=2;
paired iq1*iq2;
run;
SAS output
DF t Value Pr> |t|
19 -1.29 0.2141
Remarks:
- The command paired forces SAS to calculate the paired t-test. Do not forget the asterisk between the variable names.
- h0=value is optional and indicates the value
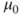 to test against. Default is 0.
to test against. Default is 0.
- sides=value is optional and indicates the type of alternative hypothesis: 2=two sided (A); U=true mean is greater (B); L=true mean is lower (C). Default is 2.
R code
t.test(iq$IQ1,iq$IQ2,mu=-10,alternative="two.sided",
paired=TRUE)
R output
t = -1.2854, df = 19, p-value = 0.2141
Remarks:
- The command paired=TRUE forces R to calculate the paired t-test.
- mu=value is optional and indicates the value
 to test against. Default is 0.
to test against. Default is 0.
- alternative=“value” is optional and indicates the type of alternative hypothesis: “two.sides”=two sided (A); “greater”=true mean is greater (B); “less”=true mean is lower (C). Default is “two.sided”.
References
Cochran W.G. and Cox G.M. 1950 Experimental Designs. John Wiley & Sons, Ltd.
Satterthwaite F.E. 1946 An approximate distribution of estimates of variance components. Biometrics Bulletin 2, 110–114.
Welch B.L. 1947 The generalization of Student's problem when several different population variances are involved. Biometrika 34, 28–35.
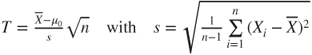
 to test against. Default is 0.
to test against. Default is 0.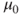 to test against. Default is 0.
to test against. Default is 0.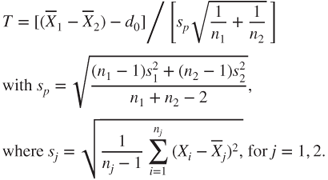
 to test against. Default is 0.
to test against. Default is 0.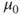 to test against. Default is 0.
to test against. Default is 0.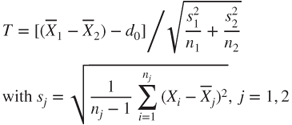
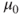 to test against. Default is 0.
to test against. Default is 0. to test against. Default is 0.
to test against. Default is 0.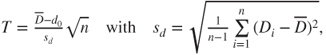
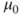 to test against. Default is 0.
to test against. Default is 0. to test against. Default is 0.
to test against. Default is 0.