Chapter 4
Tests on proportions
In this chapter we present tests for the parameter of a binomial distribution. We first treat a test on the population proportion in the one-sample case. We further cover tests for the difference of two proportions using the pooled as well as the unpooled variances. The last test in this chapter deals with the equality of proportions for the multi-sample case. Not all tests are covered by a SAS procedure or R function. We give the appropriate sample code to perform all discussed tests.
4.1 One-sample tests
In this section we deal with the question, if a population proportion differs from a predefined value between 0 and 1.
4.1.1 Binomial test
| Description: |
Tests if a population proportion  differs from a value differs from a value  . . |
| Assumptions: |
- Data are randomly sampled from a large population with two possible outcomes.
- Let
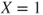 be denoted as “success” and be denoted as “success” and  as “failure”. as “failure”.
- The parameter
 of interest is given by the proportion of successes in the population. of interest is given by the proportion of successes in the population.
- The number of successes
 in a random sample of size in a random sample of size  follows a binomial distribution follows a binomial distribution  . .
|
| Hypothesis: |
(A) 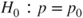 vs vs 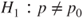 |
|
(B) 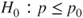 vs vs  |
|
(C)  vs vs 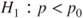 |
| Test statistic: |
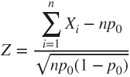 |
| Test decision: |
Reject 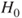 if for the observed value if for the observed value  of of  |
|
(A)  or or  |
|
(B)  |
|
(C)  |
| p-value: |
(A) 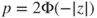 |
|
(B)  |
|
(C)  |
| Annotation: |
- This is the large sample test. If the sample size is large [rule of thumb:
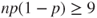 ] the test statistic ] the test statistic 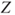 is approximately a standard normal distribution. is approximately a standard normal distribution.
- For small samples an exact test with
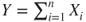 as test statistic and critical regions based on the binomial distribution are used. as test statistic and critical regions based on the binomial distribution are used.
|
|
Example
To test the hypothesis that the proportion of defective workpieces of a machine equals 50%. The available dataset contains

observations (dataset in
Table A.4).
SAS code
*** Version 1 ***;
* Only for hypothesis (A) and (C);
proc freq data=malfunction;
tables malfunction / binomial(level='1' p=.5 correct);
exact binomial;
run;
*** Version 2 ***;
* For hypothesis (A), (B), and (C);
* Calculate the numbers of successes and failures;
proc sort data=malfunction;
by malfunction;
run;
proc summary data=malfunction n;
var malfunction;
by malfunction;
output out=ptest01 n=n;
run;
* Retrieve the number of successe and failures;
data ptest02 ptest03;;
set ptest01;
if malfunction=0 then output ptest02;
if malfunction=1 then output ptest03;
run;
* Rename number of failures;
data ptest02;
set ptest02;
rename n=failures;
drop malfunction _TYPE_ _FREQ_;
run;
* Rename number of successes;
data ptest03;
set ptest03;
rename n=successes;
drop malfunction _TYPE_ _FREQ_;
run;
* Calculate test statistic and p-values;
data ptest04;
merge ptest02 ptest03;
format test $20.;
n=successes+failures;
* Estimated Proportion;
p_estimate=successes/n;
* Proportion to test;
p0=0.5;
* Perform exact test;
test="Exact";
p_value_B=probbnml(p0,n,failures);
p_value_C=probbnml(p0,n,successes);
p_value_A=2*min(p_value_B,p_value_c);
output;
* Perform asymptotic test;
test="Asymptotic";
Z=(successes-n*p0)/sqrt((n*p0*(1-p0)));
p_value_A=2*probnorm(-abs(Z));
p_value_B=1-probnorm(-abs(Z));
p_value_C=probnorm(-abs(Z));
output;
* Perform asymptotic test with continuity correction;
test=“Asymptotic with correction”;
Z=(abs(successes-n*p0)-0.5)/sqrt((n*p0*(1-p0)));
p_value_A=2*probnorm(-abs(Z));
p_value_B=1-probnorm(-abs(Z));
p_value_C=probnorm(-abs(Z));
output;
run;
* Output results;
proc print;
var test Z p_estimate p0 p_value_A p_value_B p_value_C;
run;
SAS output
Version 1
Test of H0: Proportion = 0.5
ASE under H0 0.0791
Z -1.4230
One-sided Pr < Z 0.0774
Two-sided Pr > |Z| 0.1547
Exact Test
One-sided Pr <= P 0.0769
Two-sided = 2 * One-sided 0.1539
The asymptotic confidence limits and test
include a continuity correction.
Version 2
test p_value_A p_value_B p_value_C
Exact 0.15386 0.95965 0.076930
Asymptotic 0.11385 0.94308 0.056923
Asymptotic with corr 0.15473 0.92264 0.077364
Remarks:
- PROC FREQ is the easiest way to perform the binomial test, but the procedure calculates p-values only for hypotheses (A) and (C).
- level= indicates the variable level for successes.
- p= specifies p0. The default is 0.5.
- correct requests the asymptotic test with continuity correction. This yields a better approximation in some cases by subtracting 0.5 in the numerator if
 and adding 0.5 otherwise. Omitting this option will result in a test without continuity correction.
and adding 0.5 otherwise. Omitting this option will result in a test without continuity correction.
- exact binomial forces SAS to perform the exact test as well.
R code
# Number of observations
n<-length(malfunction$malfunction)
# Number of successes
d<-length(malfunction$malfunction
[malfunction$malfunction==1])
# Proportion to test
p0<-0.5
# Exact test
binom.test(d,n,p0,alternative="two.sided")
# Asymptotic test
prop.test(d,n,p0,alternative="two.sided",correct=TRUE)
R output
Exact binomial test
number of successes = 15, number of trials = 40,
p-value = 0.1539
1-sample proportions test with continuity correction
X-squared = 2.025, df = 1, p-value = 0.1547
Remarks:
- The function binom.test calculates the exact test and the function prop.test the asymptotic test.
- The first parameter of both functions is for the number of successes, the second parameter for the number of trials and the third parameter for the proportion to test for.
- alternative=“value” is optional and indicates the type of alternative hypothesis: “two.sided”= two sided (A); “greater”=true proportion is greater (B); “less”=true proportion is lower (C). Default is “two.sided”.
- The asymptotic test provides an additional parameter. With “corrected=TRUE” the test with continuity correction is applied. This yields a better approximation in some cases. A Yates' continuity correction is applied, but only if
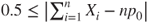 . The default value is “correct=FALSE”.
. The default value is “correct=FALSE”.
- Because the test statistics of the one-sample proportion test and the
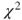 -test for one-way tables are equivalent, R uses the latter test.
-test for one-way tables are equivalent, R uses the latter test.
4.2 Two-sample tests
In this section we deal with the question, if proportions of two independent populations differ from each other. We present two tests for this problem (Keller and Warrack 1997). In the first case the standard deviations of both distributions may differ from each other. In the second case equal but unknown standard deviations are assumed such that both samples can be pooled to obtain a better estimate of the standard deviation. Both presented tests are based on an asymptotic standard normal distribution.
4.2.1 z-test for the difference of two proportions (unpooled variances)
| Description: |
Tests if two population proportions 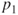 and and  differ by a specific value differ by a specific value  . . |
| Assumptions: |
- Data are randomly sampled with two possible outcomes.
- Let
 be denoted as “success” and be denoted as “success” and 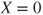 as “failure”. as “failure”.
- The parameters
 and and  are the proportions of success in the two populations. are the proportions of success in the two populations.
- Data are randomly sampled from two populations with sample sizes
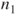 and and 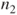 . .
- The number of successes
 in the in the  sample follows a binomial distribution sample follows a binomial distribution  , , 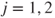 . .
|
| Hypothesis: |
(A)  vs vs 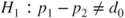 |
|
(B)  vs vs 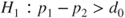 |
|
(C)  vs vs  |
| Test statistic: |
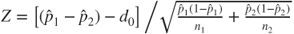 |
|
where  and and  |
| Test decision: |
Reject  if for the observed value if for the observed value 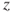 of of 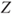 |
|
(A)  or or 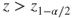 |
|
(B) 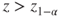 |
|
(C)  |
| p-value: |
(A)  |
|
(B) 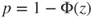 |
|
(C)  |
| Annotation: |
- This is a large sample test. If the sample size is large enough the test statistic
 is a standard normal distribution. As a rule of thumb is a standard normal distribution. As a rule of thumb  , , 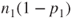 , , 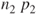 and and 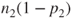 should all be should all be 
|
Example
To test the hypothesis that the proportion of defective workpieces of company A and company B differ by 10%. The dataset contains
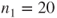
observations from company A and

observations from company B (dataset in
Table A.4).
SAS code
* Determining sample sizes and number of successes;
proc means data=malfunction n sum;
var malfunction;
by company;
output out=prop1 n=n sum=success;
run;
* Retrieve these results as two separate datasets;
data propA propB;
set prop1;
if company="A" then output propA;
if company="B" then output propB;
run;
* Relative frequencies of successes for company A;
data propA;
set propA;
keep n success p1;
rename n=n1
success=success1;
p1=success/n;
run;
* Relative frequencies of successes for company B;
data propB;
set propB;
keep n success p2;
rename n=n2
success=success2;
p2=success/n;
run;
* Merge datasets of company A and B;
data prop2;
merge propA propB;
run;
* Calculate test statistic and p-value;
data prop3;
set prop2;
format p_value pvalue.;
p_diff=p1-p2; *Difference of proportions;
d0=0.10; *Difference to be tested;
* Test statistic and p-values;
z=(p_diff-d0)/sqrt((p1*(1-p1))/n1 + (p2*(1-p2))/n2);
p_value=2*probnorm(-abs(z));
run;
proc print;
var z p_value;
run;
SAS output
z p_value
1.75142 0.0799
Remarks:
- There is no SAS procedure to calculate this test directly.
- The data do not fulfill the criteria to ensure that the test statistic
 is a Gaussian distribution, because
is a Gaussian distribution, because  , therefore the p-value is questionable.
, therefore the p-value is questionable.
R code
# Number of observations for company A
n1<-length(malfunction$malfunction
[malfunction$company=='A'])
# Number of successes for company A
s1<-length(malfunction$malfunction[malfunction$company=='A'
& malfunction$malfunction==1])
# Number of observations for company B
n2<-length(malfunction$malfunction
[malfunction$company=='B'])
# Number of successes for company B
s2<-length(malfunction$malfunction[malfunction$company=='B'
& malfunction$malfunction==1])
# Proportions
p1=s1/n1
p2=s2/n2
# Difference of proportions
p_diff=p1-p2
# Difference to test
d0=0.10
# Test statistic and p-values
z=(p_diff-d0)/sqrt((p1*(1-p1))/n1 + (p2*(1-p2))/n2)
p_value=2*pnorm(-abs(z))
# Output results
z
p_value
R output
> z
[1] 1.751424
> p_value
[1] 0.07987297
Remarks:
- There is no R function to calculate this test directly.
- The data do not fulfill the criteria to ensure that the test statistic
 is a Gaussian distribution, because
is a Gaussian distribution, because  , therefore the p-value is questionable.
, therefore the p-value is questionable.
4.2.2 z-test for the equality between two proportions (pooled variances)
| Description: |
Tests if two population proportions  and and 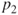 differ from each other. differ from each other. |
| Assumptions: |
- Data are randomly sampled with two possible outcomes.
- Let
 be denoted as “success” and be denoted as “success” and  as “failure”. as “failure”.
- The parameters
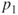 and and  are the proportions of success in the two populations. are the proportions of success in the two populations.
- Data are randomly sampled from two populations with sample sizes
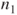 and and 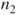 . .
- The number of successes
 in the in the  sample follow a binomial distribution sample follow a binomial distribution 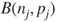 , , 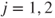 . .
|
| Hypothesis: |
(A) 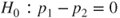 vs vs 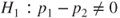 |
|
(B)  vs vs  |
|
(C)  vs vs 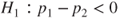 |
| Test statistic: |
 |
|
where  and and  |
| Test decision: |
Reject  if for the observed value if for the observed value  of of 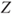 |
|
(A) 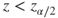 or or 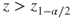 |
|
(B)  |
|
(C)  |
| p-value: |
(A) 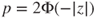 |
|
(B) 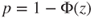 |
|
(C) 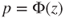 |
| Annotation: |
- This is a large sample test. If the sample size is large enough the test statistic
 is a standard normal distribution. As a rule of thumb following is a standard normal distribution. As a rule of thumb following 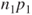 , , 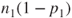 , ,  and and  should all be should all be 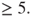
- This test is equivalent to the
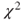 -test of a -test of a 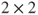 table, that is, table, that is,  . The advantage of the . The advantage of the 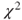 -test is that there exists an exact test for small samples, which calculates the p-values from the exact distribution. This test is the famous Fisher's exact test. More information is given in Chapter 14. -test is that there exists an exact test for small samples, which calculates the p-values from the exact distribution. This test is the famous Fisher's exact test. More information is given in Chapter 14.
|
Example
To test the hypothesis that the proportion of defective workpieces of company A and company B are equal. The dataset contains

observations from company A and
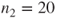
observations from company B (dataset in
Table A.4).
SAS code
* Determining sample sizes and number of successes;
proc means data=malfunction n sum;
var malfunction;
by company;
output out=prop1 n=n sum=success;
run;
* Retrieve these results in two separate datasets;
data propA propB;
set prop1;
if company="A" then output propA;
if company="B" then output propB;
run;
* Relative frequencies of successes for company A;
data propA;
set propA;
keep n success p1;
rename n=n1
success=success1;
p1=success/n;
run;
* Relative frequencies of successes for company B;
data propB;
set propB;
keep n success p2;
rename n=n2
success=success2;
p2=success/n;
run;
* Merge datasets of company A and B;
data prop2;
merge propA propB;
run;
* Calculate test statistic and p-value;
data prop3;
set prop2;
format p_value pvalue.;
* Test statistic and p-values;
p=(p1*n1+p2*n2)/(n1+n2);
z=(p1-p2)/sqrt((p*(1-p))*(1/n1+1/n2));
p_value=2*probnorm(-abs(z));
run;
proc print;
var z p_value;
run;
SAS output
z p_value
2.28619 0.0222
Remarks:
- There is no SAS procedure to calculate this test directly.
- The data do not fulfill the criteria to ensure that the test statistic
 is a Gaussian distribution, because
is a Gaussian distribution, because  . In this case it is better to use Fisher's exact test, see Chapter 14.
. In this case it is better to use Fisher's exact test, see Chapter 14.
R code
# Number of observations for company A
n1<-length(malfunction$malfunction
[malfunction$company=='A'])
# Number of successes for company A
s1<-length(malfunction$malfunction[malfunction$company=='A'
& malfunction$malfunction==1])
# Number of observations for company B
n2<-length(malfunction$malfunction
[malfunction$company=='B'])
# Number of successes for company A
s2<-length(malfunction$malfunction[malfunction$company=='B'
& malfunction$malfunction==1])
# Proportions
p1=s1/n1
p2=s2/n2
# Test statistic and p-value
p=(p1*n1+p2*n2)/(n1+n2)
z=(p1-p2)/sqrt((p*(1-p))*(1/n1+1/n2))
p_value=2*pnorm(-abs(z))
# Output results
z
p_value
R output
> z
[1] 2.286190
> p_value
[1] 0.02224312
Remarks:
- There is no R function to calculate this test directly.
- The data do not fulfill the criteria to ensure that the test statistic
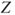 is a Gaussian distribution, because
is a Gaussian distribution, because  . In this case it is better to use Fisher's exact test, see Chapter 14.
. In this case it is better to use Fisher's exact test, see Chapter 14.
4.3 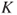 -sample tests
-sample tests
Next we present the population proportion equality test for  samples [see Bain and Engelhardt (1991) for further details]. If we have
samples [see Bain and Engelhardt (1991) for further details]. If we have  independent binomial samples we can arrange them in a
independent binomial samples we can arrange them in a  table and take advantage of results on contingency tables. We concentrate on the
table and take advantage of results on contingency tables. We concentrate on the  -test based on asymptotic results, although Fisher's exact test can be used as well. More details are given in Chapter 14.
-test based on asymptotic results, although Fisher's exact test can be used as well. More details are given in Chapter 14.
4.3.1  -sample binomial test
-sample binomial test
| Description: |
Tests if 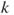 population proportions, population proportions, 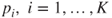 , differ from each other. , differ from each other. |
| Assumptions: |
- Data are randomly sampled with two possible outcomes.
- Let
 be denoted as “success” and be denoted as “success” and  as “failure”. as “failure”.
- The parameters
 are the proportions of success in the are the proportions of success in the  populations, populations,  . .
- Data are randomly sampled from the
 populations with sample sizes populations with sample sizes 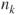 , ,  . .
- The number of successes
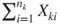 in the in the  th sample follow a binomial distribution th sample follow a binomial distribution  , ,  . .
|
| Hypothesis: |
 vs vs  for at least one for at least one 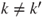 |
| Test statistic: |
 |
|
where  , , 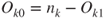 , , |
|
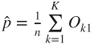 , ,  , ,  , ,  . . |
| Test decision: |
Reject 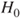 if for the observed value if for the observed value  of of  |
|
 |
| p-value: |
 |
| Annotation: |
- The test statistic
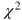 is is  -distributed. -distributed.
 is the (1- is the (1- )-quantile of the )-quantile of the  -distribution with -distribution with  degrees of freedom. degrees of freedom.- If not all expected absolute frequencies
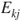 are larger or equal to are larger or equal to  , use Fisher's exact test (see Test 14.1.1). , use Fisher's exact test (see Test 14.1.1).
|
Example
The proportions of male carp in three ponds are tested for equality. The observed relative frequency of male carp in pond one is 10/19, in pond two 12/20, and in pond three 14/21.
SAS code
data counts;
input r c counts;
datalines;
1 1 10
1 0 9
2 1 12
2 0 8
3 1 14
3 0 7
;
run;
proc freq;
tables r*c /chisq;
weight counts;
run;
SAS output
Statistic DF Value Prob
Chi-Square 2 0.8187 0.6641
Remarks:
- The data step constructs a
 contingency, with r for rows (ponds 1 to 3) and c for columns (1 for male and 0 for female carp). The variable counts includes the counts for each combination between ponds and sex. In proc freq these counts can be passed by using the weight statement.
contingency, with r for rows (ponds 1 to 3) and c for columns (1 for male and 0 for female carp). The variable counts includes the counts for each combination between ponds and sex. In proc freq these counts can be passed by using the weight statement.
- With proc freq it is also possible to use raw data instead of a predefined contingency table to perform these tests. In this case there must be one variable for the ponds and one for the sex and one row for each carp. Use the same SAS statement but omit the weight command.
- Because the null hypothesis is rejected if
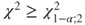 , the p-value must be calculated as 1-pchisq(0.8187,2).
, the p-value must be calculated as 1-pchisq(0.8187,2).
R code
x1 <- matrix(c(10, 12, 14, 9, 8, 7), ncol = 2)
chisq.test(x1)
R output
X-squared = 0.8187, df = 2, p-value = 0.6641
Remarks:
- The matrix command constructs a matrix
 with the ponds in the columns and the male carp population in the first row and the female carp population the second row. This matrix can then be passed on to the chisq.test function.
with the ponds in the columns and the male carp population in the first row and the female carp population the second row. This matrix can then be passed on to the chisq.test function.
- Because the null hypothesis is rejected if
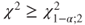 , the p-value must be calculated as 1-pchisq(0.8187,2).
, the p-value must be calculated as 1-pchisq(0.8187,2).
References
Bain L.J. and Engelhardt M. 1991 Introduction to Probability and Mathematical Statistics, 1st edn. Duxbury Press.
Keller G. and Warrack B. 1997 Statistics for Management and Economics, 4th edn. Duxbury Press.
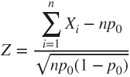
 and adding 0.5 otherwise. Omitting this option will result in a test without continuity correction.
and adding 0.5 otherwise. Omitting this option will result in a test without continuity correction.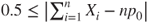 . The default value is “correct=FALSE”.
. The default value is “correct=FALSE”.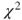 -test for one-way tables are equivalent, R uses the latter test.
-test for one-way tables are equivalent, R uses the latter test. is a Gaussian distribution, because
is a Gaussian distribution, because  , therefore the p-value is questionable.
, therefore the p-value is questionable. is a Gaussian distribution, because
is a Gaussian distribution, because  , therefore the p-value is questionable.
, therefore the p-value is questionable. is a Gaussian distribution, because
is a Gaussian distribution, because  . In this case it is better to use Fisher's exact test, see Chapter 14.
. In this case it is better to use Fisher's exact test, see Chapter 14.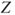 is a Gaussian distribution, because
is a Gaussian distribution, because  . In this case it is better to use Fisher's exact test, see Chapter 14.
. In this case it is better to use Fisher's exact test, see Chapter 14.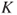 -sample tests
-sample tests![]() samples [see Bain and Engelhardt (1991) for further details]. If we have
samples [see Bain and Engelhardt (1991) for further details]. If we have ![]() independent binomial samples we can arrange them in a
independent binomial samples we can arrange them in a ![]() table and take advantage of results on contingency tables. We concentrate on the
table and take advantage of results on contingency tables. We concentrate on the ![]() -test based on asymptotic results, although Fisher's exact test can be used as well. More details are given in Chapter 14.
-test based on asymptotic results, although Fisher's exact test can be used as well. More details are given in Chapter 14. -sample binomial test
-sample binomial test contingency, with r for rows (ponds 1 to 3) and c for columns (1 for male and 0 for female carp). The variable counts includes the counts for each combination between ponds and sex. In proc freq these counts can be passed by using the weight statement.
contingency, with r for rows (ponds 1 to 3) and c for columns (1 for male and 0 for female carp). The variable counts includes the counts for each combination between ponds and sex. In proc freq these counts can be passed by using the weight statement.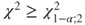 , the p-value must be calculated as 1-pchisq(0.8187,2).
, the p-value must be calculated as 1-pchisq(0.8187,2). with the ponds in the columns and the male carp population in the first row and the female carp population the second row. This matrix can then be passed on to the chisq.test function.
with the ponds in the columns and the male carp population in the first row and the female carp population the second row. This matrix can then be passed on to the chisq.test function.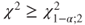 , the p-value must be calculated as 1-pchisq(0.8187,2).
, the p-value must be calculated as 1-pchisq(0.8187,2).