Chapter 14
Tests on contingency tables
In this chapter we deal with the question of whether there is an association between two random variables or not. This question can be formulated in different ways. We can ask if the two random variables are independent or test for homogeneity. The corresponding tests are presented in Section 14.1. These are foremost the well-known Fisher's exact test and Pearson's ![]() -test. In Section 14.2 we test if two raters agree on their rating of the same issue. Section 14.3 deals with two risk measures, namely the odds ratio and the relative risk.
-test. In Section 14.2 we test if two raters agree on their rating of the same issue. Section 14.3 deals with two risk measures, namely the odds ratio and the relative risk.
14.1 Tests on independence and homogeneity
In this chapter we deal with the two null hypotheses of independence and homogeneity. While a test of independence examines if there is an association between two random variables or not, a test of homogeneity tests if the marginal proportions are the same for different random variables. The test problems in this chapter can be described for the homogeneity hypothesis as well as for the independence hypothesis.
14.1.1 Fisher's exact test
| Description: | Tests the hypothesis of independence or homogeneity in a |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| with |
|
| Test statistic: | |
| Test decision: | Reject |
| (A) |
|
| or |
|
| (B) |
|
| (C) |
|
| p-values: | (A) |
| (B) |
|
| (C) |
|
with  |
|
| Annotations: |
|
proc freq data=malfunction; tables company*malfunction /fisher; run;
Fisher's Exact Test --------------------------------------- Cell (1,1) Frequency (F) 9 Left-sided Pr <= F 0.0242 Right-sided Pr >= F 0.9960 Table Probability (P) 0.0202 Two-sided Pr <= P 0.0484
- The procedure proc freq enables Fisher's exact test. After the tables statement the two variables must be specified and separated by a star (
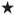 ).
). - The option fisher invokes Fisher's exact test. Alternatively the option chisq can be used, which also returns Fisher's Exact test in the case of
 tables.
tables. - Instead of using the raw data as in the example above, it is also possible to use the counts directly by constructing a
 table and handing this over to the function as first parameter:
table and handing this over to the function as first parameter:
data counts; input r c counts; datalines; 1 1 9 1 2 11 2 1 16 2 2 4 run; proc freq; tables r*c /fisher; weight counts; run;
Here the first variable r holds the first index (the rows), the second variable c holds the second index variable (the columns). The variable counts holds the frequencies for each cell. The weight command indicates the variable that holds the frequencies. - SAS arranges the factors into the
 table according to the (internal) order unless the weight method is used. The one-sided hypothesis (B) or (C) depends in their interpretation on the way data are arranged in the table, so which table is finally analyzed needs to be carefully checked.
table according to the (internal) order unless the weight method is used. The one-sided hypothesis (B) or (C) depends in their interpretation on the way data are arranged in the table, so which table is finally analyzed needs to be carefully checked.
# Read the two variables company and malfunction x<-malfunction$company y<-malfunction$malfunction # Invoke the test fisher.test(x,y,alternative="two.sided")
Fisher's Exact Test for Count Data data: x and y p-value = 0.04837
- alternative=“value” is optional and defines the type of alternative hypothesis: “two.sided”= two sided (A); “greater”=one sided (B); “less”=one sided (C). Default is “two.sided”.
-
Instead of using the raw data as in the example above, it is also possible to use the counts directly by constructing afisher.test(matrix(c(9,11,16,4), ncol = 2))
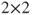 table and handing this over to the function as first parameter:
table and handing this over to the function as first parameter: - It is not clear how R arranges the factors into the
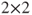 table if the “table” method is not used. For the two-sided hypothesis this does not matter, but for the directional hypotheses it is important. So in the latter case we recommend to construct a
table if the “table” method is not used. For the two-sided hypothesis this does not matter, but for the directional hypotheses it is important. So in the latter case we recommend to construct a  table and to hand this over to the function.
table and to hand this over to the function.
14.1.2 Pearson's 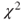 -test
-test
| Description: | Tests the hypothesis of independence or homogeneity in a two-dimensional contingency table. |
| Assumptions: |
|
| Hypotheses: | |
| vs |
|
| Test statistic: | 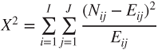 |
| with |
|
| Test decision: | Reject |
| p-values: | |
| Annotations: |
|
proc freq data=malfunction; tables company*malfunction /chisq; run;
Statistics for Table of company by malfunction Statistic DF Value Prob ------------------------------------------------------ Chi-Square 1 5.2267 0.0222 Continuity Adj. Chi-Square 1 3.8400 0.0500
- The procedure proc freq enables Pearson's
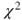 -test. Following the tables statement the two variables must be specified and separated by a star (
-test. Following the tables statement the two variables must be specified and separated by a star ( ).
). - The option chisq invokes the test.
- SAS prints the value of the test statistic and the p-value of the
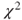 -test statistic as well as the Yates corrected
-test statistic as well as the Yates corrected  -test statistic.
-test statistic. - Instead of using the raw data, it is also possible to use the counts directly. See Test 14.1.1 for details.
# Read the two variables company and malfunction x<-malfunction$company y<-malfunction$malfunction # Invoke the test chisq.test(x,y,correct=TRUE)
Pearson's Chi-squared test with Yates' continuity correction data: x and y X-squared = 3.84, df = 1, p-value = 0.05004
- correct=“value” is optional and determines if Yates' continuity correction is used (value=TRUE) or not (value=FALSE). Default is TRUE.
- Instead of using the raw data as in the example above, it is also possible to use the counts directly by constructing a
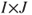 table and handing this over to the function as first parameter:
table and handing this over to the function as first parameter:
chisq.test(matrix(c(9,11,16,4), ncol = 2))
14.1.3 Likelihood-ratio  -test
-test
| Description: | Tests the hypothesis of independence or homogeneity in a two-dimensional contingency table. |
| Assumptions: |
|
| Hypotheses: | |
| vs |
|
| Test statistic: | |
| with |
|
| Test decision: | Reject |
| p-values: | |
| Annotations: |
|
proc freq data=malfunction; tables company*malfunction /chisq; run;
Statistics for Table of company by malfunction Statistic DF Value Prob ------------------------------------------------------ Likelihood Ratio Chi-Square 1 5.3834 0.0203
- The procedure proc freq enables the likelihood-ratio
 -test. Following the tables statement the two variables must be specified and separated by a star (
-test. Following the tables statement the two variables must be specified and separated by a star ( ).
). - The option chisq invokes the test.
- Instead of using the raw data, it is also possible to use the counts directly. See Test 14.1.1 for details.
# Read the two variables company and malfunction x<-malfunction$company y<-malfunction$malfunction # Get the observed and expected cases e<-chisq.test(x,y)$expected o<-chisq.test(x,y)$observed # Calculate the test statistic g2<-2*sum(o*log(o/e)) # Get degrees of freedom from function chisq.test() df<-chisq.test(x,y)$parameter # Calculate the p-value p_value=1-pchisq(g2,1) # Output results cat(“Likelihood-Ratio Chi-Square Test ”, “test statistic ”,“p-value”,“ ”, “-------------- ----------”,“ ”, “ ”,g2,“ ”,p_value,“ ”,“ ”)
Likelihood-Ratio Chi-Square Test
test statistic p-value
-------------- ----------
5.38341 0.02032911
- There is no basic R function to calculate the likelihood-ratio
 -test directly.
-test directly. - We used the R function chisq.test() to calculate the expected and observed observations as well as the degrees of freedom. See Test 14.1.2 for details on this function.
14.2 Tests on agreement and symmetry
Often categorical data are observed in so-called matched pairs, for example, as ratings of two raters on the same objects. Then it is of interest to analyze the agreement of the classification of objects into the categories. We present a test on the kappa coefficient, which is a measurement of agreement. Another question would be if the two raters classify objects into the same classes by the same proportion. For ![]() tables the McNemar test is given, in which case the hypothesis of marginal homogeneity is equivalent to that of axial symmetry.
tables the McNemar test is given, in which case the hypothesis of marginal homogeneity is equivalent to that of axial symmetry.
14.2.1 Test on Cohen's kappa
| Description: | Tests if the kappa coefficient, as measure of agreement, differs from zero. |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| where |
|
| given by |
|
| Test statistic: | |
| where |
|
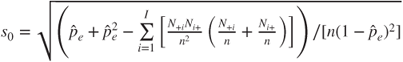 |
|
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-values: | (A) |
| (B) |
|
| (C) |
| Annotations: |
|
proc freq; tables reviewer1*reviewer2; exact kappa; run;
Simple Kappa Coefficient
--------------------------------
Kappa (K) 0.3000
ASE 0.2122
95% Lower Conf Limit -0.1160
95% Upper Conf Limit 0.7160
Test of H0: Kappa = 0
ASE under H0 0.2225
Z 1.3484
One-sided Pr> Z 0.0888
Two-sided Pr> |Z| 0.1775
Exact Test
One-sided Pr>= K 0.1849
Two-sided Pr>= |K| 0.3698
- The procedure proc freq enables this test. After the tables statement the two variables must be specified and separated by a star (
 ).
). - The option exact kappa invokes the test with asymptotic and exact p-values.
- Instead of using the raw data, it is also possible to use the counts directly. See Test 14.1.1 for details.
- Alternatively the code
proc freq data=silicosis; tables reviewer1*reviewer2 /agree; test agree; run;
can be used, but this will only give the p-values based on the Gaussian approximation. - The p-value of hypothesis (C) is not reported and must be calculated as one minus the p-value of hypothesis (B).
# Get the number of observations
n<-length(silicosis$patient)
# Construct a 2x2 table
freqtable <- table(silicosis$reviewer1,silicosis$reviewer2)
# Calculate the observed frequencies
po<-(freqtable[1,1]+freqtable[2,2])/n
# Calculate the expected frequencies
row<-margin.table(freqtable,1)/n
col<-margin.table(freqtable,2)/n
pe<-row[1]*col[1]+row[2]*col[2]
# Calculate the simple kappa coefficient
k<-(po-pe)/(1-pe)
# Calculate the variance under the null hypothesis
var0<-( pe+pe∧2 - (row[1]*col[1]*(row[1]+col[1])+
row[2]*col[2]*(row[2]+col[2])))
/(n*(1-pe)∧2)
# Calculate the test statistic
z<-k/sqrt(var0)
# Calculate p_values
p_value_A<-2*pnorm(-abs(z))
p_value_B<-1-pnorm(z)
p_value_C<-pnorm(z)
# Output results
k
z
p_value_A
p_value_B
p_value_C
> k 0.3 > z 1.3484 > p_value_A 0.1775299 > p_value_B 0.08876493 > p_value_C 0.9112351
- There is no basic R function to calculate the test directly.
- The R function table is used to construct the basic
 table and the R function margin.table is used to get the marginal frequencies of this table.
table and the R function margin.table is used to get the marginal frequencies of this table.
14.2.2 McNemar's test
| Description: | Test on axial symmetry or marginal homogeneity in a |
| Assumptions: |
|
| Hypotheses: | |
| with |
|
| Test statistic: |
| Test decision: | Reject |
| p-values: | |
| Annotations: |
|
* Dichotomize the variables iq1 and iq2; data temp; set iq; if iq1<=100 then iq_before=0; if iq1> 100 then iq_before=1; if iq2<=100 then iq_after=0; if iq2> 100 then iq_after=1; run; * Apply the test; proc freq; tables iq_before*iq_after; exact mcnem; run;
Statistics for Table of iq_before by iq_after
McNemar's Test
----------------------------
Statistic (S) 6.0000
DF 1
Asymptotic Pr > S 0.0143
Exact Pr >= S 0.0313
- The procedure proc freq enables this test. After the tables statement the two variables must be specified and separated by a star (
 ).
). - The option exact mcnem invokes the test with asymptotic and exact p-values.
- Instead of using the raw data, it is also possible to use the counts directly. See Test 14.1.1 for details.
- SAS does not provide a continuity correction.
# Dichotomize the variables IQ1 and IQ2 iq_before <- ifelse(iq$IQ1<=100, 0, 1) iq_after <- ifelse(iq$IQ2<=100, 0, 1) # Apply the test mcnemar.test(iq_before, iq_after, correct = FALSE)
McNemar's Chi-squared test data: iq_before and iq_after McNemar's chi-squared = 6, df = 1, p-value = 0.01431
- correct=“value” is optional and determines if a continuity correction is used (value=TRUE) or not (value=FALSE). Default is TRUE.
- Instead of using the raw data as in the example above, it is also possible to use the counts directly by constructing the
 table and handing this over to the function as first parameter:
table and handing this over to the function as first parameter:
freqtable<-table(iq_before, iq_after) mcnemar.test(freqtable, correct = FALSE)
14.2.3 Bowker's test for symmetry
| Description: | Test on symmetry in a |
| Assumptions: |
|
| Hypotheses: | |
| vs |
|
| with |
|
| Test statistic: |  |
| Test decision: | Reject |
| p-values: | |
| Annotations: |
|
* Construct the contingency table; data counts; input gp1 gp2 counts; datalines; 1 1 10 1 2 8 1 3 12 2 1 13 2 2 14 2 3 6 3 1 1 3 2 10 3 3 20 run; * Apply the test; proc freq; tables gp1*gp2; weight counts; exact agree; run;
Statistics for Table of gp1 by gp2
Test of Symmetry
------------------------
Statistic (S) 11.4982
DF 3
Pr> S 0.0093
- The procedure proc freq enables this test. After the tables statement the two variables must be specified and separated by a star (
 ).
). - The first variable gp1 holds the rating index of the first physician, and the second variable gp2 the rating index of the second physician. The variable counts hold the frequency for each cell of the contingency table.
- The option exact agree invokes Bowker's test if applied to tables larger than
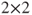 , stating asymptotic and exact p-values.
, stating asymptotic and exact p-values. - It is also possible to use raw data, see Test 14.1.1 for details.
- SAS does not provide a continuity correction.
# Construct the contingency table table<-matrix(c(10,13,1,8,14,10,12,6,20),ncol=3) # Apply the test mcnemar.test(table)
McNemar's Chi-squared test data: table McNemar's chi-squared = 11.4982, df = 3, p-value = 0.009316
- R uses the function mcnemar.test to apply Bowker's test for symmetry, but a continuity correction is not provided.
- It is also possible to use raw data, see Test 14.1.1 for details.
14.3 Test on risk measures
In this section we introduce tests for two common risk measures in ![]() tables. The odds ratio and the relative risks are mainly used in epidemiology to identify risk factors for an health outcome. Note, for risk estimates a confidence interval is in most cases more meaningful than a test, because the confidence interval reflects the variability of an estimator.
tables. The odds ratio and the relative risks are mainly used in epidemiology to identify risk factors for an health outcome. Note, for risk estimates a confidence interval is in most cases more meaningful than a test, because the confidence interval reflects the variability of an estimator.
14.3.1 Large sample test on the odds ratio
| Description: | Tests if the odds ratio in a |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| where |
| Test statistic: | |
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-values: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
* Sort the dataset in the right order;
proc sort data=malfunction;
by company descending malfunction;
run;
* Use proc freq to get the counts saved into freq_table;
proc freq order=data;
tables company*malfunction /out=freq_table;
run;
* Get the counts out of freq_table;
data n11 n12 n21 n22;
set freq_table;
if company='A' and malfunction=1 then do;
keep count; output n11;
end;
if company='A' and malfunction=0 then do;
keep count; output n12;
end;
if company='B' and malfunction=1 then do;
keep count; output n21;
end;
if company='B' and malfunction=0 then do;
keep count; output n22;
end;
run;
* Rename counts;
data n11; set n11; rename count=n11; run;
data n12; set n12; rename count=n12; run;
data n21; set n21; rename count=n21; run;
data n22; set n22; rename count=n22; run;
* Merge counts together and calculate test statistic;
data or_table;
merge n11 n12 n21 n22;
* Calculate the Odds Ratio;
OR=(n11*n22)/(n12*n21);
* Calculate the standard deviation of ln(OR);
SD=sqrt(1/n11+1/n12+1/n22+1/n21);
* Calculate test statistic;
z=log(OR)/SD;
* Calculate p-values;
p_value_A=2*probnorm(-abs(z));
p_value_B=1-probnorm(z);
p_value_C=probnorm(z);
run;
* Output results;
proc print split='*' noobs;
var OR z p_value_A p_value_B p_value_C;
label OR='Odds Ratio*----------'
z='Test Statistic*--------------'
p_value_A='p-value A*---------'
p_value_B='p-value B*---------'
p_value_C='p-value C*---------';
title 'Test on the Odds Ratio';
run;
Test on the Odds Ratio Odds Ratio Test Statistic p-value A p-value B ---------- -------------- --------- --------- 4.88889 2.21241 0.026938 0.013469 p-value C --------- 0.98653
- The above code calculates the odds ratio for the malfunctions of company A vs B. An odds ratio of
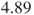 means that a malfunction in company A is
means that a malfunction in company A is  times more likely than in company B. Changing the rows of the table results in an estimated odds ratio of
times more likely than in company B. Changing the rows of the table results in an estimated odds ratio of  , which means that a malfunction in company B is
, which means that a malfunction in company B is 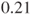 less likely than in company A.
less likely than in company A. - There is no generic SAS function to calculate the p-value in a
 table directly, but logistic regression can be used as in the following code:
table directly, but logistic regression can be used as in the following code:
proc logistic data=malfunction; class company (PARAM=REF REF='B'), model malfunction (event='1') = company; run;
Note, this code correctly returns the above two-sided p-value and also the odds ratio of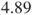 , because with the code class company (PARAM=REF REF='B'), we tell SAS to use company B as reference. One-sided p-values are not given.
, because with the code class company (PARAM=REF REF='B'), we tell SAS to use company B as reference. One-sided p-values are not given. - Also with proc freq the odds ratio itself can be calculated.
* Sort the dataset in the right order; proc sort data=malfunction; by company descending malfunction; run; * Apply the test; proc freq order=data; tables company*malfunction /relrisk; exact comor; run;
However, no p-values are reported.
# Get the cell counts for the 2x2 table
n11<-sum(malfunction$company=='A' &
malfunction$malfunction==1)
n12<-sum(malfunction$company=='A' &
malfunction$malfunction==0)
n21<-sum(malfunction$company=='B' &
malfunction$malfunction==1)
n22<-sum(malfunction$company=='B' &
malfunction$malfunction==0)
# Calculate the Odds Ratio
OR=(n11*n22)/(n12*n21)
# Calculate the standard deviation of ln(OR)
SD=sqrt(1/n11+1/n12+1/n22+1/n21)
# Calculate test statistic
z=log(OR)/SD
# Calculate p-values
p_value_A<-2*pnorm(-abs(z));
p_value_B<-1-pnorm(z);
p_value_C<-pnorm(z);
# Output results
OR
z
p_value_A
p_value_B
p_value_C
> OR [1] 4.888889 > z [1] 2.212413 > p_value_A [1] 0.02693816 > p_value_B [1] 0.01346908 > p_value_C [1] 0.986531
- The above code calculates the odds ratio for the malfunctions of company A vs B. An odds ratio of
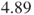 means that a malfunction in company A is
means that a malfunction in company A is  times more likely than in company B. Changing the rows in the table results in an odds ratio of
times more likely than in company B. Changing the rows in the table results in an odds ratio of  and means that a malfunction in company B is
and means that a malfunction in company B is 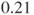 less likely than in company A.
less likely than in company A. - There is no generic R function to calculate the odds ratio in a
 table, but logistic regression can be used as in the following code:
table, but logistic regression can be used as in the following code:
x<-malfunction$company y<-malfunction$malfunction summary(glm(x∼y,family=binomial(link=“logit”)))
Note, this code correctly returns the above two-sided p-value, but not the odds ratio of , due to the used specification of which factors enter the regression in which order. Here, R returns a log(odds ratio) of
, due to the used specification of which factors enter the regression in which order. Here, R returns a log(odds ratio) of  which equals an odds ratio of
which equals an odds ratio of 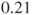 (see first remark). One-sided p-values are not given.
(see first remark). One-sided p-values are not given.
14.3.2 Large sample test on the relative risk
| Description: | Tests if the relative risk in a |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| with |
|
| Test statistic: | |
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-values: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
|
* Sort the dataset in the right order;
proc sort data=malfunction;
by company descending malfunction;
run;
* Use proc freq to get the counts saved into freq_table;
proc freq order=data;
tables company*malfunction /out=freq_table;
run;
* Get the counts out of freq_table;
data n11 n12 n21 n22;
set freq_table;
if company='A' and malfunction=1 then do;
keep count; output n11;
end;
if company='A' and malfunction=0 then do;
keep count; output n12;
end;
if company='B' and malfunction=1 then do;
keep count; output n21;
end;
if company='B' and malfunction=0 then do;
keep count; output n22;
end;
run;
* Rename counts;
data n11; set n11; rename count=n11; run;
data n12; set n12; rename count=n12; run;
data n21; set n21; rename count=n21; run;
data n22; set n22; rename count=n22; run;
* Merge counts and calculate test statistic;
data rr_table;
merge n11 n12 n21 n22;
* Calculate the Relative Risk;
RR=(n11/(n11+n12))/(n21/(n21+n22));
* Calculate the standard deviation of ln(RR);
SD=sqrt(1/n11-1/(n11+n12)+1/n21-1/(n21+n22));
* Calculate test statistic;
z=log(RR)/SD;
* Calculate p-values;
p_value_A=2*probnorm(-abs(z));
p_value_B=1-probnorm(z);
p_value_C=probnorm(z);
run;
* Output results;
proc print split='*' noobs;
var RR z p_value_A p_value_B p_value_C;
label RR='Relative Risk*-------------'
z='Test Statistic*--------------'
p_value_A='p-value A*---------'
p_value_B='p-value B*---------'
p_value_C='p-value C*---------';
title 'Test on the Relative Risk';
run;
Test on the Relative Risk
Relative Risk Test Statistic p-value A p-value B
------------- -------------- --------- ---------
2.75 2.06102 0.039301 0.019650
p-value C
---------
0.98035
- The above code calculates the relative risk of malfunctions in products from company A vs B. The risk is
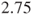 times higher in company A than in company B. Changing the rows of the table results in an estimated relative risk of
times higher in company A than in company B. Changing the rows of the table results in an estimated relative risk of  and means that a malfunction in a product from company B is
and means that a malfunction in a product from company B is  times less likely than from company A.
times less likely than from company A. - There is no generic SAS function to calculate the p-values of a relative risk ratio in a
 table, but generalized linear models can be used as in the following code:
table, but generalized linear models can be used as in the following code:
proc genmod data = malfunction descending; class company (PARAM=REF REF='B'), model malfunction=company /dist=binomial link=log; run;
Note, this code correctly returns the above two-sided p-value and also the relative risk of , as with the code class company (PARAM=REF REF='B') we tell SAS to use company B as reference. SAS returns here a log(relative risk) of
, as with the code class company (PARAM=REF REF='B') we tell SAS to use company B as reference. SAS returns here a log(relative risk) of  which equals a relative risk of
which equals a relative risk of  (see first remark). One-sided p-values are not given.
(see first remark). One-sided p-values are not given. - However, with proc freq the relative risk itself can be calculated but not the p-values:
* Sort the dataset in the right order; proc sort data=malfunction; by company descending malfunction; run; * Apply the test; proc freq order=data; tables company*malfunction /relrisk; run;
In the output the Cohort (Col1 Risk) states our wanted relative risk estimate as we are interested in the risk between row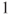 and row
and row  .
.
# Get the cell counts for the 2x2 table
n11<-sum(malfunction$company=='A' &
malfunction$malfunction==1)
n12<-sum(malfunction$company=='A' &
malfunction$malfunction==0)
n21<-sum(malfunction$company=='B' &
malfunction$malfunction==1)
n22<-sum(malfunction$company=='B' &
malfunction$malfunction==0)
# Calculate the Relative Risk
RR=(n11/(n11+n12))/(n21/(n21+n22))
# Calculate the standard deviation of ln(RR)
SD=sqrt(1/n11-1/(n11+n12)+1/n21-1/(n21+n22))
# Calculate test statistic
z=log(RR)/SD
# Calculate p-values
p_value_A<-2*pnorm(-abs(z));
p_value_B<-1-pnorm(z);
p_value_C<-pnorm(z);
# Output results
RR
z
p_value_A
p_value_B
p_value_C
> RR [1] 2.75 > z [1] 2.061022 > p_value_A [1] 0.03930095 > p_value_B [1] 0.01965047 > p_value_C [1] 0.9803495
- The above code calculates the relative risk of malfunctions in products from company A vs B. The risk of a malfunction in a product is
 times higher in company A than in company B. Changing the rows in the table results in an estimated relative risk of
times higher in company A than in company B. Changing the rows in the table results in an estimated relative risk of 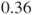 and means that a malfunction in a product from company B is
and means that a malfunction in a product from company B is 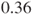 times less likely than from company A.
times less likely than from company A. - There is no generic R function to calculate the relative risk ratio in a
 table, but generalized linear models can be used. The following code will do that:
table, but generalized linear models can be used. The following code will do that:
x<-malfunction$company y<-malfunction$malfunction summary(glm(y∼x,family=binomial(link=“logit”)))
Note, this code correctly returns the above two-sided p-value, but not the relative risk of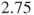 , due to the used specification of which factors enter the regression in which order. Here, R returns a log(relative risk) of
, due to the used specification of which factors enter the regression in which order. Here, R returns a log(relative risk) of 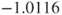 which equals a relative risk of
which equals a relative risk of 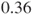 (see first remark). One-sided p-values are not given.
(see first remark). One-sided p-values are not given.
References
Agresti A. 1990 Categorical Data Analysis. John Wiley & Sons, Ltd.
Bowker A.H. 1948 A test for symmetry in contingency tables. Journal of the American Statistical Associtaion 43, 572–574.
Cohen J. 1960 A coefficient of agreement for nominal scales. Educational and Psychological Measurement 10, 37–46.
Cornfield J. 1951 A method of estimation comparative rates from clinical data. Applications to cancer of the lung, breast and cervix. Journal of the National Cancer Institute 11, 1229–1275.
Edwards A.L. 1948. Note on the correction for continuity in testing the significance of the difference between correlated proportions. Psychometrika 13, 185–187.
Fisher R.A. 1922 On the interpretation of chi-square from contingency tables, and the calculation of P. Journal of the Royal Statistical Society 85, 87–94.
Fisher R.A. 1934 Statistical Methods for Research Workers, 5th edn. Oliver & Boyd.
Fisher R.A. 1935 The logic of inductive inference. Journal of the Royal Statistical Society, Series A 98, 39–54.
Fleiss J.L., Levin B. and Paik M.C. 2003 Statistical Methods for Rates and Proportions, 3rd edn. John Wiley & Sons, Ltd.
Freeman G.H. and Halton J.H. 1951 Note on an exact treatment of contingency, goodness of fit and other problems of significance. Biometrika 38, 141–149.
Irwin J.O. 1935 Tests of significance for differences between percentages based on small numbers. Metron 12, 83–94.
Krampe A. and Kuhnt S. 2007 Bowker's test for symmetry and modifications within the algebraic framework. Computational Statistics & Data Analysis 51, 4124–4142.
McNemar Q. 1947 Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 12, 153–157.
Pearson K. 1900 On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophical Magazine 50, 157–175.
Yates F. 1934 Contingency tables involving small numbers and the ![]() test. Journal of the Royal Statistical Society Supplement 34, 217–235.
test. Journal of the Royal Statistical Society Supplement 34, 217–235.

 . Given the marginal totals,
. Given the marginal totals,  .
.