Chapter 9
Tests on scale difference
In this chapter we present nonparametric tests for the scale parameter. Actually, it is tested if two samples come from the same population where alternatives are characterized by differences in dispersion. These tests are called tests on the scale, spread or dispersion. The most famous one is the Siegel–Tukey test (Test 9.1.1). The introduced tests can be employed if the samples are not normally distributed, but the equality of median assumption is crucial.
9.1 Two-sample tests
9.1.1 Siegel–Tukey test
| Description: | Tests if the scale (variance) of two independent populations is the same. |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| Test statistic: | For |
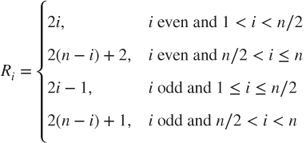
If ![]() is uneven, the above ranking is applied after the middle observation of the combined and ordered sample is discarded and the sample size is reduced to
is uneven, the above ranking is applied after the middle observation of the combined and ordered sample is discarded and the sample size is reduced to ![]() .
.
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
proc npar1way data=blood_pressure correct=no st; var mmhg; class status; exact st; run;
The NPAR1WAY Procedure
Siegel–Tukey Scores for Variable mmhg
Classified by Variable status
Sum of Expected Std Dev Mean
status N Scores Under H0 Under H0 Score
-------------------------------------------------------
0 25 655.0 700.0 59.001584 26.20
1 30 885.0 840.0 59.001584 29.50
Average scores were used for ties.
Siegel–Tukey Two-Sample Test
Statistic 655.0000
Z −0.7627
One-Sided Pr < Z 0.2228
Two-Sided Pr > |Z| 0.4456
- The parameter st enables the Siegel–Tukey test of the procedure NPAR1WAY.
- correct=value is optional. If value is YES than a continuity correction for the normal approximation is used. The default is NO.
- exact st is optional and applies an additional exact test. Note, the computation of an exact test can be very time consuming. This is the reason why in this example no exact p-values are given in the output.
- Besides the two-sided p-value SAS also reports a one-sided p-value; which one is printed depends on the Z-statistic. If it is greater than zero the right-sided p-value is printed. If it is less than or equal to zero the left-sided p-value is printed.
- In this example the sum of scores for the healthy subjects is 655.0 compared with 885.0 for the people with hypertension. So there is evidence that the scale of healthy subjects is higher than the scale of unhealthy subjects. In fact the variance of the healthy subjects is 124.41 and the variance of the unhealthy subjects is 120.05. Therefore the p-value for hypothesis (C) is
 and the p-value for hypothesis (B) is
and the p-value for hypothesis (B) is  .
. - In the case of odd sample sizes SAS does not delete the middle observation.
# Helper functions to find even or odd numbers
is.even <- function(x) x %% 2 == 0
is.odd <- function(x) x %% 2 == 1
# Create a sorted matrix with first column the blood
# pressure and second column the status
data<-blood_pressure[order(blood_pressure$mmhg),]
x<-c(data$mmhg)
x<-cbind(x,data$status)
# If the sample size is odd then remove the observation
# in the middle
if (is.odd(nrow(x))) x<-x[-c(nrow(x)/2+0.5),]
# Calculate the (remaining) sample size
n<-nrow(x)
# y returns the Siegel–Tukey scores
y<-rep(0,times=n)
# Assigning the scores
for (i in seq(along=x)) {
if (1<i & i <= n/2 & is.even(i))
{
y[i]<-2*i
}
else if (n/2<i & i<=n & is.even(i))
{
y[i]<-2*(n-i)+2
}
else if (1<=i & i <=n/2 & is.odd(i))
{
y[i]<-2*i-1
}
else if (n/2<i & i < n & is.odd(i))
{
y[i]<-2*(n-i)+1
}
}
# Now mean scores must be created if necessary
t<-tapply(y,x[,1],mean) # Get mean scores for tied values
v<-strsplit(names(t), “ ”) # Get mmhg values
# r
r<-rep(0,times=n)
# Assign ranks and mean ranks to r
for (i in seq(along=r))
{
for (j in seq(along=v))
{
if (x[i,1]==as.numeric(v[j])) r[i]=t[j]
}
}
# Now calculate the test statistics S_0 (status 0)
# and S_1 (status 1) for both samples
S_0<-0
S_1<-0
for (i in seq(along=r)) {
if(x[i,2]==0) S_0=S_0+r[i]
if(x[i,2]==1) S_1=S_1+r[i]
}
# Calculate sample sizes for status=0 and status=1
n1<-sum(x[,2]==0)
n2<-sum(x[,2]==1)
# Choose the test statistic which belongs to the smallest
# sample size
if (n1<=n2) {
# Choose the smaller |z| value
z1<-(2*S_0-n1*(n+1)+1)/sqrt((n1*n2*(n+1)/3))
z2<-(2*S_0-n1*(n+1)-1)/sqrt((n1*n2*(n+1)/3))
if (abs(z1)<=abs(z2)) z=z1 else z=z2
pvalue_B=1-pnorm(-abs(z))
pvalue_C=pnorm(-abs(z))
}
if (n1>n2) {
# Choose the smaller |z| value
z1<-(2*S_1-n2*(n+1)+1)/sqrt((n1*n2*(n+1)/3))
z2<-(2*S_1-n2*(n+1)-1)/sqrt((n1*n2*(n+1)/3))
if (abs(z1)<=abs(z2)) z=z1 else z=z2
pvalue_B=pnorm(-abs(z));
pvalue_C=1-pnorm(-abs(z));
}
pvalue_A=2*min(pnorm(-abs(z)),1-pnorm(-abs(z)));
# Output results
print(“Siegel–Tukey test”)
n
S_0
S_1
z
pvalue_A
pvalue_B
pvalue_C
[1] “Siegel–Tukey test” > n [1] 54 > S_0 [1] 600.5 > S_1 [1] 884.5 > z [1] -1.027058 > pvalue_A [1] 0.3043931 > pvalue_B [1] 0.8478035 > pvalue_C [1] 0.1521965
- There is no basic R function to calculate this test directly.
- In this implementation of the test, the observation in the middle of the sorted sample is removed. This is different to SAS and therefore the calculated values of the test statistic are not the same.
- In the case of ties–as in the above sample–the construction of ranks must be made in two passes. First the ranks are constructed in the ordered combined sample. Afterwards the mean of ranks of the tied observations are calculated.
9.1.2 Ansari–Bradley test
| Description: | Tests if the scale (variance) of two independent populations is the same. |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| Test statistic: | For |

| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
proc npar1way data=blood_pressure correct=no ab; var mmhg; class status; exact ab; run;
The NPAR1WAY Procedure
Ansari–Bradley Scores for Variable mmhg
Classified by Variable status
Sum of Expected Std Dev Mean
status N Scores Under H0 Under H0 Score Score
----------------------------------------------------------
0 25 334.0 356.363636 29.533137 13.360 13.360
1 30 450.0 427.636364 29.533137 15.000 15.000
Average scores were used for ties.
Ansari–Bradley Two-Sample Test
Statistic 334.0000
Z -0.7572
One-Sided Pr < Z 0.2245
Two-Sided Pr < |Z| 0.4489
- The parameter ab enables the Ansari–Bradley test of the procedure NPAR1WAY.
- correct=value is optional. If value is YES than a continuity correction for the normal approximation is used. The default is NO.
- exact ab is optional and applies an additional exact test. Note, the computation of an exact test can be very time consuming. This is the reason why in this example no exact p-values are given in the output.
- Besides the two-sided p-value SAS also reports a one-sided p-value; which one is printed depends on the Z-statistic. If the value of the Z-statistic is greater than zero the right-sided p-value is printed. If it is less than or equal to zero the left-sided p-value is printed.
- In this example the sum of scores for the healthy subjects is
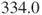 compared with
compared with  for the people with hypertension. So there is evidence that the scale of healthy subjects is higher than the scale of unhealthy subjects. In fact the variance of the healthy subjects is
for the people with hypertension. So there is evidence that the scale of healthy subjects is higher than the scale of unhealthy subjects. In fact the variance of the healthy subjects is  and the variance of the unhealthy subjects is
and the variance of the unhealthy subjects is 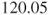 . Therefore the p-value for hypothesis (C) is
. Therefore the p-value for hypothesis (C) is 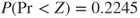 and the p-value for hypothesis (B) is
and the p-value for hypothesis (B) is 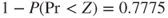 .
.
x<-blood_pressure$mmhg[blood_pressure$status==0] y<-blood_pressure$mmhg[blood_pressure$status==1] ansari.test(x,y,exact=NULL,alternative =“two.sided”)
Ansari–Bradley test
data: x and y
AB = 334, p-value = 0.4489
alternative hypothesis: true ratio of scales is not
equal to 1
- exact=value is optional. If value is not specified or TRUE an exact p-value is computed if the combined sample size is less than
 . If it is NULL or FALSE the approximative p-value is computed. In the case of ties R cannot compute an exact test.
. If it is NULL or FALSE the approximative p-value is computed. In the case of ties R cannot compute an exact test. - R tests equivalent hypotheses of the type
 vs
vs  for hypothesis (A), and so on.
for hypothesis (A), and so on. - alternative=“value” is optional and defines the type of alternative hypothesis: “two.sided”= true ratio of scales is not equal to 1 (A); “greater”=true ratio of scales is greater than 1 (C); “lower”=true ratio of scales is less than 1 (B). Default is “two.sided”.
9.1.3 Mood test
| Description: | Tests if the scale (variance) of two independent populations is the same. |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
| Test statistic: | For |
| where |
|
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
proc npar1way data=blood_pressure correct=no mood; var mmhg; class status; exact mood; run;
The NPAR1WAY Procedure
Mood Scores for Variable mmhg
Classified by Variable status
Sum of Expected Std Dev Mean
status N Scores Under H0 Under H0 Score
----------------------------------------------------------
0 25 6864.0 6300.0 837.786511 274.560
1 30 6996.0 7560.0 837.786511 233.200
Average scores were used for ties.
Mood Two-Sample Test
Statistic 6864.0000
Z 0.6732
One-Sided Pr> Z 0.2504
Two-Sided Pr> |Z| 0.5008
- The parameter mood enables the Mood test of the procedure NPAR1WAY.
- correct=value is optional. If value is YES than a continuity correction for the normal approximation is used. The default is NO.
- exact mood is optional and applies an additional exact test. Note, the computation of an exact test can be very time consuming. This is the reason why in this example no exact p-values are given in the output.
- Besides the two-sided p-value SAS also reports a one-sided p-value; which one is printed depends on the Z-statistic. If the observed value of the Z-statistic is greater than zero the right-sided p-value is printed. If it is less than or equal to zero the left-sided p-value is printed.
- In this example the sum of scores for the healthy subjects is
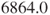 compared with
compared with 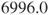 for the people with hypertension. So there is evidence that the scale of healthy subjects is higher than the scale of unhealthy subjects. In fact the variance of the healthy subjects is
for the people with hypertension. So there is evidence that the scale of healthy subjects is higher than the scale of unhealthy subjects. In fact the variance of the healthy subjects is 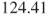 and the variance of the unhealthy subjects is
and the variance of the unhealthy subjects is  . Therefore the p-value for hypothesis (C) is
. Therefore the p-value for hypothesis (C) is 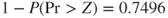 and the p-value for hypothesis (B) is
and the p-value for hypothesis (B) is 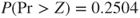 .
.
x<-blood_pressure$mmhg[blood_pressure$status==0] y<-blood_pressure$mmhg[blood_pressure$status==1] mood.test(x,y,alternative =“two.sided”)
Mood two-sample test of scale data: x and y Z = 0.6765, p-value = 0.4987 alternative hypothesis: two.sided
- R handles ties differently to SAS. Instead of mid ranks a procedure by Mielke is used (Mielke 1967).
- alternative=“value” is optional and defines the type of alternative hypothesis: “two.sided”= true ratio of scales is not equal to 1 (A); “greater”=true ratio of scales is greater than 1 (C); “lower”=true ratio of scales is less than 1 (B). Default is “two.sided”.
References
Ansari A.R. and Bradley R.A. 1960 Rank-sum tests for disperson. Annals of Mathematical Statistics 31, 1174–1189.
Hollander M. and Wolfe D.A. 1999 Nonparametric Statistical Methods, 2nd edn. John Wiley & Sons, Ltd.
Laubscher N.F., Steffens F.E. and DeLange E.M. 1968 Exact critical values for Mood's distribution-free test statistic for dispersion and its normal approximation. Technometrics 10, 497–508.
Mielke P.W. 1967 Note on some squared rank tests with existing ties. Technometrics 9, 312–314.
Mood A.M. 1954 On the asymptotic efficiency of certain nonparametric two-sample tests. Annals of Mathematical Statistics 25, 514–522.
Siegel S. and Tukey J.W. 1980 A nonparametric sum of ranks procedure for relative spread in unpaired samples. Journal of the American Statistical Association 55, 429–445.
