Chapter 3
Tests on the variance
This chapter contains statistical tests on the variance of normal populations. In the one-sample case it is of interest whether the variance of a single population differs from some pre-specified value, where the mean value of the underlying Gaussian distribution may be known or unknown. SAS and R do not provide the user with ready to use procedures or functions for the resulting ![]() -tests. For the two-sample cases it must be distinguished between independent and dependent samples. In the former case an F-test and in the latter case a t-test is appropriate. The SAS procedure proc ttest provides a way to calculate the test for the two-sided hypothesis. We additionally show how the test can be performed for the one-sided hypothesis. In R the function var.test calculates the test for all hypotheses. In SAS and R there is no convenient way to calculate the t-test for dependent samples and we provide code for it. For k-sample variance tests (Levene test, Bartlett test) please refer to Chapter 17 which covers ANOVA tests.
-tests. For the two-sample cases it must be distinguished between independent and dependent samples. In the former case an F-test and in the latter case a t-test is appropriate. The SAS procedure proc ttest provides a way to calculate the test for the two-sided hypothesis. We additionally show how the test can be performed for the one-sided hypothesis. In R the function var.test calculates the test for all hypotheses. In SAS and R there is no convenient way to calculate the t-test for dependent samples and we provide code for it. For k-sample variance tests (Levene test, Bartlett test) please refer to Chapter 17 which covers ANOVA tests.
3.1 One-sample tests
This section deals with the question, if the variance differs from a predefined value.
3.1.1 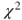 -test on the variance (mean known)
-test on the variance (mean known)
| Description: | Tests if a population variance |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
| Test statistic: | |
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
*Calculate squared sum; data chi01; set blood_pressure; mean0=130; * Set the known mean; square_diff=(mmhg-mean0)**2; run; proc summary; var square_diff; output out=chi02 sum=sum_square_diff; run; * Calculate test-statistic and p-values; data chi03; set chi02; format p_value_A p_value_B p_value_C pvalue.; df=_FREQ_; sigma0=20; * Set std under the null hypothesis; chisq=sum_square_diff/(sigma0**2); * p-value for hypothesis (A); p_value_A=2*min(probchi(chisq,df),1-probchi(chisq,df)); * p-value for hypothesis (B); p_value_B=1-probchi(chisq,df); * p-value for hypothesis (C); p_value_C=probchi(chisq,df); run; * Output results; proc print; var chisq df p_value_A p_value_B p_value_c; run;
chisq df p_value_A p_value_B p_value_C 49.595 55 0.6390 0.6805 0.3195
- There is no SAS procedure to calculate this
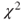 -test directly.
-test directly.
mean0<-130 # Set known mean sigma0<-20 # Set std under the null hypothesis # Calculate squared sum; sum_squared_diff<-sum((blood_pressure$mmhg-mean0)∧2) # Calculate test-statistic and p-values; df<-length(blood_pressure$mmhg) chisq<-sum_squared_diff/(sigma0∧2) # p-value for hypothesis (A) p_value_A=2*min(pchisq(chisq,df),1-pchisq(chisq,df)) # p-value for hypothesis (B) p_value_B=1-pchisq(chisq,df) # p-value for hypothesis (C) p_value_C=pchisq(chisq,df) # Output results chisq df p_value_A p_value_B p_value_C
> chisq [1] 49.595 > df [1] 55 > p_value_A [1] 0.6389885 > p_value_B [1] 0.6805057 > p_value_C [1] 0.3194943
- There is no basic R function to calculate this
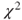 -test directly.
-test directly.
3.1.2 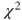 -test on the variance (mean unknown)
-test on the variance (mean unknown)
| Description: | Tests if a population variance |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| Test statistic: | |
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
* Calculate sample std and sample size; proc means data=blood_pressure std; var mmhg; output out=chi01 std=std_sample n=n_total; run; * Calculate test-statistic and p-values; data chi02; set chi01; format p_value_A p_value_B p_value_C pvalue.; df=n_total-1; sigma0=20; * Set std under the null hypothesis; chisq=(df*(std_sample**2))/(sigma0**2); * p-value for hypothesis (A); p_value_A=2*min(probchi(chisq,df),1-probchi(chisq,df)); * p-value for hypothesis (B); p_value_B=1-probchi(chisq,df); * p-value for hypothesis (C); p_value_C=probchi(chisq,df); run; * Output results; proc print; var chisq df p_value_A p_value_B p_value_c; run;
chisq df p_value_A p_value_B p_value_C 49.595 54 0.71039 0.64480 0.35520
- There is no SAS procedure to calculate this
 -test directly.
-test directly.
# Calculate sample std and sample size; std_sample<-sd(blood_pressure$mmhg) n<-length(blood_pressure$mmhg) # Set std under the null hypothesis sigma0<-20 # Calculate test-statistic and p-values; df=n-1 chisq<-(df*std_sample∧2)/(sigma0∧2) # p-value for hypothesis (A) p_value_A=2*min(pchisq(chisq,df),1-pchisq(chisq,df)) # p-value for hypothesis (B) p_value_B=1-pchisq(chisq,df) # p-value for hypothesis (C) p_value_C=pchisq(chisq,df) # Output results chisq df p_value_A p_value_B p_value_C
> chisq [1] 49.595 > df [1] 54 > p_value_A [1] 0.7103942 > p_value_B [1] 0.6448029 > p_value_C [1] 0.3551971
- There is no basic R function to calculate this
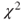 -test directly.
-test directly.
3.2 Two-sample tests
This section covers two-sample tests, which enable us to test if the variances of two populations differ from each other.
3.2.1 Two-sample  -test on variances of two populations
-test on variances of two populations
| Description: | Tests if two population variances |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| Test statistic: |
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
*** Variant 1 ***;
* Only for hypothesis (A);
proc ttest data=blood_pressure h0=0 sides=2;
class status;
var mmhg;
run;
*** Variant 2 ***;
* For hypotheses (A),(B), and (C);
* Calculate the two standard deviations and;
* sample size;
proc means data=blood_pressure std;
var mmhg;
by status;
output out=ftest01 std=stdvalue n=n_total;
run;
* Output the std in two different datasets;
data ftest02 ftest03;
set ftest01;
if status=0 then output ftest02;
if status=1 then output ftest03;
run;
* Rename std and sample size of the subjects with;
* status=0;
data ftest02;
set ftest02;
rename stdvalue=std_status0
n_total=n_status0;
run;
* Rename std and sample size of subjects with;
* status=1;
data ftest03;
set ftest03;
rename stdvalue=std_status1
n_total=n_status1;
run;
* Calculate test statistic p-values;
data ftest04;
merge ftest02 ftest03;
format p_value_A p_value_B p_value_C pvalue.;
* Calculate numerator and denominator of the;
* F-statistic;
std_num=max(std_status0,std_status1);
std_den=min(std_status0,std_status1);
* Calculate the appropriate degrees of freedom;
if std_num=std_status0 then
do;
df_num=n_status0-1;
df_den=n_status1-1;
end;
else
do;
df_num=n_status1-1;
df_den=n_status0-1;
end;
* Calculate the test-statistic;
f=std_num**2/std_den**2;
* p-value for hypothesis (A);
p_value_A=2*min(probf(f,df_num,df_den),
1-probf(f,df_num,df_den));
* p-value for hypothesis (B);
p_value_B=1-probf(f,df_num,df_den);
* p-value for hypothesis (C);
p_value_C=probf(f,df_num,df_den);
run;
* Output results;
proc print;
var f df_num df_den p_value_A p_value_B p_value_C;
run;
Variant 1
Equality of Variances
Method Num DF Den DF F Value Pr> F
Folded F 24 29 1.04 0.9180
Variant 2
f df_num df_den p_value_A p_value_B p_value_C
1.03634 24 29 0.9180 0.4590 0.5410
- Variant 1 calculates only the p-value for hypothesis (A) as proc ttest only includes this as additional information using the test statistic
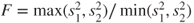 .
. - Variant 2 calculates p-values for all three hypotheses.
- In some situations SAS calculates an erroneous p-value with the variant 1. This occurs if the degree of freedom of the numerator is greater than the degree of freedom of the denominator and the test statistic
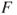 is between 1 and the median of the F-distribution. Details are given by Gallagher (2006). If this is the case, use either variant 2, or use the F-value which proc ttest provides and the formula of variant 2 for the two-sided p-value.
is between 1 and the median of the F-distribution. Details are given by Gallagher (2006). If this is the case, use either variant 2, or use the F-value which proc ttest provides and the formula of variant 2 for the two-sided p-value.
status0<-blood_pressure$mmhg[blood_pressure$status==0] status1<-blood_pressure$mmhg[blood_pressure$status==1] var.test(status0,status1,alternative="two.sided")
F = 1.0363, num df = 24, denom df = 29, p-value = 0.918
- alternative=“value” is optional and indicates the type of alternative hypothesis: “two.sides” (A); “greater” (B); “less” (C). Default is “two.sided”.
3.2.2  -test on variances of two dependent populations
-test on variances of two dependent populations
| Description: | Tests if two population variances |
| Assumptions: |
|
| Hypotheses: | (A) |
| (B) |
|
| (C) |
|
| Test statistic: |
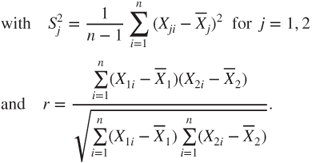
| Test decision: | Reject |
| (A) |
|
| (B) |
|
| (C) |
|
| p-value: | (A) |
| (B) |
|
| (C) |
|
| Annotations: |
|
* Calculate sample standard deviations;
* and sample size;
proc means data=iq std;
var iq1;
output out=std1 std=std1 n=n_total;
run;
proc means data=iq std;
var iq2;
output out=std2 std=std2 n=n_total;
run;
data ttest01;
merge std1 std2;
run;
* Calculate correlation coefficient;
proc corr data=iq OUTP=corr01;
var iq1 iq2;
run;
data corr02;
set corr01;
if _TYPE_='CORR' and _NAME_='IQ1';
rename IQ2 = r;
drop _TYPE_;
run;
data ttest02;
merge ttest01 corr02;
run;
* Calculate test statistic and two-sided p-value;
data ttest03;
set ttest02;
format p_value pvalue.;
df=n_total-2;
t=((df**0.5)*(std1**2-std2**2))/
(4*(1-r**2)*(std1**2)*(std2**2));
p_value=2*probt(-abs(t),df);
run;
* Output results;
proc print;
var t df p_value;
run;
t df p_value 0.007821987 18 0.9938
- There is no SAS procedure to calculate this test directly.
- The one-sided p-value for hypothesis (B) can be calculated with p_value_B=1-probt(t,df) and the p-value for hypothesis (C) with p_value_C=probt(t,df).
# Calculate sample standard deviations # and sample size std1=sd(iq$IQ1) std2=sd(iq$IQ2) n_total<-length(iq$IQ1) # Calculate correlation coefficient r<-cor(iq$IQ1,iq$IQ2) # Calculate test statistic and two-sided p-value df<-n_total-2; t<-(sqrt(df)*(std1∧2-std2∧2))/(4*(1-r∧2)*std1∧2*std2∧2) p_value=2*pt(-abs(t),df) # Output results t df p_value
> t [1] 0.007821987 > df [1] 18 > p_value [1] 0.993845
- There is no basic R function to calculate this test directly.
- The one-sided p-value for hypothesis (B) can be calculated with p_value_B=1-pt(t,df) and the p-value for hypothesis (C) with p_value_C=pt(t,df).
References
Gallagher J. 2006 The F test for comparing two normal variances: correct and incorrect calculation of the two-sided p-value. Teaching Statistics 28, 58–60.
Sheskin D.J. 2007 Handbook of Parametric and Nonparametric Statistical Procedures. Chapman & Hall.
