Chapter 16
Tests in Regression Analysis
Regression analysis investigates and models the relationship between variables. A linear relationship is assumed between a dependent or response variable 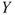 of interest and one or several independent, predictor or regressor variables. We present tests on regression parameters in simple and multiple linear regression analysis. Tests cover the hypothesis on the value of individual regression parameters as well as tests for significance of regression where the hypothesis states that none of the regressor variables has a linear effect on the response.
of interest and one or several independent, predictor or regressor variables. We present tests on regression parameters in simple and multiple linear regression analysis. Tests cover the hypothesis on the value of individual regression parameters as well as tests for significance of regression where the hypothesis states that none of the regressor variables has a linear effect on the response.
16.1 Simple linear regression
Simple linear regression relates a response variable 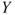 to the given outcome
to the given outcome 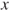 of a single regressor variable by assuming the relation
of a single regressor variable by assuming the relation 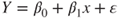 , which is linear in unknown coefficients or parameters
, which is linear in unknown coefficients or parameters 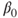 and
and  . Further
. Further  is an error term which models the deviation of the observed values from the linear relationship. In two-dimensional space this equals a straight line. For this reason simple linear regression is also called straight line regression. The value
is an error term which models the deviation of the observed values from the linear relationship. In two-dimensional space this equals a straight line. For this reason simple linear regression is also called straight line regression. The value 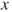 of the regressor variable is fixed or measured without error. If the regressor variable is a random variable
of the regressor variable is fixed or measured without error. If the regressor variable is a random variable 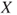 the model is commonly understood as modeling the response
the model is commonly understood as modeling the response 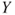 conditional on the outcome
conditional on the outcome 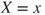 . To analyze if the regressor has an influence on the response
. To analyze if the regressor has an influence on the response  it is tested if the slope
it is tested if the slope  of the regression line differs from zero. Other tests treat the intercept
of the regression line differs from zero. Other tests treat the intercept 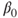 .
.
16.1.1 Test on the slope
| Description: |
Tests if the regression coefficient 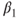 of a simple linear regression differs from a value of a simple linear regression differs from a value  . . |
| Assumptions: |
- A sample of
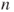 pairs pairs  is given. is given.
- The simple linear regression model for the sample is stated as
 . .
|
|
- The error term
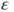 is a random variable which is Gaussian distributed with mean is a random variable which is Gaussian distributed with mean 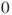 and variance and variance  , that is, , that is, 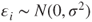 for all for all 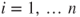 . It further holds that . It further holds that  for all for all 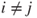 . .
|
| Hypotheses: |
(A) 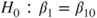 vs vs 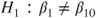 |
|
(B)  vs vs 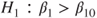 |
|
(C) 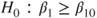 vs vs 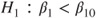 |
| Test statistic: |
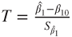 |
|
with 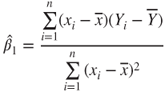 , ,  |
|
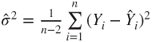 and and  |
| Test decision: |
Reject  if for the observed value if for the observed value 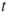 of of 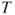 |
|
(A)  or or 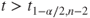 |
|
(B)  |
|
(C) 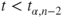 |
| p-values: |
(A) 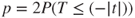 |
|
(B) 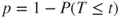 |
|
(C) 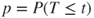 |
| Annotations: |
- The test statistic
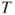 follows a t-distribution with follows a t-distribution with 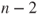 degrees of freedom. degrees of freedom.
 is the is the  -quantile of the t-distribution with -quantile of the t-distribution with 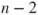 degrees of freedom. degrees of freedom.- Of special interest is the test problem
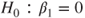 vs vs  ; the test is then also called a test for significance of regression. If ; the test is then also called a test for significance of regression. If 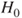 can not be rejected this indicates that there is no linear relationship between can not be rejected this indicates that there is no linear relationship between 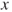 and and 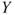 . Either . Either 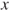 has no or little effect on has no or little effect on 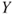 or the true relationship is not linear (Montgomery 2006, p. 23). or the true relationship is not linear (Montgomery 2006, p. 23).
- Alternatively the squared test statistic
 can be used which follows a F-distribution with can be used which follows a F-distribution with 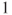 and and 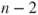 degrees of freedom. degrees of freedom.
|
Example
Of interest is the slope of the regression of weight on height in a specific population of students. For this example two hypotheses are tested with (a)
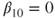
and (b)

. A dataset of measurements on a random sample of

students has been used (dataset in
Table A.6).
16.1.2 Test on the intercept
| Description: |
Tests if the regression coefficient 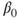 of a simple linear regression differs from a value of a simple linear regression differs from a value 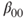 . . |
| Assumptions: |
- A sample of
 pairs pairs  is given. is given.
- The simple linear regression model for the sample is stated as
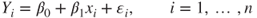 . .
- The error term
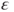 is a random variable which is Gaussian distributed with mean is a random variable which is Gaussian distributed with mean 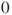 and variance and variance  , that is, , that is,  for all for all  . It further holds that . It further holds that  for all for all 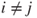 . .
|
| Hypotheses: |
(A) 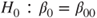 vs vs  |
|
(B) 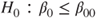 vs vs 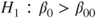 |
|
(C)  vs vs  |
| Test statistic: |
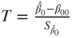 |
|
with 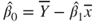 , , 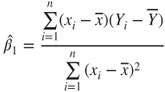 , , |
|
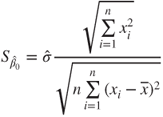 , ,  |
|
and 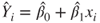 |
| Test decision: |
Reject  if for the observed value if for the observed value 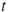 of of  |
|
(A)  or or 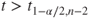 |
|
(B) 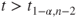 |
|
(C)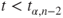 |
| p-values: |
(A) 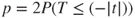 |
|
(B)  |
|
(C) 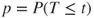 |
| Annotations: |
- The test statistic
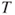 follows a t-distribution with follows a t-distribution with  degrees of freedom. degrees of freedom.
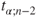 is the is the 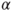 -quantile of the t-distribution with -quantile of the t-distribution with  degrees of freedom. degrees of freedom.- The hypothesis
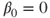 is used to test if the regression line goes through the origin. is used to test if the regression line goes through the origin.
|
Example
Of interest is the intercept of the regression of weight on height in a specific population of students. For this example two hypotheses are tested with (a)

and (b)
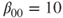
. A dataset of measurements on a random sample of
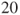
students has been used (dataset in
Table A.6).
16.2 Multiple linear regression
Multiple linear regression is an extension of the simple linear regression to more than one regressor variable. The response 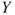 is predicted from a set of regressor variables
is predicted from a set of regressor variables 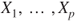 . Instead of a straight line a hyperplane is modeled. Again, the values of the regressor variables are either fixed, measured without error or conditioned on (Rencher 1998, chapter 7). Multiple linear regression is based on assuming a relation
. Instead of a straight line a hyperplane is modeled. Again, the values of the regressor variables are either fixed, measured without error or conditioned on (Rencher 1998, chapter 7). Multiple linear regression is based on assuming a relation  , which is linear in unknown coefficients or parameters
, which is linear in unknown coefficients or parameters . Further
. Further 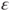 is an error term which models the deviation of the observed values from the hyperplane. To analyze if individual regressors have an influence on the response
is an error term which models the deviation of the observed values from the hyperplane. To analyze if individual regressors have an influence on the response 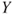 it is tested if the corresponding parameter differs from zero. Tests for significance of regression test the overall hypothesis that none of the regressor has an influence on
it is tested if the corresponding parameter differs from zero. Tests for significance of regression test the overall hypothesis that none of the regressor has an influence on 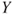 in the regression model.
in the regression model.
16.2.1 Test on an individual regression coefficient
| Description: |
Tests if a regression coefficient 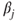 of a multiple linear regression differs from a value of a multiple linear regression differs from a value  . . |
| Assumptions: |
- A sample of
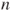 tuples tuples  is given. is given.
- The multiple linear regression model for the sample can be written in matrix notation as
 with response vector with response vector 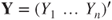 , unknown parameter vector , unknown parameter vector 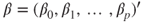 , random vector of errors , random vector of errors 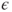 and a matrix with values of the regressors and a matrix with values of the regressors  (Montgomery et al. 2006, p. 68). (Montgomery et al. 2006, p. 68).
- The elements
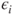 of of 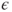 follow a Gaussian distribution with mean follow a Gaussian distribution with mean  and variance and variance 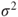 , that is, , that is,  for all for all  . It further holds that . It further holds that 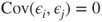 for all for all 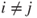 . .
|
| Hypotheses: |
(A)  vs vs  |
|
(B) 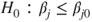 vs vs 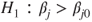 |
|
(C) 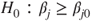 vs vs  |
| Test statistic: |
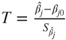 |
|
with  , ,  , , |
|
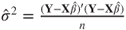 and diagjj(X′X)−1 the jjth element of the diagonal of the inverse matrix of X′X. and diagjj(X′X)−1 the jjth element of the diagonal of the inverse matrix of X′X. |
| Test decision: |
Reject 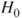 if for the observed value if for the observed value  of of 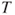 |
|
(A)  or or 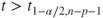 |
|
(B)  |
|
(C) 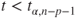 |
| p-values: |
(A)  |
|
(B) 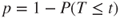 |
|
(C) 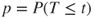 |
| Annotations: |
- The test statistic
 follows a t-distribution with follows a t-distribution with 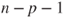 degrees of freedom. degrees of freedom.
|
|
 is the is the  -quantile of the t-distribution with -quantile of the t-distribution with 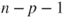 degrees of freedom. degrees of freedom.- Usually it is tested if
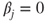 . If this hypothesis cannot be rejected it can be concluded that the regressor variable . If this hypothesis cannot be rejected it can be concluded that the regressor variable 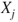 does not add significantly to the prediction of does not add significantly to the prediction of  , given the other regressor variables , given the other regressor variables 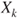 with with 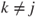 . .
- Alternatively the squared test statistic
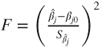 can be used which follows a F-distribution with can be used which follows a F-distribution with 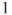 and and 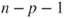 degrees of freedom. As the test is a partial test of one regressor, the test is also called a partial F-test. degrees of freedom. As the test is a partial test of one regressor, the test is also called a partial F-test.
|
Example
Of interest is the effect of sex in a regression of weight on height and sex in a specific population of students. The variable sex needs to becoded as a dummy variable for the regression model. In our example we choose the outcome male as reference, hence the new variable sex takes the value
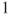
for female students and
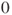
for male students. We test the hypothesis

. A dataset of measurements on a random sample of

students has been used (dataset in
Table A.6).
16.2.2 Test for significance of regression
| Description: |
Tests if there is a linear relationship between any of the regressors 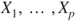 and the response and the response 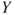 in a linear regression. in a linear regression. |
| Assumptions: |
- A sample of
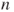 tuples tuples 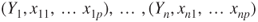 is given. is given.
- The multiple linear regression model for the sample can be written in matrix notation as
 with response vector with response vector 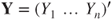 , unknown parameter vector , unknown parameter vector 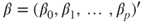 , random vector of errors , random vector of errors 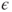 and a matrix with values of the regressors and a matrix with values of the regressors  (Montgomery et al. 2006, p.68). (Montgomery et al. 2006, p.68).
- The elements
 of of  follow a Gaussian distribution with mean follow a Gaussian distribution with mean 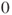 and variance and variance 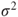 , that is, , that is,  for all for all  . It further holds that . It further holds that  for all for all  . .
|
| Hypotheses: |
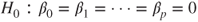 |
|
vs 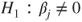 for at least one for at least one 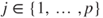 . . |
| Test statistic: |
 |
|
where the 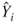 are calculated through are calculated through  |
| Test decision: |
Reject 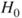 if for the observed value if for the observed value  of of  |
|
 |
| p-values: |
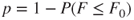 |
| Annotations: |
- The test statistic
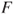 is is  -distributed. -distributed.
 is the is the 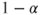 -quantile of the F-distribution with -quantile of the F-distribution with  and and  degrees of freedom. degrees of freedom.- If the null hypothesis is rejected none of the regressors adds significantly to the prediction of
 . Therefore the test is sometimes called the overall F-test. . Therefore the test is sometimes called the overall F-test.
|
Example
Of interest is the regression of weight on height and sex in a specific population of students. We test for overall significance of regression, hence the hypothesis

. A dataset of measurements on a random sample of
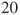
students has been used (dataset in
Table A.6).
SAS code
proc reg data=reg;
model weight=height sex;
run;
quit;
SAS output
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr> F
Model 2 1391.20481 695.60241 5.29 0.0164
Error 17 2235.79519 131.51736
Corrected Total 19 3627.00000
Remarks:
- The SAS procedure proc reg is the standard procedure for linear regression. It is a powerful procedure and we use here only a tiny part of it.
- Categorical variables can also be regressors, but care must be taken as to which value is the reference value. Here we code sex as the dummy variable, with male as the reference group.
- The quit; statement is used to terminate the procedure; proc reg is an interactive procedure and SAS then knows not to expect any further input.
R code
summary(lm(students$weight~students$height
+factor(students$sex)))
R output
F-statistic: 5.289 on 2 and 17 DF, p-value: 0.01637
Remarks:
- The function lm() performs a linear regression in R. The response variable is placed on the left-hand side of the
 symbol and the regressor variables on the right-hand side separated by a plus (+).
symbol and the regressor variables on the right-hand side separated by a plus (+).
- We use the R function factor() to tell R that sex is a categorical variable.
- The summary function gets R to return parameter estimates, p-values for the overall F-tests, p-values for tests on individual regression parameters, etc.
References
Montgomery D.C., Peck E.A. and Vining G.G. 2006 Introduction to Linear Regression Analysis, 4th edn. John Wiley & Sons, Ltd.
Rencher A.C. 1988 Multivariate Statistical Inference and Applications. John Wiley & Sons, Ltd.
![]() of interest and one or several independent, predictor or regressor variables. We present tests on regression parameters in simple and multiple linear regression analysis. Tests cover the hypothesis on the value of individual regression parameters as well as tests for significance of regression where the hypothesis states that none of the regressor variables has a linear effect on the response.
of interest and one or several independent, predictor or regressor variables. We present tests on regression parameters in simple and multiple linear regression analysis. Tests cover the hypothesis on the value of individual regression parameters as well as tests for significance of regression where the hypothesis states that none of the regressor variables has a linear effect on the response.![]() to the given outcome
to the given outcome ![]() of a single regressor variable by assuming the relation
of a single regressor variable by assuming the relation ![]() , which is linear in unknown coefficients or parameters
, which is linear in unknown coefficients or parameters ![]() and
and ![]() . Further
. Further ![]() is an error term which models the deviation of the observed values from the linear relationship. In two-dimensional space this equals a straight line. For this reason simple linear regression is also called straight line regression. The value
is an error term which models the deviation of the observed values from the linear relationship. In two-dimensional space this equals a straight line. For this reason simple linear regression is also called straight line regression. The value ![]() of the regressor variable is fixed or measured without error. If the regressor variable is a random variable
of the regressor variable is fixed or measured without error. If the regressor variable is a random variable ![]() the model is commonly understood as modeling the response
the model is commonly understood as modeling the response ![]() conditional on the outcome
conditional on the outcome ![]() . To analyze if the regressor has an influence on the response
. To analyze if the regressor has an influence on the response ![]() it is tested if the slope
it is tested if the slope ![]() of the regression line differs from zero. Other tests treat the intercept
of the regression line differs from zero. Other tests treat the intercept ![]() .
.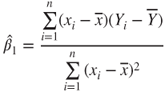 ,
, 
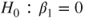 the model dependent variable=independent variable statement is sufficient.
the model dependent variable=independent variable statement is sufficient. you must add the test variable= value statement. Note, here a F-test is used, which is equivalent to the proposed t-test, because a squared t-distributed random variable with
you must add the test variable= value statement. Note, here a F-test is used, which is equivalent to the proposed t-test, because a squared t-distributed random variable with 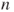 degrees of freedom is
degrees of freedom is  -distributed. The p-value stays the same. To get the t-test use the restrict variable= value statement.
-distributed. The p-value stays the same. To get the t-test use the restrict variable= value statement.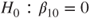 the p-value for hypothesis (B) is 1-probt(3.29,18)=0.0020 and for hypothesis (C) probt(3.29,18)=0.9980.
the p-value for hypothesis (B) is 1-probt(3.29,18)=0.0020 and for hypothesis (C) probt(3.29,18)=0.9980. symbol and the regressor variable on the right-hand side.
symbol and the regressor variable on the right-hand side. is performed by the function lm(). The hypothesis
is performed by the function lm(). The hypothesis 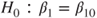 with
with  is not covered by this function but it provides the necessary statistics which we store in above example code in the object reg. In the second part of the example we extract the estimated coefficient
is not covered by this function but it provides the necessary statistics which we store in above example code in the object reg. In the second part of the example we extract the estimated coefficient 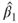 with the command reg$coeff[2,1] and its estimated standard deviations
with the command reg$coeff[2,1] and its estimated standard deviations  with the command reg$coeff[2,2]. These values are then used to perform the test.
with the command reg$coeff[2,2]. These values are then used to perform the test.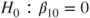 the p-value for hypothesis (B) is 1-pt(3.29,18)=0.0020 and for hypothesis (C) pt(3.29,18)=0.9980.
the p-value for hypothesis (B) is 1-pt(3.29,18)=0.0020 and for hypothesis (C) pt(3.29,18)=0.9980.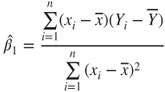 ,
,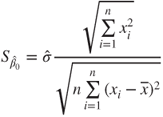 ,
,  the model dependent variable=independent variable statement is sufficient.
the model dependent variable=independent variable statement is sufficient. you must add the test intercept value statement. Note, here a F-test is used, which is equivalent to the proposed t-test, because a squared t-distributed random variable with
you must add the test intercept value statement. Note, here a F-test is used, which is equivalent to the proposed t-test, because a squared t-distributed random variable with  degrees of freedom is
degrees of freedom is 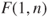 -distributed. The p-value stays the same. To get the t-test use the restrict variable= value statement.
-distributed. The p-value stays the same. To get the t-test use the restrict variable= value statement.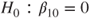 the p-value for hypothesis (B) is 1-probt(-51.82,18)=1 and for hypothesis (C) probt(-51.82,18)=0.
the p-value for hypothesis (B) is 1-probt(-51.82,18)=1 and for hypothesis (C) probt(-51.82,18)=0. symbol and the regressor variable on the right-hand side.
symbol and the regressor variable on the right-hand side.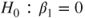 is performed by the function lm(). The hypothesis
is performed by the function lm(). The hypothesis 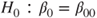 with
with 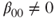 is not covered by this function but it provides the necessary statistics which we store in the example code in the object reg. In the second part of the example we extract the estimated coefficient
is not covered by this function but it provides the necessary statistics which we store in the example code in the object reg. In the second part of the example we extract the estimated coefficient  with the command reg$coeff[1,1] and its estimated standard deviation
with the command reg$coeff[1,1] and its estimated standard deviation  with the command reg$coeff[1,2]. These values are then used to perform the test.
with the command reg$coeff[1,2]. These values are then used to perform the test.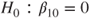 the p-value for hypothesis (B) is 1-pt(-51.82,18)=1 and for hypothesis (C) pt(-51.82,18)=0.
the p-value for hypothesis (B) is 1-pt(-51.82,18)=1 and for hypothesis (C) pt(-51.82,18)=0.![]() is predicted from a set of regressor variables
is predicted from a set of regressor variables ![]() . Instead of a straight line a hyperplane is modeled. Again, the values of the regressor variables are either fixed, measured without error or conditioned on (Rencher 1998, chapter 7). Multiple linear regression is based on assuming a relation
. Instead of a straight line a hyperplane is modeled. Again, the values of the regressor variables are either fixed, measured without error or conditioned on (Rencher 1998, chapter 7). Multiple linear regression is based on assuming a relation ![]() , which is linear in unknown coefficients or parameters
, which is linear in unknown coefficients or parameters![]() . Further
. Further ![]() is an error term which models the deviation of the observed values from the hyperplane. To analyze if individual regressors have an influence on the response
is an error term which models the deviation of the observed values from the hyperplane. To analyze if individual regressors have an influence on the response ![]() it is tested if the corresponding parameter differs from zero. Tests for significance of regression test the overall hypothesis that none of the regressor has an influence on
it is tested if the corresponding parameter differs from zero. Tests for significance of regression test the overall hypothesis that none of the regressor has an influence on ![]() in the regression model.
in the regression model. the model dependent variable=independent variables statement is sufficient. The independent variables are separated by blanks.
the model dependent variable=independent variables statement is sufficient. The independent variables are separated by blanks.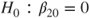 the p-value for hypothesis (B) is 1-probt(-0.48,18)= 0.6815 and for hypothesis (C) probt(-0.48,18)=0.3185.
the p-value for hypothesis (B) is 1-probt(-0.48,18)= 0.6815 and for hypothesis (C) probt(-0.48,18)=0.3185. you must add the test variable= value statement. Note, here a F-test is used, which is equivalent to the proposed t-test, because a squared t-distributed random variable with
you must add the test variable= value statement. Note, here a F-test is used, which is equivalent to the proposed t-test, because a squared t-distributed random variable with 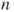 degrees of freedom is
degrees of freedom is 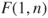 -distributed. The p-value stays the same. To get the t-test use the restrict variable= value statement.
-distributed. The p-value stays the same. To get the t-test use the restrict variable= value statement. symbol and the regressor variables on the right-hand side separated by a plus (+).
symbol and the regressor variables on the right-hand side separated by a plus (+).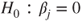 is performed by the function lm(). The hypothesis
is performed by the function lm(). The hypothesis 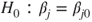 is not covered by this function but it provides the necessary statistics which can then be used. See Test 16.1.1 on how to do so.
is not covered by this function but it provides the necessary statistics which can then be used. See Test 16.1.1 on how to do so.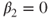 the p-value for hypothesis (B) is 1-pt(-0.477,18)=0.6805 and for hypothesis (C) pt(-0.47729,18)=0.3196.
the p-value for hypothesis (B) is 1-pt(-0.477,18)=0.6805 and for hypothesis (C) pt(-0.47729,18)=0.3196.
 symbol and the regressor variables on the right-hand side separated by a plus (+).
symbol and the regressor variables on the right-hand side separated by a plus (+).