2.2Von Neumann–Morgenstern representation

Suppose that each possible choice for our economic agent corresponds to a probability distribution on a given set of scenarios. Thus, the set X can be identified with a subset M of the set M1(S,S) of all probability distributions on a measurable space (S,S). In the context of the theory of choice, the elements of M are sometimes called lotteries. We will assume in the sequel that M is convex. The aim of this section is to characterize those preference orders on M which allow for a numerical representation U of the form

where u is a real function on S.

Definition 2.17. A numerical representation U of a preference order on M is called a von Neumann–Morgenstern representation if it is of the form (2.3).

◊

Any von Neumann–Morgenstern representation U is affine on M in the sense that

for all μ, ν ∈ M and α ∈ [0, 1]. It is easy to check that affinity of U implies the following two properties, or axioms, for a preference order on M. The first property says that a preference μ ν is preserved in any convex combination, independent of the context described by another lottery λ.

Definition 2.18. A preference relation on M satisfies the independence axiom if, for all μ, ν ∈ M, the relation μ ν implies

for all λ ∈ M and all α ∈ (0, 1].

◊

The independence axiom is also called the substitution axiom. It can be illustrated by introducing a compound lottery, which represents the distribution αμ + (1 − α)λ as a two-step procedure. First, we sample either lottery μ or λ with probability α and 1 − α, respectively. Then the lottery drawn in this first step is realized. Clearly, this is equivalent to playing directly the lottery αμ + (1 − α)λ. With probability 1 − α, the distribution λ is drawn and in this case there is no difference to the compound lottery where ν is replaced by μ. The only difference occurs when μ is drawn, and this happens with probability α. Thus, if μ ν then it seems reasonable to prefer the compound lottery with μ over the one with ν.

Definition 2.19. A preference relation on M satisfies the Archimedean axiom if for any triple μ λ ν there are α, β ∈ (0, 1) such that

◊

The Archimedean axiom derives its name from its similarity to the Archimedean principle in real analysis: For every small ε > 0 and each large x, there is some n ∈ ℕ such that n ε > x. Sometimes it is also called the continuity axiom, because it can act as a substitute for the continuity of in a suitable topology on M. More precisely, suppose that M is endowed with a topology for which convex combinations are continuous curves, i.e., αμ +(1−α)ν converges to ν or μ as α ↓ 0 or α ↑ 1, respectively. Then continuity of our preference order in this topology automatically implies the Archimedean axiom.

Remark 2.20. As an axiom for consistent behavior in the face of risk, the Archimedean axiom is less intuitive than the independence axiom. Consider the following three deterministic distributions: μ yields 1000€, λ yields 10€, and ν is the lottery where one dies for sure. Even for small α ∈ (0, 1) it is not clear that someone would prefer the gamble αν + (1 − α)μ, which involves the probability α of dying, over the conservative 10€ yielded by λ. Note, however, that most people would not hesitate to drive a car for a distance of 50 km in order to receive a premium of 1000€.

◊

Our first goal is to show that the Archimedean axiom and the independence axiom imply the existence of an affine numerical representation.

Theorem 2.21. Suppose that is a preference relation on M satisfying both the Archimedean and the independence axiom. Then there exists an affine numerical representation U of . Moreover, U is unique up to positive affine transformations, i.e., any other affine numerical representation with these properties is of the form = a U + b for some a > 0 and b ∈ ℝ.

The affinity of a numerical representation does not always imply that it is also of von Neumann-Morgenstern form; see Exercise 2.2.1 and Example 2.26 below. In two important cases, however, such an affine numerical representation will already be of von Neumann–Morgenstern form. This is the content of the following two corollaries, which we state before proving Theorem 2.21. For the first corollary, we need the notion of a simple probability distribution. This is a probability measure μ on S which can be written as a finite convex combination of Dirac masses, i.e., there exist x1, . . . , x N ∈ S and α1, . . . , αN ∈ (0, 1] withsuch that

Corollary 2.22. Suppose that M is the set of all simple probability distributions on S and that is a preference order on M that satisfies both the Archimedean and the independence axiom. Then there exists a von Neumann–Morgenstern representation U. Moreover, both U and u are unique up to positive affine transformations.

Proof. Let U be an affine numerical representation, which exists by Theorem 2.21. We define u(x) := U(δx), for x ∈ S. If μ ∈ M is of the form μ = α1δx1 + ·· · + αNδxN , then affinity of U implies

This is the desired von Neumann–Morgenstern representation.

On a finite set S, every probability measure is simple. Thus, we obtain the following result as a special case.

Corollary 2.23. Suppose that M is the set of all probability distributions on a finite set S and that is a preference order on M that satisfies both the Archimedean and the independence axiom. Then there exists a von Neumann–Morgenstern representation, and it is unique up to positive affine transformations.

For the proof of Theorem 2.21, we need the following auxiliary lemma. Its first assertion states that taking convex combination is monotone with respect to a preference order satisfying our two axioms. Its second part can be regarded as an “intermediate value theorem” for straight lines in M, and (c) is the analogue of the independence axiom for the indifference relation ∼.

Lemma 2.24. Under the assumptions of Theorem 2.21, the following assertions are true.

(a) If μ ν, then α αμ + (1 − α)ν is strictly increasing with respect to . More precisely, βμ + (1 − β)ν αμ + (1 − α)ν for 0 ≤ α < β ≤ 1.

(b) If μ ν and μ λ ν, then there exists a unique α ∈ [0, 1] with λ ∼ αμ+(1−α)ν.

(c) If μ ∼ ν, then αμ + (1 − α)λ ∼ αν + (1 − α)λ for all α ∈ [0, 1] and all λ ∈ M.

Proof. (a): Let λ := βμ + (1 − β)ν. The independence axiom implies that λ βν + (1 − β)ν = ν. Hence, for γ := α/β,

(b): Part (a) guarantees that α is unique if it exists. To show existence, we need only to consider the case μ λ ν, for otherwise we can take either α = 0 or α = 1.

The natural candidate is

If λ ∼ αμ + (1 − α)ν is not true, then one of the following two possibilities must occur:

In the first case, we apply the Archimedean axiom to obtain some β ∈ (0, 1) such that

for γ = 1−β(1−α). Since γ > α, it follows from the definition of α that γμ+(1−γ)ν λ, which contradicts (2.5). If the second case in (2.4) occurs, the Archimedean axiom yields some β ∈ (0, 1) such that

Clearly βα < α, so that the definition of α yields some γ ∈ (βα, α] with λ γμ+(1−γ)ν. Part (a) and the fact that βα < γ imply that

which contradicts (2.6).

(c): We must exclude both of the following two possibilities

To this end, we may assume that there exists some ρ ∈ M with ρ ∼ μ ∼ ν; otherwise the result is trivial. Let us assume that ρ μ ∼ ν; the case in which μ ∼ ν ρ is similar. Suppose that the first possibility in (2.7) would occur. The independence axiom yields

for all β ∈ (0, 1). Therefore,

Using our assumption that the first possibilities in (2.7) is occurring, we obtain from part (b) a unique γ ∈ (0, 1) such that, for any fixed β,

where we have used (2.8) for β replaced by βγ in the last step. This is a contradiction. The second possibility in (2.7) is excluded by an analogous argument.

Proof of Theorem 2.21. For the construction of U, we first fix two lotteries λ and ρ with λ ρ and define

the assertion is trivial if no such pair λ ρ exists. If μ ∈ M(λ, ρ), part (b) of Lemma 2.24 yields a unique α ∈ [0, 1] such that μ ∼ αλ + (1 − α)ρ, and we put U(μ) := α. To prove that U is a numerical representation of on M(λ, ρ), we must show that for ν, μ ∈ M(λ, ρ) we have U(μ) > U(ν) if and only if μ ν. To prove sufficiency, we apply part (a) of Lemma 2.24 to conclude that

Hence μ ν. Conversely, if μ ν then the preceding arguments already imply that we cannot have U(ν) > U(μ). Thus, it suffices to rule out the case U(μ) = U(ν). But if U(μ) = U(ν), then the definition of U yields μ ∼ ν, which contradicts μ ν. We conclude that U is indeed a numerical representation of restricted to M(λ, ρ).

Let us now show that M(λ, ρ) is a convex set. Take μ, ν ∈ M(λ, ρ) and α ∈ [0, 1]. Then

using the independence axiom to handle the cases λ ν and λ μ, and part (c) of Lemma 2.24 for λ ∼ ν and for λ ∼ μ. By an analogous argument it follows that αμ + (1 − α)ν ρ, which implies the convexity of the set M(λ, ρ).

Therefore, U(αμ + (1 − α)ν) is well defined; we proceed to show that it equals αU(μ) + (1 − α)U(ν). To this end, we apply part (c) of Lemma 2.24 twice:

The definition of U and the uniqueness in part (b) of Lemma 2.24 imply that

So U is indeed an affine numerical representation of on M(λ, ρ).

In a further step, we now show that the affine numerical representation U on M(λ, ρ) is unique up to positive affine transformations. So let be another affine numerical representation of on M(λ, ρ), and define

Then Û is a positive affine transformation of , and Û(ρ) = 0 = U(ρ) as well as Û(λ) = 1 = U(λ). Hence, affinity of Û and the definition of U imply

for all μ ∈ M(λ, ρ). Thus Û = U.

Finally, we have to show that U can be extended as a numerical representation to the full space M. To this end, we first take , ∈ M such that M(, ) ⊃ M(λ, ρ). By the arguments in the first part of this proof, there exists an affine numerical representation of on M(, ), and we may assume that (λ) = 1 and (ρ) = 0; otherwise we apply a positive affine transformation to . By the previous step of the proof, coincides with U on M(λ, ρ), and so is the unique consistent extension of U. Since each lottery belongs to some set M(, ), the affine numerical representation U can be uniquely extended to all of M.

Remark 2.25. In the proof of the preceding theorem, we did not use the fact that the elements of M are probability measures. All that was needed was convexity of the set M, the Archimedean, and the independence axiom. Yet, even the concept of convexity can be generalized by introducing the notion of a mixture space; see, e.g., [193], [119], or [155].

◊

Let us now return to the problem of constructing a von Neumann–Morgenstern representation for preference relations on distributions. If M is the set of all probability measures on a finite set S, any affine numerical representation is already of this form, as we saw in the proof of Corollary 2.23. However, the situation becomes more involved if we take an infinite set S. In fact, the following examples show that in this case a von Neumann–Morgenstern representation may not exist.

Exercise 2.2.1. Let M be the set of probability measures μ on S := {1, 2, . . . } for which U(μ) := limk↑∞ k2 μ(k) exists as a finite real number. Show that U is affine and induces a preference order on M which satisfies both the Archimedean and the independence axiom. Show next that U does not admit a von Neumann–Morgenstern representation.

◊

Example 2.26. Let M be set the of all Borel probability measures on S = [0, 1], and denote by λ the Lebesgue measure on S. According to the Lebesgue decomposition theorem, which is recalled in Theorem A.17, every μ ∈ M can be decomposed as

where μs is singular with respect to λ, and μa is absolutely continuous. We define a function U : M → [0, 1] by

It is easily seen that U is an affine function on M. Hence, U induces a preference order on M which satisfies both the Archimedean and the independence axioms. But cannot have a von Neumann–Morgenstern representation: Since U(δx) = 0 for all x, the only possible choice for u in (2.3) would be u ≡ 0. So the preference relation would be trivial in the sense that μ ∼ λ for all μ ∈ M, in contradiction for instance to and

◊

One way to obtain a von Neumann–Morgenstern representation is to assume additional continuity properties of , where continuity is understood in the sense of Definition 2.8. As we have already remarked, the Archimedean axiom holds automatically if taking convex combinations is continuous for the topology on M. This is indeed the case for the weak topology on the set M1(S,S) of all probability measures on a separable metric space S, endowed with the σ-field S of Borel sets. The space S will be fixed for the rest of this section, and we will simply write M1(S) = M1(S,S).

Theorem 2.27. Let M := M1(S) be the space of all probability measures on S endowed with the weak topology, and let be a continuous preference order on M satisfying the independence axiom. Then there exists a von Neumann–Morgenstern representation

for which the function u : S → ℝ is bounded and continuous. Moreover, U and u are unique up to positive affine transformations.

Proof. Let Ms denote the set of all simple probability distributions on S. Since continuity of implies the Archimedean axiom, we deduce from Corollary 2.22 that restricted to Ms has a von Neumann–Morgenstern representation.

Let us show that the function u in this representation is bounded. For instance, if u is not bounded from above, then there are x0, x1, . . . ∈ S such that u(x0) < u(x1) and u(xn) > n. Now let

Clearly, μn → δx0 weakly as n ↑ ∞. The continuity of together with the assumption that δx1 δx0 imply that δx1 μn for all large n. However, for all n, in contradiction to the fact that U(δx1) > U(μn) for sufficiently large n.

Suppose that the function u is not continuous. Then there exists some x ∈ S and a sequence (xn)n∈N ⊂ S such that xn → x but u(xn) → u(x). By taking a subsequence if necessary, we can assume that u(xn) converges to some number a ≠ u(x). Suppose that u(x)−a =: ε > 0. Then there exists some msuch that |u(xn)−a| < ε/3 for all n ≥ m. Let For all n ≥ m

Therefore δx μ δxn , although δxn converges weakly to δx, in contradiction to the continuity of . The case u(x) < a is excluded in the same manner.

Let us finally show that

defines a numerical representation of on all of M. Since u is bounded and continuous, U is continuous with respect to the weak topology on M. Moreover, Theorem A.42 states that Ms is a dense subset of the connected metrizable space M. So the proof is completed by an application of Lemma 2.16.

The scope of the preceding theorem is limited insofar as it involves only bounded functions u. This will not be flexible enough for our purposes. In the next section, for instance, we will consider risk-averse preferences which are defined in terms of concave functions u on the space S = ℝ. Such a function cannot be bounded unless it is constant. Thus, we must relax the conditions of the previous theorem. We will present two approaches. In our first approach, we fix some point x0 ∈ S and denote bythe closed metric ball of radius r around x0. The space of boundedly supported measures on S is given by

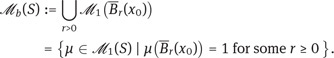
Clearly, this definition does not depend on the particular choice of x0.

Corollary 2.28. Let be a preference order on Mb(S) whose restriction to each space is continuous with respect to the weak topology. If satisfies the independence axiom, then there exists a von Neumann–Morgenstern representation

with a continuous function u : S → ℝ. Moreover, U and u are unique up to positive affine transformations.

Proof. Theorem 2.27 yields a von Neumann–Morgenstern representation of the restriction of toin terms of some continuous function The uniqueness part of the theorem implies that the restriction of ur to some smaller ball must be a equal to urup to a positive affine transformation. Thus, it is possible to find a unique continuous extension u : S → ℝ of urwhich defines a von Neumann–Morgenstern representation of on each set

Our second variant of Theorem 2.27 includes measures with unbounded support, but we need stronger continuity assumptions. Let ψ be a continuous function with values in [1,∞) on the separable metric space S. We use ψ as a gauge function and define

A suitable space of continuous test functions for measures inis provided by

These test functions can now be used to define a topology on in precisely the same way one uses the set of bounded continuous function to define the weak topology: A sequence (μn) inconverges to some if and only if

To be rigorous, one should first define a neighborhood base for the topology and then check that this topology is metrizable, so that it suffices indeed to consider the convergence of sequences; the reader will find all necessary details in Appendix A.6. We will call this topology the ψ-weak topology on If we take the trivial case ψ ≡ 1, Cψ(S) consists of all bounded continuous functions, and we recover the standard weak topology on However, by taking ψ as some unbounded function, we can also include von Neumann–Morgenstern representations in terms of unbounded functions u. The following theorem is a version of Theorem 2.27 for the ψ-weak topology. Its proof is analogous to that of Theorem 2.27, and we leave it to the reader to fill in the details.

Theorem 2.29. Let be a preference order on that is continuous in the ψ-weak topology and satisfies the independence axiom. Then there exists a numerical representation U of von Neumann–Morgenstern form

with a function u ∈ Cψ(S). Moreover, U and u are unique up to positive affine transformations.

So far, we have presented the classical theory of expected utility, starting with the independence axiom and the Archimedean axiom. However, it is well known that in reality people may not behave according to this paradigm.

Example 2.30 (Allais Paradox). The so-called Allais paradox questions the descriptive aspect of expected utility by considering the following lotteries. Lottery

yields 2500 € with a probability of 0.33, 2400 € with probability 0.66, and draws a blank with the remaining probability of 0.01. Lottery

yields 2400 € for sure. When asked, most people prefer the sure amount – even though lottery ν1 has the larger expected value, namely 2409€.

Next, consider the following two lotteries μ2 and ν2:

Here people tend to prefer the slightly riskier lottery ν2 over μ2, in accordance with the expectations of ν2 and μ2, which are 825€ and 816€, respectively.

This observation is due to M. Allais [5]. It was confirmed by D. Kahnemann and A. Tversky [171] in empirical tests where 82 %of interviewees preferred μ1 over ν1 while 83% chose ν2 rather than μ2. This means that at least 65% chose both μ1 ν1 and ν2 μ2. As pointed out by M. Allais, this simultaneous choice leads to a “paradox” in the sense that it is inconsistent with the von Neumann–Morgenstern paradigm. More precisely, any preference relation for which μ1 ν1 and ν2 μ2 are both valid violates the independence axiom, as we will show now. If the independence axiom was satisfied, then necessarily

for all α ∈ (0, 1). By taking α = 1/2 we would arrive at

which is a contradiction to the fact that

Therefore, the independence axiom was violated by at least 65% of the people who were interviewed. This effect is empirical evidence against the von Neumann–Morgenstern theory as a descriptive theory. Even from a normative point of view, there are good reasons to go beyond our present setting, and this will be done in Section 2.5. In particular, we will take a second look at the Allais paradox in Remark 2.72.

◊