For ω = (y1, . . . , yT) ∈ Ω we define ϕ(ω) by ϕ(ω) = ω if τ(ω) = T and by

otherwise, i.e., if the level k is reached before the deadline T. Intuitively, the two trajectories Zt(ω)t=0,...,T and Zt(ϕ(ω))t=0,...,T coincide up to τ(ω), but from then on the latter path is obtained by reflecting the original one on the horizontal axis at level k; see Figure 5.4.

Let Ak,l denote the set of all ω ∈ Ω such that ZT(ω) = k − l and MT ≥ k. Then ϕ is a bijection from Ak,l to the set

which coincides with {ZT = k + l}, due to our assumption l ≥ 0. Hence, the uniform distribution ℙ must assign the same probability to Ak,l and {ZT = k + l}, and we obtain our first formula. The second one follows by part one of this lemma:

Remark 5.48. Suppose that the random walk Z is defined even up to time T + 1; this can always be achieved by enlarging the probability space (Ω,F, ℙ). Then the probability in (5.32) can be rewritten as

Indeed, (5.34) is trivial in case T + k + l is not even; otherwise, we let j := (T + k + l)/2 and apply (5.31) to get

and the latter expression is equal to the right-hand side of (5.34).

◊

Formula (5.31) will change if we replace the uniform distribution ℙ by our martingale measure P∗, described in Theorem 5.39:

Let us now show how the reflection principle carries over to P∗.

Lemma 5.49 (Reflection principle for P∗). For all k ∈ ℕ and l ∈ ℕ0,

and

Proof. We show first that the density of P∗ with respect to ℙ is given by

Indeed, P∗ puts the weight

to each ω = (y1, . . . , yT) ∈ Ω which contains exactly k components with yi = +1. But for such an ω we have Z T(ω) = k − (T − k) = 2k − T, and our formula follows.

From the density formula (5.35), we get

Applying the reflection principle and using again the density formula, we see that the probability term on the right is equal to

which gives the first identity. The proof of the second one is analogous. The second set of identities now follows as in (5.33).

Remark 5.50. If we assume once again that Z is defined up to time T + 1, then the arguments from the proof of Lemma 5.49 applied to (5.34) yield the alternative representation

Example 5.51 (Up-and-in call option). Consider an up-and-in call option with payoff

where B > S0 ∨ K denotes a given barrier, and where K > 0 is the strike price. Our aim is to compute the arbitrage-free price

Clearly,

The first expectation on the right can be computed explicitly in terms of the binomial distribution. Thus, it remains to compute the second expectation, whichwe denote by I. To this end, we may assume without loss of generality that B lies within the range of possible asset prices, i.e., there exists some k ∈ ℕ such that B = S0bk. Then, by Lemma 5.49,

where

Hence, we obtain the formula

Both expectations on the right now only involve the binomial distribution with parameters p∗ and T. They can be computed as in Example 5.42, and so we get the explicit formula

where n k is the largest integer n such that T −2n ≥ k and m k is the smallest integer m such that 2m > T + k.

◊

Example 5.52 (Up-and-out call option). Consider an up-and-out call option with payoff

where K > 0 is the strike price and B > S0 ∨ K is an upper barrier for the stock price. As in the preceding example, we assume that B = S0(1 + b)k for some k ∈ ℕ. Let

denote the corresponding “plain vanilla call”, whose arbitrage-free price is given by

Since we get from Example 5.51 that

where These expectations 0022can be computed as in Example 5.51.

◊

Exercise 5.6.1. Derive a formula for the arbitrage-free price of a down-and-in put option with payoff

where K > 0 is the strike price and B < S0 is a lower barrier for the stock price. Then compute the price of the option for the following specific parameter values:

◊

In the following example, we compute the price of a lookback put option.

Example 5.53 (Lookback put option). A lookback put option corresponds to the contingent claim

see Example 5.23. In the CRR model, the discounted arbitrage-free price of is given by

The expectation of the maximum can be computed as

the formula (5.36) yields

Thus, we arrive at the expression

As before, one can give explicit formulas for the expectations occurring on the right-hand side.

◊

Exercise 5.6.2. Derive a formula for the price of a lookback call option with payoff

◊

5.7Convergence to the Black–Scholes price

In practice, a huge number of trading periods may occur between the current time t = 0 and the maturity T of a European contingent claim. Thus, the computation of option prices in terms of some martingale measure may become rather elaborate. On the other hand, one can hope that the pricing formulas in discrete time converge to a transparent limit as the number of intermediate trading periods grows larger and larger. In this section, we will formulate conditions under which such a convergence occurs.

Throughout this section, T will not denote the number of trading periods in a fixed discrete-time market model but rather a physical date. The time interval [0, T] will be divided into N equidistant time steps and the date will correspond to the kth trading period of an arbitrage-free market model. For simplicity, we will assume that each market model contains a riskless bond and just one risky asset. In the Nth approximation, the risky asset will be denoted by S(N), and the riskless bond will be defined by a constant interest rate rN > −1.

The question is whether the prices of contingent claims in the approximating market models converge as N tends to infinity. Since the terminal values of the riskless bonds should converge, we assume that

where r is a finite constant. This condition is in fact equivalent to the following one:

Let us now consider the risky assets. We assume that the initial prices do not depend on for some constant S0 > 0. The prices are random variables on some probability space where is a risk-neutral measure for each approximating market model, i.e., the discounted price process

is a with respect to the filtration Our remaining conditions will be stated in terms of the returns

First, we assume that, for each N, the random variables are independent under and satisfy

for constants αN and βN such that

Second, we assume that the variances varN under are such that

The following result can be regarded as a multiplicative version of the central limit theorem.

Theorem 5.54. Under the above assumptions, the distributions of under converge weakly to the log-normal distribution with parameters log i.e., to the distribution of

where WT has a centered normal law N (0, T) with variance T.

Proof. We may assume without loss of generality that S0 = 1. Consider the Taylor expansion

where the remainder term ρ is such that

and where δ(α, β) → 0 for α, β → 0. Applied to

this yields

where

Since is a martingale measure, we have and it follows that

In particular, ΔN → 0 in probability, and the corresponding laws converge weakly to the Dirac measure δ0. Slutsky’s theorem, as stated in Appendix A.6, asserts that it suffices to show that the distributions of

converge weakly to the normal law To this end, we will check that the conditions of the central limit theorem in the form of Theorem A.41 are satisfied.

Note that

for γN := |αN|∨ |βN|, and that

Finally,

since for p > 2

Thus, the conditions of Theorem A.41 are satisfied.

Remark 5.55. The assumption of independent returns in Theorem 5.54 can be relaxed. Instead of Theorem A.41, we can apply a central limit theorem for martingales under suitable assumptions on the behavior of the conditional variances

for details see, e.g., Section 9.3 of [57].

◊

Example 5.56. Suppose the approximating model in the Nth stage is a CRR model with interest rate

and with returns which can take the two possible values aN and bN; see Section 5.5. We assume that

for some given σ > 0. Since

we have aN < rN < bN for large enough N. Theorem 5.39 yields that the Nth model is arbitrage-free and admits a unique equivalent martingale measure The measure is characterized by

and we obtain from (5.39) that

Moreover, and we get

as N ↑ ∞. Hence, the assumptions of Theorem 5.54 are satisfied.

◊

Let us consider a derivative which is defined in terms of a function f ≥ 0 of the risky asset’s terminal value. In each approximating model, this corresponds to a contingent claim

Corollary 5.57. If f is bounded and continuous, the arbitrage-free prices of calculated under converge to a discounted expectation with respect to a log-normal distribution, which is often called the Black–Scholes price. More precisely,

where ST has the form (5.37) under P∗.

This convergence result applies in particular to the choice f (x) = (K − x)+ corresponding to a European put option with strike K. Since the put-call parity

holds for each N and in the limit N ↑ ∞, the convergence (5.40) is also true for a European call option with the unbounded payoff profile f (x) = (x − K)+.

Example 5.58 (Black–Scholes formula for the price of a call option). The limit of the arbitrage-free prices of is given by v(S0, T), where

The integrand on the right vanishes for

Let us also define

and let us denote by dy the distribution function of the standard normal distribution. Then

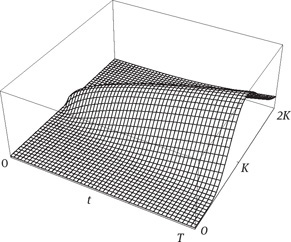
Figure 5.5: The Black–Scholes price v(x, t) of a European call option (ST − K)+ plotted as a function of the initial spot price x = S0 and the time to maturity t.

See Figure 5.5 for the plot of the function v(x, t).

◊

Remark 5.59. For fixed x and T, the Black–Scholes price of a European call option increases to the upper arbitrage bound x as σ ↑ ∞. In the limit σ ↓ 0, we obtain the lower arbitrage bound (x − e−rTK)+; see Remark 1.37.

◊

The following proposition gives a criterion for the convergence (5.40) in case f is not necessarily bounded and continuous. It applies in particular to f (x) = (x − K)+, and so we get an alternative proof for the convergence of call option prices to the Black–Scholes price.

Proposition 5.60. Let f : (0,∞) → ℝ be measurable, continuous a.e., and such that |f (x)| ≤ c (1 + x)q for some c ≥ 0 and 0 ≤ q < 2. Then

where ST has the form (5.37) under P∗.

Proof. Let us note first that by the Taylor expansion (5.38)

for a finite constant . Thus,

With this property established, the assertion follows immediately from Theorem 5.54 and the Corollaries A.49 and A.50, but we also give the following more elementary proof. To this end, we may assume that q > 0, and we define p := 2/q > 1. Then

and the assertion follows from Lemma 5.61 below.

Lemma 5.61. Suppose (μN)N∈N is a sequence of probability measures on ℝ converging weakly to μ. If f is a measurable and μ-a.e. continuous function on ℝ such that

then

Proof. We may assume without loss of generality that f ≥ 0. Then fk := f ∧ k is a bounded and μ-a.e. continuous function for each k > 0. Clearly,

Figure 5.6: The Delta Δ(x, t) of the Black–Scholes price of a European call option.

uniformly in N. Hence,

Letting k ↑ ∞, we have and convergence follows.

Let us now continue the discussion of the Black–Scholes price of a European call option where f (x) = (x − K)+. We are particularly interested how it depends on the various model parameters. The dependence on the spot price S0 = x can be analyzed via the x-derivatives of the function v(t, x) appearing in the Black–Scholes formula (5.41). The first derivative

is called the option’s Delta; see Figure 5.6. In analogy to the formula for the hedging strategy in the binomial model obtained in Proposition 5.44, Δ(x, t) determines the

Figure 5.7: The option’s Gamma Γ(x, t).

see Figure 5.7. Here stands as usual for the density of the standard normal distribution. Large Gamma values occur in regions where the Delta changes rapidly, corresponding to the need for frequent readjustments of the Delta hedging portfolio. Note that Γ is always strictly positive. It follows that v(x, t) is a strictly convex function of its first argument.

Exercise 5.7.1. Prove the formulas (5.42) and (5.43) for Delta and Gamma of a European call option.

◊

Remark 5.62. On the one hand, 0 ≤ Δ(x, t) ≤ 1 implies that

Thus, the total change of the option values is always less than a corresponding change in the asset prices. On the other hand, the strict convexity of together with (A.5) yields that for t > 0 and z > y

Figure 5.8: The Theta Θ(x, t).

Similarly, one obtains

for x < y. Thus, the relative change of option prices is larger in absolute value than the relative change of asset values. This fact can be interpreted as the leverage effect for call options; see also Example 1.43.

◊

Another important parameter is the Theta

see Figure 5.8. The fact Θ > 0 corresponds to our general observation, made in Example 5.35, that arbitrage-free prices of European call options are typically increasing functions of the maturity.

Exercise 5.7.2. Prove the formula (5.44) for the Theta of a European call option. Then show that the parameters Δ, Γ, and Θ are related by the equation

if t > 0.

◊

Equation (5.45) implies that, for (x, t) ∈ (0,∞)×(0,∞), the function v solves the partial differential equation

often called the Black–Scholes equation. Since

v(x, t) is a solution of the Cauchy problem defined via (5.46) and (5.47). This fact is not limited to call options, it remains valid for all reasonable payoff profiles f .

Proposition 5.63. Let f be a continuous function on (0,∞) such that |f (x)| ≤ c(1 + x)p for some c, p ≥ 0, and define

where St = x exp(σWt + rt − σ2t/2) and Wt has law N (0, t) under P∗. Then u solves the Cauchy problem defined by the Black–Scholes equation (5.46) and the initial condition limt↓0 u(x, t) = f (x), locally uniformly in x.

The proof of Proposition 5.63 is the content of the next exercise.

Exercise 5.7.3. In the context Proposition 5.63, use the formula (2.27) for the density of a log-normally distributed random variable to show that

where Then verify the validity of (5.46) by differentiating under the integral. Use the bound |f (x)| ≤ c(1 + x)p for some c, p ≥ 0 to justify the interchange of differentiation and integration and to verify the initial condition limt↓0 u(x, t) = f (x).

◊

Recall that the Black–Scholes price v(S0, T) was obtained as the expectation of the discounted payoff e−rT (ST − K)+ under the measure P∗. Thus, at a first glance, it may

Figure 5.9: The Rho ϱ(x, t) of a call option.

is strictly positive, i.e., the price is increasing in r; see Figure 5.9. Note, however, that the measure P∗ depends itself on the interest rate r, since E ∗[ e−rTST ] = S0. In a simple one-period model, we have already seen this effect in Example 1.43.

The parameter σ is called the volatility. As we have seen, the Black–Scholes price of a European call option is an increasing function of the volatility, and this is reflected in the strict positivity of

see Figure 5.10. The function V is often called the Vega of the call option price, and the functions Δ, Γ, Θ, ϱ, and V are usually called the Greeks (although “vega” does not correspond to a letter of the Greek alphabet).

Exercise 5.7.4. Prove the respective formulas (5.48) and (5.49) for Rho and Vega of a European call option. Then derive formulas for the option’s Vanna,

and the option’s Volga, which is also called Vomma,

◊

Figure 5.10: The Vega V (x, t).

The prices of the risky asset in each discrete-time model are considered as a continuous process defined as at the dates and by linear interpolation in between. Theorem 5.54 shows that the distributions ofconverge for each fixed t weakly to the distribution of

where Wt has a centered normal distribution with variance t. In fact, one can prove convergence in the much stronger sense of a functional central limit theorem: The laws of the processes considered as C[0, T]-valued random variables on converge weakly to the law of a geometric Brownian motion S = (St)0≤t≤T, where each St is of the form (5.50), and where the process W = (Wt)0≤t≤T is a standard Brownian motion or Wiener process. A Wiener process is characterized by the following properties:

–W0 = 0 almost surely,

–is continuous,

–for each sequence 0 = t0 < t1 < ·· · < tn = T, the increments

are independent and have normal distributions N (0, ti − ti−1);

see, e.g., [177]. This multiplicative version of a functional central limit theorem follows as above if we replace the classical central limit theorem by Donsker’s invariance principle; for details see, e.g., [101]. Sample paths of Brownian motion and geometric Brownian motion can be found in Figures 5.11 and 5.12.

Figure 5.11: A sample path of Brownian motion.

is a martingale under ℙ, since

for 0 ≤ s ≤ t ≤ T. In fact, ℙ is the only probability measure equivalent to ℙ with that property.

As in discrete time, uniqueness of the equivalent martingale measure implies completeness of the model. Let us sketch the construction of the replicating strategy for a given European option with reasonable payoff profile f (ST), for example a call

Figure 5.12: A sample path of geometric Brownian motion.