Definition 5.1. A family (Ft)t=0,...,T of σ-algebras satisfying (5.1) is called a filtration. In this case, (Ω,F, (Ft)t=0,...,T , P) is also called a filtered probability space.

◊

To simplify the presentation, we will assume from now on that

Let (E, E ) be a measurable space. A stochastic process with state space (E, E ) is given by a family of E-valued random variables on (Ω,F, P) indexed by time. In our context, the typical parameter sets will be {0, . . . , T} or {1, . . . , T}, and the state space will be some Euclidean space.

Definition 5.2. A stochastic process Y = (Yt)t=0,...,T is called adapted with respect to the filtration (Ft)t=0,...,T if each Yt is Ft-measurable. A stochastic process Z = (Zt)t=1,...,T is called predictable with respect to (Ft)t=0,...,T if each Zt is Ft−1-measurable.

◊

Note that in our definition predictable processes start at t = 1 while adapted processes are also defined at t = 0. In particular, the asset prices S = (St)t=0,...,T form an adapted stochastic process with values in ℝd+1.

Definition 5.3. A trading strategy is a predictable ℝd+1-valued process

The value of a trading strategy corresponds to the quantity of shares of the ith asset held during the tth trading period between t −1 and t. Thus, is the amount invested into the ith asset at time t − 1, while is the resulting value at time t. The total value of the portfolio t at time t − 1 is

By time t, the value of the portfolio t has changed to

The predictability of expresses the fact that investments must be allocated at the beginning of each trading period, without anticipating future price increments.

Definition 5.4. A trading strategy is called self-financing if

Intuitively, (5.3) means that the portfolio is always rearranged in such a way that its present value is preserved. It follows that the accumulated gains and losses resulting from the asset price fluctuations are the only source of variations of the portfolio value:

In fact, is self-financing if and only if (5.4) holds for t = 1, . . . , T−1. It follows through summation over (5.4) that

Here, the constant 1 · S0 can be interpreted as the initial investment for the purchase of the portfolio 1.

Example 5.5. Often it is assumed that the 0th asset plays the role of a locally riskless bond. In this case, one takes and one lets evolve according to a spot rate rt ≥ 0: At time t, an investment x made at time t − 1 yields the payoff x(1 + rt). Thus, a unit investment at time 0 produces the value

at time t. An investment in S0 is “locally riskless” if the spot rate rt is known beforehand at time t − 1. This idea can be made precise by assuming that the process r is predictable.

◊

Without assuming predictability as in the preceding example, we assume from now on that

This assumption allows us to use the 0th asset as a numéraire and to form the discounted price processes

Then and expresses the value of the remaining assets in units of the numéraire. As explained in Remark 1.11, discounting allows comparison of asset prices which are quoted at different times.

Definition 5.6. The (discounted) value process V = (Vt)t=0,...,T associated with a trading strategy is given by

The gains process associated with is defined as

◊

Clearly,

so Vt can be interpreted as the portfolio value at the end of the tth trading period expressed in units of the numéraire asset. The gains process

reflects, in terms of the numéraire, the net gains which have accumulated through the trading strategy up to time t. For a self-financing trading strategy , the identity

remains true if all relevant quantities are computed in units of the numéraire. This is the content of the following simple proposition.

Proposition 5.7. For a trading strategy the following conditions are equivalent:

Proof. By dividing both sides of (5.3) by Sit is seen that condition (b) is a reformulation of Definition 5.4. Moreover, (b) holds if and only if

for t = 1, . . . , T − 1, and this identity is equivalent to (c).

Remark 5.8. The numéraire component of a self-financing trading strategy satisfies

Since

the entire process ξ0 is determined by the initial investment V0 and the d-dimensional process ξ. Consequently, if a constant V0 and an arbitrary d-dimensional predictable process ξ are given, then we can use (5.7) and (5.6) as the definition of a predictable process ξ0, and this construction yields a self-financing trading strategy := (ξ0, ξ). In dealing with self-financing strategies , it is thus sufficient to focus on the initial investment V0 and the d-dimensional processes X and ξ.

◊

Remark 5.9. Different economic agents investing into the same market may choose different numéraires. For example, consider the following simple market model in which prices are quoted in euros (€) as the domestic currency. Let S0 be a locally riskless €-bond with the predictable spot rate process r0, i.e.,

and let S1 describe the price of a locally riskless investment into US dollars ($). Since the price of this $-bond is quoted in €, the asset S1 is modeled as

where r1 is the spot rate for a $-investment, and Ut denotes the price of 1$ in terms of €, i.e., Ut is the exchange rate of the $ versus the €. While it may be natural for European investors to take S0 as their numéraire, it may be reasonable for an American investor to choose S1. This simple example explains why it may be relevant to check which concepts and results of our theory are invariant under a change of numéraire; see, e.g., the discussion at the end of Section 5.2.

◊

Exercise 5.1.1. Consider a market model with two assets which are modeled as usual by the stochastic process S = (S0, S1) that is adapted to the filtration (Ft)t=0,...,T. Decide which of the following processes ξ are predictable and which in general are not.

◊

5.2Arbitrage opportunities and martingale measures

Intuitively, an arbitrage opportunity is an investment strategy that yields a positive profit with positive probability but without any downside risk.

Definition 5.10. A self-financing trading strategy is called an arbitrage opportunity if its value process V satisfies

◊

The existence of such an arbitrage opportunity may be regarded as a market inefficiency in the sense that certain assets are not priced in a reasonable way. In this section, we will characterize those market models which do not allow for arbitrage opportunities. Such models will be called arbitrage-free. The following proposition shows that the market model is arbitrage-free if and only if there are no arbitrage opportunities for each single trading period. Later on, this fact will allow us to apply the results of Section 1.6 to our multi-period model.

Proposition 5.11. The market model admits an arbitrage opportunity if and only if there exist t ∈ {1, . . . , T} and η ∈ L0(Ω,Ft−1, P;ℝd) such that

Proof. To prove necessity, take an arbitrage opportunity = (ξ0, ξ) with value process V, and let

Then t ≤ T by assumption, and either Vt−1 = 0 P-a.s. or P[ Vt−1 < 0 ] > 0. In the first case, it follows that

Thus, η := ξt satisfies (5.8). In the second case, we let η := ξt {Vt−1<0}. Then η is Ft−1-measurable, and

The expression on the right-hand side is nonnegative and strictly positive with a positive probability, so (5.8) holds.

Now we prove sufficiency. For t and η as in (5.8), define a d-dimensional predictable process ξ by

Via (5.7) and (5.6), ξ uniquely defines a self-financing trading strategy = (ξ0, ξ) with initial investment V0 = 0. Since the corresponding value process satisfies VT = η · (Xt − Xt−1), the strategy is an arbitrage opportunity.

Exercise 5.2.1. Let V be the value process of a self-financing strategy in an arbitrage-free market model. Prove that the following two implications hold for all t ∈ {0, . . . , T − 1} and A ∈ Ft with P[ A ] > 0.

◊

Definition 5.12. A stochastic process M = (Mt)t=0,...,T on a filtered probability space (Ω,F, (Ft), Q) is called a martingale if M is adapted, satisfies EQ[ |Mt| ] < ∞for all t, and if

A martingale can be regarded as the mathematical formalization of a “fair game”: For each time s and for each horizon t > s, the conditional expectation of the future gain M t − Ms is zero, given the information available at s.

Exercise 5.2.2. Let M = (Mt)t=0,...,T be an adapted process on (Ω,F, (Ft), Q) such that EQ[ |Mt| ] < ∞for all t. Show that the following conditions are equivalent.

(a) M is a martingale.

(b) Mt = EQ[Mt+1 | Ft ] for 0 ≤ t ≤ T − 1.

(c) There exists F ∈ L1(Ω,FT , Q) such that Mt = EQ[ F | Ft ] for t = 0, . . . , T, that is, M arises as a sequence of successive conditional expectations.

◊

Exercise 5.2.3. Let be a probability measure on (Ω,F, (Ft)0≤t≤T) that is absolutely continuous with respect to Q. Show that the density process

is a martingale with respect to Q.

◊

Whether or not a given process M is a martingale depends on the underlying probability measure Q. If we wish to emphasize the dependence of the martingale property of M on a particular measure Q, we will say that M is a Q-martingale or that M is a martingale under the measure Q.

Definition 5.13. A probability measure Q on (Ω,FT) is called a martingale measure if the discounted price process X is a (d-dimensional) Q-martingale, i.e.,

A martingale measure P∗ is called an equivalent martingale measure if it is equivalent to the original measure P on FT. The set of all equivalent martingale measures is denoted by P.

◊

The following result is a version of Doob’s fundamental “systems theorem” for martingales. It states that a fair game admits no realistic gambling system which produces a positive expected gain. Recall that Y− denotes the negative part −(Y ∧ 0) of a random variable Y.

Theorem 5.14. For a probability measure Q, the following conditions are equivalent.

(a) Q is a martingale measure.

(b) If = (ξ0, ξ) is self-financing and ξ is bounded, then the value process V of is a Q-martingale.

(c) If = (ξ0, ξ) is self-financing and its value process V satisfies < ∞, then V is a Q-martingale.

(d) If = (ξ0, ξ) is self-financing and its value process V satisfies VT ≥ 0 Q-a.s., then EQ[ VT ] = V0.

Proof. (a)⇒(b): Let V be the value process of a self-financing trading strategy = (ξ0, ξ) such that there is a constant c such that |ξ i| ≤ c for all i. Then

Since each |Xk| belongs to L1(Q), we have EQ[ |Vt| ] < ∞. Moreover, for 0 ≤ t ≤ T − 1,

where we have used that ξt+1 is Ft-measurable and bounded. (b)⇒(c): We will show the following implication:

Since < ∞by assumption, we will then get

due to Jensen’s inequality for conditional expectations. Repeating this argument will yield < ∞ and EQ[ Vt | Ft−1 ] = Vt−1 for all t. Since V0 is a finite constant, we will also get EQ[ Vt ] = V0, which together with the fact that < ∞ implies Vt ∈ L1(Q) for all t. Thus, the martingale property of V will follow.

To prove (5.10), note first that EQ[ Vt | Ft−1 ] is well defined due to our assumption < ∞. Next, let for a > 0. Then is a martingale increment by condition (b). In particular, · (Xt − X t−1) ∈ L1(Q) and EQ[ · (Xt − Xt−1) | Ft−1 ] = 0. Hence,

By sending a ↑ ∞, we obtain (5.10).

(c)⇒(d): By (5.2), every Q-martingale M satisfies

(d)⇒(a): To prove that ∈ L1(Q) for given i and t, consider the deterministic process ξ defined by := {s≤t} and := 0 for j ≠ i. By Remark 5.8, ξ can be complemented with a predictable process ξ0 such that = (ξ0, ξ) is a self-financing strategy with initial investment The corresponding value process satisfies

From (d) we get

which yields

Condition (a) will follow if we can show that for given t, i, and A ∈ Ft−1. To this end, we define a d-dimensional predictable process η by and As above, we take a predictable process η0 such that η = (η0, η) is a self-financing strategy with initial investmentIts terminal value is given by

Using (d) yields

By iicomparing this identity with (5.11), we conclude that

Remark 5.15. (a) Suppose that the “objective” measure P is itself a martingale measure, so that the fluctuation of prices may be viewed as a fair game. In this case, the preceding theorem shows that there are no realistic self-financing strategies which would generate a positive expected gain. Thus, the assumption P ∈ P is a strong version of the so-called efficient market hypothesis. For a market model containing a locally risk-less bond, this strong hypothesis would imply that risk-averse investors would not be attracted towards investing into the risky assets if their expectations are consistent with P; see Example 2.40.

(b) The strong assumption P ∈ P implies, in particular, that there is no arbitrage opportunity, i.e., no self-financing strategy with positive expected gain and without any downside risk. Indeed, Theorem 5.14 implies that the value process of any self-financing strategy with V0 ≤ 0 and VT ≥ 0 satisfies E[ VT ] = V0, hence VT = 0P-almost surely. The assumption that the market model is arbitrage-free may be viewed as a much milder and hence more flexible form of the efficient market hypothesis.

◊

We can now state the following dynamic version of the “fundamental theorem of asset pricing”, which relates the absence of arbitrage opportunities to the existence of equivalent martingale measures.

Theorem 5.16. The market model is arbitrage-free if and only if the set P of all equivalent martingale measures is nonempty. In this case, there exists a P∗ ∈ P with bounded density dP∗/dP.

Proof. Suppose first that there exists an equivalent martingale measure P∗. Then it follows as in Remark 5.15 (b) that the market model in which the probability measure P is replaced by P∗ is arbitrage-free. Since the notion of an arbitrage opportunity depends on the underlying measure only through its null sets and since these are common for the two equivalent measures P and P∗, it follows that also the original market model is arbitrage-free.

Let us turn to the proof of the converse assertion. For t ∈ {1, . . . , T}, we define

By Proposition 5.11, the market model is arbitrage-free if and only if

holds for all t. Note that (5.13) depends on the measure P only through its null sets.

Condition (5.13) allows us to apply Theorem 1.55 to the tth trading period. For t = T we obtain a probability measure T ≈ P which has a bounded density dT /dP and which satisfies

Now suppose that we already have a probability measure t+1 ≈ P with a bounded density dt+1/dP such that

The equivalence of t+1 and P implies that (5.13) also holds with P replaced by t+1. Applying Theorem 1.55 to the tth trading period yields a probability measure t with a bounded Ft-measurable density Z t := dt/dt+1 > 0 such that

Clearly, t is equivalent to P and has a bounded density, since

is the product of two bounded densities. Moreover, if t + 1 ≤ k ≤ T, Proposition A.16 and the Ft-measurability of Z t = dt/dt+1 imply

Hence, (5.14) carries over from t+1 to t. We can repeat this recursion until finally P∗ := 1 yields the desired equivalent martingale measure.

Clearly, the absence of arbitrage in the market is independent of the choice of the numéraire, while the set P of equivalent martingale measures generally does depend on the numéraire. In order to investigate the structure of this dependence, suppose that the first asset S1 is P-a.s. strictly positive, so that it can serve as an alternative numéraire. The price process discounted by S1 is denoted by

Let be the set of equivalent martingale measures for Y. Then ≠ ∅ if and only if P ≠ ∅, according to Theorem 5.16 and the fact that the existence of arbitrage opportunities is independent of the choice of the numéraire.

Proposition 5.17. The two sets P and are related via the identity

Proof. The process is a P∗-martingale for any P∗ ∈ P. In particular, and the formula

defines a probability measure ∗ which is equivalent to P. Moreover, by Proposition A.16,

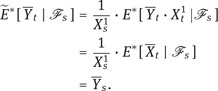
Hence, ∗ is an equivalent martingale measure for Y, and it follows that

Reversing the roles of X and Y yields the identity of the two sets.

Remark 5.18. Unless is P-a.s. constant, the two sets P and satisfy

This can be proved as in Remark 1.12.

◊

Exercise 5.2.4. Let be the P-a.s. strictly positive discounted price process of a risky asset. The corresponding returns are

so that

We take as filtration Ft = σ(X0, . . . , Xt).

(a) Show that X is a P-martingale if the (t) are independent and integrable random variables with E[t ] = 0.

(b) Now give necessary and sufficient conditions on the (t) such that X is a P-martingale.

(c) Construct an example in which X is a martingale but the returns (t) are not independent.

◊

Exercise 5.2.5. Let Z1, . . . , ZT be independent standard normal random variables on (Ω,F, P), and let Ft be the σ-field generated by Z1, . . . , Zt, where t = 1, . . . , T. We also let F0 := {∅, Ω}. For constants and mi ∈ ℝ we now define the discounted price process of a risky asset as the following sequence of log-normally distributed random variables,

Construct an equivalent martingale measure for X1 under which the random variables X have still a log-normal distribution.

◊

Exercise 5.2.6. For a square-integrable random variable X on (Ω,F, P) and a σ-algebra F0 ⊂ F, the conditional variance of X given F0 is defined as

Show that

and that

◊

Exercise 5.2.7. Let Y1 and Y2 be jointly normal random variables with mean 0, variance 1, and correlation ϱ ∈ (−1, 1). That is, the joint distribution of (Y1, Y2) has the density

(a) Compute the conditional expectation E[ Y2 | Y1 ].

(b) Compute the conditional variance var(Y2| Y1).

(c) For constants m, σ ∈ ℝ compute E[ eσY2+m | Y1 ].

◊

Exercise 5.2.8. Let Y1 and Y2 be as in Exercise 5.2.7. We use the Yi to construct a log-normal price process in analogy to (5.15):

for constants and mi ∈ ℝ (i = 1, 2).

(a) Compute the conditional expectation

(b) Construct an equivalent martingale measure for the price process in (5.16) if the filtration is the one generated by the process X1.

◊

Exercise 5.2.9. Let X0, X1, . . . describe the discounted prices of a risky asset in a market model with infinite time horizon that is modeled on a filtered probability space (Ω, (Ft)t=0,1,... , P). Suppose that every market model X0, . . . , X T with finite time horizon T ∈ ℕ is arbitrage-free.

(a) Show that there exists a sequence of probability measures such that is defined on (Ω,FT), is equivalent to P on FT, and such that the restriction of to FT−1 equals for all A ∈ FT−1.

(b) Can you give conditions under which arises as the restriction to FT of a measure P∗ that is defined on

Hint: You may choose a setting in which one can apply the Kolmogorov extension theorem.

◊