2.6Probability measures with given marginals

In this section, we study the construction of probability measures with given marginals. In particular, this will yield the missing implication in the characterization of uniform preference in Theorem 2.57, but the results in this section are of independent interest. We focus on the following basic question: Suppose μ1 and μ2 are two probability measures on S, and Λ is a convex set of probability measures on S × S; when does Λ contain some μ which has μ1 and μ2 as marginals?

The answer to this question will be given in a general topological setting. Let S be a Polish space, and let us fix a continuous function ψ on S with values in [1, ∞). As in Section 2.2 and in Appendix A.6, we use ψ as a gauge function in order to define the space of measures

and the space of continuous test functions

The ψ-weak topology on Mψ 1 (S) is the coarsest topology such that

is a continuous mapping for all f ∈ C ψ(S); see Appendix A.6 for details. On the product space S × S, we take the gauge function

and define the corresponding setwhich will be endowed with the ψ-weak topology.

Theorem 2.89. Suppose that is convex and closed in the ψ-weak topology, and that μ1, μ2 are probability measures in Then there exists some μ ∈ Λ with marginal distributions μ1 and μ2 if and only if

Theorem 2.89 is due to V. Strassen [266]. Its proof boils down to an application of the Hahn–Banach theorem; the difficult part consists in specifying the right topological setting. First, let us investigate the relations betweenandTo this end, we define mappings

that yield the ith marginal distribution of a measure

for all f ∈ Cψ(S).

Lemma 2.90. π1 and π2 are continuous and affine mappings from to

Proof. Suppose that λn converges to λ inlet Clearly, and thus

Therefore, π1 is continuous, and the same is true of π2. Affinity is obvious.

Now, let us consider the linear space

spanned by For ρ = αμ − βν ∈ E the integral against a function f ∈ Cψ(S) is well-defined and given by

In particular, is linear functional on E, so we can regard Cψ(S) as a subset of the algebraic dual E∗ of E. Note that for all f ∈ Cψ(S) implies ρ = , i.e., Cψ(S) separates the points of E. We endow E with the coarsest topology σ(E, Cψ(S)) for which all maps

are continuous; see Definition A.61. With this topology, E becomes a locally convex topological vector space.

Lemma 2.91. Under the above assumptions,is a closed convex subset of E, and the relative topology of the embedding coincides with the ψ-weak topology.

Proof. The sets of the form

with ρ ∈ E, n ∈ ℕ, fi ∈ Cψ(S), and ε > 0 form a base of the topology σ(E, Cψ(S)). Thus, if U ⊂ E is open, then every point μ ∈ U ∩ possesses some neighborhood Uε(μ; f1, . . . , fn) ⊂ U. But Uε(μ; f1, . . . , fn) ∩ is an open neighborhood of μ in the ψ-weak topology. Hence, (S) is open in the ψ-weak topology. Similarly, one shows that every open set (S) is of the form (S) for some open subset U of E. This shows that the relative topology coincides with the ψ-weak topology.

Moreover,(S) is an intersection of closed subsets of E:

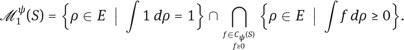
Therefore,(S) is closed in E.

Next, let E2 denote the product space E × E. We endow E2 with the product topology for which the sets U × V with U, V ∈ σ(E, Cψ(S)) form a neighborhood base. Clearly, E2 is a locally convex topological vector space.

Lemma 2.92. Every continuous linear functional on E2 is of the form

for some f1, f2 ∈ Cψ(S).

Proof. By linearity, is of the form (ρ1, ρ2) = 1(ρ1)+2(ρ2), where 1(ρ1) := (ρ1, 0) and 2(ρ2) := (0, ρ2). By continuity of , the set

is open in E2 and contains the point (0, 0). Hence, there are two open neighborhoods U1, U2 ⊂ E such that (0, 0) ∈ U1 × U2 ⊂ V. Therefore,

i.e., 0 is an interior point of It follows that the i are continuous at 0, which in view of their linearity implies continuity everywhere on E. Finally, we may conclude from Proposition A.62 that each i is of the form for some fi ∈ Cψ(S).

The proof of the following lemma uses the characterization of compact sets for the ψ-weak topology that is stated in Corollary A.50. It is here that we need our assumption that S is Polish.

Lemma 2.93. If Λ is a closed convex subset ofthen

is a closed convex subset of E2.

Proof. Convexity follows from the affinity of the projections πi, as established in Lemma 2.90. To prove closedness, it is enough to show that H Λ is closed inbecause Lemma 2.91 implies that the relative topology induced by E2 on coincides with the product topology for the ψ-weak topology. This is a metric topology by Corollary A.48. So let (μn , νn) ∈ H Λ, n ∈ ℕ, be a sequence converging to some in the product topology. Since both sequences (μn)n∈N and (νn)n∈N are relatively compact for the ψ-weak topology, Corollary A.50 yields functions ϕi : S → [1,∞], i = 1, 2, such that sets of the form kk ∈ ℕ, are relatively compact in S and such that

For each n, there exists λn ∈ Λ such that π1λn = μn and π2λn = νn. Hence, if we let then

Moreover, we claim that each set {ϕ ≤ kψ} is relatively compact in S × S. To prove this claim, let li ∈ ℕ be such that

Then, since ψ ≥ 1,

and the right-hand side is a relatively compact set in S × S. It follows from Corollary A.50 that the sequence (λn)n∈N is relatively compact for the ψ-weak topology. Any accumulation point λ of this sequence belongs to the closed set Λ. Moreover, λ has marginal distributions μ and ν, since the projections πi are continuous according to Lemma 2.90. Hence (μ, ν) ∈ HΛ.

Proof of Theorem 2.89. Let μ1, μ2 ∈ be given. Since HΛ is closed and convex in E2 by Lemma 2.93, we may apply Theorem A.60 with B := {(μ1, μ2)} and C := HΛ: We conclude that (μ1, μ2) /∈ HΛ if and only if there exists a linear functional on E2 such that

Applying Lemma 2.92 to completes the assertion.

We will now use Theorem 2.89 to deduce the remaining implication of Theorem 2.57. We consider here a more general, d-dimensional setting. To this end, let x = (x1, . . . , xd) and y = (y1, . . . , yd) be two d-dimensional vectors. We will say that x ≤ y if xi ≤ yi for all i. A function on ℝd is called increasing, if it is increasing with respect to the partial order ≤.

Theorem ∫ 2.94. Suppose μ1 and μ2 are Borel probability measures on ℝd with ∫|x|μi(dx) < ∞ for i = 1,2. Then the following assertions are equivalent.

(a) dμ2 for all increasing concave functions f on ℝd.

(b) There exists a probability space (Ω,F, P) with random variables X1 and X2 having distributions μ1 and μ2, respectively, such that

(c) There exists a kernel Q(x, dy) on ℝd such that

and such that μ2 = μ1Q.

Proof. (a)⇒(b): We will apply Theorem 2.89 with S := ℝd and with the gauge functions ψ(x) := 1 + |x| and ψ(x, y) := ψ(x) + ψ(y). We denote by Cb(ℝd) the set of bounded and continuous functions on ℝd. Let

Each single set of the intersection is convex and closed in because the functions g(x, y) := yf (x) and (x, y) := xf (x) belong to Cψ(ℝd × ℝd) for f ∈ C b(S). Therefore, Λ itself is convex and closed.

Suppose we can show that Λ contains an element P that has μ1 and μ2 as marginal distributions. Then we can take Ω := ℝd × ℝd with its Borel σ-algebra F, and let X1 and X2 denote the canonical projections on the first and the second components, respectively. By definition, X i will have the distribution μi, and

By monotone class arguments (see, e.g., Theorem I.1.8 in [226]), we may thus conclude that

so that the assertion will follow.

It remains to prove the existence of P. To this end, we will apply Theorem 2.89 with the set Λ defined above. Take a pair f1, f2 ∈ Cψ(ℝd), and let

Then 2 is concave, increasing, and dominates f2. In fact, 2 is the smallest function with these properties. From (a), we have

We will establish the condition in Theorem 2.89 for our set Λ by showing that for r < r0 we have

To this end, let for z ∈ ℝd

and

Then g2 is increasing and g2(z) ≥ f2(z), because δz ∈ Λz. Moreover, if ν1 ∈ Λz1 and ν2 ∈ Λz2 , then

for α ∈ [0, 1]. Therefore, g2 is concave, and we conclude that g2 ≥2 (recall that 2 is the smallest increasing and concave function dominating f2). Hence, r < f1(z) + g2(z) for some z ∈ ℝd, i.e., there exists some ν ∈ Λz such that the product measure λ := δz ⊗ ν satisfies

But λ = δz ⊗ ν ∈ Λ.

(b)⇒(c): This follows as in the proof of the implication (f)⇒(g) of Theorem 2.57 by using regular conditional distributions.

(c)⇒(a): As in the proof of (g)⇒(a) of Theorem 2.57, this follows by an application of Jensen’s inequality.

By the same arguments as for Corollary 2.61, we obtain the following result from Theorem 2.94.

Corollary ∫ 2.95. Suppose μ1 and μ2 are Borel probability measures on ℝd such that ∫|x|μi(dx) < ∞, for i = 1,2. Then the following conditions are equivalent.

(a) for all concave functions f on ℝd.

(b) There exists a probability space (Ω,F, P) with random variables X1 and X2 having distributions μ1 and μ2, respectively, such that

(c) There exists a kernel Q(x, dy) on ℝd such that

(i.e., Q is a mean-preserving spread) and such that μ2 = μ1Q.

We conclude this section with a generalization of Theorem 2.68. Let S be a Polish space which is endowed with a preference order . We will assume that is continuous in the sense of Definition 2.8. A function on S will be called increasing if it is increasing with respect to .

Theorem 2.96. For two Borel probability measures μ1 and μ2 on S, the following conditions are equivalent.

(a) for all bounded, increasing, and measurable functions f on S.

(b) There exists a probability space (Ω,F, P) with random variables X1 and X2 having distributions μ1 and μ2, respectively, such that X1 X2 P-a.s.

(c) There exists a kernel Q on S such that μ2 = μ1Q and

Proof. (a)⇒(b): We will apply Theorem 2.89 with the gauge function ψ ≡ 1, so that is just the space M1(S) of all Borel probability measures on S with the usual weak topology. Then ψ ≡ 2 which is equivalent to taking ψ := 1. Let

This set M is closed in S × S. Hence, the portmanteau theorem in the form of Theorem A.43 implies that the convex set

is closed in M1(S × S). For f2 ∈ Cb(S), let

Then 2 is bounded, increasing, and dominates f2. Therefore, if f1 ∈ Cb(S),

If x y, then the product measure λ := δx ⊗ δy is contained in Λ, and so

Hence, all assumptions of Theorem 2.89 are satisfied, and we conclude that there exists a probability measure P ∈ Λ with marginals μ1 and μ2. Taking Ω := S × S and Xi as the projection on the ith coordinate finishes the proof of (a)⇒(b).

(b)⇒(c) follows as in the proof of Theorem 2.57 by using regular conditional distributions.

(c)⇒(a) is proved as the corresponding implication of Theorem 2.68.