Chapter Three

Recognition

3.0 INTRODUCTION

When TN matrices are first encountered, it may seem that examples should be rate and that checking for TN or TP is tedious and time consuming.

However, TN matrices enjoy tremendous structure, as a result of requiring all minors to be nonnegative. This intricate structure actually makes it easier to determine when a matrix is TP than to check when it is a P-matrix, which formally involves far fewer minors.

Furthermore, this structure is one of the reasons that TN matrices arise in many applications in both pure and applied mathematics. We touch on one such application here, which also highlights the structure of TN matrices.

Vandermonde matrices arise in the problem of determining a polynomial of degree at most n-1 that interpolates n data points. Suppose that n data points are given. The goal is to construct a polynomial that satisfies

(3.1)

The n equations in (3.1) are expressed by the linear system

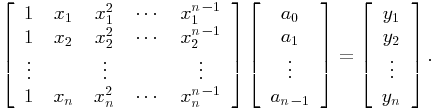(3.2)

The n-by-n coefficient matrix in (3.2) is called a Vandermonde matrix, and we denote it by (see also Chapter 0). The determinant of the n-by-n Vandermonde matrix in (3.2) is given by the formula ; see [HJ85, p. 29]. Thus, if , then has positive entries, positive leading principal minors, and, in particular, a positive determinant.

Consider a 3-by-3 Vandermonde matrix V with , , and :

(3.3)

The inequalities are actually sufficient to guarantee that all minors of V in (3.3) are positive. Indeed, any 2-by-2 submatrix of V has the form

with , i<j, , and . Since , it follows that det A > 0. Hence, in this case, V is TP.

More generally, it is known [GK02, p. 111] that if , then is TP. Here is an outline of a proof similar to that given in [GK02]: Consider a k-by-k submatrix of , which is of the form , where , , , and . Let be a real polynomial. Descartes’s rule of signs ensures that the number of positive real roots of f(x) does not exceed the number of sign changes among the coefficients ; so, f(x) has at most k-1 positive real roots. Therefore, the system of equations

has only the trivial solution , so .

To establish that det A0 we use induction on the size of A. We know this to be true when the size of A is 2, so assume det A > 0 whenever the size of A is at most k-1. Let be k-by-k, in which , , , and . Then expanding det A along the last row gives

But , where , so the induction hypothesis ensures that . Thus as , so . The conclusion is that is TP whenever .

3.1 SETS OF POSITIVE MINORS SUFFICIENT FOR TOTAL POSITIVITY

Given , how may it be determined whether A is TP or TN? Direct verification of the definition (calculation of minors) is dramatically complex (and prohibitive). By comparison, for verification that is a P-matrix, no better than exponential algorithms (that amount to verifying the positivity of each of the principal minors) are known to date. Fortunately, by contrast, not only do fewer than minors suffice for checking for TP, it is actually possible to check in polynomial time in n.

Since permutation of rows or columns generally alters total positivity, the cadence of index sets that determine a minor is especially important.

Definition 3.1.1 For , , , the dispersion of the index set α is .

The intent is to measure roughly how spread out the index set is relative to . If , then the index set α is called a contiguous, which we may shorten to just contiguous. If α and β are two contiguous index sets with , then the submatrix A[α, β] is called a contiguous submatrix of A and the minor is called a contiguous minor, which we may also refer to as just contiguous. A contiguous minor in which α or β is is called initial.

As an example, consider , with ; . The initial minors in this case are a₁₁, a₁₂, a₂₁, and det A. But if all the initial minors are positive, then a₂₂ must be positive as well. Then, all contiguous minors are as well. In general, the bidiagonal entries of the EB factors (and the diagonal entries of the diagonal factor) in the SEB factorization of a TP matrix may be written as ratios of products of initial minors; for example,

Before we derive formulas for the entries of the desired EB factors in general, we recall the SEB factorization by presenting it in a slightly different context.

Performing the elimination as prescribed by the Whitney ordering produces a sequence of matrices:

(3.4)

where has zeros below its main diagonal in the first t-1 columns. If we let , then the entry , is called the (i,j)-pivot of this elimination, and the number

is called the (i,j)-multiplier (see [GP92, GP96]). As described in Chapter 2, the sequence of matrices in (3.4) corresponds to the factorization

(3.5)

where D is a diagonal matrix and U is upper triangular. The purpose here in the short term is to derive formulas in terms of minors of A for the multipliers m_ij.

Consider separately the case n=4. If A is factored as in (3.5), then using the planar diagram approach derived in Section 2.6 it is not difficult to determine the following formulas for some of the multipliers:

In fact, to facilitate the proof of the general case we will make use of the planar networks associated with bidiagonal factorizations. One last observations is that if in the factorization (3.4), then assuming U is constructed with unit main diagonal, we have

for .

Proposition 3.1.2 Suppose A is factored as in (3.4). Then the multipliers m_ij, with and and j < i, are given by

Proof. First consider the case j=1. Since for each there is a unique path in the associated planar diagram from i to 1, it follows that . Hence the formula for given above follows. Now suppose j>1. In a similar spirit, notice that there is only one collection of vertex-disjoint paths from sink set to source set . We can easily derive a formula for the corresponding minor of A, which in fact is given by

Assuming the formulas in the statement of the result are true by induction on i, it follows that the product can be rewritten as

Hence combining the above formula for with the equation (3.6) we have that m_ij is equal to

Observe that similar formulas exist for the multipliers used to reduce U to diagonal form, by considering A^T in the above proposition. We omit re-writing these formulas, as they simply involve the transposes of the minors above.

This result, then, allows us to write down the SEB factorization of a square TP matrix in terms of its initial minors and to deduce that positivity of initial minors implies that a matrix is TP in the square case.

We now consider nonsquare matrices. Note that an m-by-n matrix has

initial minors and

contiguous minors.

Before we come to our next result on the sufficiency of the positivity of initial minors for checking for TP, we need a simple lemma to bridge the gap between the square and rectangular case.

Lemma 3.1.3 Suppose A is an n-by-(n+1) matrix in which all initial minors are positive. Then A can be extended to an (n+1)-by-(n+1) matrix A’ all of whose initial minors are positive.

Proof. Suppose and that the (n+1)st row of A’ has entries x_j, for . Begin with x₁. Observe that the only 1-by-1 initial minor involving x₁ is (of course) x₁, so choose x₁ arbitrarily positive. Notice that the only initial 2-by-2 minor that involves x₂ (in A’) is . Moreover, since all the initial minors of A are positive, x₂ contributes positively into this minor, x₂ can be chosen large enough so that . Continuing in this manner, since x_j enters positively into the initial minor , it follows that x_j can be chosen large enough to ensure this initial minor is positive. This completes the proof.

The next result has appeared often in recent times (according to [FZ00] it first appeared in [GP92b]), and can also be found in [GP96, Thm. 5.2].

Theorem 3.1.4 If all initial minors of are positive, then A is TP.

Proof. Use Lemma 3.1.3 to extend A to a square matrix A’, with all the initial minors of A’ are positive. Then by the remarks preceding Lemma 3.1.3 it follows that A’ is TP, and hence A is TP.

Since the initial minors are contained among the contiguous minors, positivity of the latter implies positivity of the former and, thus, total positivity. This gives the classical result due to Fekete [Fek13] as a corollary.

Corollary 3.1.5 If all contiguous minors of are positive, then A is TP.

We can extend this idea of the sufficiency of checking just the contiguous minors to the class TP_k.

Corollary 3.1.6 Suppose A is an m-by-n matrix with the property that all its k-by-k contiguous submatrices are TP. Then A is TP_k.

Proof. Applying Corollary 3.1.5 we have that any submatrix of the form or consisting of k consecutive rows or k consecutive columns of A is TP. Now consider any collection of k rows of A, say, . Note that any k-by-k contiguous submatrix of B must lie in some collection of k consecutive columns of A. Hence, this submatrix of B must be TP. Thus every k-by-k contiguous submatrix of B is TP, and therefore, by Corollary 3.1.5, B is TP. A similar argument may be applied to any collection of k columns of A. From this we may conclude that every k-by-k submatrix of A is TP, and hence A is TP_k.

Corollary 3.1.7 Suppose A is an m-by-n matrix. If all the initial minors of A up to size k-1 are positive and all its k-by-k contiguous minors are positive, then A is TP_k.

We note that the initial minors form a minimal set of minors whose positivity is sufficient for total positivity.

Example 3.1.8 The positivity of no proper subset of the initial minors is sufficient for total positivity. Any of the minors being positive allows the remaining minor to be chosen negative.

Nonetheless, there are other subsets of minors, noncomparable to the initial minors, whose positivity is sufficient for total positivity. Minimal such sets have been identified in [FZ99, Thm 4.13] (and in [BFZ96] for analogous criteria involving triangular matrices).

In the event that it is somehow known that is TN, positivity of a smaller set of minors is sufficient for total positivity.

Definition 3.1.9 An upper right (lower left) corner minor of is one of the form in which α consists of the first k (last k) and β consists of the last k (first k) indices, . A corner minor is one that is either a lower left or upper right minor.

We note that there are 2n-1 distinct corner minors in .

Theorem 3.1.10 Suppose that is TN. Then A is TP if and only if all corner minors of A are positive.

Proof. Clearly if A is TP, then the corner minors of A are positive. So assume that A is TN and the corner minors of A are positive. If, in addition, the initial minors of A are also positive, then A is TP by Theorem 3.1.4. So assume that some initial minor of A is zero, say . Then observe that is principal in the (corner) submatrix . So by Fischer’s determinantal inequality (see Section 6.0) this corner minor must be zero, which is a contradiction. Hence all initial minors of A must be positive, and thus A is TP.

In case , , the corner minors need not include all entries of A, and thus Theorem 3.1.10, is not valid in the nonsquare case. What additional minors are needed?

Definition 3.1.11 If , we call any minor that is either a corner minor or an initial minor with a maximal number of rows and columns () a generalized corner minor.

One may think of sliding the maximal corner minors to the left/right in case m<n.

Theorem 3.1.12 Suppose is TN. Then A is TP if and only if all generalized corner minors of A are positive.

Proof. The proof is by induction on n (assuming ). If n=m, then the result holds by Theorem 3.1.10. Suppose A is m-by-n. Observe that since the corner minor and A is TN, it follows from Fischer’s determinantal inequality (see Section 6.0) that

and

and Applying the same reasoning to implies . Continuing in this manner proves that all proper corner minors of

are positive. Furthermore, the m-by-m corner minor of

is positive since all maximal contiguous minors are assumed positive. So by induction is TP. To prove that A is TP we must show that all contiguous minors that include column n are positive. Observe that every such minor is a principal minor of some corner minor, which by assumption is positive. So, by Fischer’s determinantal inequality, each of these minors are positive. Hence A is TP.

For completeness, we offer a different proof of Theorem 3.1.10, one from a combinatorial point of view.

“Suppose that A is TN. Then A is TP if and only if all corner minors of A are positive.”

Proof. Since A is nonsingular and TN, A can factored as in (2.12), where the parameters l_i and u_j are nonnegative. Moreover, since A is assumed to be invertible, it follows from Fischer’s inequality that each , as they can be written as ratios of products of principal minors of A. Consider the following figure (see Figure 3.1) which corresponds to the planar diagram corresponding to lower triangular part of (2.12). Since the (n,1) entry of A is positive, by assumption, there exists a path from n to 1 in Figure 3.1. This implies that all the weights of the edges along the first stretch from n down to 1 must be positive, as this represents the only possible such path. Similarly, since , it follows that the weights of the edges that make up the second stretch from n down to 2 must all be positive. Continuing inductively using , it follows that each such edge weight in the lower triangular part of (2.12) is positive. Similarly, the weights of the edges corresponding to the upper triangular part of (2.12) may also be shown to be positive.

Figure 3.1 Diagram corresponding to A

Observe that for any corner minor of the form , there is a unique collection of vertex-disjoint paths in . As demonstrated in the proof of Theorem 3.1.10, all edges appear at least once in the union of collections of paths in over all corner minors , and, more important, there is at least one edge that appears in that does not appear in for each other corner minor . Hence if some corner minor is omitted, it follows that the weight of at least one edge is unaccounted for, and therefore it may be zero. However, by Theorem 2.6.2, the corresponding matrix is not TP. Thus no subset of the list of corner minors suffices as a test for total positivity.

3.2 APPLICATION: TP INTERVALS

We turn to an application of our criteria to study “intervals” “between” TP matrices. We use <, ≤ to denote the usual entrywise partial order on matrices; that is, for , , means , for all i,j.

Example 3.2.1 If and are TP, then not all matrices in the interval between A and B need be TP; that is, if , then C need not be TP. Let

Then A, B are TP and

satisfies . But, C is not TP.

There is, however, a partial order on real matrices for which the interval between two matrices that are TP consists only of TP matrices.

Definition 3.2.2 The “checkerboard” partial order on real matrices is defined as follows. Recall from Section 1.3 that S_k denotes the k-by-k signature matrix whose diagonal entries alternate in sign beginning with +: for example,

For , we write if and only if and if and only if .

This means that the entries in positions, the sum of whose indices is even, are aligned in the usual way and that order is reversed in the “odd” positions.

Lemma 3.2.3 If , , and A and B are TP, then .

Proof. If , and A and B are TP, then it follows that and that both are inverse positive. Let with similar meanings applied to , and so on. To complete a proof of this lemma, we need an auxiliary result relating semipositive matrices and inverse positive matrices. Suppose F and G are two n-by-n matrices such that , , and assume there exists a vector x>0 with . Then . Given the conditions on F and G above, it is clear that . Thus must be a Z-matrix (see [HJ91]). Using the fact that there exists a vector x>0 with , it follows that . Hence must be an M-matrix (see [HJ91, Sect. 2.5]). Thus . Finally, since , we have that .

Now to complete the proof of the lemma, let and in the claim above. Let x be the unique vector that satisfies , where e is the vector of all ones. Then since is inverse positive, x>0. Further we have . Hence the hypotheses of the claim are satisfied, and so we conclude that is inverse positive. Hence any matrix C, such that , must be invertible and since A and B are TP, it follows that, in fact, .

We note here that this lemma also appeared in [Gar96], in which the proof contained a reference to an article on monotone matrices. A square matrix is monotone if and only if it is inverse nonnegative. The proof we presented above is an adaptation of the one used in [Gar96] and the subsequent reference, but since it is sufficiently different and requires fewer technical results, we decided to include it for completeness.

Theorem 3.2.4 If , , and A and B are TP, then C is TP.

Proof. It suffices, by Theorem 3.1.4, to show that the initial minors of C are positive. But if C is an initial minor of C and are the corresponding initial minors of A, B, respectively, then it follows that either or holds depending on the relative position of the initial minor. However, in either case Lemma 3.2.3 applies and . Hence C is TP.

Example 3.2.5 We note that, if TP is replaced by TN, then Theorem 3.2.4 no longer holds. For example,

however, both end matrices are TN, while the middle matrix is not. The difficulty is that zero lines have been inserted in such a way that the partial order reverts to the usual partial order ≤.

In the intermediate case, it is not known whether Theorem 3.2.4 remains valid when TP is replaced by InTN.

3.3 EFFICIENT ALGORITHM FOR TESTING FOR TN

Returning now to sufficient sets of minors, we have, thus far, considered the TP case in detail. What about sets of minors whose nonnegativity is sufficient for TN? Unfortunately, the situation is rather different.

Example 3.3.1 For positive integers m and n and any index sets α, β, , there is an such that every minor of A is nonnegative, except that . To see this choose a k-by-k matrix for which all proper minors are nonnegative, but the determinant is negative. Place this matrix in the α, β positions of an m-by-n matrix all of whose remaining entries are 0. Such an A has the desired features.

If the rank of A is known, however, some reduction in the collection of minors needed to test for total nonnegativity is possible.

Theorem 3.3.2 If and rank, then A is TN if and only if for all index sets α, β, such that and , .

As the proofs of this theorem are rather long and technical, we will only provide a brief discussion highlighting the key aspects of the arguments given in [And87, Thm. 2.1] and [Cry76, Thm. 1.3].

Both proofs rely on induction and both assume that all minors up to size k-1 have been shown to be nonnegative. (Note that the base case, namely k=1, follows since all 1-by-1 minors satisfy .) Then the argument proceeds by assuming that there is a minor of size k that is negative. Moreover, such a k-by-k minor is chosen such that is minimal, assuming β is the column set of this minor. Clearly, by hypothesis, and . The latter inequality is essential for reaching a contradiction.

At this point both Ando and Cryer appeal to “Karlin’s identity” (see Chapter 1 (1.6)) to link minors whose column sets have dispersion l to minors whose column sets have dispersion l-1 (keeping in mind the minimality of l above).

Ando reaches a contradiction by employing Sylvester’s determinantal identity and the inequality to verify that rank.

Cryer, on the other hand, obtains a contradiction by instead appealing to an auxiliary result (see [Cry76, Lemma 3.1]) on ranks of certain TN matrices.

We note that Theorem 3.3.2 could be applied to A^T to give the sufficiency of the minors with .

Definition 3.3.3 A minor of is quasi-initial if either and β, , is arbitrary or α, , is arbitrary, while , .

In the case of triangular matrices the following result holds (see [And87, Cry76, GP93B]). Notice that only half of the quasi-initial minors are required given the triangular form.

Lemma 3.3.4 Suppose is invertible and lower triangular. Then L is InTN if and only if

for all .

Proof. Suppose with . Let and assume that and . If , then , since L is lower triangular. If and , then , by hypothesis. Finally, suppose and . Let . Then

by hypothesis. Moreover, since L is lower triangular

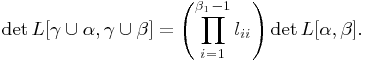
Since L is invertible, for all i, hence . By Theorem 3.3.2, L is InTN. The converse is trivial.

The fact that all InTN matrices have factorizations into lower and upper triangular InTN matrices is needed along with the above fact to prove the next result for general InTN matrices.

Theorem 3.3.5 If is invertible, then A is InTN if and only if the leading principal minors of A are positive and all quasi-initial minors of A are nonnegative.

Proof. If the leading principal minors of A are positive, it follows that A can be written as A=LDU, where D is a positive diagonal matrix and L (U) is a lower (upper) triangular matrix with unit main diagonal. Applying the Cauchy-Binet identity to the product LDU we have

Since D is a positive diagonal matrix, it follows that , for any . Hence, by Lemma 3.3.4, L is InTN. Similarly,

Again it follows that for any . Hence, by Lemma 3.3.4, U is InTN. Thus if L, D, and U are all InTN, then A=LDU must be InTN.

Recall that in [GK02] the term quasi-principal was used in conjunction with their investigations on criteria for a matrix to be oscillatory. Our definition is different from the one used in [GK02], and our intention is also different. This notion of quasi-principal was needed to verify that if an n-by-n matrix is oscillatory, then its (n-1)st power will be TP (see [GK02, Ch. 2]).

The sufficient sets of minors we have discussed are of theoretical value, and they do not lead to the most efficient (or simple) methods to check for total positivity or total nonnegativity, even when some advantage is taken in the overlap of calculation of different minors (as in [GM87]). Here, we restrict attention to the case of square matrices. Via calculation to produce an LU factorization, total positivity or total nonnegativity may assessed in O(n³) effort for . In fact, the SEB factorization may be calculated in O(n³) time if A is InTN.

Consider then the process of reducing a full matrix A to upper triangular form via Whitney elimination, beginning by eliminating the lower left entry with the one above, continuing up the column, then moving to the next column to the right, and so on. Once an upper triangular matrix is produced, the same process is applied to its transpose to reduce to diagonal form. At each step, a multiple of one entry is subtracted from that below it (to produce a zero). This multiplier will end up as the off-diagonal entry in one of the TN EB factors of the SEB factorization. If no entry prematurely becomes zero and all multipliers are positive, then the original A was TP. If A is invertible and no multiplier is negative, then A is InTN.

For singular TN matrices, it may happen that a zero entry appears before a nonzero. In this event, the entire row in which the zero lies must be zero and that row may be ignored and a nonzero row above it can be used in the elimination process (see also Chapter 2, Section 3). Again, allowing for zero rows, if no negative multiplier is encountered, or if a zero entry above a nonzero entry without the row being zero, the matrix is not TN.

We provide some illustrative examples to bring together the above discussion.

Example 3.3.6 The first illustration is meant to indicate that when reducing a singular TN matrix, a scan of the rows is necessary to detect whether the original matrix is TN. Consider the following sequence of eliminations up the first column.

At this point the algorithm is stopped, as we have encountered a zero (pivot) above a nonzero in the same column, and on further examination the corresponding row is not zero. If we had continued with the elimination, albeit not with TN bidiagonal matrices, we would end up with the InTN matrix

The second illustration is intended to demonstrate that reduction of singular TN matrices need not always produce zero rows (at least to triangular form).

Observe that in this case all the multipliers used in reducing this matrix to triangular form are positive.

The ideas developed thus far allow characterization of the zero/nonzero patterns possible in a TN matrix and, more generally, the possible arrangements of singular minors. In the event of an InTN matrix, the zero patterns, and so forth are more limited.