Chapter Seven

Row and Column Inclusion and the Distribution of Rank

7.0 INTRODUCTION

Recall that an m-by-n matrix A is said to be rank deficient if

Just as with zero entries (see Section 1.6), the distribution of ranks among submatrices of a TN matrix is much less free than in a general matrix. Rank deficiency of submatrices in certain positions requires rank deficiency elsewhere. Whereas, in the case of general matrices, rank deficiency of a large submatrix can imply rank deficiency of smaller, included submatrices, in the TN case rank deficiency of small submatrices can imply that of much larger ones. To be sure, in the general m-by-n case, a p-by-q submatrix of rank r does imply that the rank of the full m-by-n matrix is no more than , so that rank deficiency of submatrices can imply rank deficiency of larger matrices. But, in the TN case a small rank deficient submatrix can imply that a much larger matrix has no greater rank, just as a zero entry can imply that other entries and entire blocks are zero.

Another, related phenomenon will be of interest here. Recall that in a positive semidefinite matrix, even if a principal submatrix is singular, any column outside it, but lying in the same rows, is in its column space (see, for example, [Joh98]). Thus, adding such columns cannot increase the rank, relative to that of the principal submatrix. Though principality of submatrices is less important in the TN case, there is a related phenomenon in the TN case, which is the subject of the next section. This phenomenon will be used later to develop general statements about the possible ranks of submatrices.

In the following sections we also show that, under a mild regularity assumption, the rank of a TN matrix must be concentrated in a single, contiguous, nonsingular, square submatrix (the “contiguous rank property”).

7.1 ROW AND COLUMN INCLUSION RESULTS FOR TN MATRICES

It is known that if is positive semidefinite, then any column vector of the form

must lie in the column space of the principal submatrix . This classical fact may be seen in a variety of ways. For example, consider a Hermitian matrix of the form

If the column vector c is not in the range of B, null space/range orthogonality implies there is a vector x in the null space of B such that . There is then an such that

Since A^T is also positive semidefinite, there is an analogous statement about rows. Moreover, for positive semidefinite matrices (though both inclusions are valid), it is equivalent to say that for each j either the row lies in the row space or the column lies in the column space of the indicated principal submatrix. It is precisely this statement that may be substantially generalized. The above fact has been known to several researchers for some time; see [Joh98] for more history and motivation.

For a given m-by-n matrix A, we let () denote the row (column) space of A. Then .

Let () denote the set of n-by-n (P-) matrices which also satisfy Fischer’s inequality (see Section 6.0). The class contains many familiar classes of matrices, for example, positive semidefinite matrices, M-matrices, TN matrices (and their permutation similarities) and triangular matrices with nonnegative main diagonal.

Using the notation developed above, we may reformulate the column inclusion result for positive semidefinite matrices as follows: If A is an n-by-n positive semidefinite matrix, then for any and for each j,

The next result can be found in [Joh98, Thm. 6.1].

Theorem 7.1.1 If and is such that , then for each j either or .

Some condition imposed upon rank() is necessary, as may be seen from the following example.

Example 7.1.2 Let

Then . Let . Then . However, and .

Note the above matrix is a reducible TN matrix. To generalize further, we use the following concept.

Definition 7.1.3 An n-by-n matrix A satisfies the principal rank property (PRP) if every principal submatrix A’ of A has in turn an invertible rank(A’)-by-rank(A’) principal submatrix.

The following is simply a recasting of the previous definition. A satisfies the PRP if for every α, there exists , with so that is invertible.

Observe that the PRP is inherited by principal submatrices. The next lemma gives a sufficient condition for a matrix to satisfy the PRP.

Lemma 7.1.4 Let A be an n-by-n matrix. Suppose the algebraic multiplicity of 0 equals the geometric multiplicity of 0, for every principal submatrix of A. Then A satisfies the PRP.

Proof. Let A’ be any k-by-k principal submatrix of A. If A’ is nonsingular, then there is nothing to do. Thus suppose (). Since the algebraic multiplicity of 0 equals the geometric multiplicity of 0 for A’, it follows that the characteristic polynomial of A’ is equal to

in which . Since s_r is equal to the sum of all the r-by-r principal minors of A’, it follows that there exists at least one nonsingular r-by-r principal submatrix of A’. This completes the proof.

Note that symmetric matrices are examples of matrices that satisfy the above lemma, and hence satisfy the PRP. The converse to the above general lemma is easily seen not to hold in general. The simplest example demonstrating this fact is

However, for P₀-matrices the condition given in the lemma is clearly also necessary, since for a P₀-matrix the coefficient s_r will be nonzero if and only if there is a nonsingular r-by-r principal submatrix of A. The following is found in [Joh98, Thm. 6.5].

Theorem 7.1.5 If satisfies the PRP, and , then for each j either or .

Theorem 7.1.5 has two hypotheses: and PRP. Neither of these can be omitted in general. For example,

satisfies PRP but not the row or column inclusion conclusion of Theorem 7.1.5, and

is in , does not satisfy PRP, and does not satisfy the conclusion of Theorem 7.1.5 for .

Since any positive semidefinite matrix satisfies the PRP (by the previous lemma) and is in (see [HJ85]) we have the following.

Corollary 7.1.6 If A is an n-by-n positive semidefinite matrix, then for any and for each j,

We now specialize to the class of TN matrices, a subclass of . We may extend our row or column inclusion results somewhat to non-principal submatrices for this class. Before we state our next result, we need the following notation. Let and let be the elements of arranged in increasing order, and let be the elements of arranged in increasing order. Define , , and . For , let denote the submatrix of A obtained from by inserting any row s for which . Similarly, let denote the submatrix obtained from by inserting any column q for which .

Theorem 7.1.7 Let A be an n-by-n TN matrix and let , with . Suppose that , and either or at least one of or . Then either

or

for .

Proof. Let , with . First suppose . The case when will then follow by transposition. Let , with and (if such s, q exist). The case in which and is handled similarly. Assume for the purpose of contradiction that and . Consider the submatrix , which is TN and has rank equal to . Thus there exists a nonsingular submatrix A’ of of order . Since the , it follows that , in which , and , . Furthermore, is principal in A’, since and . Observe that since , is singular. Consequently,

This is a contradiction and hence the conclusion holds.

Finally, suppose , and let . Define and . Let t be any fixed integer, . Assume there exist a row indexed by s, , and a column indexed by q, , in which and . In fact, both must equal . Then . Again consider the nonsingular submatrix A’ of , which (as before) must be of the form . Applying arguments similar to those above, we arrive at a contradiction. This completes the proof.

We complete this discussion with an example that illustrates three possibilities. The first two give insight into the necessity of the hypotheses in Theorem 7.1.7. The final one illustrates the previous remark.

Example 7.1.8 Let

It is not difficult to determine that A is TN. (i) Let and . Then . However, if we let s=1 and q=5, then and . Thus, it is necessary to include a row and a column from the same “gap” in α and β. (ii) Similar arguments can be applied in the case and , and with . (iii) Let and . Suppose q=2. Then

Recall that a submatrix of a given matrix is called contiguous if both its rows and columns are based on consecutive sets of indices; sometimes such a matrix is called a block. A submatrix that extends a contiguous one by keeping the same rows (columns) and adding all earlier or later columns (rows) is called a swath. Figure 7.1 depicts two of the swaths determined by the swath B. A right (lower) swath determined by B includes B and the columns (rows) to the right (below). Left and upper swaths are defined similarly.

Figure 7.1 Swaths of a block B

Theorem 7.1.9 Suppose that is an m-by-n TN matrix and that A[α, β] is a contiguous rank deficient (and not necessarily square) submatrix of A. Then, for each index i greater than those in α and each index j greater than those in β (and for each index i less than those in α and each index j less than those in β), either

or

Proof. It suffices to prove one of the two claims, as the other is similar. We prove the first. Suppose the claim is not true. Let . Then

Hence the matrix on the left contains a -by- submatrix B that is InTN. The matrix B must include the last row and column, because , so that the submatrix A’ of A[α, β] that lies in B must lie principally in B. Application of Fischer’s determinantal inequality (6.3) to B implies that any principal submatrix of B is also invertible. In particular, A’ is. But, as A’ is -by-, its invertibility implies that , a contradiction that completes the proof.

Corollary 7.1.10 Suppose that A is an m-by-n TN matrix and that A[α, β] is a contiguous, rank deficient (and not necessarily square) submatrix of A. Then either the right or lower swath determined by A[α, β] has the same rank as A[α, β], and either the left or upper swath determined by A[α, β] has the same rank as A[α, β].

Proof. Again, it suffices to prove one of the two conclusions, as the other is similar. Consider the first. Unless both the right and lower swaths have the same rank as A[α, β], one, say the right, has greater rank, and thus there is a vector outside A[α, β] that is not in . Using this identified vector and Theorem 7.1.9 implies the desired conclusion.

We note as a final remark that if A[α, β] in Corollary 7.1.10 is of full rank, then the same conclusions trivially hold.

7.2 SHADOWS AND THE EXTENSION OF RANK DEFICIENCY IN SUBMATRICES OF TN MATRICES

In the case of a zero entry in a TN matrix, a “shadow” of zero entries is cast to the northeast or southwest, unless the initial zero entry happens to lie on a zero line (see Section 1.6). For purposes of generalization, the zero entry may be viewed as a rank deficient 1-by-1 block, and a zero line as failure of a 1-regularity hypothesis. What, then, are the appropriately more general statements (both the regularity hypothesis and conclusion) when a larger, rank deficient submatrix is encountered?

Definition 7.2.1 Let and , with and , and let A be an m-by-n matrix. Define and . Then the convex hull of the submatrix A[α, β], denoted by , is the submatrix , that is, the submatrix with all intermediate rows and columns filled in.

Consider the following example. Let

and suppose and . Then

and

Definition 7.2.2 A shadow of a contiguous submatrix of a matrix A is either the convex hull of its upper and right swaths (northeast shadow) or the convex hull of its lower and left swaths (southwest shadow).

For example, if A is the 4-by-6 matrix above, then the southwest shadow of is given by,

Our principal purpose here is to show that, under appropriate regularity conditions, in a TN matrix A, if B is a rank deficient noncontiguous submatrix of A, then the rank of its convex hull can be no greater than (and, thus, will be equal to ) and that if B is a contiguous, rank deficient block, then the rank of one of its shadows will be no greater. To accomplish this, some further structure must be developed and thus may be of independent interest. We do note that others have studied rank deficiency in TN matrices and have considered the concept of shadows, along with other notions. For example, in [GK02] a number of interesting results were proved on the rank of a TN matrix, based on the ranks of “initial” and “trailing” rows (see, for example, [GK02, Lemma 2, p. 98]), which we actually state and use later in this section. More recently, rank deficient blocks and shadows have been observed in the context of TN matrices. See [BP82], where it seems the term shadow was first used, and consult [Pin08] for some recent work on rank deficient submatrices of TN matrices, which overlaps part of the development here.

The next result is a reformulation of a similar lemma proved in [GK02, p. 98].

Lemma 7.2.3 Suppose A is an m-by-n TN matrix that is the convex hull of rows , and that the rank of the matrix consisting of these rows is deficient. If rows are linearly independent and rows are linearly independent, then .

Proof. For convenience we set , and let r_i denote the ith row of A. Then there exist scalars (not all of which are trivial) such that

Furthermore, by hypothesis . Let r_j be any other row of A (necessarily ). Consider the p-by-p submatrix of A, , where β is any collection of p columns. Then

by the multilinearity of the determinant. On the other hand, there must exist a collection of p-1 columns γ such that by hypothesis. Hence

from which it follows that . From above we conclude that , for each such j. Hence r_j must be a linear combination of the rows . Thus we have shown that .

The next lemma may be viewed as a substantial constraint on line insertion in a rank deficient TN matrix. However, it is convenient to state it slightly differently.

Lemma 7.2.4 Suppose that A is an m-by-n TN matrix such that rows form a linearly independent set and rows form a linearly independent set, while the rank of the matrix formed by rows is m-2. Then, , as well.

Proof. The proof applies Lemma 7.2.3. Under the hypothesis, 0 is a nontrivial linear combination of rows that is unique up to a factor of scale. In this linear combination, there must be a nonzero coefficient among the first k-1 and among the last , else either the first k-1 or the last would constitute a linearly dependent set, contrary to hypothesis. Let r, , be the index of the first nonzero coefficient and s, , be the index of the last. Since deletion of any row with a zero coefficient in the nontrivial linear combination must leave a linearly independent set of rows, rows , except for k (), satisfy the hypothesis of Lemma 7.2.3. Application of Lemma 7.2.3 implies that rows (including k) are rank deficient by 2 and, thus, that A is rank deficient by 2, as was to be shown.

Consider the following illustrative example. Using the notation in the lemma above, we let m=4 and k=3. Suppose A is a TN matrix of the form

where the third row is to be determined. Observe that, as presented, A satisfies the hypotheses of Lemma 7.2.4 with m=4 and k=3. Then the only way to fill in the third row and preserve TN is if this row is a linear combination of rows 1 and 2 (the details are left to the reader).

We also note that in the case of TP matrices, a row may be inserted in any position so as to increase the rank, that is, to preserve TP (see Theorem 8.0.2).

We now turn to consideration of the consequences of a dispersed (not contiguous) rank deficient submatrix. Our purpose is to understand the circumstances under which its rank limits that of the smallest contiguous submatrix containing it. For this purpose, we need a hypothesis that extends the tight one used in Lemma 7.2.4.

Definition 7.2.5 Let A[α, β] be a dispersed submatrix of A, and suppose that and , in which each and is a consecutive set of indices, while () is not, (). We call () the contiguous components of α (β). Now, we say that A[α, β] satisfies the partitioned rank intersection (PRI) property if, for each i, (and ), the span of the rows (and columns) of (and ) has a nontrivial intersection with the span of the rows of (and ). By convention, we also say that any contiguous submatrix satisfies the PRI property.

Observe that the 4-by-5 matrix A above in the previous example satisfies PRI with .

Theorem 7.2.6 Let A be an m-by-n TN matrix and let A[α, β] be a submatrix of A such that . If satisfies PRI, then

as well.

Proof. The proof is based upon multiple applications of Lemma 7.2.4. First, we note that we may consider only the case in which the column index set has only one contiguous component, as when this case is proven, we may turn to the columns, under the assumption there is only one component to the row index set. Now we consider the gaps between row contiguous components one at a time. Without loss of generality, we may assume that our gap consists of just one row and that the rows falling in other gaps have been deleted. We are not yet in the case covered by Lemma 7.2.4, but we may obtain this case by (possibly) deleting some rows above and/or some rows below the gap. If, say, the rows above the gap are not linearly independent, then rows may be deleted from among them so as to leave a linearly independent set with the same span. Similarly, rows from below may be deleted, if necessary. The (nontrivial) overlap it spans will not have changed. If it has dimension greater than 1, then further rows may be deleted from above or below, until the hypothesis of Lemma 7.2.4 is achieved. Once it is, and Lemma 7.2.4 is applied, any deleted rows may be reintroduced without increasing rank. Continuing in this way for each row gap (and each vector in that gap), as well as for the columns, proves the claim of the theorem.

A straightforward way to see that a condition like PRI is necessary is to note that line insertion into a TP matrix is always a possibility (see Theorem 8.0.2), so as to preserve the property of being TP, and hence increasing the rank.

A nice illustration of the convex hull result above can be seen in the next example. Suppose A is a 4-by-4 TN matrix of the form

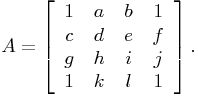
Assuming A has no zero lines (which does not affect the conclusion), which then will imply that A has no zero entries, we wish to conclude that A has rank equal to 1. Two applications of Sylvester’s identity (1.4) applied to the principal submatrices and yield

Finally, it is easy to verify that e=bc and h=ag, and thus A is a rank one TN matrix. Observe that A above satisfies PRI.

Though a rank deficient submatrix of a TN matrix gives no general implication about a specific submatrix that extends outside of it, there is a remarkably strong “either/or” implication about possibly much larger submatrices that lie in one of its shadows.

Definition 7.2.7 Given an m-by-n matrix A, the two sections determined by a submatrix A[α, β] are the submatrices , the latitudinal section, and , the longitudinal section; the former is just the rows α and the latter is just the columns β. If A[α, β] is rank deficient, it is said to satisfy the section rank property, SRP, if each of its two sections have greater rank. Note that if A[α, β] is just a zero entry, this means that this zero entry does not lie on a zero line.

Keeping in mind the notions of sections and shadows, we introduce some further notation. If A is an m-by-n matrix and A[α, β] is a fixed contiguous submatrix of A with and , then the northeast shadow of A (that is, the convex hull of its upper and right swaths) will be denoted by , where and . Similarly, the southwest shadow of A[α, β] will be denoted by .

Theorem 7.2.8 Suppose that A is an m-by-n TN matrix and that is a contiguous, rank deficient submatrix satisfying the SRP. Then either its northeast shadow () or its southwest shadow () has the same rank as A[α, β]. Moreover, which actually occurs is determined by which of the swath ranks exceeds .

Proof. The first statement in the theorem above will follow from two applications of the general row and column inclusion result (Theorem 7.1.9). Since A[α, β] satisfies SRP, there exists a column in , not in positions β, that is not in the column space of ; or there is a column in , not in positions β, that is not in the column space of . Suppose, without loss of generality, this column lies in , and call it x. In a similar fashion we identify a row, y^T, not in the row space of , that lies in, say, positions . In this case, any row z^T in must lie in the row space of by an application of Theorem 7.1.9. Thus .

Now, we repeat the above argument with replaced by . Let u be any column lying in rows and in . Then, by Theorem 7.1.9, taking into account that y^T is not in the row space of , we conclude that u must lie in the column space of . Hence we have shown ; that is, the southwest shadow of has no larger rank.

Observe if and , then we may deduce, via similar arguments, that . Finally, we note that the case and or and cannot occur, as they violate general row and column inclusion (see Theorem 7.1.9).

As an illustration, consider the following TN matrix. Let

Observe that A does not satisfy the SRP, as the longitudinal section of the has rank 1, but the latitudinal section has rank 2. Furthermore, observe that both the northeast and southwest shadows of also have rank equal to two, greater than the rank of .

Corollary 7.2.9 Suppose A is an m-by-n TN matrix and that is a rank deficient submatrix satisfying PRI and such that satisfies the SRP. Then, either the northeast shadow of or the southwest shadow of has the same rank as A[α, β].

Proof. Since A[α, β] satisfies PRI, we know that (by Theorem 7.2.6). Furthermore, since is assumed to satisfy SRP, by Theorem 7.2.8 the desired conclusion follows.

Corollary 7.2.10 Suppose that A is an n-by-n InTN matrix and that is a rank deficient submatrix. If is contiguous, then one of its shadows has rank equal to that of (in particular, the one to the side of the diagonal of A on which more entries of A[α, β] lie). If is not contiguous, but satisfies PRI, then one of the shadows of has the same rank as (in particular, the one to the side of the diagonal of A on which more entries of lie). In neither case can both shadows have the same rank as .

7.3 THE CONTIGUOUS RANK PROPERTY

Our purpose here is to show that in a TN matrix the rank can be “explained” by a contiguous submatrix, given a necessary but simple regularity condition.

Definition 7.3.1 An m-by-n matrix A obeys the contiguous rank property, CRP, if it contains a contiguous -by- submatrix whose rank is equal to .

Example 7.3.2 The matrix

is TN, and . But A does not enjoy the CRP, as each of its four 2-by-2 contiguous submatrices has rank 1. The difficulty is the zero row, which interrupts the submatrix

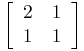
of rank 2.

A regularity condition that rules out zero lines and additional degeneracies is the following.

Definition 7.3.3 An m-by-n matrix of rank at least r is called -regular if any submatrix of r-1 consecutive lines (either r-1 full, consecutive rows or columns) has rank r-1.

Of course, 1-regularity may be viewed as a strengthening of the “no zero-lines” hypothesis in Theorem 1.6.4 on zero/nonzero patterns of TN matrices. In some situations, this is the appropriate hypothesis.

Our main result of this section is then

Theorem 7.3.4 Every -regular, TN matrix of rank r satisfies the CRP.

Proof. We first show that there exist r consecutive columns whose rank is r. Consider the first r-1 columns. They have rank r-1 by hypothesis. If the next column is not a linear combination of these, the first r columns are our desired consecutive columns. If the next column is a linear combination of the first r-1 columns, consider columns 2 through r, which then must have the same span as the first r-1 columns. Continue in this manner until a column, not in the span of the first r-1, is encountered (there must be such a column as the rank is r). This column, together with r-1 columns preceding it, will be the desired r consecutive columns of rank r.

We next show that within the above found r consecutive linearly independent columns, there are r consecutive rows that are linearly independent, thus determining the desired square, nonsingular r-by-r contiguous submatrix. To accomplish this, we make use of the shadow result (Theorem 7.2.8) to show that the above r columns will also satisfy -regularity (on the rows); note that it is not immediate that this hypothesis on the full matrix conveys to our r columns. Then the argument of the first paragraph applied to the rows of our r columns will identify the desired nonsingular r-by-r block.

Suppose, for the sake of a contradiction, that the r consecutive columns of rank r, call them A’, do not satisfy r-1 regularity with respect to the rows. Thus there exists a collection of r-1 consecutive rows in A’ that is not of full rank. Starting from the bottom of A’ and considering collections of r-1 consecutive rows, let B be the first such collection of r-1 consecutive rows of rank less than r-1. Suppose B occurs in rows and . Since, in A, rows have rank r-1, there must be a column, x, outside A’ in these rows, not in the span of B. Since there is a row below B in A’ not in the row space of B, we conclude by row and column inclusion (Theorem 7.1.9) that this column must occur in the left swath of B. Hence, applying Theorem 7.1.9 again we have that the rank of the northeast shadow of B is the same as the rank of B (that is, the northeast shadow of B has rank less than r-1). It now follows that the submatrix of A’ consisting of all columns and the bottom rows is (r-1)-regular. Observe that this submatrix has at least r rows, as . If the submatrix B occurs in rows and , then we arrive at a contradiction, by following similar arguments, in that we may conclude the rank of A’ is at most r-1. Observe that a similar argument may be applied from the top of A’ to yield similar conclusions.

From the above analysis, we may assume that the only rank deficient collections of r-1 consecutive rows of A’ occur in the first r-1 rows or the last r-1 rows. In this case, the submatrix obtained from A’ by removing the first and last row will satisfy (r-1)-regularity. Now repeat the argument from the first paragraph to identify the desired nonsingular r-by-r block.

Example 7.3.5 Suppose A is a 3-by-3 TN matrix of the form

Assuming that the rank of A is 2 and that A is 1-regular, we know that none of can be zero. Now, if A does not satisfy CRP, then each of its four 2-by-2 contiguous submatrices are of rank 1, from which we may conclude that a=e and d=b. Thus A must be of the form

This leads to a contradiction as c must then be equal to both ab and , which can only occur if all .