Chapter Eight
![]()
Hadamard Products and Powers of TN Matrices
8.0 DEFINITIONS
The Hadamard product of two m-by-n matrices ![]() and
and ![]() is defined and denoted by
is defined and denoted by
![]()
Furthermore, if A is a m-by-n and entrywise nonnegative, then ![]() denotes the tth Hadamard power of A, and is defined to be
denotes the tth Hadamard power of A, and is defined to be
![]()
for any ![]() .
.
Evidently, if A and B are entrywise positive (that is, TP1), then ![]() is also TP1. Furthermore, with a bit more effort it is not difficult to demonstrate that if A and B are TP
is also TP1. Furthermore, with a bit more effort it is not difficult to demonstrate that if A and B are TP![]() and 2-by-2, then
and 2-by-2, then
![]()
as both det A and ![]() are positive.
are positive.
From the above simple inequality we are able to draw two nice consequences. The first is that TP![]() or TN
or TN![]() matrices are closed under Hadamard products. The second is that if A and B are both TP (or TN) and
matrices are closed under Hadamard products. The second is that if A and B are both TP (or TN) and ![]() , then
, then ![]() is TP (TN). Unfortunately, TP (TN) are not closed under Hadamard multiplication in general (see [Joh87, Mar70]).
is TP (TN). Unfortunately, TP (TN) are not closed under Hadamard multiplication in general (see [Joh87, Mar70]).
For example, consider the 3-by-3 TN matrix,
 |
(8.1) |
Then ![]() is TN
is TN![]() , but
, but ![]() , so
, so ![]() is not TN. Similarly, TP is not closed under Hadamard multiplication, and it is straightforward to deduce that nonclosure under Hadamard multiplication extends to the m-by-n case, as both classes TP and TN are inherited by submatrices.
is not TN. Similarly, TP is not closed under Hadamard multiplication, and it is straightforward to deduce that nonclosure under Hadamard multiplication extends to the m-by-n case, as both classes TP and TN are inherited by submatrices.
Nonclosure, under Hadamard powers, for TPk is also the case in general. However, if A is TP![]() , then
, then ![]() is TP
is TP![]() for all
for all ![]() (see Section 4 in this chapter).
(see Section 4 in this chapter).
The following example resolves the question of those dimensions in which there is Hadamard power closure. Let

Then A is TP but ![]() . Some classes of matrices, such as positive semidefinite matrices, are closed under Hadamard multiplication (see [HJ85, p. 458]), but this class does not form a semigroup. Of course, the opposite situation occurs for TN matrices.
. Some classes of matrices, such as positive semidefinite matrices, are closed under Hadamard multiplication (see [HJ85, p. 458]), but this class does not form a semigroup. Of course, the opposite situation occurs for TN matrices.
The remainder of this chapter is devoted to a number of concepts connected with Hadamard products and Hadamard powers of TPk matrices. We treat Hadamard products first, and then consider the interesting situation of Hadamard powers.
8.1 CONDITIONS UNDER WHICH THE HADAMARD PRODUCT IS TP/TN
The well-known fact that TP matrices are not closed under Hadamard multiplication has certainly not deterred researchers from this interesting topic. In fact, it can be argued that this has fueled considerable investigations on when such closure issues, with particular attention being paid to specific subclasses of TP/TN matrices.
One such instance is the case when both A and B are tridiagonal and TN. This was first proved in [Mar70B]. For completeness, we will carefully write out a proof following this original idea. Then we will outline a second proof which makes use of diagonal scaling.
Proposition 8.1.1 Suppose ![]() and
and ![]() are both n-by-n tridiagonal and IrTN. Then
are both n-by-n tridiagonal and IrTN. Then ![]() is also IrTN and tridiagonal.
is also IrTN and tridiagonal.
Proof. Since it is known that TN2 matrices are closed under Hadamard product, the result holds for n=2. Assume, by induction, that the statement is valid for all such matrices of order at most n-1. To verify the claim, it is sufficient to show that ![]() . The nonnegativity of all other minors of
. The nonnegativity of all other minors of ![]() is implied by induction and the fact that any principal minor is a product of contiguous principal minors. From here the nonnegativity of all the principal minors is sufficient to deduce that a tridiagonal matrix is TN.
is implied by induction and the fact that any principal minor is a product of contiguous principal minors. From here the nonnegativity of all the principal minors is sufficient to deduce that a tridiagonal matrix is TN.
To this end, observe that

Upon a closer examination, it is clear that

can be rewritten as

where ![]() , since
, since ![]() . Thus it follows that E, as defined above, is TN. So by induction,
. Thus it follows that E, as defined above, is TN. So by induction, ![]() , which implies that
, which implies that ![]() .
.
The proof presented above basically follows the ideas as they were laid out in [Mar70B].
We note that Proposition 7.1.1 also follows from the well-known result that positive semidefinite matrices are closed under Hadamard multiplication (see, for example, [HJ85]). If A and B are tridiagonal and IrTN, then there exist positive diagonal matrices DA and DB such that both ![]() and
and ![]() are positive semidefinite. Hence
are positive semidefinite. Hence ![]() is also positive semidefinite, from which we may apply Lemma 0.1.1. and conclude that
is also positive semidefinite, from which we may apply Lemma 0.1.1. and conclude that ![]() is IrTN.
is IrTN.
As noted in Chapter 0, Gantmacher and Krein verified that a generalized Vandermonde matrix, ![]() , where
, where ![]() and
and ![]() is TP. Thus it is evident that if V1 and V2 are two generalized Vandermonde TP matrices (of the same size), then so is
is TP. Thus it is evident that if V1 and V2 are two generalized Vandermonde TP matrices (of the same size), then so is ![]() .
.
Another important example along these lines is the Hadamard product of two TN Routh-Hurwitz matrices (recall Example 0.1.7). It was proved in [GW96]) that the Hadamard product of two TN Routh-Hurwitz matrices is in turn a totally nonnegative matrix. We note that in [Asn70] it was first verified that a polynomial is stable if and only if the associated Routh-Hurwitz matrix is TN. So combining this with the former fact, we may deduce an important result on the entrywise product of two stable polynomials.
There are other examples of subclasses of TN matrices that enjoy closure under Hadamard multiplication, including Green’s matrices [GK02, p. 91]; finite moment matrices of probability measures that are either symmetric about the origin or possesses support on the nonnegative real line (see [Hei94]). As a final example, it was verified in [Wag92] that triangular TN infinite Toeplitz matrices are closed under Hadamard multiplication, but this is definitely not true in the finite case (see the 5-by-5 example presented in [GW96B]).
8.2 THE HADAMARD CORE
Under Hadamard multiplication, it is clear that the all ones matrix, J, plays the role of the identity. Thus there is a TN matrix, namely J, with the property that the Hadamard product of J with any other TN (TP) matrix remains TN (TP). Building on this, it is natural to ask for a description of all TP/TN matrices with the property that the Hadamard product with any TN matrix is again TN. Before we venture too far, observe that if A is an m-by-n matrix that satisfies ![]() is TN for every m-by-n TN matrix B, then certainly A must also be TN, as
is TN for every m-by-n TN matrix B, then certainly A must also be TN, as ![]() will have to be TN.
will have to be TN.
Thus we define the Hadamard core of the m-by-n TN matrices as follows:
![]()
(Note that we drop the dependence on m and n, as the dimensions will be clear from the context.)
Often we may just refer to the Hadamard core to mean the Hadamard core for TN matrices. We now present various elementary properties for matrices in the Hadamard core (the reader is urged to consult [CFJ01], where the Hadamard core originated).
From the discussion above, it is clear that TN![]() is nonempty and that TN
is nonempty and that TN![]() TN. Furthermore, since TN
TN. Furthermore, since TN![]() matrices are closed under Hadamard multiplication, it follows that TN
matrices are closed under Hadamard multiplication, it follows that TN![]() TN whenever
TN whenever ![]() . However, for
. However, for ![]() , TN
, TN![]() is strictly contained in TN (e.g., the matrix W in (8.1) is not in TN
is strictly contained in TN (e.g., the matrix W in (8.1) is not in TN![]() ). Hence TN
). Hence TN![]() becomes an interesting subclass of the m-by-n TN matrices with
becomes an interesting subclass of the m-by-n TN matrices with ![]() .
.
We begin our analysis on the Hadamard core by describing some general properties of matrices in this core and about the subclass TN![]() (see [CFJ01] for the original definition of the Hadamard core and related properties).
(see [CFJ01] for the original definition of the Hadamard core and related properties).
The first property demonstrates that the Hadamard core is closed under Hadamard multiplication–a natural and fundamental property.
Proposition 8.2.1 Suppose A and B are two m-by-n matrices in the Hadamard core. Then ![]() , the Hadamard product of A and B, is in the Hadamard core.
, the Hadamard product of A and B, is in the Hadamard core.
Proof. Let C be any m-by-n TN matrix. Then ![]() is TN since B is in the Hadamard core. Hence
is TN since B is in the Hadamard core. Hence ![]() is TN. But
is TN. But ![]() . Thus
. Thus ![]() is in the Hadamard core, since C was arbitrary.
is in the Hadamard core, since C was arbitrary.
The next basic fact mirrors the inheritance property enjoyed by submatrices of TN matrices.
Proposition 8.2.2 An m-by-n TN matrix A is in the Hadamard core if and only if every submatrix of A is in the corresponding Hadamard core.
Proof. The sufficiency is trivial since A is a submatrix of itself. To prove necessity, suppose there exists a submatrix, say ![]() , that is not in the Hadamard core. Then there exists a TN matrix B such that
, that is not in the Hadamard core. Then there exists a TN matrix B such that ![]() is not TN. Embed B into an m-by-n TN matrix
is not TN. Embed B into an m-by-n TN matrix ![]() such that
such that ![]() , and
, and ![]() otherwise. Since
otherwise. Since ![]() is a submatrix of
is a submatrix of ![]() and
and ![]() is not TN, we have that
is not TN, we have that ![]() is not TN.
is not TN.
The next interesting property follows directly from the multilinearity of the determinant and is concerned with the collection of columns that can be inserted into a matrix so as to preserve the property of being in the Hadamard core ([CFJ01]). We say that a column m-vector v is inserted in column k (![]() ) of an m-by-n matrix
) of an m-by-n matrix ![]() , with columns
, with columns ![]() , if we obtain the new m-by-(n+1) matrix of the form
, if we obtain the new m-by-(n+1) matrix of the form ![]() .
.
Proposition 8.2.3 The set of columns (or rows) that can be appended to an m-by-n TN matrix in the Hadamard core so that the resulting matrix remains in the Hadamard core is a nonempty convex set.
Proof. Suppose A is an m-by-n TN matrix in the Hadamard core. Let S denote the set of columns that can be appended to A so that the new matrix remains in the Hadamard core. Since ![]() , we have that
, we have that ![]() . Let
. Let ![]() . Then the augmented matrices
. Then the augmented matrices ![]() and
and ![]() are both in the Hadamard core. Suppose
are both in the Hadamard core. Suppose ![]() and consider the matrix
and consider the matrix ![]() . Let
. Let ![]() be any m-by-(n+1) TN matrix. Then
be any m-by-(n+1) TN matrix. Then
![]()
We only consider submatrices of ![]() that involve column n+1. Let
that involve column n+1. Let ![]() denote any such square submatrix of
denote any such square submatrix of ![]() . Then
. Then

as ![]() and
and ![]() are both in the Hadamard core. This completes the proof.
are both in the Hadamard core. This completes the proof.
Since any entrywise nonnegative rank one matrix is diagonally equivalent to J, it is not difficult to deduce that any rank one TN matrix is in the Hadamard core. In fact, the core itself is clearly closed under diagonal equivalence in general.
Proposition 8.2.4 Suppose A is an m-by-n TN matrix in the Hadamard core. Then DAE is in the Hadamard core for any ![]() . In particular, any rank one TN matrix is in the Hadamard core.
. In particular, any rank one TN matrix is in the Hadamard core.
Proof. Suppose A is in TN![]() and that
and that ![]() . Then for any TN matrix B, we have
. Then for any TN matrix B, we have
![]()
as ![]() is TN.
is TN.
To verify the second statement, observe that if A is a rank one TN matrix, then it is easy to show that A=DJE, where ![]() . Since J is always a member of the Hadamard core, we have that DJE is in the Hadamard core. Thus A is in the Hadamard core.
. Since J is always a member of the Hadamard core, we have that DJE is in the Hadamard core. Thus A is in the Hadamard core.
Note that W in (8.1) implies that not all rank two TN matrices are in the Hadamard core, and in fact by directly summing the matrix W with an identity matrix it follows that there exist TN matrices of all ranks greater than one that are not in the Hadamard core.
In Section 8.1 we showed that the Hadamard product of any two tridiagonal TN matrices is again a TN matrix. In fact, we can extend this to conclude that all tridiagonal TN matrices are in TN![]() ([CFJ01]).
([CFJ01]).
Theorem 8.2.5 Let T be an n-by-n TN tridiagonal matrix. Then T is in the Hadamard core.
Proof. The proof is by induction on n; the base case (n=2) follows as TN![]() matrices are closed under the Hadamard product. Suppose the result holds for all such tridiagonal matrices of order less than n. Let B be an arbitrary tridiagonal TN matrix and let A be a TN matrix. Without loss of generality, we may assume that both A and B are IrTN, as the reducible case follows from the irreducible one. As in the proof of Proposition 7.1.1, it is sufficient to prove that
matrices are closed under the Hadamard product. Suppose the result holds for all such tridiagonal matrices of order less than n. Let B be an arbitrary tridiagonal TN matrix and let A be a TN matrix. Without loss of generality, we may assume that both A and B are IrTN, as the reducible case follows from the irreducible one. As in the proof of Proposition 7.1.1, it is sufficient to prove that ![]() . In this case, the proof is essentially the same as in Proposition 8.1.1, since
. In this case, the proof is essentially the same as in Proposition 8.1.1, since

By induction, the latter determinant is nonnegative.
We note here that the proof presented in [CFJ01] (the original reference) made use of the fact that tridiagonal TN matrices are signature similar to M-matrices, which in turn are diagonally similar to diagonally dominant matrices.
We obtain a result from [Mar70B] as a special case.
Corollary 8.2.6 The Hadamard product of any two n-by-n tridiagonal TN matrices is again TN.
We now proceed onto a complete description of TN![]() for
for ![]() , which differs significantly from the case m=2. As we have seen, not all 3-by-3 TN matrices are in TN
, which differs significantly from the case m=2. As we have seen, not all 3-by-3 TN matrices are in TN![]() ; recall that
; recall that

is not a member of TN![]() . In the sequel, W plays a key role in describing TN
. In the sequel, W plays a key role in describing TN![]() .
.
Since TN![]() matrices are closed under Hadamard multiplication, it is not surprising that describing 3-by-3 TN matrices in TN
matrices are closed under Hadamard multiplication, it is not surprising that describing 3-by-3 TN matrices in TN![]() with at least one zero entry is not that complicated. For example, if
with at least one zero entry is not that complicated. For example, if ![]() is TN and 3-by-3, with
is TN and 3-by-3, with ![]() for some pair i,j with
for some pair i,j with ![]() , then A is reducible, and hence A is necessarily in TN
, then A is reducible, and hence A is necessarily in TN![]() . The next result provides some key insight into the potential necessary and sufficient conditions for general membership in TN
. The next result provides some key insight into the potential necessary and sufficient conditions for general membership in TN![]() , and we encourage the reader to consult [CFJ01].
, and we encourage the reader to consult [CFJ01].
Lemma 8.2.7 Let ![]() be a 3-by-3 TN matrix with
be a 3-by-3 TN matrix with ![]() (or
(or ![]() ). Then A is in TN
). Then A is in TN![]() if and only if
if and only if ![]() and
and ![]() are both TN.
are both TN.
Proof. Necessity is obvious as both W and its transpose are TN. For sufficiency assume that both ![]() and
and ![]() are TN. Since
are TN. Since ![]() , it is clear that
, it is clear that ![]() , so the only real assumption being made here is that
, so the only real assumption being made here is that ![]() is TN. Observe that
is TN. Observe that ![]() is a tridiagonal TN matrix. Thus, by Theorem 8.2.5, for any 3-by-3 TN matrix B, we have
is a tridiagonal TN matrix. Thus, by Theorem 8.2.5, for any 3-by-3 TN matrix B, we have ![]() . Moreover, since the (3,1) entry enters positively into the determinant (keeping in mind that all 2-by-2 minors in question are nonnegative), it follows that
. Moreover, since the (3,1) entry enters positively into the determinant (keeping in mind that all 2-by-2 minors in question are nonnegative), it follows that
![]()
which completes the proof.
Toward a characterization of the Hadamard core for 3-by-3 TN matrices, we turn our focus to the SEB factorization of TN matrices. The only minor of concern at this stage is the determinant, as all 2-by-2 minors will nonnegative. So it is natural to ask, how negative can ![]() be for arbitrary 3-by-3 TN matrices?
be for arbitrary 3-by-3 TN matrices?
Assume A, B are two arbitrary 3-by-3 InTN matrices with SEB factorizations
![]()
and
![]()
for given nonnegative numbers ![]() . Thus, we are assuming, by diagonal scaling, that
. Thus, we are assuming, by diagonal scaling, that ![]() . It is a computation to verify that
. It is a computation to verify that

Therefore, if A is a 3-by-3 InTN matrix that satisfies ![]() , then certainly
, then certainly ![]() , for every InTN matrix B. Thus, by continuity we have
, for every InTN matrix B. Thus, by continuity we have ![]() , for all TN matrices B, and so A is in TN
, for all TN matrices B, and so A is in TN![]() . The key issue now is to better understand the conditions
. The key issue now is to better understand the conditions ![]() . Observe that for the matrix A given above, we have
. Observe that for the matrix A given above, we have
![]()
and
![]()
Thus the required conditions are equivalent to
![]()
As a consequence of the above arguments, we have established the following characterization of TN![]() (see [CFJ01]).
(see [CFJ01]).
Theorem 8.2.8 Let A be a 3-by-3 InTN matrix. Then A is in the Hadamard core if and only if ![]() and
and ![]() are both TN, where
are both TN, where

The singular case will follow in a similar manner. However, since ![]() , the assumptions
, the assumptions ![]() and
and ![]() , impose some very restrictive constraints on the entries of A (see [CFJ01] for more details).
, impose some very restrictive constraints on the entries of A (see [CFJ01] for more details).
As a consequence of the above arguments, we have a complete characterization of the 3-by-3 TN matrices that belong to TN![]() .
.
Corollary 8.2.9 Let A be a 3-by-3 TN matrix. Then A is in the Hadamard core if and only if ![]() and
and ![]() are both TN.
are both TN.
We take a moment to observe that if ![]() TN
TN![]() and 3-by-3, then the following determinantal inequality holds,
and 3-by-3, then the following determinantal inequality holds,
![]()
for any 3-by-3 TN matrix B. In the case A is singular, there is nothing to prove, but if both A and B are InTN, then from (8.2) we infer that
![]()
We will revisit this inequality in the next section on Oppenheim’s inequality.
We now present some useful facts and consequences of Corollary 8.2.9, which may also be found in [CFJ01].
Corollary 8.2.10 Let ![]() be a 3-by-3 TN matrix. Then A is in the Hadamard core if and only if
be a 3-by-3 TN matrix. Then A is in the Hadamard core if and only if
![]()
The next example, which originally appeared in [CFJ01], illustrates the conditions above regarding membership in TN![]() .
.
Example 8.2.11 (Pólya matrix) Let ![]() . Define the n-by-n Polya matrix Q whose (i,j)th entry is equal to
. Define the n-by-n Polya matrix Q whose (i,j)th entry is equal to ![]() . Then it is well known (see [Whi52]) that Q is TP for all n. (In fact, Q is diagonally equivalent to a TP Vandermonde matrix.) Suppose Q represents the 3-by-3 Pólya matrix. By Corollary 8.2.10 and the fact that Q is symmetric, Q is in TN
. Then it is well known (see [Whi52]) that Q is TP for all n. (In fact, Q is diagonally equivalent to a TP Vandermonde matrix.) Suppose Q represents the 3-by-3 Pólya matrix. By Corollary 8.2.10 and the fact that Q is symmetric, Q is in TN![]() if and only if
if and only if ![]() , which is equivalent to
, which is equivalent to ![]() . This inequality holds if and only if
. This inequality holds if and only if ![]() . Thus q must satisfy
. Thus q must satisfy ![]() . It is easy to check that the inequality holds for
. It is easy to check that the inequality holds for ![]() , where
, where ![]() (the golden mean). Hence Q is in TN
(the golden mean). Hence Q is in TN![]() for all
for all ![]() .
.
Corollary 8.2.12 Let ![]() be a 3-by-3 TN matrix. Suppose
be a 3-by-3 TN matrix. Suppose ![]() is the unsigned classical adjoint matrix of A. Then A is in the Hadamard core if and only if
is the unsigned classical adjoint matrix of A. Then A is in the Hadamard core if and only if ![]() , and
, and ![]() ; or, equivalently,
; or, equivalently,
![]()
and
![]()
Even though Corollary 8.2.12 is simply a recapitulation of Corollary 8.2.10, the conditions rewritten in the above form aid in the proof of the next fact. Recall that if A is a nonsingular TN matrix, then ![]() is a TN matrix in which
is a TN matrix in which ![]() (see, e.g., [GK02, p. 109] or Section 1.3).
(see, e.g., [GK02, p. 109] or Section 1.3).
Theorem 8.2.13 Suppose A is a 3-by-3 nonsingular TN matrix in the Hadamard core. Then ![]() is in the Hadamard core.
is in the Hadamard core.
Proof. Observe that ![]() is TN and, furthermore
is TN and, furthermore ![]() , where
, where ![]() is the unsigned classical adjoint of A. Hence
is the unsigned classical adjoint of A. Hence ![]() is in TN
is in TN![]() if and only if B is a member of TN
if and only if B is a member of TN![]() . Observe that the inequalities in Corollary 8.2.12 are symmetric in the corresponding entries of A and B. Thus B is in TN
. Observe that the inequalities in Corollary 8.2.12 are symmetric in the corresponding entries of A and B. Thus B is in TN![]() . This completes the proof.
. This completes the proof.
Corollary 8.2.14 Let A be a 3-by-3 TN matrix whose inverse is tridiagonal. Then A is in the Hadamard core.
In [GK60] it was shown that the set of all inverse tridiagonal TN matrices is closed under Hadamard multiplication. (In the symmetric case, which can be assumed without loss of generality, an inverse tridiagonal matrix is often called a Green’s matrix, as was the case in [GK60] and [GW96B], and see Chapter 0.) The above result strengthens this fact in the 3-by-3 case. However, it is not true in general that inverse tridiagonal TN matrices are contained in TN![]() . For
. For ![]() , TN
, TN![]() does not enjoy the “inverse closure” property as in Theorem 8.2.13. Consider the following example from [CFJ01].
does not enjoy the “inverse closure” property as in Theorem 8.2.13. Consider the following example from [CFJ01].
Example 8.2.15 Let  where
where ![]() are chosen so that A is positive definite. Then it is easy to check that A is TN, and the inverse of A is tridiagonal. Consider the upper right 3-by-3 submatrix of A, namely
are chosen so that A is positive definite. Then it is easy to check that A is TN, and the inverse of A is tridiagonal. Consider the upper right 3-by-3 submatrix of A, namely 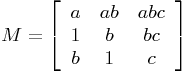 , which is TN. By Proposition 8.2.2, if A is in TN
, which is TN. By Proposition 8.2.2, if A is in TN![]() , then M is in TN
, then M is in TN![]() . However,
. However, ![]() , since
, since ![]() . Thus A is not in TN
. Thus A is not in TN![]() .
.
We can extend this analysis to the rectangular 3-by-n case in the following manner. For ![]() let
let ![]() be the 3-by-n TN matrix consisting of entries
be the 3-by-n TN matrix consisting of entries

For ![]() let
let ![]() be the 3-by-n TN matrix consisting of entries
be the 3-by-n TN matrix consisting of entries

For example, if n=5 and k=3, then

and

See the work [CFJ01] for an original reference.
Theorem 8.2.16 Let A be a 3-by-n (![]() ) TN matrix. Then A is in the Hadamard core if and only if
) TN matrix. Then A is in the Hadamard core if and only if ![]() is TN for
is TN for ![]() and
and ![]() is TN for
is TN for ![]() .
.
Proof. The necessity is obvious, since ![]() and U(j) are both TN. Observe that it is enough to show that every 3-by-3 submatrix of A is in TN
and U(j) are both TN. Observe that it is enough to show that every 3-by-3 submatrix of A is in TN![]() by Proposition 8.2.2. Let B be any 3-by-3 submatrix of A. Consider the matrices
by Proposition 8.2.2. Let B be any 3-by-3 submatrix of A. Consider the matrices ![]() and
and ![]() for
for ![]() and
and ![]() . By hypothesis
. By hypothesis ![]() and
and ![]() are TN. Hence by considering appropriate submatrices it follows that
are TN. Hence by considering appropriate submatrices it follows that ![]() and
and ![]() are both TN. Therefore B is in TN
are both TN. Therefore B is in TN![]() by Corollary 8.2.9. Thus A is in TN
by Corollary 8.2.9. Thus A is in TN![]() .
.
Of course by transposition, we may obtain a similar characterization of TN![]() in the n-by-3 case.
in the n-by-3 case.
At present no characterization of the Hadamard core for 4-by-4 TN matrices is known. A potential reason for the complications that arise in the 4-by-4 case is that all known proofs regarding membership in TN![]() for 3-by-3 TN matrices are rather computational in nature. We expect there is more to learn about TN
for 3-by-3 TN matrices are rather computational in nature. We expect there is more to learn about TN![]() in the 3-by-3 case.
in the 3-by-3 case.
In any event the question is is there a finite collection of (test) matrices that are needed to determine membership in TN![]() ? If so, must they have some special structure? For example, in the 3-by-3 case all the entries of the test matrices are either zero or one.
? If so, must they have some special structure? For example, in the 3-by-3 case all the entries of the test matrices are either zero or one.
8.3 OPPENHEIM’S INEQUALITY
As mentioned in the previous sections, the Hadamard product plays a substantial role within matrix analysis and in its applications (see, for example, [HJ91, chap. 5]).
Some classes of matrices, such as the positive semidefinite matrices, are closed under Hadamard multiplication, and with such closure, investigations into inequalities involving the Hadamard product, usual product, determinants, eigenvalues, are interesting to consider. For example, Oppenheim’s inequality states that
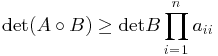
for any two n-by-n positive semidefinite matrices A and B (see [HJ85, p. 480]). Combining Oppenheim’s inequality with Hadamard’s determinantal inequality (![]() ) gives
) gives
![]()
Hence the Hadamard product dominates the conventional product in determinant throughout the class of positive semidefinite matrices.
For the case in which A and B are TN, it is certainly not true in general that ![]() , so there is no hope that Oppenheim’s inequality holds for arbitrary TN matrices. However, in [Mar70B] it was shown that Oppenheim’s inequality holds for the special class of tridiagonal TN matrices. This suggests that an Oppenheim type inequality may be valid in the context of the Hadamard core.
, so there is no hope that Oppenheim’s inequality holds for arbitrary TN matrices. However, in [Mar70B] it was shown that Oppenheim’s inequality holds for the special class of tridiagonal TN matrices. This suggests that an Oppenheim type inequality may be valid in the context of the Hadamard core.
Indeed this is the case, as we see in the next result ([CFJ01]), which generalizes Markham’s inequality for the case of tridiagonal TN matrices.
Theorem 8.3.1 Let A be an n-by-n TN matrix in the Hadamard core, and suppose B is any n-by-n TN matrix. Then

Proof. If B is singular, then there is nothing to show, since ![]() , as A is in the Hadamard core. Assume B is nonsingular. If n=1, then the inequality is trivial. Suppose, by induction, that Oppenheim’s inequality holds for all (n-1)-by-(n-1) TN matrices A and B with A in the Hadamard core. Suppose A and B are n-by-n TN matrices and assume that A is in the Hadamard core. Let A11 (B11) denote the principal submatrix obtained from A (B) by deleting row and column 1. Then by induction
, as A is in the Hadamard core. Assume B is nonsingular. If n=1, then the inequality is trivial. Suppose, by induction, that Oppenheim’s inequality holds for all (n-1)-by-(n-1) TN matrices A and B with A in the Hadamard core. Suppose A and B are n-by-n TN matrices and assume that A is in the Hadamard core. Let A11 (B11) denote the principal submatrix obtained from A (B) by deleting row and column 1. Then by induction

Since B is nonsingular, by Fischer’s inequality B11 is nonsingular. Consider the matrix ![]() , where
, where ![]() and E11 is the (1,1) standard basis matrix. Then
and E11 is the (1,1) standard basis matrix. Then ![]() , and
, and ![]() is TN (see Lemma 9.5.2). Therefore
is TN (see Lemma 9.5.2). Therefore ![]() is TN and
is TN and ![]() . Observe that
. Observe that ![]() Thus
Thus

as desired.
As in the positive semidefinite case, as any TN matrix also satisfies Hadamard’s determinantal inequality, we have
Corollary 8.3.2 Let A be an n-by-n TN matrix in the Hadamard core, and suppose B is any n-by-n TN matrix. Then
![]()
We close this section with some further remarks about Oppenheim’s inequality. In the case in which ![]() and
and ![]() are n-by-n positive semidefinite matrices, it is clear from Oppenheim’s inequality that
are n-by-n positive semidefinite matrices, it is clear from Oppenheim’s inequality that

However, in the case in which A is in the Hadamard core and B is an n-by-n TN matrix, it is not true in general that ![]() . Consider the following example ([CFJ01]).
. Consider the following example ([CFJ01]).
Example 8.3.3 Let A be any 3-by-3 TP matrix in TN![]() , and let B=W, the 3-by-3 TN matrix equal to
, and let B=W, the 3-by-3 TN matrix equal to  . Then since the (1,3) entry of A enters positively into
. Then since the (1,3) entry of A enters positively into ![]() it follows that
it follows that
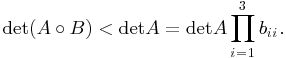
If, however, both A and B are in TN![]() , then we have the next result, which is a direct consequence of Theorem 8.3.1.
, then we have the next result, which is a direct consequence of Theorem 8.3.1.
Corollary 8.3.4 Let ![]() and
and ![]() be two n-by-n matrices in TN
be two n-by-n matrices in TN![]() . Then
. Then

The next example sheds some light on the necessity that A be in TN![]() in order for Oppenheim’s inequality to hold. In particular, we show that if A and B are TN and
in order for Oppenheim’s inequality to hold. In particular, we show that if A and B are TN and ![]() is TN, then Oppenheim’s inequality need not hold ([CFJ01]).
is TN, then Oppenheim’s inequality need not hold ([CFJ01]).
Example 8.3.5 Let  and
and ![]() . Then A (and hence B) is TN, and
. Then A (and hence B) is TN, and ![]() . Now
. Now

and it is not difficult to verify that ![]() is TN with
is TN with ![]() . However, in this case
. However, in this case

8.4 HADAMARD POWERS OF TP2
If ![]() is an entrywise nonnegative m-by-n matrix, then for any
is an entrywise nonnegative m-by-n matrix, then for any ![]() ,
,
![]()
denotes the tth Hadamard power of A. It is easily checked that if A is TN![]() (TP
(TP![]() ), then
), then ![]() is TN
is TN![]() (TP
(TP![]() ).
).
In previous sections we observed that TN![]() and TP
and TP![]() are not in general closed under Hadamard multiplication; however, it is the case that if A is TN
are not in general closed under Hadamard multiplication; however, it is the case that if A is TN![]() , then
, then ![]() is TN
is TN![]() for all
for all ![]() . For completeness’ sake, we use an example to indicate the need for the power t to be at least one in the above claim. Let
. For completeness’ sake, we use an example to indicate the need for the power t to be at least one in the above claim. Let

Then A is TN, but ![]() , for all t with
, for all t with ![]() . To verify the claim above that
. To verify the claim above that ![]() is TN
is TN![]() for all
for all ![]() , we analyze the function
, we analyze the function ![]() , for
, for ![]() , which turns out to be an exponential polynomial in the entries of the 3-by-3 TP matrix A, assuming A is of the form:
, which turns out to be an exponential polynomial in the entries of the 3-by-3 TP matrix A, assuming A is of the form:

where ![]() . It then follows that
. It then follows that ![]() is an exponential polynomial, and when the terms in the determinant expansion are ordered in descending order in terms of the bases
is an exponential polynomial, and when the terms in the determinant expansion are ordered in descending order in terms of the bases ![]() , there are three changes in sign. From this it follows that such a polynomial will have at most three nonnegative roots. The remainder of the proof, which is only sketched here, requires that
, there are three changes in sign. From this it follows that such a polynomial will have at most three nonnegative roots. The remainder of the proof, which is only sketched here, requires that ![]() be TP whenever A is TP. This follows from an easy application of Sylvester’s determinantal formula (see Section 1.2).
be TP whenever A is TP. This follows from an easy application of Sylvester’s determinantal formula (see Section 1.2).
Let  be TP. Then, using Sylvester’s expansion for the determinant, we have that
be TP. Then, using Sylvester’s expansion for the determinant, we have that
![]()
Since A is TP, the following inequalities hold:
(1) ![]()
(2) ![]()
(3) ![]() .
.
These inequalities and det A > 0 are then used to establish that ![]() is TP.
is TP.
Returning to Hadamard powers for larger order matrices, we may observe by example that TN (TP) matrices are not, in general, Hadamard power closed.
Example 8.4.1 Let

Then A is TP but ![]() . Thus
. Thus ![]() is not TP.
is not TP.
Hadamard powers of TN matrices have been considered by others, motivated in part by applications. One of the most noteworthy works (in the context of TN matrices) is [GT98], where it was shown that all Hadamard powers (at least one) of a TN Routh-Hurwitz matrix (see Example 0.1.7) remain TN.
Recall as well from Section 8.2, that if A is in TN![]() , then
, then ![]() is in TN
is in TN![]() for all positive integers p.
for all positive integers p.
We now consider continuous Hadamard powers of TP![]() matrices and show that eventually such powers become TP (see [FJ07b] for more work along these lines). We say that an entrywise nonnegative matrix A is eventually TN (TP), or is eventually of positive determinant (assuming that A is square), if there exists a
matrices and show that eventually such powers become TP (see [FJ07b] for more work along these lines). We say that an entrywise nonnegative matrix A is eventually TN (TP), or is eventually of positive determinant (assuming that A is square), if there exists a ![]() such that
such that ![]() is TN (TP) or has a positive determinant for all
is TN (TP) or has a positive determinant for all ![]() . We also say that a nonnegative matrix A eternally has a given property if
. We also say that a nonnegative matrix A eternally has a given property if ![]() has the desired property for all
has the desired property for all ![]() .
.
It is clear that if A is an n-by-n matrix that is diagonally equivalent (via positive diagonal matrices) to a matrix that is eventually of positive determinant, then A must be eventually of positive determinant.
We call an n-by-n nonnegative matrix ![]() normalized dominant if
normalized dominant if ![]() ,
, ![]() and
and ![]() , for
, for ![]() .
.
Lemma 8.4.2 If A is an n-by-n normalized dominant matrix, then A is eventually of positive determinant.
The crux of the argument relies on the fact that since the off-diagonal entries of ![]() tend to zero as t increases, it is then clear that
tend to zero as t increases, it is then clear that ![]() will approach one as t increases.
will approach one as t increases.
To better understand the matrices that are eventually of positive determinant, we let TN![]() denote the subset of TN
denote the subset of TN![]() in which all contiguous 2-by-2 principal minors are positive. Observe that if A is in TN
in which all contiguous 2-by-2 principal minors are positive. Observe that if A is in TN![]() , then A is reducible if and only if at least one entry of the form
, then A is reducible if and only if at least one entry of the form ![]() or
or ![]() is zero. The next result first appeared in [FJ07b], which we include with a proof for completeness.
is zero. The next result first appeared in [FJ07b], which we include with a proof for completeness.
Lemma 8.4.3 If A is n-by-n and ![]() +2
+2 ![]() , then A is diagonally equivalent (via positive diagonal matrices) to a normalized dominant matrix.
, then A is diagonally equivalent (via positive diagonal matrices) to a normalized dominant matrix.
Proof. Suppose ![]() +2
+2 ![]() and assume that A is irreducible. Then, the diagonal, and the super- and subdiagonal entries of A must all be positive. Hence there exist positive diagonal matrices
and assume that A is irreducible. Then, the diagonal, and the super- and subdiagonal entries of A must all be positive. Hence there exist positive diagonal matrices ![]() such that B=DAE, and such that B has ones on its main diagonal. Furthermore, we can find a positive diagonal matrix F such that
such that B=DAE, and such that B has ones on its main diagonal. Furthermore, we can find a positive diagonal matrix F such that ![]() has ones on its main diagonal and has symmetric tridiagonal part (i.e.,
has ones on its main diagonal and has symmetric tridiagonal part (i.e., ![]() , for each
, for each ![]() ). Since C is in TNP2+ and is normalized, it follows that
). Since C is in TNP2+ and is normalized, it follows that ![]() , for each
, for each ![]() . We establish that each of the off-diagonal entries are strictly less than one by sequentially moving along each diagonal of the form
. We establish that each of the off-diagonal entries are strictly less than one by sequentially moving along each diagonal of the form ![]() for
for ![]() . Let
. Let ![]() ; to demonstrate that
; to demonstrate that ![]() , consider the 2-by-2 minor of C based on rows
, consider the 2-by-2 minor of C based on rows ![]() and columns
and columns ![]() . Assuming that all the entries of C of the form
. Assuming that all the entries of C of the form ![]() for
for ![]() have been shown to be strictly less than one, it follows that
have been shown to be strictly less than one, it follows that ![]() by using the nonnegativity of the 2-by-2 minor of C based on rows
by using the nonnegativity of the 2-by-2 minor of C based on rows ![]() and columns
and columns ![]() . By induction all the entries above the main diagonal of C are strictly less than one. Similar arguments apply to the entries below the main diagonal. Hence C is a normalized dominant matrix.
. By induction all the entries above the main diagonal of C are strictly less than one. Similar arguments apply to the entries below the main diagonal. Hence C is a normalized dominant matrix.
Suppose ![]() +2
+2 ![]() and A is reducible. We verify this case by induction on n. If n=2, then A is triangular and the conclusion follows easily. Suppose that any
and A is reducible. We verify this case by induction on n. If n=2, then A is triangular and the conclusion follows easily. Suppose that any ![]() +2
+2 ![]() of size less than n is diagonally equivalent to a normalized dominant matrix. Assume that A is an n-by-n TNP2+ matrix and is reducible. Then for some i, with
of size less than n is diagonally equivalent to a normalized dominant matrix. Assume that A is an n-by-n TNP2+ matrix and is reducible. Then for some i, with ![]() , we have
, we have ![]() (if the only zero entry occurs on the subdiagonal consider transposition). Since
(if the only zero entry occurs on the subdiagonal consider transposition). Since ![]() +2
+2 ![]() , all the main diagonal entries of A must be positive, from which it follows that
, all the main diagonal entries of A must be positive, from which it follows that ![]() for all
for all ![]() and
and ![]() . In particular, A must be in the form
. In particular, A must be in the form

where A1 is i-by-i, A3 is ![]() -by-
-by-![]() , and both A1 and A3 are TNP2+. By induction, both A1 and A3 are diagonally equivalent to a normalized dominant matrix. To complete the argument, consider a diagonal similarity of A via a diagonal matrix of the form
, and both A1 and A3 are TNP2+. By induction, both A1 and A3 are diagonally equivalent to a normalized dominant matrix. To complete the argument, consider a diagonal similarity of A via a diagonal matrix of the form  , with
, with ![]() and small.
and small.
A simple consequence of the above results is the following ([FJ07b]).
Corollary 8.4.4 If A is n-by-n and ![]() +2
+2 ![]() , then A is eventually of positive determinant. In particular, if A is n-by-n and
, then A is eventually of positive determinant. In particular, if A is n-by-n and ![]() _2
_2 ![]() , then A is eventually of positive determinant.
, then A is eventually of positive determinant.
We may now offer a characterization of eventually TP matrices under Hadamard powers, which does appear in [FJ07b].
Theorem 8.4.5 Suppose A is an m-by-n matrix. Then the following statements are equivalent:
(1) A is eventually TP;
(2) A is TP2;
(3) A is entrywise positive, and all 2-by-2 contiguous minors of A are positive.
Proof. (1) ⇛ (2): Suppose A is eventually TP. Then clearly A must have positive entries. Since the 2-by-2 minor in rows ![]() and columns
and columns ![]() in
in ![]() is positive for some t, we have
is positive for some t, we have ![]() . By taking tth roots, this minor is positive in A. Since this is true of any 2-by-2 minor,
. By taking tth roots, this minor is positive in A. Since this is true of any 2-by-2 minor, ![]() _2
_2 ![]() .
.
(2) ⇛ (3): Trivial.
(3) ⇛ (1): If (3) holds, then, by Corollary 3.1.6, each submatrix of A is TP2, and so by Corollary 7.5.3, this submatrix is eventually of positive determinant. Hence A is eventually TP.
Corollary 8.4.6 If A is TP, then A is eventually TP.
We observe that some of the work in [KV06] is very much related to eventuality of TP![]() matrices.
matrices.
If we relax the conditions in Theorem 7.5.5 that A be just in TN2, then A need not be eventually TN or TP. Consider the example,

Then A is TN2 and has positive entries, but no Hadamard power of A is TN. This is easily seen since for any Hadamard power the principal minor lying in rows and columns ![]() is always negative. Notice that not all 2-by-2 minors of A based on consecutive indices are positive. Thus we need an additional condition on a matrix A in TN2 to ensure that A is eventually TN, which is determined in what follows.
is always negative. Notice that not all 2-by-2 minors of A based on consecutive indices are positive. Thus we need an additional condition on a matrix A in TN2 to ensure that A is eventually TN, which is determined in what follows.
A matrix in TN2 is called 2-regular if each two consecutive lines (rows or columns) constitute a linearly independent set (see also Section 7.3). Note that a 2-regular TN2 matrix has no zero lines. For the purposes of the next result, we introduce a new term that is a variant of the “shadow” terminology defined in Chapter 7. Suppose that A in TN![]() is 2-regular. Then we say that A satisfies a 2-shadow condition if when the rank
is 2-regular. Then we say that A satisfies a 2-shadow condition if when the rank![]() , then either the submatrix of A of the form
, then either the submatrix of A of the form ![]() or
or ![]() has rank one. In other words, such an A satisfies the 2-shadow property if whenever a 2-by-2 contiguous submatrix B of A is singular, then at least one of the contiguous submatrices of A such that B lies in the northeast corner or the southwest corner (i.e., one of the shadows of
has rank one. In other words, such an A satisfies the 2-shadow property if whenever a 2-by-2 contiguous submatrix B of A is singular, then at least one of the contiguous submatrices of A such that B lies in the northeast corner or the southwest corner (i.e., one of the shadows of ![]() ) has rank one (see also Section 7.2).
) has rank one (see also Section 7.2).
If we let  , then A is in TN
, then A is in TN![]() and is 2-regular, but A does not satisfy the 2-shadow condition.
and is 2-regular, but A does not satisfy the 2-shadow condition.
Suppose A had two consecutive rows (or columns) that were multiples of each other. Then A is eventually TN if and only if the matrix obtained from A by deleting one of these rows is eventually TN. Thus, with regard to assessing eventually TN, there is no loss of generality in assuming that A is 2-regular.
The next result, characterizing the TN![]() matrices that are eventually TN, first appeared in [FJ07b], where details of the proof can be found.
matrices that are eventually TN, first appeared in [FJ07b], where details of the proof can be found.
Theorem 8.4.7 Suppose that A is an m-by-n 2-regular matrix. Then A is eventually TN if and only if ![]() _2
_2 ![]() and A satisfies the 2-shadow condition.
and A satisfies the 2-shadow condition.
We may now also conclude that
Corollary 8.4.8 If A is TN, then A is eventually TN.
