Chapter Ten

Other Related Topics on TN Matrices

10.0 INTRODUCTION AND TOPICS

Part of the motivation for this work grew out of the fact that total positivity and, in particular, TP matrices arise in many parts of mathematics and have a broad history, and, therefore, a summary of this topic seems natural. This is what we have tried to accomplish here. There are many facts and properties about TP and TN matrices that neither fit well in another chapter nor are as lengthy as a separate chapter. Yet, these topics are worthy of being mentioned and discussed. Thus, in some sense this final chapter represents a catalog of additional topics dealing with other aspects of TN matrices. These topics include powers of TP/TN matrices, a generalization of direct summation in conjunction with TN matrices, and TP/TN polynomial matrices.

10.1 POWERS AND ROOTS OF TP/TN MATRICES

It is an important feature of square TN and TP matrices that each class is closed under positive integer (conventional) powers (Cauchy-Binet). Moreover, sufficiently high powers of IITN matrices are necessarily TP (by definition). Indeed, even the InTN and TP matrices are closed under negative integer powers, except for the “checkerboard” signature similarity (see Chapter 1).

In addition to integer powers, continuous real powers of TP matrices and InTN matrices are well defined in a natural way, just as they are for positive definite matrices. If A is InTN and A = UDW with D a positive diagonal matrix (and WU=I), then is uniquely defined for all . This definition also gives continuous dependence on t that agrees with conventional integer powers at all integer values of t. What, then, about A^t when A is TP and t>1 or 0<t<1 (e.g., , for k a positive integer)? If A is n-by-n and n>2, in neither case is A^t necessarily TP. (For , it is a nice exercise that A^t is TP for t>0.) This is not surprising for 0<t<1, though it lies in contrast with the positive definite case, but for t>1, it is not so clear what to expect. Consider the TP matrix

Then A is TP and its unique square root with all positive eigenvalues is (approximately) given by

It is clear, via the negative entries, that B is not TP.

In general, under what circumstances roots are TP, or continuous powers larger than 1 are TP, is not known. Because of the threshold conditions of Theorem 5.3.5, continuous powers will eventually be TP when the eigenvalue ratios become large enough.

Theorem 10.1.1 For each TP (resp. InTN) matrix A, there is a positive number T such that for all t>T, A^t is TP (resp. InTN).

We note the similarity of this result for continuous conventional powers with the result (Corollary 7.5.6) for continuous Hadamard powers. It follows that

Corollary 10.1.2 For each TP (resp. InTN) matrix A there is a positive number T such that for all t>T, A^t and are both TP (resp. InTN).

The subset of TP consisting of those matrices for which the above constant is at most 1 has not yet been fully studied. It is continuous power closed in both senses.

We close this section by mentioning a couple of related results on this topic. As we discussed above, the class IITN is not closed under extraction of square roots, or any other roots for that matter. We may deduce this in another interesting fashion by choosing a tridiagonal example. Suppose A is IITN and tridiagonal, and assume there is a kth root, k>1; call it B. If the matrix B is even in IITN, it must be irreducible, else A would be reducible. Since B would have to be irreducible, its entries on the main diagonal, and sub- and superdiagonals must be positive. It follows that the kth power, , of B will have more positive entries than a tridiagonal matrix. Since A is tridiagonal, this contradicts . We know of no simple characterization of IITN matrices with square roots in IITN.

What about TP matrices? This class rules out the tridiagonal example above. Could it be an (n-1)st power of a tridiagonal matrix in InTN? This, in fact, can never happen, unless the TP matrix, call it A, is symmetrizable via similarity from . This is because the supposed tridiagonal (n-1)st root, call it B, must be irreducible, and any irreducible nonnegative tridiagonal matrix is diagonally similar to a symmetric one. If is such that is symmetric, then would be symmetric. However, even symmetric TP matrices need not have (symmetric) tridiagonal InTN (n-1)st root, and it is not known which do.

10.2 SUBDIRECT SUMS OF TN MATRICES

Let and suppose that

in which . Then we call

the k-subdirect sum of A and B, which we denote by . When the value of k is irrelevant or clear, we may just refer to a subdirect sum, and when k=0, a 0-subdirect sum is a familiar direct sum, and will be abbreviated to ⊕. Of course, the k-subdirect sum of two matrices is generally not commutative. See [FJ99] for more information and background (including references) on subdirect sums of other positivity classes of matrices.

For a given class of matrices Π four natural questions may be asked:

(I) if A and B are in Π, must a 1-subdirect sum C be in Π;

(II) if

is in Π, may C be written as , such that A and B are both in Π, when C₂₂ is 1-by-1; and

(III) and (IV) the corresponding questions with 1 replaced by .

We begin with a simple determinantal identity, that is useful in consideration of 1-subdirect sums. We provide a proof here for completeness (see [FJ99]).

Lemma 10.2.1 Let

in which and b₂₂ are both 1-by-1. Then

(10.1)

Proof. It is routine to verify that if A₁₁ and B₃₃ are both singular, then is necessarily singular; hence (10.1) holds in this special case. Suppose, then, without loss of generality, that A₁₁ is nonsingular. Using Schur complements (see Chapter 1), it follows that

Expanding the latter determinant by the first row gives

In [FJ99] we considered questions (I)–(IV) for various positivity classes: positive (semi-) definite; M-matrices; symmetric M-matrices; P-matrices; P₀-matrices; doubly nonnegative matrices (entrywise nonnegative positive semidefinite matrices); and completely positive matrices (matrices of the form with B entrywise nonnegative). One of the results proved in [FJ99] is the next result, which addresses specifically questions (I) and (II) for each of the above positivity classes.

Theorem 10.2.2 Let Π denote any one of the above positivity classes. Suppose

is an n-by-n matrix with C₁₁ and C₃₃ square, and with c₂₂ 1-by-1. Then C is in Π if and only if C may be written as , in which both A and B are in Π.

For more information on questions (III) and (IV) for these positivity classes, see [FJ99]. We now turn our attention to the class of TN matrices. The next result answers questions (I) and (II) for the class TN.

Theorem 10.2.3 Let

be an n-by-n matrix with C₁₁ and C₃₃ square, and with c₂₂ 1-by-1. Then C is TN if and only if C may be written as , in which both A and B are TN.

Proof. First, suppose both A and B are TN, and let

where a₂₂ and b₂₂ are both 1-by-1. Note that any principal submatrix of either involves the overlapping entry and hence is nonnegative by (10.1), or does not involve the overlapping entry and is nonnegative since it is a direct sum of TN matrices. Let , and let be any square submatrix of C. Let , , , and .

Furthermore, we can assume , and are all nonempty; otherwise it is straightforward to verify that . Suppose . Then either and or, without loss of generality, and . First assume and . Then

If , then is a direct sum of TN matrices, and hence is TN. Otherwise , and without loss of generality, assume (the case follows by symmetry). Therefore the size of the larger zero block is -by-. Furthermore,

hence . Now assume and . Then

If , then . Hence is block triangular and it follows that . Otherwise, . If , then , and if , then is either block triangular or singular. Thus suppose . Again there are two cases to consider. Suppose . Then , and follows from (10.1). Otherwise suppose , and without loss of generality, assume (the case follows by symmetry). The order of the larger zero block is -by-, and

If , then, as before, . So assume , in which case, it follows that is a block triangular matrix with the diagonal blocks being TN, hence .

Conversely, suppose C is TN. Since

are TN, choose and as small as possible so that

are both TN. Assume and . In what follows we are only concerned with square submatrices of and . Let and let Observe that Γ (similarly Λ) is nonempty, since if Γ were empty, then for every , . Then by continuity we may decrease , while remains TN, which contradicts the minimality of . Therefore Γ is nonempty and, similarly, so is Λ.

Suppose for the moment that . Then increase to a₂₂ and increase to b₂₂ so that , and let

By the observation preceding Theorem 10.2.3, A and B are TN, and . Thus, if we can show , then the proof is complete. So suppose . Then one of two possibilities can occur. Either is singular for every , or there exists such that is nonsingular. Suppose that is singular for every . In this case, each such does not depend on , and hence may be decreased without affecting . Also, as previously noted, if and , then may be decreased in this case. However, this contradicts the minimality of . Thus there exists such that is nonsingular. Similar arguments also show that there exists such that is nonsingular. Furthermore, if is decreased, then . Since , decrease to such that . Then

is a submatrix of C. However, , by (10.1). This is a contradiction, hence , which completes the proof.

The class TN is not closed under addition, hence it follows that the answer to question (III) is negative. However, even more goes wrong.

Example 10.2.4

Then A and B are both TN matrices. However,

is not a TN matrix since . Note that the sum in the overlapping positions is a totally nonnegative matrix.

To address question (IV), as in [FJ99], we will make strong use of the fact that TN matrices can be factored into TN matrices L and U (see Chapter 2).

Lemma 10.2.5 Let

in which C₂₂ and C₃₃ are square and C₁₁ is m-by-m (). Suppose C is TN. Then

in which L and U (partitioned conformally with C) are both TN.

We are now in a position to prove an affirmative answer to question (IV) for the class TN ([FJ99]).

Theorem 10.2.6 Let

in which C₁₁ and C₃₃ are square, and with C₂₂ k-by-k. If C is TN, then C can be written as so that A and B are TN.

Proof. By Lemma 10.2.5, C=LU, in which both L and U are TN, and and . Then it is easy to check that

Hence C can be written as

Notice that if

and

then . Each of the four matrices on the right is easily seen to be TN because L and U are, and it follows from the multiplicative closure of the class TN that both A and B are TN, which completes the proof of the theorem.

A final result of interest, which has also been mentioned in the context of tridiagonal matrices in Chapter 0, is that for nonnegative tridiagonal matrices the property of being TN or P₀ are equivalent.

Corollary 10.2.7 Suppose that A is an n-by-n entrywise nonnegative tridiagonal matrix. Then A is TN if and only if A is a P₀-matrix (that is, has nonnegative principal minors).

Proof. Since being TN is a stronger property than being P₀, we need only assume that A is P₀. The proof is by induction on n, with the case n=2 being obvious. Since A is tridiagonal and P₀, it follows that , with both B,C being P₀ and tridiagonal. By induction, both B and C are then TN as well. Hence, by Theorem 10.2.3 is TN.

10.3 TP/TN POLYNOMIAL MATRICES

A matrix function may be viewed as one in which each entry is a function of the same collection of variables. Here, we consider square matrix functions A(t) of a single variable t, in which each entry is a polynomial in t, a so-called polynomial matrix In other words, in which is a polynomial in t, , and the coefficients of all our polynomials will be real.

Under what circumstances should a polynomial matrix be called TP, TN or InTN? The definition here is that A(t) is TP (TN, InTN) if for each , A(t) is TP (TN, InTN). Consider the following example: Let

Then is it easily checked that A(t) is a TP polynomial matrix.

To what extent do TP polynomial matrices have properties that mimic TP matrices (or TN or InTN)? In [JS00] it is shown that TP line insertion (Theorem 8.0.2) is still possible for polynomial matrices, that is, if A(t) is an m-by-n polynomial matrix, a polynomial line may be inserted anywhere to produce an -by-n or m-by-(n+1) TP polynomial matrix . This is trivial when only TN is required of both A(t) and .

We also note here that if A(t) is InTN, then A(t) has an elementary bidiagonal factorization in which each bidiagonal factor is a polynomial matrix (with only one nontrivial polynomial entry) that takes on only nonnegative values and the diagonal factor has polynomial diagonal entries, taking on only positive values.

Theorem 10.3.1 Let A(t) be a polynomial matrix. Then A(t) is an InTN polynomial matrix if and only if A(t) has a bidiagonal factorization in which each bidiagonal factor is a polynomial matrix that takes on only nonnegative values and the diagonal factor has polynomial diagonal entries, taking on only positive values.

In addition, A(t) is a TP polynomial matrix if and only if A(t) has a bidiagonal factorization in which all factors are polynomial matrices taking on only positive values.

10.4 PERRON COMPLEMENTS OF TN MATRICES

Perron complements were conceived in connection with a divide and conquer algorithm for computing the stationary distribution vector for a Markov chain (see [Mey89]). For an n-by-n nonnegative and irreducible matrix A, the Perron complement of in A, is given by

(10.2)

in which , , and denotes the spectral radius of a matrix. Recall that since A is irreducible and nonnegative, , so that the expression on the right hand side of (10.2) is well defined. It is known that for A nonnegative, is nonnegative and (see [Mey89] and also [JX93]).

Recall from Chapter 1 that the Schur complement was defined as:

Thus, it is evident that Perron and Schur complements are similar in definition. In [FN01] Perron complements of TN matrices were studied and a generalized version of a Perron complement was defined and studied in connection with TN matrices.

For any and for any , let the extended Perron complement at t be the matrix

(10.3)

which is also well defined since .

Before we address some results on Perron complements of TN matrices, we state an important result, proved in [And87], on Schur complements of TN matrices and the compound ordering (defined in Chapter 5). A key ingredient needed is Sylvester’s determinantal identity (see Chapter 1),

(10.4)

where , and with .

Then we have,

Lemma 10.4.1 If A is an n-by-n TN matrix, and or , then

where and provided that is invertible.

When is the Perron complement of a TN matrix TN? To address this, we verify a quotient formula for the Perron complement that is reminiscent of Haynsworth’s quotient formula for Schur complements.

Recall from Proposition 1.5.1 that Schur complements of TN matrices are again TN whenever the index set in question is contiguous. For Perron complements, we have an analogous result ([FN01]), which we include here with proof.

Lemma 10.4.2 Let A be an n-by-n irreducible TN matrix, and let or and define . Then for any , the matrix

is TN. In particular, the Perron complement is TN for or .

Proof. Assume . (The arguments for the case are similar.) Let A be partitioned as follows

where B is (n-1)-by-(n-1) and e is a scalar. Then , where . Consider the matrix

Observe that . Thus any minor of is just a minor of a related Schur complement. Using the formula (10.4) we have

where . Observe that

The first inequality follows since the matrix on the left is TN and TN matrices satisfy Fischer’s inequality (see Chapter 6). This completes the proof.

Unfortunately, TN matrices are not closed under arbitrary Perron complementation, even when β is a singleton as the next example demonstrates. Note that the same example appears in [FN01], as such examples are not easy to produce.

Example 10.4.3 Recall from Chapter 0 that a polynomial f(x) is said to be stable if all the zeros of f(x) have nonpositive real parts. Further, if f(x) is a stable polynomial, then the Routh-Hurwitz matrix formed from f is TN.

Consider the polynomial

It can be shown that f is a stable polynomial. Hence its associated Routh–Hurwitz array is TN call it H. Let (which is 9-by-9). Then P is not TN, as , for example.

Recall Haynsworth’s quotient formula (see, for example, [FN01]) which can be stated as follows. For ,

Rather than denote Schur and Perron complements with respect to principal submatrices, we will denote them only by their index sets. For example, if A is n-by-n and , then we denote by and by . Along these lines, we have (as in [FN01])

Theorem 10.4.4 Let A be any n-by-n irreducible nonnegative matrix, and fix any nonempty set . Then for any with and , we have

for any .

Proof. Observe that for any index set , the following identity holds:

Hence we have

The second to last equality follows from the quotient formula for Schur complements. This completes the proof.

Using this quotient formula for extended Perron complements and Lemma 10.4.2, we have the next result ([FN01]).

Theorem 10.4.5 Let A be an n-by-n irreducible TN matrix, and let such that is contiguous. Then for any , the matrix

is TN. In particular, the Perron complement is TN whenever is contiguous.

The next result is a consequence of the previous theorem; its proof can be found in [FN01].

Corollary 10.4.6 Let A be an n-by-n irreducible tridiagonal TN matrix. Then for any , the matrix

where , is irreducible tridiagonal and totally nonnegative.

The next fact involves an ordering between the compounds of extended Perron complements and Schur complements of TN matrices discussed earlier (also referred to as the compound ordering). Recall from Lemma 10.4.1 that if or , then

where and provided that is invertible. In the same spirit we have the following result, as in [FN01], which is included here with proof.

Theorem 10.4.7 Let A be an n-by-n irreducible TN matrix, and let such that is a contiguous set. Then for any ,

Proof. Suppose and . It is enough to verify the inequality , as the remaining two inequalities are contained in Lemma 10.4.1. We begin with . Recall from Lemma 10.4.2 that if

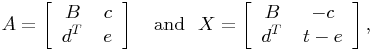
then for any

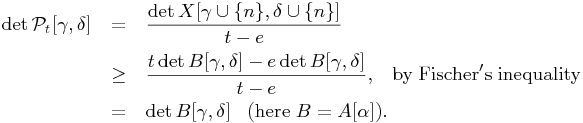
Thus , as desired. We are now ready to proceed with the case when β is not a singleton, namely, , . Let and let . Then K is irreducible and, by Lemma 10.4.2, we also know that K is a TN matrix. But then applying the initial part of the proof to K we see that

The last inequality follows since is inherited by submatrices. The claim of the theorem now follows by repeating this argument as many times as necessary and making use of the quotient formula in Theorem 10.4.4.

Thus far we have shown that if or and , then

(10.5)

More generally, suppose such that is a contiguous set. Then , and hence . Thus, by Theorem 10.4.4,

Applying (10.5) twice we have

as desired. The remaining inequalities, namely , follow from the remarks preceding Theorem 10.4.7. This completes the proof.