Chapter Nine

Extensions and Completions

9.0 LINE INSERTION

The property that a matrix be TP is sufficiently strong that, at first glance, construction seems even more difficult than recognition. Of course, the elementary bidiagonal factorization provides an easy way simply to write down an example, but with this factorization it is very difficult to “design” many entries of the resulting matrix. Here, we review a variety of construction, extension and completion ideas for both TP and TN matrices.

Another way to produce a TP matrix is a technique that follows the simple diagram

This “exterior bordering” technique represents a strategy for extending any existing TP matrix by adding a line (a row) above or below or (a column) to the right or left. Since a positive number is also a TP matrix, the procedure may be begun, easily, with any positive number. To obtain, for example, an (m+1)-by-n TP matrix from an m-by-n one by adding an additional row at the bottom, choose an arbitrary positive entry for the (m+1,1) position. Then choose an entry for the (m+1,2) position that is sufficiently large as to make the lower left 2-by-2 minor positive, then an entry for the (m+1,3) position that makes the lower left 3-by-3 minor positive, and so on until the additional row is completed. Note that, by making the lower left k-by-k minor positive, the lower right (k-1)-by-(k-1) minor of it will necessarily be positive by Sylvester’s determinantal identity (1.5) and other noncontiguous minors that include the new entry will be positive by the sufficiency of the contiguous ones (see Corollary 3.1.5). Thus, to produce the new TP matrix with one more row, all numbers greater than the threshold that makes each k-by-k lower left minor zero will suffice. This gives well-defined and calculable bounds. Addition of a row at the top is similar, but by working right-to-left (instead of left-to-right). Adding a column on the left (resp. right) may be accomplished by working bottom-to-top (resp. top-to-bottom) in a similar way, all as indicated in the diagram above. Note that in each case, one works toward either the northwes or the southeast corner. Extension of a TN matrix to a larger TN one may be accomplished more simply, either by adding zeros or by repeating the adjacent line. We note that making an entry larger than necessary to retain TN may be problematic, as, because of Sylvester’s identity, it may preclude a later choice to make all minors nonnegative, as the following simple example demonstrates:

Observe that if x is chosen positive, then no matter what nonnegative value is chosen for the (1,1) entry the resulting matrix will not be TN.

We then have

Theorem 9.0.1 Let and . Any m-by-n TP (resp. TN) matrix occurs as a submatrix of an m-by-n one in any desired contiguous positions.

If we ask, instead, to increase the size of a given TN (or TP) matrix by inserting a line between two given adjacent lines, this is easy in the TN case by making the new line 0 or repeating one of the adjacent lines. The TP case of line insertion is more interesting and requires a careful argument. This was carried out in [JS00] to produce the following result.

Theorem 9.0.2 Let and . Given any m-by-n TP (resp. TN) matrix A, there is an m-by-n TP (resp. TN) matrix B such that A is a submatrix of B in any desired m rows and n columns.

9.1 COMPLETIONS AND PARTIAL TN MATRICES

We say that a rectangular array is a partial matrix if some of its entries are specified, while the remaining, unspecified, entries are free to be chosen. A partial matrix is partial TP (TN) if each of its fully specified submatrices is TP (TN). A completion of a partial matrix is a choice of values for the unspecified entries, resulting in a conventional matrix that agrees with the original partial matrix in all its specified positions. Of course, for a completion of a partial matrix A to be TP (TN), A must have been partial TP (TN). It is a question of interest which partial TP (TN) matrices have a TP (TN) completion. It is not the case that every partial TP (TN) matrix has a TP (TN) completion.

Example 9.1.1 Let

It is then easily checked that A is partial TP, but A has no TN completion. To see this, suppose that

is a completion of A. Then

which is always negative for .

It is natural to ask which patterns for the specified entries of a partial TP (TN) matrix guarantee that a partial TP (TN) matrix has a TP (TN) completion. From the discussion of bordering/line insertion, we already know some: those partial TP (TN) matrices whose unspecified entries constitute a collection of lines. Another simple example is the following.

Example 9.1.2 Let

be a 3-by-3 partial TN matrix in which the entries a_ij are specified and . Then the completion

is TN (easily checked). If A is partial TN with , then a₂₁ or a₁₂ must be zero and a₂₃ or a₃₂ must be zero, in which case the completion,

is TN. We will see that this strategy for a TN completion generalizes nicely. If A is partial TP, the completion will not be TP (only TN, as the upper left and lower right 2-by-2 minors are 0), but one nearby (with slightly smaller (1,3) and (3,1) entries) is TP.

In the case of other completion problems (such as the positive definite one [GJSE84]), square, combinatorially symmetric (the i,j entry is specified if and only if the j,i one is) patterns play a fundamental role.

We digress here to mention a result in the case of positive (semi-) definite completion theory for comparison purposes. Since the positive semidefinite work occurred earlier, it also provided a backdrop for the TN work that we mention. Since positive semidefinite matrices are necessarily symmetric (Hermitian), the specified entries of a partial matrix may always be identified with an undirected graph, and since the property of being positive semidefinite is inherited by principal submatrices, a partial Hermitian matrix must be partial positive semidefinite (all fully specified principal submatrices are positive semidefinite) to have a chance at a positive semidefinite completion.

This raises the question of which graphs (for the specified entries, the definition will follow) ensure that a partial positive semidefinite matrix has a positive semidefinite completion. The answer is exactly the chordal graphs [GJSE84]. An undirected graph is chordal if it has no induced cycles of length 4 or more (that is, any long cycle has a “chord”), but the chordal graphs may also be characterized as sequential “clique sums” (identification along a clique) of cliques. (Recall that a clique is also known as a complete graph, or a graph that includes all possible edges.) The MLBC graphs, to be defined, are special chordal graphs in which, not only is there labeling of vertices, but the sequential clique summing is “path-like” and the summing is always along a clique consisting of just one vertex.

In the TN case, the question of which square, combinatorially symmetric patterns with specified diagonal insure that a partial TN matrix has a TN completion has been settled. A key component is the following special completion problem that generalizes Example 8.1.1. Consider the partial matrix

in which A₁₁ is n₁-by-n₁, A₃₃ is n₃-by-n₃, and a₂₂ is a scalar. If A is partial TN (that is, and are TN) and , then the completion

is TN (see [JKL98]). (Note that a₁₂ is n₁-by-1, is 1-by-n₃, is 1-by-n₁, a₃₂ is n₃-by-1, so that is n₁-by-n₃ and is n₃-by-n₁.) This is so by observing that

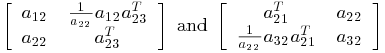
are nonnegative and of rank one, so that, by Sylvester’s determinantal identity, and, by induction on , is TN. In case A is partial TN and , there is also a TN completion (see [DJK08]).

9.2 CHORDAL CASE—MLBC GRAPHS

The pattern of a combinatorially symmetric n-by-n partial matrix with specified main diagonal may be described with a simple undirected graph on n vertices (which in our case can always be represented as ). There is an undirected edge (often interpreted as an unordered pair from ) between vertices i and j if and only if the (i,j) entry, with , is specified. A monotonically labeled block-clique graph (an MLBC graph) is a labeled, undirected graph, in which each maximal clique (complete, induced subgraph) is on consecutively labeled vertices, and each two cliques that intersect (vertex-wise) intersect in exactly one vertex which is the highest labeled in one of the cliques and lowest labeled in the other. The maximal clique containing vertex 1 and each other maximal clique, except the one containing vertex n, has a successor clique, so that the maximal cliques may be viewed as in a line and numbered , if convenient. For example, Figure 9.1 shows a MLBC graph on 11 vertices with four maximal cliques: , , , and , connected (or summed) along vertices 3, 6, and 7. As mentioned above, it is clear that an MLBC graph is just a special case of a chordal graph.

Figure 9.1 MLBC graph on 11 vertices

In general, the pattern of the specified entries of an n-by-n partial matrix with specified main diagonal entries may be described by a directed graph G on vertices , in which there is a directed edge (or arc) (i,j) from i to j if and only if a_ij is specified. In case the partial matrix is combinatorially symmetric, the graph of the specified entries may be taken to be undirected (as seen above). A key issue when considering TN completion problems and the graph of the specified entries than the labeling of the vertices. This is because TN is not closed under arbitrary permutations, so the same graph with a different labeling yields a (possibly) different completion problem, and often a much different result.

A partial matrix with the 11-vertex MLBC graph in Figure 9.1 as the graph of its specified entries would then have the form

where x represents a specified entry and ? represents and unspecified entry, as usual.

Note that the partial matrix

discussed earlier has the MLBC graph on vertices with just two maximal cliques of and vertices, respectively. As indicated above, if A is partial TN, then A has a TN completion (a special completion was provided above). Now, if a partial TN matrix has a general MLBC graph for its specified entries, with maximal cliques, it is not difficult to see inductively that it also has a TN completion. First, complete the square partial submatrix corresponding to the first two maximal cliques (say starting from the one that contains the vertex labeled 1). The resulting partial matrix is still partial TN but now has k-1 maximal cliques, and reduction to the case of two maximal cliques (done above) shows completability. Interestingly, such patterns are the only ones for which a partial TN matrix is necessarily completable, among square, combinatorially symmetric patterns with a specified main diagonal (see [JKL98] and [DJK08]).

Theorem 9.2.1 All square, combinatorially symmetric partial TN matrices with specified main diagonal and with G as the labeled undirected graph of its specified entries have a TN completion if and only if G is MLBC.

The proof of sufficiency of the condition was outlined above. Necessity of the condition is proven by an intricate collection of noncompletable, partial TN examples that may be found in [JKL98], where sufficiency was first proven. The case in which some diagonal entries are zero was given in [DJK08].

Because the property TP depends so much upon the entire matrix, there does not appear to be a simple way to move easily between TN and TP completability theory ([JN09] notwithstanding). For example, a complete result in the partial TP case, analogous to Theorem 8.3.1, is not known at present. However, it has been shown that the MLBC condition is sufficient for TP completability of partial TP matrices. The proof, however, is much more intricate [JN09].

Theorem 9.2.2 Let G be an MLBC graph on n vertices. Then every n-by-n partial TP matrix, with specified main diagonal, the graph of whose specified entries is G, has a TP completion.

When the specified entries of a partial matrix do not align as a MLBC graph (including noncombinatorial symmetry, nonsquareness and the possibility that some diagonal entries are not specified), some partial TN (TP) matrices may and some may not have a TN (TP) completion. The difficulty, at present, is if there is a way to tell. According to real algebraic geometry ([BCR98]), the TN or TP matrices form a semi-algebraic set in real matrix space, that is, membership may be described by a finite list of polynomial equalities and/or inequalities in the entries. The definition by nonnegativity or positivity of minors suffices for this. It follows from the Tarski-Seidenburg principle that a projection of a semi-algebraic set onto a subspace is also semi-algebraic. Using this, it follows that for any fixed pattern of the specified entries, there is a finite list of conditions, polynomial inequalities in the specified entries, that are necessary and sufficient for the existence of a TN (TP) completion. In general, however, it is quite difficult to generate a good list of conditions, though it is convenient to realize that such a list exists. A list might be found using Gröbner bases in computational algebra, but such procedures quickly become computationally prohibitive. The MLBC result, Theorem 8.3.1, may be viewed as a case in which the conditions that the partial matrix be partial TN (these are polynomial, as each fully specified minor is a polynomial in its entries and must be nonnegative).

There are situations in which nice conditions are known and we close this chapter by mentioning a selection of such results along with other completion results.

9.3 TN COMPLETIONS: ADJACENT EDGE CONDITIONS

The simplest connected, undirected graph, corresponding to a pattern with specified diagonal, that is not an MLBC graph shown in Figure 9.2, corresponding to the partial matrix

Figure 9.2 Labeled path on 3 vertices—Non-MLBC

with x and y unspecified. For A to be partial TN (TP), we must have

In the TP case, for example, we may assume, without loss of generality by diagonal scaling, that . For to be positive, we must then have

and for ,

In order that both inequalities hold, we must have

or

Thus, for the adjacent edges and , the edge product with the “outer” indices is required to be smaller than the one with the inner indices. Thus, this was called the adjacent edge conditions in [DJK08]. On the other hand, if the adjacent edge condition holds, the completion

is easily checked to be TP and is TP, as

by Sylvester’s determinantal identity. The TN case with positive main diagonal is similar. We summarize the 3-by-3 case as follows.

Theorem 9.3.1 If A is a partial TN (TP) matrix with ones on the main diagonal and the graph of its specified entries is the graph from Figure 9.2, then A has a TN (TP) completion if and only if the adjacent edge condition

holds.

Of course, there is a similar condition

for the graph in Figure 9.3.

The key point is that the edge with indices closer together has larger product. For an n-by-n partial matrix, such adjacent edge conditions are necessary for completability because the properties TN and TP are inherited by submatrices. This means that the adjacent edge conditions are necessary in general (see also [DJK08]).

Figure 9.3 Another labeled path on 3 vertices—Non-MLBC

Theorem 9.3.2 Let A be an n-by-n partial TN (TP) matrix with ones on its main diagonal and G as the graph of its specified entries. Then a necessary condition for A to have a TN (TP) completion is that whenever undirected edges and occur with either or in G, we must have the adjacent edge conditions

Implicitly in these results, it is assumed, even in the TN case, that the main diagonal entries are all positive. If, however, a main diagonal entry is 0, then the other forced zeros may be exploited to simplify certain completions problems. In [DJK08] (and earlier in [DJ97]) graphs are discussed for which the adjacent edge conditions, in addition to partial TN (TP), are sufficient for TN (TP) completion.

Typically, more than the adjacent edge conditions are needed. The case of a 4-cycle, as the graph of the specified entries, is an illustrative, small example. Consider the case in which the vertices of the cycle are numbered consecutively (as in Figure 9.4). We first note that, in a general n-by-n TN matrix with ones on the main diagonal, we have such inequalities as

Figure 9.4 A 4-cycle with vertices labeled consecutively

This simply follows from just TN by working outward from the main diagonal. Specializing and using the transposed inequality, it follows that for the partial TN matrix

(the graph of whose specified entries is the one in Figure 9.4) to have a TN completion, we must have

and

Remarkably, these conditions are sufficient for TN completability. If a₁₂ or a₂₁ is zero, the problem quickly reduces to a simpler one. If both are positive, the very particular completion

is TN (see [JK10]). Also, interestingly, no more symmetric completion works, even if the data are symmetric!

This 4-cycle case may be used to initiate an induction in which a general n-cycle result is proven with the aid of the MLBC result (Theorem 8.3.1). For more details, the reader is urged to consult [JK10], which includes the next result.

Theorem 9.3.3 Let G be the sequentially labeled cycle on n vertices. A partial TN matrix , with ones on its main diagonal and graph G for its specified entries, has a TN completion if and only if the two cycle conditions

and

hold

As indicated above, the proof in the n-by-n case relies on the 4-by-4 case outlined. Suppose A is an n-by-n partial matrix with specified entries as presented by

with the assumed necessary conditions and .

In the position, we put and in the position, we insert . So at this point our partial matrix has the form:

We may now complete the lower right (n-1)-by-(n-1) block by induction. Having completed this block, we may view the remainder of the completion, namely the unspecified entries in the first column and the unspecified entries in the first row, as completing an MLBC graph consisting of two cliques.

We also note that a similar result holds in the TP case as well, with analogous necessary conditions. The proof in the TP case, found in [JK10], is similar to the TN case above, but requires a far more delicate bordering technique that we omit here. The result, however, can be stated as (see [JK10]),

Theorem 9.3.4 Let G be the sequentially labeled cycle on n vertices. A partial TP matrix , with ones on its main diagonal and graph G for its specified entries, has a TP completion if and only if the two cycle conditions

and

hold.

9.4 TN COMPLETIONS: SINGLE ENTRY CASE

We continue this chapter by relaxing the conditions of combinatorial symmetry of the partial matrix and squareness of the matrix entirely. A natural question, then, is for which single entries does every partial TP matrix with that unspecified entry have a TP completion? Suppose the pattern is m-by-n. The and (m,n) entries play a special role; they are unbounded above as they enter positively into every minor in which they lie. Thus, if either of these is the single entry, then a TP completion is always possible. In addition, we can make this more precise in the following manner, which will be useful in what follows.

Lemma 8.5.1 Let

be a partial TP matrix in which x is the only unspecified entry. Then, if x is chosen so that , we must then have that , (In particular, x>0.)

Proof. The proof follows inductively using Sylvester’s identity (1.5) for determinants applied to the leading principal minors of A in decreasing order of size. For example,

and since A is partial TP, we have that . If A is replaced by in the above identity, then it follows that , etc.

On the other hand, consider the partial matrix

To make its determinant positive, it has to be that , so that no TP completion is possible, as x>0. Thus, the entry cannot be such a single entry. This example may be bordered (as described at the beginning of this chapter) to give such an example for any and . The example

shows that the position also cannot be such an entry. To see this, observe that in order for to be positive we must have . But, then, is positive only if . Hence there can be no TP completion. Of course, the and are similarly excluded. These, in some sense, provide the dividing line, as was shown in [FJS00].

Before we come to the main result, we state and prove a very interesting observation that was not only needed for the proofs in [FJS00], but is also a fact that seems to arise in a number of places in the theory of total positivity (e.g., eigenvectors of TP matrices).

Lemma 9.4.2 Let be an (n-1)-by-n TP matrix, with a_i representing the ith column of A. Then, for

(9.1)

has a unique solution y for which

Proof. If k=1, (9.1) has solution

and . If , then (9.1) has solution

and we see that if k is odd, , while if k is even,

Getting back to single entry completion problems, the case when m=2 is quite elegant, and as such, we include it here for reference.

Lemma 9.4.3 Let A be a 2-by-n partial TP matrix with exactly one unspecified entry. Then A is completable to a TP matrix.

Proof. By reversing the indices we may assume, without loss of generality, that

Since A is partial TP, it follows that for i<j and distinct from k. Then, if we choose x such that , the resulting completion of A is TP.

We now state and include a proof of just one case of the main result of this section (the remainder of the argument, along with many other related facts, can be found in [FJS00]).

Theorem 9.4.4 Let A be an m-by-n partial TP matrix with only one unspecified entry in the (s,t) position. If , then A has a TP completion. If , then any such A has a TP completion if and only if or .

Proof. As stated above we only consider one case, and we assume for simplicity’s sake that . Suppose . Then let

By Lemma 9.4.2, in which .

Let , with x_B chosen so that Thus, and, by Lemma 8.5.1, we then have in particular, . So

Applying Sylvester’s identity (1.5) for determinants, we obtain det A>0 and we can continue to apply this identity to obtain:

We can then increase x_B (so as to make and obtain a TP completion of A.

To close this section, we include some further interesting and related discussion. For , consider partial m-by-n TP matrices with exactly two unspecified entries. We note that completing a 2-by-n partial TP matrix with two unspecified entries follows easily from Lemma 8.5.2. For the case when , all such completable patterns have been characterized in [FJS00]. For example, all partial 3-by-3 TP matrices with exactly two unspecified entries are completable except for the following four patterns:

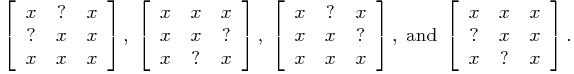
Finally, recall from earlier in this section we demonstrated that the and entries do not correspond to positions for which every partial TP matrix with that unspecified entry have a TP completion. However, curiously, it is a fact that if A is a partial TP matrix with both the (1,4) and (3,2) entries unspecified, then A may be completed to a TP matrix (see [FJS00]).

9.5 TN PERTURBATIONS: THE CASE OF RETRACTIONS

We have already seen that if we increase the (1,1) or the (m,n) entry of an m-by-n TN (TP) matrix, then the resulting matrix is TN (TP). In this section we investigate further which entries of a TN (TP) matrix may be perturbed (that is, increased or decreased) so that the result is a TN (TP) matrix. Suppose A is an n-by-n matrix. Then . Therefore, if , then , when . We are now in a position to make the following definitions on retractions and retractable sets, and we direct the reader to [FJ07] where some recent work on this topic was considered for various positivity classes of matrices, including TN.

Definition 9.5.1 Let denote a given subclass of the n-by-n P₀-matrices, and suppose A is an n-by-n matrix. Then we define

(i) — “the set of retractions of A”,

(ii) : — “the retractable subset of ”,

(iii) — “the set of all retractions of matrices in ”.

If, in (i), , then the interval for t is defined to be the single point zero. The notions of retraction (of a matrix) and retractable sets are very important for studying certain determinantal inequalities, such as Oppenheim’s inequality for entrywise (or Hadamard) products, see, for example, Section 8.3 within this work. It is known (see [FJ07]), and is not difficult to prove, that if = PSD, the set of all positive semidefinite matrices, then . Also if = M, the set of all M-matrices, then . A somewhat more subtle result is that if = TN, the set of all TN matrices, then . This fact will follow immediately from the next lemma which can also be found in [FJS00].

Lemma 9.5.2 Let A be an n-by-n TN matrix with . Then is TN for all .

Proof. First, observe that for every value ,

as . Recall that A admits a UL-factorization (follows from the LU-factorization result and reversal) into TN matrices (see Chapter 2). Partition A as follows,

where a₁₁ is 1-by-1 and . Partition L and U conformally with A. Then

Consider the matrix , with . Then

if . Note that if , then L, and hence A, is singular. In this case x=0 is the only allowed value for x. But, then, the desired result is trivial. Thus we assume that . To show that is TN, it is enough to verify that . Since if this were the case, would be TN, and, as L is TN by assumption, we have that their product, , is TN. Since and , it follows that L and U₂₂ are nonsingular. Hence , from which it follows that .

Note that a similar result holds for decreasing the entry by considering the matrix , which reverses both the row and column indices of A.

Corollary 9.5.3 Let TN denote the class of all n-by-n TN matrices. Then .

For the remainder of this section we restrict ourselves to the set of TP matrices. The first result for this class is a slight strengthening of Lemma 9.5.2 (see [FJS00]). Recall that an n-by-n triangular matrix A is said to a triangular TP matrix, ΔTP, if all minors of A are positive, except for those that are zero by virtue of the zero pattern of A. (Recall the definitions of TN_k and TP_k from Chapter 0.)

Theorem 9.5.4 Let A be an n-by-n TP matrix. Then is a TP matrix, for all .

Proof. Following the proof of Lemma 9.5.2 we can write

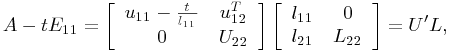
where , and both U,L are triangular TP matrices (see [Cry76] or Chapter 2). If , then and L are triangular TP matrices and hence is TP. So consider the case , or equivalently, , or . Let . Observe that and are TP matrices since A is TP. Thus the only contiguous minors left to verify are the leading contiguous minors of B. Consider the submatrix for . Then This minor is positive if and only if

which is equivalent to , an example of a Koteljanskii inequality (recall this from Chapter 6). The only issue left to settle is whether equality holds for the above Koteljanskii inequality. We claim here that for a TP matrix every Koteljanskii inequality is strict. Suppose the contrary, that is, assume there exist two index sets α and β such that . For simplicity, we may assume that ; otherwise replace A by in the following. By Jacobi’s identity (1.2), we have

Let , for . Then C is TP and the above equation implies . By a result in [Car67], C is reducible, which is nonsense since C is TP. Thus is TP, by Fekete’s criterion (see Corollary 3.1.5). This completes the proof.

It can be deduced from the proof above that is TP for all , and is TP when . An obvious next question is what other entries can be increased/decreased to the point of singularity so that the matrix is TP? As it turns out retracting (or decreasing) the (2,2) entry of a TP matrix results in a TP matrix as well (see [FJS00]).

Theorem 9.5.5 Let A be an n-by-n TP matrix. Then is TP for all .

Proof. Using the fact that all Koteljanskii inequalities are strict, it follows that all the leading principal minors of are positive. Consider the submatrix . To show that B is TP, we need only consider the contiguous minors of B that involve the first and second row and first column, as all other minors are positive by assumption. Let C denote such a submatrix of B. To compute , expand the determinant along the second row of C. Then

where is some minor of A. Thus is a positive linear combination of minors of A, and hence is positive. Therefore B is TP. Similar arguments show that is TP. This completes the proof.

A similar fact holds for the retraction of the entry of a TP matrix. The next result follows directly from Theorems 9.5.4 and 9.5.5.

Corollary 9.5.6 Let . If A is an n-by-n TP matrix and , then is TP for all .

According to the next example, we cannot decrease any other interior main diagonal entry (in general) of a TP matrix and stay TP (see [FJS00]).

Example 9.5.7 Consider the following matrix

Then A is a TP matrix with . However,

Thus for , we have , and hence is not TP.

Up to this point we have only considered retracting on a single diagonal entry. An obvious next step is to consider increasing or decreasing off-diagonal entries in a TP matrix. We begin a study of perturbing off-diagonal entries by considering the (1,2) entry (see also [FJS00]).

Theorem 9.5.8 Let A be an n-by-n TP matrix. Then is TP for all .

Proof. Since the (1,2) entry of A enters negatively into we increase a₁₂ to so that . Observe that the submatrix is equal to and hence is TP. Moreover, is TP since we have increased the “(1,1)” entry of a TP matrix. The only remaining minors to verify are the leading principal minors of . The nonnegativity of these leading minors follows from Sylvester’s identity (1.5). Hence . Replacing by in the above identity yields and so on. This completes the proof.

Using transposition and reversal, the conclusion of Theorem 9.5.8 holds when the (1,2) entry of a TP matrix A is replaced by the (2,1), and entries of A. Unfortunately, this is all that can be said positively concerning increasing or decreasing off-diagonal entries. Consider the following example which can also be found in [FJS00].

Example 9.5.9 Let

Then

Thus for , . Hence is not TP.

Similar examples can also be constructed in the case of the (2,3) and (1,4) entries, and consequently in all remaining off-diagonal entries of an n-by-n TP matrix.