11
Hybrid Systems
Basically, we have already applied the hybrid theory in preceding sections, for example Section 7.4. In many cases there were deterministic systems in the junction, for example a plate that we have considered as deterministic connection between the two cavity SEA systems and using the deterministic transfer matrix of the plate.
The twin chamber is an excellent test case for the hybrid method, as it constitutes a clear separation between random and deterministic subsystems and provides all the details of how to deal with each single step of hybrid FEM/SEA simulation.
11.1 Hybrid SEA Matrix
For pure SEA models the matrix from equation (6.113) is applied. The hybrid SEA matrix is similar except one additional damping contribution caused by the damping from the connected FEM-subsystems.
 (7.35)
(7.35)All other impacts of the FE parts of the hybrid model are hidden in the hybrid coupling loss factors or an additional power input that may come from radiation of FE-subsystems into the SEA-subsystems.
11.2 Twin Chamber

Figure 11.1 Twin chamber arrangement for TL tests of panel.
Source: Alexander Peiffer.
The twin chamber set-up is such a perfect example for the hybrid method, because both chambers are designed to be random by the large size and irregular shape. So, the two cavities can be considered as random subsystems for the complete frequency range. The panel that should be tested is supposed to be smaller than the panel from section 10.2.1. In this case it is not random and must be treated as a deterministic subsystem. We use the analytical solution of rectangular plate normal modes in the discrete version (5.41). As described in section 1.4.4.1 the normal modes are given as vectors and assembled in a matrix
and the deterministic equations of motion are transformed into diagonal form. For the flat plate we use the mode shapes from equation (5.46) so that we can write the deterministic dynamic stiffness matrix in the following form
 (11.1)
(11.1)The radiation stiffness is calculated using (8.42) and also transformed into the modal space by
The global form of the coupling loss factor and the transmission coefficient remains unchanged
 (7.50)
(7.50)The modal total stiffness matrix
requires some comment. The modal form of the direct radiation stiffness is a fully populated but symmetric matrix. Thus, the hybrid method destroys the diagonal form of the dynamic stiffness matrix. Though the introduction of random systems reduces the degrees of freedom tremendously, the computational amount can be higher than for a full deterministic method if the connecting regions are too large. See Peiffer (2012) for details. In Figure 11.2 the subsystem configuration is shown. We chose a rather small flat aluminium plate of size m and m of 4 mm thickness. At this size we will have a deterministic behaviour until 2 kHz.

Figure 11.2 System and loads setup for the hybrid twin chamber model.
Source: Alexander Peiffer.
The damping in the SEA systems due to the connected FE subsystems is given by (7.52)
This damping loss corresponds to the dissipation in the cavities because of energy dissipated in the connected FEM plate. In comparison with the situation when the plate is an SEA subsystem, this part replaces the dissipation in the reverberant field of the plate.
For the execution of the full hybrid simulation process, we apply a random power load to the first SEA cavity and a deterministic out-of-plane point force at the plate near the corner. This creates the typical setup where we need both the random modelling of the reverberant fields in the cavity and the deterministic model of the plate. The random point force (3.230) will not provide a good estimation of the real input power, because the plate is a deterministic subsystem. Thus, the modal frequency response to this force excitation must be used. To summarize, two load cases are simulated:
Power 1W Power source in cavity 1
Force 10 N rms Point force on plate.
The global set-up of cavities is the same as in Chapter 10. The plate shall be deterministic for a large frequency range. In order to cover the coincidence region, we aim at calculating the frequency response up to f=4000 Hz. The hybrid modelling example is also useful for further clarification when and under which conditions the SEA assumptions become valid. Thus, all results will be compared to the results of an SEA model with the same data.
11.2.1 Step 1 – Setting up System Configurations
The normal modes of the plate are taken from equation 5.46. The modes are sorted in frequency order. The first mode shape with is at Hz; until Hz there are 140 modes. The SEA properties of the cavities are taken from Chapter 10.
The direct field radiation stiffness matrices are calculated using a mesh of and nodes. This leads to a mesh of element length m, which is sufficient for this frequency. When the structural plate modes shall be calculated using a FE-mesh, this must be fine enough for the bending wavelength and can thus be much finer than the mesh that is required for a precise radiation stiffness calculation in the desired frequency range. However, in this example it is not necessary, because we map the solution onto our mesh directly from analytical results.
When using fine FE meshes for the structure, it is better to use two meshes, each appropriate for structure and fluid, for the better use of (8.42).
11.2.2 Step 2 – Setting up System Matrices and Coupling Loss Factors
The total system matrix is created according to (11.3). All degrees of freedom are shared by the connected systems and no specific treatment of connecting region is required.
The SEA matrix is set up with the same principles as in section 7.3.2.1 and using equation (7.50). In the SEA matrix the plate does not occur as subsystem. Hence, for the energy degrees of freedom, we have a two system SEA matrix.
The result for the hybrid transmission loss of the plate is shown in Figure 11.3. In addition the SEA transmission loss is also included. We recognize the typical shape of the transmission loss as described, for example, in Bies et al. (2018). At low frequencies below the first resonances, the transmission is stiffness controlled and very high. The transmission loss drops down at the first panel resonances, increases, and reaches mass law slope above 500 Hz. At this frequency the wavelength in the fluid becomes similar to the panel dimensions. There is a good agreement between the SEA and the hybrid result in the mass law regime. In the coincidence area both curves also coincide well, despite small variations around the ensemble average of the SEA curve. Thus, the reverberant field model of the plate and area coupling loss factors are in good accordance to the hybrid method.

Figure 11.3 Hybrid and SEA transmission loss of aluminium plate.
Source: Alexander Peiffer.
In addition to the inert damping of the SEA systems, there is the damping due to the connected FEM subsystems given in modal form by (7.51). The damping loss for both cavities is shown in Figure 11.4, revealing that this dissipation is relatively low. The reason for the low dissipation is the small area of the panel in relation to the total surface of the room. When all walls of the room would be FEM subsystems, the situation would be different. The highest dissipation occurs at the resonances of the plate.

Figure 11.4 Damping loss in both cavities due to coupled FEM system.
Source: Alexander Peiffer.
11.2.3 Step 3 – External Loads
First, the SEA cavity 1 is excited by a power load of W. Second, the plate is excited by a point force in the -direction of the plate with N that is located at m and m in plate coordinates assuming one corner as origin. Both cases are calculated separately.
11.2.4 Step 4 – Solving System Matrices
11.2.4.1 Step 4.1 – Power Input due to FEM System Excitation
The cross spectral density of the point force in modal coordinates must be calculated with
and the radiated power with
Even in modal form the triple matrix multiplication of (11.4) is computationally expensive. As the point force is fully coherent (to itself), it is faster to calculate the cross spectral density of the plate from the deterministic response, hence solving
calculating the cross spectral density directly from the deterministic response, and determining the power input into the SEA subsystems from external excitation that is not related to SEA. The rms-value N of the point force corresponds to an amplitude of N. From the above equation we calculate a power radiation from the plate into the SEA systems as given in Figure 11.5. Compared to the source in cavity 1, the power can be neglected. However, at the odd resonances and near coincidence the panel becomes an efficient radiator, leading to high power radiation into the cavities. As both cavities are directly connected to the vibrating plate, the power radiation is the same for both rooms.

Figure 11.5 Power input to both rooms from deterministic force excitation at the plate.
Source: Alexander Peiffer.
The velocity rms-value is reconstructed from the modal coordinates by
The resulting velocity due to the force excitation is shown in Figure 11.7 in combination with the velocity caused by excitation from the reverberant fields.

Figure 11.7 Velocity of the plate due to power excitation in room 1 (LHS) and force excitation on plate (RHS).
Source: Alexander Peiffer.
11.2.4.2 Setp 4.2 – Solve the SEA Equations with SEA and FEM Power Input from Step 4.1
The result for each single case can be seen in Figure 11.6. In comparison the power load in cavity 1 leads to higher pressure levels at low frequencies, but at high frequencies the radiation from the plate becomes more efficient and radiates more energy into cavity 2 than is transmitted from cavity 1 into cavity 2 through the plate. The SEA results of the corresponding model show that the random modelling gives reliable results above 600 Hz for the power excitation in cavity 1 and above 2 kHz for the force excitation. In case of force excitation, the point force does not lead to equal excitation of all modes, and the conditions for SEA are met later in frequency. In addition we must consider that the mass law provides a correct value for the coupling of both cavities, and therefore the results agree earlier in frequency with the hybrid result.
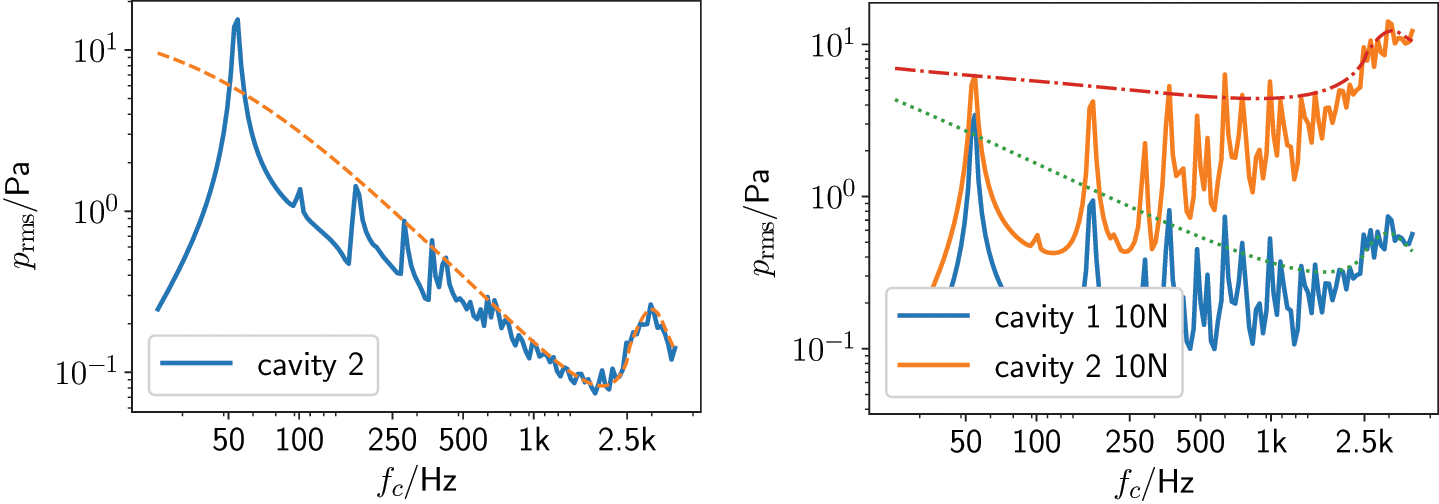
Figure 11.6 Pressure in both rooms due to power excitation in cavity 1 (LHS) and force excitation on plate (RHS).
Source: Alexander Peiffer.
11.2.4.3 Step 4.3 – Calculate FE Response due to Energies in SEA Subsystems from Step 4.2
As the external forces were treated by step 4.1, we finally calculate the response of the FEM systems resulting from the reverberant field excitation in each subsystem using (7.43), omitting the deterministic external loads
As the response is calculated in the modal base, the cross spectral density matrix must be converted into the mesh space by
and the rms-velocity results from the diagonal of the above matrix
11.2.5 Step 5 – Adding the Results
In the final step all results are added together for the deterministic systems. The cross spectral density of the plate results from the external excitation and the reverberant load of the connected SEA systems. In Figure 11.7 the rms-velocity of the plate is shown in combination with the SEA result. For the power load case there is no external excitation of the plate, so the reverberant load is the exclusive excitation. The SEA simulation covers only the resonant energy in the plate. This is the reason why both curves don’t agree even at high frequencies, and the resonant SEA solution underestimates the velocity level compared to the FEM system response. When we add the nonresonant motion to the engineering result of the plate using (10.19), both curves agree well above 500 Hz.
In case of the force excitation, the external load response is dominant compared to the reverberant response . This is obvious, because the reverberant load from the cavities is the indirect feedback of the force exciting the plate. Globally, the results from section 6.4.2.1 are still valid. A point force requires a large modal overlap to fulfil the conditions of a smooth ensemble average. However, above 1kHz the SEA solution is valid.
11.2.5.1 Conlusions
We can perform a Monte Carlo analysis with our test case by generating an ensemble average of different realizations of the plate, and we would get a smoothly averaged result as shown in Shorter and Langley (2005). The example indicates how useful the hybrid theory is, especially for transmission loss calculations, as these cases provide nearly perfect separation between the random systems (cavities) and the deterministic plate. In addition the hybrid theory illustrates the limits of SEA. The modal and resonant dynamics of the plate cannot be modelled by SEA, whereas the high frequency dynamics can be calculated very efficiently without large losses in precision.
This is a rather academic case with simple cavities and a simple flat plate. When real systems or plates with irregularities, beadings, etc. are dealt with there may be more uncertainty in the system, and thus, the random approach becomes a more valid option in comparison to the natural uncertainty of the technical system.
11.3 Trim in Hybrid Theory
For the consideration of trim layers in hybrid theory, the degrees of freedom have to be reorganized in such a way that there are structural and fluid half space degrees of freedom as far as those of the two trim surfaces. In order to keep the derivation simple we consider the plate to be fully covered with noise control treatment.
As the FEM subsystem is modelled by a FEM matrix, a discrete form of the trim layer stiffness is needed. One option is to apply the porous finite element method (PEM) (Allard and Atalla, 2009). We will approximate the stiffness matrix of the noise control treatment by converting the wavenumber transfer matrix into the discrete regular meshed space by an inverse Fourier transform. This assumption is valid for large areas with constant lay-up over the area.
11.3.1 The Trim Stiffness Matrix
In order to cope with the hybrid theory, the acoustic treatment must also be modelled by a a stiffness matrix. This is rather unusual, as, for example, FE implementations are using displacement degrees of freedom for the structure side and pressure degrees of freedom for the fluid side (Doutres et al., 2007) due to the fact that the fluid is represented by pressure degrees of freedom in most solvers.
The trim dynamic stiffness matrix has different sets of degrees of freedom for the left (1) and right (2) side. This suggests writing the matrix in blocked form
The calculation of the above stiffness matrix is done in two steps: First, the transfer matrix of the infinite layer from section 9.3 is transformed into the stiffness matrix in wavenumber domain.
 (11.13)
(11.13)Second, this stiffness matrix must be converted into the discrete space. For the approximation of this discrete stiffness matrix, we assume a regular mesh with constant element lengths ,. The transfer matrix of infinite layers (9.96)
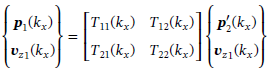 (9.96)
(9.96)is to be converted into the stiffness matrix (11.13). The internal pressure must be replaced by the external pressure
 (11.14)
(11.14)and the coefficients of the stiffness matrix in wavenumber domain are hence
In Figure 11.8 such a treatment connected to a structure is shown. Tournour et al. (2007) proposed a local approximation that assumes that only the opposite nodes are connected. This assumption is valid for very thin layers (), and the block matrices in equation (11.12) are diagonal in that case. It is shown by Peiffer (2018) that this assumption is too strict and a nonlocal approach is required for most treatments.

Figure 11.8 2D sketch of plate with trim.
Source: Alexander Peiffer.
This matrix must be converted into the space domain by inverse Fourier transform. Using the jinc-function approach from Langley (2007) and assuming isotropy in each layer, the transformation becomes simple and implies a finite wavenumber integration.
The transformation is applied to each coefficient of the stiffness matrix with wavenumber arguments
being the projected distance between nodes, and the maximum wavenumber that can be represented by the spacial sampling of the mesh, respectively. The integral in (11.18) is solved numerically, and the stiffness matrix of the trim is available for further considerations.
11.3.2 Hybrid Modal Formulation of Trim and Plate
The trim constitutes an additional deterministic layer that must be considered in the total stiffness matrix. When a layer of noise control treatment is applied to the right surface, the plate degrees of freedom are shared with those from left side of the trim. The right side of the noise control treatment is connected to the fluid as shown in figure 11.8.
This configuration gives rise to the following block matrix configuration
adding up to the total stiffness matrix with trim
The coupling loss factor can be calculated when we write (7.27) in block matrix form
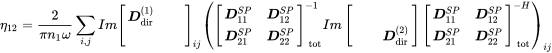 (11.22)
(11.22)The above equation can be used as is but leads to double size matrices in this case. The idea is to stay with the plate displacement coordinates and condense the above equation to pure structural coordinates, here . Writing equation (11.20) using the block matrix gives
We eliminate in order to express the total stiffness in structural coordinates. Doing this with equations (11.23) and (11.24) leads to
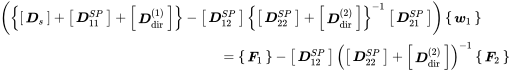 (11.25)
(11.25)There is a modified version of the total stiffness matrix
which is valid for coordinates Due to the condensation is transformed to degrees of freedom by
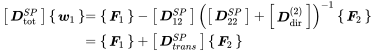 (11.27)
(11.27)using the transformation matrix
Equation (11.27) provides the deterministic equation of motion for displacement degrees of freedom of the plate. For use in hybrid coupling loss factor equation (7.27), we replace the direct radiation stiffness by an expression that includes the trim. Let us first consider that the trimmed side is the radiating side. The power radiated by the degrees of freedom from side two is given by
Reordering of (11.24) and assuming no external forces allows transforming to
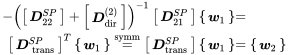 (11.30)
(11.30)and we get for the radiated power
The term between both is called the reduced radiation stiffness
Thus, the radiated power can be calculated with
 (11.33)
(11.33)and (11.32) replaces in equation (7.27).
From reciprocity (6.112) it follows that the reduced radiation stiffness can also be used for the reverse direction.
In addition to the reciprocity argument, the above expression can also be derived using the fact that in the condensed equation of motion (11.27), forces are converted to by the transformation matrix .
The diffuse field excitation from side two is then given by
 (11.36)
(11.36)Entering this expression in (7.21) leads also to (11.35). It can be shown that a trimmed surface can be considered in general by using the total stiffness matrix given by
using the different expression for trimmed sufaces
According to equations (11.34) and (11.35), the radiation stiffness must be replaced by the reduced radiation stiffness if there is trim on the surface. The same approach is used for all other expressions used in the hybrid formulation, for example (7.52).
11.3.3 Modal Space
The stiffness matrix must be transformed into the modal space for both sets of degrees of freedom. The transformation reads:
Or, in matrix form when we write all connecting region degrees of freedom in one column vector
The transformation matrix is a block matrix with twice the modal transformation matrix. All system matrices are transformed into modal space by this matrix meaning to apply the modal transformation matrix to every block matrix. All above given matrices are converted to modal space with the usual transformation.
The same is true for the block matrices of the trim leading to:
From the conversion to modal space follows a useful property for evaluating the radiation: the modal radiation efficiency given by
For configurations with trim the reduced radiation stiffness from equation (11.32) shall be considered.
11.3.4 Plate Example with Trim
We apply this theory to the plate from section 11.2. The panel surface connected to cavity 2 is treated with the 5 cm fiber-mass system from section 10.5.3. With the given theory the transmission loss is calculated and shown in Figure 11.8 in comparison with the SEA result. The agreement between hybrid and SEA is even better than for the untrimmed case. Both approaches start to coincide above 250 Hz in contrast to figure 11.3 where the agreement started around 1 kHz. This is the reason why SEA is considered often as valid even at low frequencies for airborne problems. The dissipation by the noise treatment introduces damping into the system that results in an earlier fulfillment in frequency of the requirements of SEA.

Figure 11.9 Transmission loss of small panel with trim, hybrid and SEA solution.
Source: Alexander Peiffer.
Bibliography
- Jean-F. Allard and Noureddine Atalla. Propagation of Sound in Porous Media. Wiley, second edition, 2009. ISBN 978-0-470-74661-5.
- David Alan Bies, Colin H. Hansen, and Carl Q. Howard. Engineering Noise Control. CRC Press, Boca Raton, fifth edition, 2018. ISBN 978-1-138-30690-5 978-1-4987-2405-0.
- Olivier Doutres, Nicolas Dauchez, and Jean-Michel Génevaux. Porous layer impedance applied to a moving wall: Application to the radiation of a covered piston. The Journal of the Acoustical Society of America, 121(1):206, 2007. ISSN 00014966.
- R. S. Langley. Numerical evaluation of the acoustic radiation from planar structures with general baffle conditions using wavelets. The Journal of the Acoustical Society of America, 121(2): 766–777, 2007.
- Alexander Peiffer. Comparison of the computational expense of hybrid FEM/SEA calculation. In Proceedings NOVEM 2012, Sorrento, Italy, April 2012.
- Alexander Peiffer. Hybrid modelling of transmission loss with acoustic treatment. In Fortschritte Der Akustik, pages 50–53, München, Germany, March 2018.
- P. J. Shorter and R. S. Langley. Vibro-acoustic analysis of complex systems. Journal of Sound and Vibration, 288(3): 669–699, 2005. ISSN 0022-460X.
- Michel A. Tournour, Fumihiko Kosaka, and Hirotaka Shiozaki. Fast Acoustic Trim Modeling using Transfer Admittance and Finite Element Method. In Proceedings SAE 2007 Noise and Vibration Conference, pages 2007–01–2166, May 2007.
