we may transform S so that

with e₁, e_m+1 =0,1,2or3 and a_i = 1 or 2 for i = 1,..., m and m > 0. Multiplying by a suitable power of X we obtain

with m > 0 and a =0,1,2 or 3. Assume that m > 1 and let

We show by induction that

or

This claim for the entries of S₁ is true for

Suppose it is correct for. Then

Therefore the claim is correct for all S₁ with m > 1. This gives a contradiction, for the entries of X^a with a =0,1,2 or 3 do not satisfy the claim. Hence m = 0 and S can be reduced to a trivial relation by the given set of relations. Therefore they are a complete set of defining relations and the theorem is proved. □

Corollary 9.6.11. The Modular Group M = PSL₂() has the presentation

Further x, y can be taken as the linear fractional transformations

Proof. The center of SL₂() is ±I. Since X² = -I setting X² = I in the presentation for SL₂()gives thepresentationforM. Writing the projective matrices as linear fractional transformations gives the second statement. □

This corollary says that M is the free product (see Section 9.9) of a cyclic group of order 2 and a cyclic group of order 3.

We note that there is an elementary alternative proof to the above Corollary as far as showing that X² = Y³ = 1 are a complete set of defining relations. As linear fractional transformations we have

Now let

Then

Let S € r. Using the relations X² = Y³ = 1 and a suitable conjugation we may assume that either S = 1 is a consequence of these relations or that

with 1 < a_i < 2 and a₁ = a_n.

In this second case if x eR+ then S(x) e R⁻ and hence S =1.

This type of ping-pong argument can be used in many examples (see [LS], [CRR], and [Jit]). As another example consider the unimodular matrices

Let Ā, B denote the corresponding linear fractional transformations in the modular group M. We have

In particular A and B have infinite order. Now

for all n ≠ 0. The ping-pong argument used for any element of the type

with all n_;, m_t = 0and n₁ + n_k+1 = Oshowsthat S(x) € R⁺if x € R⁻. It follows that there are no non-trivial relations on A and B and therefore the subgroup of M generated by A, B must be a free group of rank 2.

9.7 Presentations of Subgroups

Given a group presentation G = (X; R> it is possible to find a presentation for a subgroup H of G. The procedure to do this is called the Reidemeister-Schreier process and is a consequence of the explicit version of the Nielsen-Schreier theorem (Theorem 9.4.8). We give a brief description. A complete description and a verification of its correctness is found in [MKS], [LS], [Bau], or [CRR].

Let G be a group with the presentation (a₁,...,a_n; R₁ = ••• = R_k = 1>.LetH bea subgroup of G and T a Schreier system for G modulo H defined analogously as above.

Reidemeister-Schreier Process

Let G, H and T be as above. Then H is generated by the set

with a complete set of defining relations given by conjugates of the original relators rewritten in terms of the subgroup generating set.

In order to actual rewrite the relators in terms of the new generators we use a mapping T on words on the generators of G called the Reidemeister rewriting process. This map is defined as follows: If

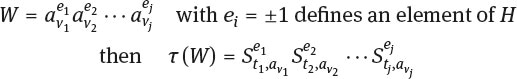
where t_{ is the coset representative of the initial segment of W preceding a_v. if e_i = 1 and tj is the representative of the initial segment of W up to and including a⁻¹ if e_t = −1. The complete set of relators rewritten in terms of the subgroup generators is then given ^by _-

We present two examples; one with a finite group and then an important example with a free group which shows that a countable free group contains free subgroups of arbitrary ranks.

Example 9.7.1. Let G = A₄ be the alternating group on 4 symbols. Then a presentation for G is

Let H = A4 the commutator subgroup. We use the above method to find a presentation for H. Now

Therefore |A₄ : A4| = 3. A Schreier system is then {1, b, b²}. The generators for A4 are then

while the relations are

(1)  T (aa) = S1aS1a = X²

(2)  T (baab⁻¹) = X^

(3)  T(b²aab-²) = Xj

(4)  T (bbb) = 1

(5)  T (bbbbb-¹) = 1

(6)  T(b²bbbb⁻²) = 1

(7)  T (ababab) = S^aSbia = X1X2X3

(8)  t (babababb⁻¹) = S_baS_b2_aS_1a = X₂X₃X₁

(9)  t(b²abababb~²) = S_b2_aS_1aS_ba = X₃X₁X₂

Therefore after eliminating redundant relations and using that X₃ = X₁X₂ we get as a presentation for A4,

Example 9.7.2. Let F = (x, y;) be the free group of rank 2. Let H be the commutator subgroup. Then

a free abelian group of rank 2. It follows that H has infinite index in F. As Schreier coset representatives we can take

The corresponding Schreier generators for H are

The relations are only trivial and therefore H is free on the countable infinitely many generators above. It follows that a free group of rank 2 contains as a subgroup a free group of countably infinite rank. Since a free group of countable infinite rank contains as subgroups free groups of all finite ranks it follows that a free group of rank 2 contains as a subgroup a free subgroup of any arbitrary finite rank.

Theorem 9.7.3. Let F be free of rank 2. Then the commutator subgroup F’ is free of countable infinite rank. In particular a free group of rank 2 contains as a subgroup a free group of any finite rank n.

Corollary 9.7.4. Let n, m be any pair of positive integers n, m > 2 and F_n,F_m free groups of ranks n, m respectively. Then F_n can be embedded into F_m and F_m can be embedded into F_n.

9.8 Group Decision Problems

We have seen that given any group G there exists a presentation for it, G = (X; R). In the other direction given any presentation (X; R) we have seen that there is a group with that presentation. In principle every question about a group can be answered via a presentation. However, things are not that simple. Max Dehn, in his pioneering work on combinatorial group theory about 1910, introduced the following three fundamental group decision problems (see [FR]):

(1)  Word Problem: Suppose G is a group given by a finite presentation. Does there exist an algorithm to determine if an arbitrary word w in the generators of G defines the identity element of G?

(2)  Conjugacy Problem: Suppose G is a group given by a finite presentation. Does there exist an algorithm to determine if an arbitrary pair of words u, v in the generators of G define conjugate elements of G?

(3)  Isomorphism Problem: Does there exist an algorithm to determine given two arbitrary finite presentations whether the groups they present are isomorphic or not?

All three of these problems have negative answers in general. That is for each of these problems, one can find a finite presentation for which these questions cannot be answered algorithmically (see [LS]). Attempts for solutions, and for solutions in restricted cases, have been of central importance in combinatorial group theory. For this reason, combinatorial group theory has always searched for, and studied, classes of groups in which these decision problems are solvable.

For finitely generated free groups there are simple and elegant solutions to all three problems. If F is a free group on x₁,...,x_n and W is a freely reduced word in x₁,...,x_n then W = 1 if and only if |W | > 1. Since freely reducing any word to a freely reduced word is algorithmic this provides a solution to the word problem.

Further a freely reduced word W = x^x^ ••• x^ is cyclically reduced if v₁ = v_n or if v₁ = v_n then e₁ = -e_n. Clearly then every element of a free group is conjugate to an element given by a cyclically reduced word called a cyclic reduction. This leads to a solution to the conjugacy problem. Suppose V and W are two words in the generators of F and V, W are respective cyclic reductions. Then V is conjugate to W if and only if V is a cyclic permutation of W.

Finally two finitely generated free groups are isomorphic if and only if they have the same rank.

The three problems listed above are only the basic decision problems and other algorithmic problems concerning presentations can be considered. The conjugacy problem asks to algorithmically determine if two elements given in terms of the generators are conjugate. The conjugator search problem asks: given a group presentation for G and two elements g₁, g₂ in G that are known to be conjugate to determine algorithmically a conjugator, that is an element h such that h~¹g₁ h = g₂.It is known, as with the conjugacy problem itself, that the conjugator search problem is undecidable in general.

The computational difficulty of solving various group decision problems will play the role of a hard problem used to construct a one-way function in several non-abelian group based cryptosystems. We will return to this idea in Chapters 10 and 11.

The book by Myasnikov, Shpilrain and Ushakov [MSU1] has discussions of the complexity of many of these group decision problems.

9.9 Group Amalgams

In analyzing the structure of an infinite discrete group via combinatorial group theory, group products or group amalgams are the key constructions. These constructions will not play a major role in the application of combinatorial group theory to cryptography but will occasionally arise. In this section we briefly introduce the basic definitions.

The general idea of group amalgams is to decompose (if possible) an infinite group G into an amalgam (in a way which we will describe shortly) of some of its subgroups. These subgroups are then called the factors of G. Information about G can then be deduced from the corresponding information on the factors. Thus amalgam decompositions play a role in infinite group theory similar to a prime factorization theorem, although the amalgam decomposition of a group G need not be unique.

There are essentially two different types of group amalgams: free products with amalgamation and HNN groups. An infinite group, however, may decompose as both a free product with amalgamation or in a different manner as an HNN group. Free products are a special case of free products with amalgamation, so we discuss these first.

Before beginning, we note that there are two main approaches to the theory of group amalgams. The first is a classical combinatorial approach which deals primarily with presentations for the group and its factors. The second approach is a geometric- topological technique which depends on how the group acts (as a group of isometries) on a graph. The second method is due to Bass and Serre. We refer to [LS], [Ser], or [CRR] for a more complete discussion of all of these.

Free products of groups are closely related to free groups in both form and properties. Let A = (a₁,...;R₁ = 1,...) andB = (b₁,...;S₁ = 1,...) be two groups. We consider the groups A and B to be disjoint. Then:

Definition 9.9.1. The free product of A and B denoted A * B is the group G with the presentation (a₁,...,b₁,...;R₁ = 1,...,S₁ = 1,...), that is, the generators of G consist of the disjoint union of the generators of A and B with relators taken as the disjoint union of the relators Rj of A and Sj of B. A and B are called the factors of G.

In an analogous manner the concept of a free product can be extended to an arbitrary collection of groups.

Definition 9.9.2. If A_a = (gens A_a; rels A_a), a e I , is a collection of groups, then their free product G = *A_a is the group whose generators consist of the disjoint union of the generators of the A_a and whose relators are the disjoint union of the relators of the A_a.

We saw as an example in Section 9.6.1 that the Modular group M = PSL(2, Z) is a free product of a cyclic group of order 2 and a cyclic group of order 3, that is M ≅ ₂ *Z₃.

Free products exist and are non-trivial. We have:

Theorem 9.9.3. Let G = A * B. Then the maps A → G and B → G are injections. The subgroup of G generated by the generators of A has the presentation (gens A; relsA), that is, is isomorphic to A. Similarly for B. Thus A and B can be considered as subgroups of G. In particular A * B is non-trivial if A and B are.

Free products share many properties with free groups. First of all there is a categorical formulation of free products. Specifically we have:

Theorem 9.9.4. A group G is the free product of its subgroups A andBifA and B generate G and given homomorphismsf₁ : A → H, f₂ : B → H into a group H there exists a unique homomorphism f : G → H extendingf₁ andf₂.

Secondly each element of a free product has a normal form related to the reduced words of free groups. If G = A * B then a reduced sequence or reduced word in G is a sequence g₁g₂ ••• g_n with g_{ = 1, each g_{ in either A or B and g_;, g_;+1 not both in the same factor. Then:

Theorem 9.9.5. Each elementg e G = A * B has a unique representation as a reduced sequence. The length n is unique and is called the syllable length. The case n = 0 is reserved for the identity.

A reduced word g₁ •••g_n e G = A * B is called cyclically reduced if either n < 1or n > 1 andg₁ andg_n are from different factors. Certainly every element of G is conjugate to a cyclically reduced word.

From this we obtain several important properties of free products which carry over to more general amalgams.

Theorem 9.9.6. An element of finite order in a free product is conjugate to an element of finite order in a factor. In particular a finite subgroup of a free product is entirely contained in a conjugate of a factor.

Theorem 9.9.7. If two elements of a free product commute then they are both powers of a single element or are contained in a conjugate of an abelian subgroup of a factor.

Finally, the following theorem of Kurosh extends the Nielsen-Schreier theorem to free products.

Theorem 9.9. (Kurosh). A subgroup of a free product is also a free product. Explicitly ifG = A * B and H c G then

where F is a free group and (* A_a) is a free product of conjugates of subgroups of A and (*Bp) is a free product of conjugates of subgroups ofB.

We note that the rank of F as well as the number of the other factors can be computed. A complete discussion of these is in [MKS] and [LS].

We now extend this construction to free products with amalgamation. Let A = (a₁,... ;R₁ = 1,...) and B = (b₁, ...;S₁ = 1,...) be two groups with H c A,K c B proper subgroups and f : H → K an isomorphism. Again we assume that A and B are disjoint. Then:

Definition 9.9.9. The free product of A and B amalgamating H to K is the group G with the presentation

that is the group G has as generators the disjoint union of the generators of A and B and has as relations the disjoint union of the relations of A and B together with an additional set of relations giving the subgroup isomorphism. Identifying H with its isomorphic image we say that G is the free product of A and B with H amalgamated denoted

The groups A and B are called the factors of G.

A group G is a (non-trivial) free product with amalgamation or amalgamated free product if G = G₁ *_H G₂ for some groups G₁ and G₂ both non-trivial and some proper non-trivial subgroup H in G₁ and also in G₂.

Taking H = {1} we obtain a free product. Therefore free products are just special cases of free products with amalgamation. As with free products, the factors inject into G and their intersection, as subgroups of G, is H, the amalgamated subgroup.

Theorem 9.9.10. Let G = A *_H B. Then A → G and B → G are injections. The subgroup of G generated by the generators of A has the presentation (gens A; relsA). Similarly for B. Thus A and B can be considered as subgroups of G and A n B = H.

The proof of this theorem depends upon a normal form for elements of free products with amalgamation. Let G = A *_H B and let L₁ be a set of left coset representatives for A modulo H and let L₂ be a set of left coset representatives for B modulo H, normalized in both cases by taking 1 to represent H. Then a reduced sequence or reduced word or normal form in G = A *_H B is a sequence of the form

where h e H, 1 = gj e L₁ u L₂ and g₁ •••g_n is a reduced word in the free product A * B, that is gj+1 i Li if gj e L_;.

Theorem 9.9.1. (Normal Form Theorem for Free Products with Amalgamation). IfG = A *_H B then everyg e G has a unique representation as a reduced sequence.

Extending the concept from free products, a reduced word g₁ • • •g_nh in G = A *_H B is called cyclically reduced if either n < 1or n > 2 and g₁ and g_n are from different factors. Certainly every element of G is conjugate to a cyclically reduced word. From this we obtain properties analogous to those in free groups and free products. Specifically:

Theorem 9.9.12.

(1)  An element ofG = A *_H B of finite order must be conjugate to an element of finite order in one of the factors. Thus a finite subgroup or more generally a bounded subgroup must be entirely contained in a conjugate of a factor.

(2)  An abelian subgroup ofG = A *_H Bis

(a)  a conjugate of an abelian subgroup of A or B or

(b)  a countable ascending union of conjugates of subgroups ofH or

(c)  a direct product of an infinite cyclic group and a conjugate of a subgroup ofH.

The concept of a free product with amalgamation can be extended in a straightforward manner to more than two factors.

Definition 9.9.13. Let {G_;}, i e I, be a family of groups. Let A be a group and for each i, fj : A → G_j a monomorphism. Then the free product of the G_j amalgamating A is the quotient group of the free product G = *_;G_; modulo the normal subgroup of *_;Gj generated by all relations f_j(a) = fj(a) with a e A and i, j e I.

As in the case of two factors, each Gj injects into G, and each element can be expressed as a normal form.

Before moving on to HNN groups we mention that there is also a categorical formulation of free products with amalgamation. Specifically;

Theorem 9.9.14. Suppose G is a group, G₁, G₂ subgroups and A a group together with injections 0₁ : A → G₁,0₂ : A → G₂. Then G = G₁ *_A G₂ if for every group H and every pair of homomorphisms f₁ : G₁ → H, f₂ : G₂ → H making the following diagram commute

there exists a unique homomorphism f : G → H extending f₁, f₂.

Our second basic amalgam construction is that of an HNN group. This construction has properties very nearly parallel to those of free products with amalgamation. As pointed out in [Ser], they are really two different aspects of the same idea.

Definition 9.9.15. Let G be a group, {A_;}, i e I, a family of subgroups of G, and for each i e I, fj : Aj → G a monomorphism. Then an HNN extension of G is a group G* of the form

G is called the base, {t_j}_jeI the free part or stable letters,and {A;, f_j(A_j)} the associated subgroups.

G* is an HNN group if it can be expressed as an HNN extension of some base.

The base group G embeds in the HNN extension in the obvious manner.

Theorem 9.9.16. Let G* be an HNN extension of base G. Then G is embedded in G* by g → g, that is the subgroup of G* generated by the generators of G, has the presentation (gens G; rels G). Further the free part {t,} is a basis for a free subgroup of G*.

As in all previous cases, this depends on a normal form for elements of HNN groups. However, this is somewhat more intricate than that for free products with amalgamation.

Suppose that G* is an HNN extension of G with associated subgroups {A,, f_j(A_j)} and suppose we choose a fixed set of left coset representatives for A, and f_j(A_j) in G where all A_i and f_i(A_i) are represented by 1. Then a normal form in G^* is a sequence

where g₁,... ,g_k+1 are elements of G such that for j < k if ej = 1 then gj is a left coset representative for A, in G while if ej = −1 then gj is a left coset representative for f_j(A_j) in G and ej = e_j+1 whenever g_j+1 = 1 and ij = i_j+1.

Theorem 9.9.17. Every element w in G* has a unique representation as a normal form.

From this as before we obtain a classification of torsion elements as well as a classification of abelian subgroups.

Theorem 9.9.18. Let G* be an HNN extension ofG.

(1)  Elements of finite order in G* are conjugate to elements of finite order in the base G. Further finite subgroups must be contained in conjugates of the base.

(2)  An abelian subgroup H ofG* is one of the following:

(a)  A subgroup of a conjugate of the base.

(b)  A countable ascending union of subgroups of conjugates of the associated subgroups.

(c)  An HNN group with presentation (t’, H’; relsH’, t’^H’f = H”) withH” c H’ and H’ is the intersection of the abelian subgroup H with finitely many conjugates of the associated subgroups.

We note that it is possible for a group to be both an HNN group and a free product with amalgamation. Consider the group

Let G₁ = (a, t; a² = (at)³ = 1). This is a free product of a cyclic group of order 2 generated by a and a cyclic group of order 3 generated by at. Therefore t has infinite order in G. Further let G₂ = (t, u; [t, u] = 1) a free abelian group of rank 2. The identification t → t is then an isomorphism and G is a free product of G₁ and G₂ with the infinite cyclic subgroup generated by t amalgamated.

Now write G as (u, a, t; a² = (at)³ = 1, u⁻¹tu = t). Again let G₁ = (a, t; a² = (at)³ = 1) = ₂ * ₃. Then G is an HNN extension of G₁ with the single pair of associated subgroups (t) and (f (t)) where f (t) = t.

We note that the above presentation is a presentation for the groups PE₂(O_d), the two dimensional projective elementary matrix group with entries in O_d, where O_d is the ring of integers in the quadratic imaginary number field Q(V-d) and d = 1, 2,3,7,11 (see [Fin]).

HNN groups were originally developed by G. Higman, H. Neumann and B. Neumann (whence the name) in order to prove several important embedding theorems. In particular:

Theorem 9.9.1. (see [Rot]). Every countable group can be embedded in a two generator group.

The concept and theory of of SQ-universality developed from this theorem.

Definition 9.9.20. A group G is SQ-universal if every countable group can be embedded isomorphically as a subgroup of a quotient of G.

Thus the Higman, Neumann, Neumann theorem above says that a free group of rank 2 is SQ-universal. Many linear groups as well as groups arising from low-dimensional topology are SQ-universal. SQ-universality might be thought of as a measure of “largeness” of an infinite group.

As mentioned at the beginning of this section, amalgam structures have a geometric-topological interpretation. We refer to [LS], [Ser], and [CRR] for an explanation of these.

9.10 Exercises

9.1    (a)  Let G be a group and H c G. Prove that H is a subgroup of G if and only if

(1)  H = 0,

(2)  H is closed with respect to the operation in G and inverses, that is, if a, b e H then ab e H and a⁻¹, b⁻¹ e H.

(b)  Let G be a group and H c G and assume H is non-empty. Prove that H is a subgroup of G if and only if a, b e H then ab⁻¹ e H. (This is sometimes called the one-step subgroup test.)

(c)  Show that the set of even integers forms a subgroup under addition of the additive group of Z.

9.2    (a)  Let R bea ring and let U(R) denote the set of elements with multiplicative inverses, that is, the set of units in R. Prove that U(R) forms a group. This is called the unit group of R.

(b)  If R is a field what is U(R)?

9.3    If F is a field show that the n x n matrices of non-zero determinant, GL(n, F), form a group and that SL(n, F), those matrices of determinant 1, is a normal subgroup.

9.4    Let G be a group and let a e G. Let

Sometimes we omit the subscript G and just write C(a). Prove that C(a) c G is a subgroup of G. This subgroup is called the centralizer of A in G.

9.5    Let G be a group and define

That is Z(G) is the set of elements in G that commute with every element of G. Prove that Z(G) forms a normal subgroup of G. This subgroup is called the center of G.

9.6    (a)  Show that the intersection of any non-empty collection of subgroups of a group G is a subgroup of G.

(b)  Show that if H, K are subgroups of G and the union H u K is also a subgroup of G then either H c K or K c H.

9.7    What are the generators of the additive group of the finite ring ₁₂?

9.8    Show that in S₃, the symmetric group on 3 symbols, we have (ab)² = 1 implies ab = ba².

9.9    Let G be a group and G’ be the subgroup of G generated by all commutators [a, b] = aba⁻¹b⁻¹. Show that this is a normal subgroup and the quotient group G/G’ is abelian.
The subgroup G’ is called the commutator subgroup of G, and the quotient G/G’ is called the abelianization of G.

9.10  (a)  Let F = (a, b;) be a free group of rank 2. Show, using the Reidemeister- Schreier procedure, that the commutator subgroup F’ is free of infinite rank.

(b)  Let F_n denote a free group of rank n and F_w denote a free group of countably infinite rank. Show that part (a) implies the following “snake eating its tail” situation where 2 < n < m <to;

9.11  Prove the following things about a free group (you may assume finite rank):

(a)  A free group is torsion-free that is every non-trivial element has infinite order.

(b)  Two non-trivial elements commute only if they both are powers of a single element. (Hint: use induction on the word lengths.)

(c)  Suppose W₁, W₂ are two words in the generators of F and their inverses. Then, if W₁ is a cyclic permutation of W₂, they represent conjugate elements.

9.12  Let M = PSL(2, Z) be the modular group. We saw that

(a)  Let M’ be the commutator subgroup of M. Show that M’ is free of rank 2. Hint: Use the Reidemeister-Schreier procedure. The abelianization of M is cyclic of order 6, and you can use as coset representatives (xy)^! where i = 0,1,2,3,4,5.

(b)  Explain why part (a) shows that within M there are free groups of every possible countable rank. This becomes important for certain cryptographic applications.

9.13  Let G = A * B be the free product of two groups A and B. Show that if two elements g, h e G commute then either they are both powers of a single element or both are in the same conjugate subgroup of one of the factors.
Hint: Use induction on the syllable length.