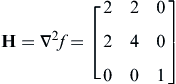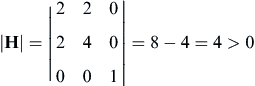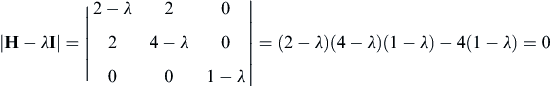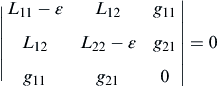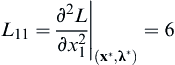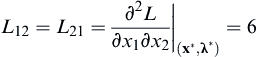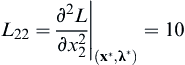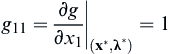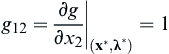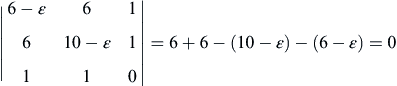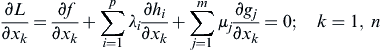3.3. Optimality Conditions
A basic knowledge of optimality conditions is important for understanding the performance of the various numerical methods discussed later in the chapter. In this section, we introduce the basic concept of optimality, the necessary and sufficient conditions for the relative maxima and minima of a function, as well as the solution methods based on the optimality conditions. Simple examples are used to explain the underlying concepts. The examples will also show the practical limitations of the methods.
3.3.1. Basic Concept of Optimality
We start by recalling a few basic concepts we learned in Calculus regarding maxima and minima, followed by defining local and global optima; thereafter, we illustrate the concepts using functions of one and multiple variables.
3.3.1.1. Functions of a single variable
This section presents a few definitions for basic terms.
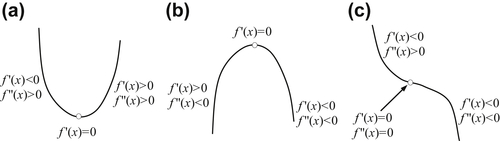
Stationary point: For a continuous and differentiable function f(x), a stationary point x∗ is a point at which the slope of the function vanishes—that is, f ′(x) = df/dx = 0 at x = x∗, where x∗ belongs to its domain of definition. As illustrated in Figure 3.7, a stationary point can be a minimum if f ″(x) > 0, a maximum if f ″(x) < 0, or an inflection point if f ″(x) = 0 in the neighborhood of x∗.
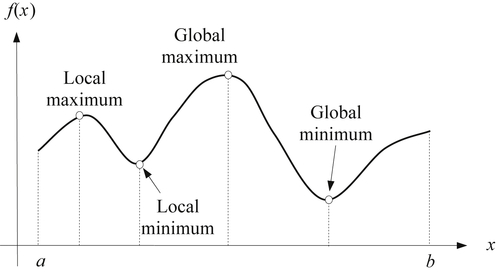
Global and local minimum: A function f(x) is said to have a local (or relative) minimum at x = x∗ if f(x∗) ≤ f(x∗ + δ) for all sufficiently small positive and negative values of δ, that is, in the neighborhood of the point x∗. A function f(x) is said to have a global (or absolute) minimum at x = x∗ if f(x∗) ≤ f(x) for all x in the domain over which f(x) is defined. Figure 3.8 shows the global and local optimum points of a function f(x) with a single variable x.
Necessary condition: Consider a function f(x) of single variable defined for a < x < b. To find a point of x∗∈(a, b) that minimizes f(x), the first derivative of function f(x) with respect to x at x = x∗ must be a stationary point; that is, f ′(x∗) = 0.
Sufficient condition: For the same function f(x) stated above and f ′(x∗) = 0, then it can be said that f(x∗) is a minimum value of f(x) if f ″(x∗) > 0, or a maximum value if f ″(x∗) < 0.
The concept illustrated above can be easily extended to functions of multiple variables. We use functions of two variables to provide a graphical illustration on the concepts.
3.3.1.2. Functions of multiple variables
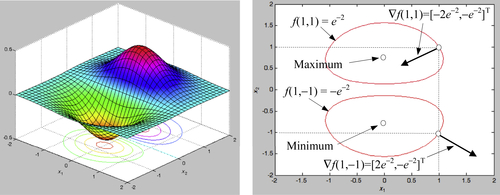
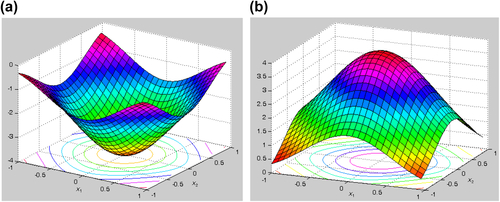
A function of two variables f(x1, x2) = −(cos2x1 + cos2x2)2 is graphed in Figure 3.9a. Perturbations from point (x1, x2) = (0, 0), which is a local minimum, in any direction result in an increase in the function value of f(x); that is, the slopes of the function with respect to x1 and x2 are zero at this point of local minimum. Similarly, a function f(x1, x2) = (cos2x1 + cos2x2)2 graphed in Figure 3.9b has a local maximum at (x1, x2) = (0, 0). Perturbations from this point in any direction result in a decrease in the function value of f(x); that is, the slopes of the function with respect to x1 and x2 are zero at this point of local maximum. The first derivatives of the function with respect to the variables are zero at the minimum or maximum, which again is called a stationary point.
Necessary condition: Consider a function f(x) of multivariables defined for x ∈ Rn, where n is the number of variables. To find a point of x∗ ∈ Rn that minimizes f(x), the gradient of the function f(x) at x = x∗ must be a stationary point; that is, ∇f(x∗) = 0.
The gradient of a function of multivariables is defined as
![]() (3.8)
(3.8)
Geometrically, the gradient vector is normal to the tangent plane at a given point x, and it points in the direction of maximum increase in the function. These properties are quite important; they will be used in developing optimality conditions and numerical methods for optimum design. In Example 3.2, the gradient vector for a function of two variables is calculated for illustration purpose.
Sufficient condition: For the same function f(x) stated above, let ∇f(x∗) = 0, then f(x∗) has a minimum value of f(x) if its Hessian matrix defined in Eq. 3.10 is positive-definite.
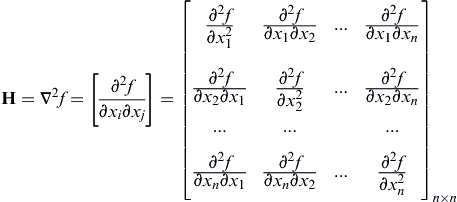 (3.10)
(3.10)
where all derivatives are calculated at the given point x∗. The Hessian matrix is an n × n matrix, where n is the number of variables. It is important to note that each element of the Hessian is a function in itself that is evaluated at the given point x∗. Also, because f(x) is assumed to be twice continuously differentiable, the cross partial derivatives are equal; that is,
![]() (3.11)
(3.11)
Therefore, the Hessian is always a symmetric matrix. The Hessian matrix plays a prominent role in exploring the sufficiency conditions for optimality.
Note that a square matrix is positive-definite if (a) the determinant of the Hessian matrix is positive (i.e., |H| > 0) or (b) all its eigenvalues are positive. To calculate the eigenvalues λ of a square matrix, the following equation is solved:
![]() (3.12)
(3.12)
where I is an identity matrix of n × n.
3.3.2. Basic Concept of Design Optimization
For an optimization problem defined in Eq. 3.3, we find design variable vector x to minimize an objective function f(x) subject to the inequality constraints gi(x) ≤ 0, i = 1 to m, the equality constraints hj(x) = 0, j = 1 to p, and the side constraints xkℓ ≤ xk ≤ xku, k = 1, n. In Eq. 3.5, we define the feasible set S, or feasible region, for a design problem as a collection of feasible designs. For unconstrained problems, the entire design space is feasible because there are no constraints. In general, the optimization problem is to find a point in the feasible region that gives a minimum value to the objective function. From a design perspective, in particular solving Eq. 3.3, we state the followings terms.
Global minimum: A function f(x) of n design variables has a global minimum at x∗ if the value of the function at x∗ ∈ S is less than or equal to the value of the function at any other point x in the feasible set S. That is,
![]() (3.14)
(3.14)
If strict inequality holds for all x other than x∗ in Eq. 3.14, then x∗ is called a strong (strict) global minimum; otherwise, it is called a weak global minimum.
Local minimum: A function f(x) of n design variables has a local (or relative) minimum at x∗ ∈ S if inequality of Eq. 3.14 holds for all x in a small neighborhood N (vicinity) of x∗. If strict inequality holds, then x∗ is called a strong (strict) local minimum; otherwise, it is called a weak local minimum.
Neighborhood N of point x∗ is defined as the set of points:
![]() (3.15)
(3.15)
for some small δ > 0. Geometrically, it is a small feasible region around point x∗, such as a sphere of radius δ for n = 3 (number of design variables n = 3).
Next, we illustrate the derivation of the necessary and sufficient conditions using Taylor's series expansion. For the time being, we assume unconstrained problems. In the next subsection, we extend the discussion to constrained problems.
Expanding the objective function f(x) at the inflection point x∗ using Taylor's series, we have
![]() (3.16)
(3.16)
where R is the remainder containing higher-order terms in Δx, and Δx = x − x∗. We define increment Δf(x) as
![]() (3.17)
(3.17)
If we assume a local minimum at x∗, then Δf must be nonnegative due to the definition of a local minimum given in Eq. 3.14; that is, Δf ≥ 0.
Because Δx is small, the first-order term ∇f(x∗)T Δx dominates other terms, and therefore Δf can be approximated as Δf(x) = ∇f(x∗)TΔx. Note that Δf in this equation can be positive or negative depending on the sign of the term ∇f(x∗)TΔx. Because Δx is arbitrary (a small increment in x∗), its components may be positive or negative. Therefore, we observe that Δf can be nonnegative for all possible Δx unless
![]() (3.18)
(3.18)
In other words, the gradient of the function at x∗ must be zero. In the component form, this necessary condition becomes
![]() (3.19)
(3.19)
Considering the second term on the right-hand side of Eq. 3.17 evaluated at a stationary point x∗, the positivity of Δf is assured if
![]() (3.20)
(3.20)
for all Δx ≠ 0. This is true if the Hessian H(x∗) is a positive-definite matrix, which is then the sufficient condition for a local minimum of f(x) at x∗.
3.3.3. Lagrange Multipliers
We begin the discussion of optimality conditions for constrained problems by including only the equality constraints in the formulation in this section; that is, inequalities in Eq. 3.3b are ignored temporarily. More specifically, the optimization problem is restated as
![]() (3.21a)
(3.21a)
![]() (3.21b)
(3.21b)
![]() (3.21c)
(3.21c)
The reason is that the nature of equality constraints is quite different from that of inequality constraints. Equality constraints are always active for any feasible design, whereas an inequality constraint may not be active at a feasible point. This changes the nature of the necessary conditions for the problem when inequalities are included.
A common approach for dealing with equality constraints is to introduce scalar multipliers associated with each constraint, called Lagrange multipliers. These multipliers play a prominent role in optimization theory as well as in numerical methods, in which a constrained problem is converted into an unconstrained problem that can be solved by using optimality conditions or numerical algorithms specifically developed for them. The values of the multipliers depend on the form of the objective and constraint functions. If these functions change, the values of the Lagrange multipliers also change.
Through Lagrange multipliers, the constrained problem (with equality constraints) shown in Eq. 3.21 is converted into an unconstrained problem as
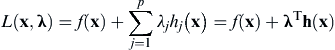 (3.22)
(3.22)
which is called a Lagrangian function, or simply Lagrangian. If we expand the vector of design variables to include the Lagrange multipliers, then the necessary and sufficient conditions of a local minimum discussed in the previous subsection are applicable to the problem defined in Eq. 3.22.
Before discussing the optimality conditions, we defined an important term called regular point. Consider the constrained optimization problem defined in Eq. 3.21, a point x∗ satisfying the constraint functions h(x∗) = 0 is said to be a regular point of the feasible set if the objective f(x∗) is differentiable and gradient vectors of all constraints at the point x∗ are linearly independent. Linear independence means that no two gradients are parallel to each other, and no gradient can be expressed as a linear combination of the others. When inequality constraints are included in the problem definition, then for a point to be regular, gradients of all the active constraints must also be linearly independent.
The necessary condition (or Lagrange multiplier theorem) is stated next.
Consider the optimization problem defined in Eq. 3.21. Let x∗ be a regular point that is a local minimum for the problem. Then, there exist unique Lagrange multipliers λj∗, j = 1, p such that
![]() (3.23)
(3.23)
Differentiating the Lagrangian L(x, λ) with respect to λj, we recover the equality constraints as
![]() (3.24)
(3.24)
The gradient conditions of Eqs 3.23 and 3.24 show that the Lagrangian is stationary with respect to both x and λ. Therefore, it may be treated as an unconstrained function in the variables x and λ to determine the stationary points. Note that any point that does not satisfy the conditions cannot be a local minimum point. However, a point satisfying the conditions need not be a minimum point either. It is simply a candidate minimum point, which can actually be an inflection or maximum point.
The second-order necessary and sufficient conditions, similar to that of Eq. 3.20, in which the Hessian matrix includes terms of Lagrange multipliers, can distinguish between the minimum, maximum, and inflection points. More specifically, a sufficient condition for f(x) to have a local minimum at x∗ is that each root of the polynomial in ε, defined by the following determinant equation be positive:
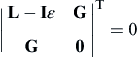 (3.25)
(3.25)
where
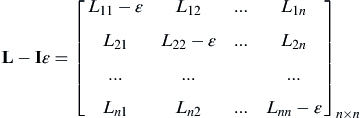 (3.26)
(3.26)
and
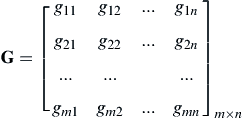 (3.27)
(3.27)
Note that Lij is a partial derivative of the Lagrangian L with respect to xi and λj, i.e., 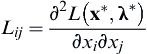 , i, j = 1, n; and gpq is the partial derivative of gp with respect to xq; i.e.,
, i, j = 1, n; and gpq is the partial derivative of gp with respect to xq; i.e., 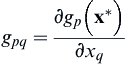 , p = 1, m and q = 1, n.
, p = 1, m and q = 1, n.
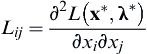 , i, j = 1, n; and gpq is the partial derivative of gp with respect to xq; i.e.,
, i, j = 1, n; and gpq is the partial derivative of gp with respect to xq; i.e., 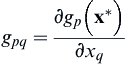 , p = 1, m and q = 1, n.
, p = 1, m and q = 1, n.3.3.4. Karush–Kuhn–Tucker Conditions
Next, we extend the Lagrange multiplier to include inequality constraints and consider the general optimization problem defined in Eq. 3.3.
We first transform an inequality constraint into an equality constraint by adding a new variable to it, called the slack variable. Because the constraint is of the form “≤”, its value is either negative or zero at a feasible point. Thus, the slack variable must always be nonnegative (i.e., positive or zero) to make the inequality an equality.
An inequality constraint gi(x) ≤ 0 is equivalent to the equality constraint
![]() (3.29)
(3.29)
where si is a slack variable. The variables si are treated as unknowns of the design problem along with the design variables. Their values are determined as a part of the solution. When the variable si has zero value, the corresponding inequality constraint is satisfied at equality. Such an inequality is called an active (or tight) constraint; that is, there is no “slack” in the constraint. For any si ≠ 0, the corresponding constraint is a strict inequality. It is called an inactive constraint, and has slack given by si2.
Note that once a design point is specified, Eq. 3.29 can be used to calculate the slack variable si2. If the constraint is satisfied at the point (i.e., gi(x) ≤ 0), then si2 ≥ 0. If it is violated, then si2 is negative, which is not acceptable; that is, the point is not a feasible point and hence is not a candidate minimum point.
Similar to that of Section 3.3.3, through Lagrange multipliers, the constrained problem (with equality and inequality constraints) defined in Eq. 3.3 is converted into an unconstrained problem as
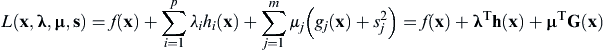 (3.30)
(3.30)
If we expand the vector of design variables to include the Lagrange multipliers λ and μ, and the slack variables s, then the necessary and sufficient conditions of a local minimum discussed in the previous subsection are applicable to the unconstrained problem defined in Eq. 3.30.
Note that derivatives of the Lagrangian L with respect to x and λ lead to Eqs 3.23 and 3.24, respectively. On the other hand, the derivatives of L with respect to μ yield converted equality constraints of Eq. 3.29. Furthermore, the derivatives of L with respect to s yield
![]() (3.31)
(3.31)
which is an additional necessary condition for the Lagrange multipliers of “≤ type” constraints given as
![]() (3.32)
(3.32)
where μj∗ is the Lagrange multiplier for the jth inequality constraint. Equations (3.32) is referred to as the nonnegativity of Lagrange multipliers (Arora 2012).
The necessary conditions for the constrained problem with equality and inequality constraints defined in Eq. 3.3 can be summed up in what are commonly known as the KKT first-order necessary conditions.
Karush–Kuhn–Tucker Necessary Conditions: Let x∗ be a regular point of the feasible set that is a local minimum for f(x), subject to hi(x) = 0; i = 1, p; gj(x) ≤ 0; j = 1, m. Then there exist Lagrange multipliers λ∗ (a p-vector) and μ∗ (an m-vector) such that the Lagrangian L is stationary with respect to xk, λi, μj, and sℓ at the point x∗; that is:
(2) Equality constraints:
![]() (3.34)
(3.34)
(3) Inequality constraints (or complementary slackness condition):
![]() (3.35)
(3.35)
![]() (3.36)
(3.36)
In addition, gradients of the active constraints must be linearly independent. In such a case, the Lagrange multipliers for the constraints are unique.
As seen in the example above, solving optimization problems using the KKT conditions is not straightforward, even for a simple problem. All possible cases must be identified and carefully examined. In addition, a sufficient condition that involves second derivatives of the Lagrangian is difficult to verify. Furthermore, for practical engineering design problems, objective and constraint functions are not expressed in terms of design variables explicitly, and taking derivatives analytically is not possible. After all, KKT conditions serve well for understanding the concept of optimality.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.