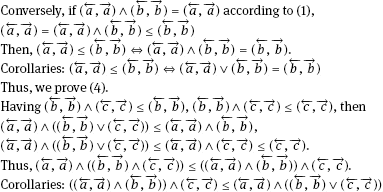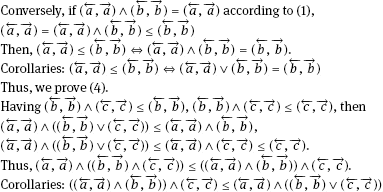
The prior of (5) is proved. The after is similar. Having

$\begin{array}{l}Having\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right),\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right),\text{then}\\ \left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right);\text{thus},\\ \left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)=\left(\overleftarrow{a},\overrightarrow{a}\right).\\ \text{Corollaries:}\left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\overleftarrow{b},\overrightarrow{b}\right)\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)\end{array}$

Definition 8.22 We call partial order set $\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)$ semilattice; when $\forall \left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right),$$\left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),\text{we}\text{have}\left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right)\vee \left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right)\text{or}\left(\overleftarrow{L},\overrightarrow{L}\right)\text{or}\left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right)\wedge \left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right).$

When $\forall \left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right),\left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),\text{we}\text{have}\left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right)\vee \left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),\left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right)\wedge$$\left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),$ then we call the partial order set $\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)$ as lattice.

Theorem 8.15 The necessary and sufficient conditions of set $\left(\overleftarrow{L},\overrightarrow{L}\right)$ are a lattice:

(1)There are two operations $\vee ,\wedge ,\text{for}\text{any}\left(\overleftarrow{a},\overrightarrow{a}\right),\left(\overleftarrow{b},\overrightarrow{b}\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),$ satisfying $\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge$
$\left(\overleftarrow{b},\overrightarrow{b}\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right).$

(2)$\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right),\left(\overleftarrow{b},\overrightarrow{b}\right)\wedge \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right)$ (Commutative law)

(3)$\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\right)$
$\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)\right)=\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)$ (Associative law)

(4)$\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)$
$\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right)\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)$ (Absorption law)

Proof: (sufficient)

(1): By known, we have $\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)$ is lattice, according the definition of lattice. We prove (1).

(2): Assume $\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{b},\overrightarrow{b}\right),\text{then}\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)$$\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right);$ in the same way, $\left(\overleftarrow{b},\overrightarrow{b}\right)\wedge \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge$$\left(\overleftarrow{b},\overrightarrow{b}\right).$

When $\left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right),$ in the same way, we can prove (2).

(3)(4):Corollaries, according to the method in (2) (necessary):

(1)For any $\left(\overleftarrow{a},\overrightarrow{a}\right),\left(\overleftarrow{b},\overrightarrow{b}\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),$ Then,
$\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right)\Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right).$
According to (2), $\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right)\Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right),$
Then, set $\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)$ is antisymmetry.

(2)Assume $\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{b},\overrightarrow{b}\right)\mathrm{and}\left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right).\text{Then,}$
$\begin{array}{l}\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{b},\overrightarrow{b}\right)\Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\\ \left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right)\Rightarrow \left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)\\ \text{According}\text{to}\left(2\right),\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{a},\overrightarrow{a}\right)\Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right).\\ \text{Then, set}\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)\text{is}\text{antisymmetry}\text{.}\end{array}$

(3)Assume $\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{b},\overrightarrow{b}\right),\left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{c},\overrightarrow{c}\right).\text{Then,}$
$\begin{array}{l}\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{c},\overrightarrow{c}\right)\\ \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\right)=\left(\overleftarrow{a},\overleftarrow{a}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\\ \text{According}\text{to}\left(3\right)\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\right)\\ \Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{c},\overrightarrow{c}\right)\Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{c},\overrightarrow{c}\right)\\ \text{Namely}\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(b,b\right),\left(b,b\right)\le \left(\overleftarrow{c},\overrightarrow{c}\right)\Rightarrow \left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{c},\overrightarrow{c}\right),\\ \text{Then,}\text{set}\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)\text{is}\text{transitive}\text{.}\end{array}$

(4)According to (1), for any $\left(\overleftarrow{a},\overrightarrow{a}\right),\left(\overleftarrow{b},\overrightarrow{b}\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),$ there are $\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right)\in$$\left(\overleftarrow{L},\overrightarrow{L}\right),\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right).$ Namely, the maximum lower bound and the minimum upper bound of any two elements are in the set. By (1)–(4), we can know that set $\left(\overleftarrow{L},\overrightarrow{L}\right)$ is lattice.
According to the necessary and sufficient condition, the theorem holds.

(Prove up).

Theorem 8.16 Assume $\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)$ is lattice, then we have the following properties:

$\begin{array}{l}\left(1\right)\left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overrightarrow{c},\overleftarrow{c}\right)=\left(\overleftarrow{a},\overleftarrow{a}\right)\Lambda \left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{a},\overleftarrow{a}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\\ \left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overrightarrow{c},\overleftarrow{c}\right)=\left(\overleftarrow{a},\overleftarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{a},\overleftarrow{a}\right)\vee \left(\overrightarrow{c},\overleftarrow{c}\right)\\ \left(2\right)\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\le \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\Lambda \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overrightarrow{c},\overleftarrow{c}\right)\right)\\ \left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\overleftarrow{b},\overrightarrow{b}\right)\vee \left(\overrightarrow{c},\overleftarrow{c}\right)\ge \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\vee \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\right)\end{array}$

$\begin{array}{l}\left(3\right)\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overrightarrow{c},\overleftarrow{c}\right)\iff \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\right)\\ \iff \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\right)\ge \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\Lambda \left(\overrightarrow{c},\overleftarrow{c}\right)\right)\end{array}$

Proof: (1) By Theorem 8.14: $\left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{c},\overrightarrow{c}\right)\iff \left(\overleftarrow{b},\overrightarrow{b}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{b},\overrightarrow{b}\right),$ then $\begin{array}{l}\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\wedge \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)\right)=\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{a},\overrightarrow{a}\right)\right)\wedge \left(\left(\overleftarrow{b},\overrightarrow{b}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)\right)=\\ \left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right),\text{thus}\left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{b},\overrightarrow{b}\right)\le \left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right).\end{array}$
Corollaries: $\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\le \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\right)$

(2)Hence, $\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\wedge \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\right)\text{and}\left(\left(\overleftarrow{b},\overrightarrow{b}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)\right)\le$$\left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{b},\overrightarrow{b}\right)\right)\wedge \left(\left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)\right);$ then the first part of (2) has been proved. In the same way, we can prove the second part.

(3)According to $\left(\overleftarrow{a},\overrightarrow{a}\right)\le \left(\overleftarrow{c},\overrightarrow{c}\right)\iff \left(\overleftarrow{a},\overrightarrow{a}\right)\vee \left(\overleftarrow{c},\overrightarrow{c}\right)=\left(\overleftarrow{c},\overrightarrow{c}\right)\iff \left(\overleftarrow{a},\overrightarrow{a}\right)\wedge \left(\overleftarrow{c},\overrightarrow{c}\right)$$\left(\overleftarrow{a},\overrightarrow{a}\right),$ namely (3).

[Prove up].

Definition 8.23 Lattice $\left(\left(\overleftarrow{L},\overrightarrow{L}\right),\le \right)$ is dense; when $\forall \left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right),\left(\overleftarrow{\beta },\overrightarrow{\beta }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right)$ and $\left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right)<\left(\overleftarrow{\beta },\overrightarrow{\beta }\right),$ there exists $\left(\overleftarrow{\gamma },\overrightarrow{\gamma }\right)\in \left(\overleftarrow{L},\overrightarrow{L}\right),\text{let}\text{satisfy}\left(\overleftarrow{\alpha },\overrightarrow{\alpha }\right)<\left(\overleftarrow{\gamma },\overrightarrow{\gamma }\right)<\left(\overleftarrow{\beta },\overrightarrow{\beta }\right).$