Chapter 3 Rate Laws

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

3. Rate Laws

Success is measured not so much by the position one has reached in life, as by the obstacles one has overcome while trying to succeed.

—Booker T. Washington

Overview. In Chapter 2, we showed that if we knew the rate of reaction as a function of conversion, – r_A = f(X), we could calculate reactor volumes necessary to achieve a specified conversion for flow systems and the time to achieve a given conversion in a batch system. Unfortunately, one is seldom, if ever, given – r_A = f(X) directly from raw data. Not to fear, in the next two chapters we will show how to obtain the rate of reaction as a function of conversion. This relationship between reaction rate and conversion will be obtained in two steps.

• In Step 1, described in this chapter, we define the rate law, which relates the rate of reaction to temperature and the concentrations of the reacting species.

• In Step 2, which will be described in Chapter 4, we define concentrations for flow and batch systems and develop stoichi-ometric tables that one can use to write concentrations as a function of conversion.

• Combining Steps 1 and 2, we see that one can then write the rate as a function of conversion, i.e., – r_A = f(X), and use the techniques in Chapter 2 to design reaction systems.

After completing this chapter, you will be able to

• relate the rates of reaction of species in a reaction to each other,

• write the rate law in terms of concentrations,

• use the Arrhenius Equation to find the rate constant as a function of temperature, and

• describe the energy barrier height (activation energy) and the fraction of molecular collisions that have the energy to pass over it and react.

3.1 Basic Definitions

Types of reactions

A homogeneous reaction is one that involves only one phase. A heterogeneous reaction involves more than one phase, and the reaction usually occurs at the interface between the phases. An irreversible reaction is one that proceeds in only one direction and continues in that direction until one of the reactants is Types ot reactions exhausted. A reversible reaction, on the other hand, can proceed in either direction, depending on the concentrations of reactants and products relative to the corresponding equilibrium concentrations. An irreversible reaction behaves as if no equilibrium condition exists. Strictly speaking, no chemical reaction is completely irreversible. However, for many reactions, the equilibrium point lies so far to the product side that these reactions are treated as irreversible reactions.

The molecularity of a reaction is the number of atoms, ions, or molecules involved (colliding) in a reaction step. The terms unimolecular, bimolecular, and termolecular refer to reactions involving, respectively, one, two, and three atoms (or molecules) interacting or colliding in any one reaction step. The most common example of a unimolecular reaction is radioactive decay, such as the spontaneous emission of an alpha particle from uranium-238 to give thorium and helium

U23892→Th234+He4290 ${}_{92}{U^{238}} \to {}_{90}{Th}^{234} + {}_{2}{He}^{4}$

The rate of disappearance of uranium (U) is given by the rate law

–r_U = kC_U

The only true bimolecular reactions are those that involve the collision with free radicals (i.e., unpaired electrons, e.g., Br•), such as

Br• + C₂H₆ → HBr + C₂H₅•

with the rate of disappearance of bromine given by the rate law

−rBr∙=kCBr∙CC2H6 $- r_{B r •} = k C_{Br •} C_{C_{2} H_{6}}$

The probability of a termolecular reaction, where three molecules collide all at once, is almost nonexistent, and in most instances the reaction pathway follows a series of bimolecular reactions, as in the case of the reaction

2NO + O2→2NO2 $2 NO + O_{2} \to 2 N O_{2}$

The reaction pathway for this “Hall of Fame” reaction is quite interesting and is discussed in Problem P9-5_A and in Web Chapter 16, along with similar reactions that form active intermediate complexes in their reaction pathways.

In discussing Rates of Chemical Reaction, we have three rates to consider

• Relative Rates

• Rate Laws

• Net Rates

Rehtive Rates tell us how fast one species is disappearing or appearing relative to the other species in the given reaction.

Rate Laws are the algebraic equations that give the rate of reaction as a function of the reacting species concentrations and of temperature in a specific reaction.

Reaction stoichiometry

Net Rates of formation of a given species (e.g., A) is the sum of the rate of reactions of A in all the reactions in which A is either a reactant or product in the system.

A thorough discussion of net rates is given in Table 8-2 where we discuss multiple reactions.

3.1.1 Relative Rates of Reaction

The relative rates of reaction of the various species involved in a reaction can be obtained from the ratio of the stoichiometric coefficients. For Reaction (2-2),

A+baB→caC+daD(2-2) $\begin{matrix} A+ \frac{b}{a} B \to \frac{c}{a} C+ \frac{d}{a} D & (2-2) \end{matrix}$

we see that for every mole of A that is consumed, c/a moles of C appear. In other words,

Rate of formation of C=ca×(Rate of disappearance of A) $Rate of formation of C = \frac{c}{a} \times (Rate of disappearance of A)$

rC=ca(−rA)=−carA $r_{C} = \frac{c}{a} (- r_{A}) = - \frac{c}{a} r_{A}$

Similarly, the relationship between the rates of formation of C and D is

rC=cdrD $r_{C} = \frac{c}{d} r_{D}$

The relationship can be expressed directly from the stoichiometry of the reaction

aA+bB→cC+dD(2-1) $\begin{matrix} a A + b B \to c C + d D & (2-1) \end{matrix}$

for which

−rAa=−rBb=rCc=rDd(3-1) $\begin{matrix} \frac{- r_{A}}{a} = \frac{- r_{B}}{b} = \frac{r_{C}}{c} = \frac{r_{D}}{d} & \begin{matrix} (3 -1) \end{matrix} \end{matrix}$

rA−a=rB−b=rCc=rDd $\begin{matrix} \frac{r_{A}}{- a} = \frac{r_{B}}{- b} = \frac{r_{C}}{c} = \frac{r_{D}}{d} \end{matrix}$

For example, in the reaction

2NO + O2⇄2NO2 $2 N O + O_{2} ⇄ 2 N O_{2}$

we have

rNO−2=rO2−1=rNO22 $\frac{r_{N O}}{- 2} = \frac{r_{O_{2}}}{- 1} = \frac{r_{N O_{2}}}{2}$

If NO₂ is being formed at a rate of 4 mol/m³/s, i.e.,

rNO2= 4 mol/m3/s $r_{N O_{2}} = 4 m o l / m^{3} / s$

then the rate of formation of NO is

rNO=−22rNO2=−4mol/m3/s $r_{N O} = \frac{- 2}{2} r_{N O_{2}} = - 4 m o l / m^{3} / s$

the rate of disappearance of NO is

−rNO = 4mol/m3/s $- r_{N O} = 4 m o l / m^{3} / s$

and the rate of disappearance of oxygen, O₂, is

−ro2 = −1−2rNO2 = 2mo1/m3/s $- r_{o_{2}} = \frac{- 1}{- 2} r_{N O_{2}} = 2 m o 1 / m^{3} / s$

Summary

2NO + O₂ → 2NO₂

rNO2 = 4mol/m3/s $r_{N O_{2}} = 4 m o l / m^{3} / s$

Then

−rNO = 4mol/m3/s $- r_{N O} = 4 m o l / m^{3} / s$

−rO2 = 2mol/m3/s $- r_{O_{2}} = 2 m o l / m^{3} / s$

3.2 The Rate Law

To understand the rate of reaction, we need to describe three molecular concepts. In Concept 1: Law of Mass Action, we use rate laws to relate the rate of reaction to the concentrations of the reacting species. Concept 2: Potential Energy Surfaces and Concept 3: The Energy Needed for Crossing the Barriers help us explain the effect of temperature on the rate of reaction.

In the chemical reactions considered in the following paragraphs, we take as the basis of calculation a species A, which is one of the reactants that is disappearing as a result of the reaction. The limiting reactant is usually chosen as our basis for calculation. The rate of disappearance of A, −r_A, depends on temperature and concentration. For many irreversible reactions, it can be written as the product of a reaction rate constant, k_A, and a function of the concentrations (activities) of the various species involved in the reaction:

−rA=[kA(T)][fn(CA,CB,...)](3−2) $\begin{matrix} - r_{A} = [k_{A} (T)] [fn (C_{A}, C_{B}, ...)] & (3 - 2) \end{matrix}$

Concept 1: Law of Mass Action. The rate of reaction increases with increasing concentration of reactants owing the corresponding increase in the number of molecular collisions. The rate law for bimolecular collisions is derived in the collision theory section of the Professional Reference Shelf R3.1 (http://www.umich.edu/~elements/5e/03chap/prof.html). A schematic of the reaction of A and B molecules colliding and reacting is shown in figure R3.1 on page 102.

The algebraic equation that relates −r_A to the species concentrations is called the kinetic expression or rate law. The specific rate of reaction (also called the rate constant), k_A, like the reaction rate, −r_A, always refers to a particular species in the reaction and normally should be subscripted with respect to that species. However, for reactions in which the stoichiometric coefficient is 1 for all species involved in the reaction, for example,

The rate law gives the relationship between reaction rate and concentration.

1 NaOH + 1 HC1 → 1 NaCl + 1 H₂O

we shall delete the subscript on the specific reaction rate, (e.g., A in k_A), to let

k=kNaOH=HHC1=kNaC1=kH2O $k = k_{N a O H} = H_{H C 1} = k_{N a C 1} = k_{H_{2} O}$

3.2.1 Power Law Models and Elementary Rate Laws

The dependence of the reaction rate, −r_A, on the concentrations of the species present, fn(C_j), is almost without exception determined by experimental observation. Although the functional dependence on concentration may be postulated from theory, experiments are necessary to confirm the proposed form. One of the most common general forms of this dependence is the power law model. Here the rate law is the product of concentrations of the individual reacting species, each of which is raised to a power, for example,

−rA=kACαACβB(3−3) $\begin{matrix} - r_{A} = k_{A} C_{A}^{α} C_{B}^{β} & (3 - 3) \end{matrix}$

Schematic shows a sheet of paper that reads, Rate Law with seven empty lines and at the bottom of the paper reads, plus 1HCL k subscript NAOH.

The exponents of the concentrations in Equation (3-3) lead to the concept of reaction order. The order of a reaction refers to the powers to which the concentrations are raised in the kinetic rate law¹ In Equation (3-3), the reaction is α order with respect to reactant A, and β order with respect to reactant B. The overall order of the reaction, n, is

¹ Strictly speaking, the reaction rates should be written in terms of the activities, a_i (a_i = γ_iC_i, where γ is the activity coefficient). Kline and Fogler, JCIS, 82, 93 (1981); ibid., p. 103; andind. Eng. Chem Fundamentals 20, 155 (1981).

- r A = k' A a α A a β B

$- r_{A} = k_{A}^{'} a_{A}^{α} a_{B}^{β}$

However, for many reacting systems, the activity coefficients, γ_i, do not change appreciably during the course of the reaction, and they are absorbed into the specific reaction rate constant, k_A

The equation under the elementary rate laws is shown.

The equation reads: Negative r subscript A equals k subscript A prime a subscript A (to the power of alpha) a subscript B (to the power of beta) equals k subscript A prime (gamma subscript A C subscript A) to the power of alpha (gamma subscript B C subscript B) to the power of beta equals (k subscript A prime gamma subscript A (to the power of alpha) gamma subscript B (to the power of beta) times C subscript A (to the power of alpha) C subscript B (to the power of beta) equals k subscript A C subscript A (to the power of alpha) C subscript B (to the power of beta). Since k subscript A prime gamma subscript A (to the power of alpha) gamma subscript B (to the power of beta) times C subscript A (to the power of alpha) C subscript B (to the power of beta) is collectively labeled "k subscript A."

−rA=k′AaαAaβB=k′A(γBCB)α(γBCB)β=(k′AγαAγβB)kACαACβB=kACαACβB $- r_{A} = k_{A}^{'} a_{A}^{α} a_{B}^{β} = k_{A}^{'} {(γ_{B} C_{B})}^{α} {(γ_{B} C_{B})}^{β} = \overset{k_{A}}{\overset{︷}{(k_{A}^{'} γ_{A}^{α} γ_{B}^{β})}} C_{A}^{α} C_{B}^{β} = k_{A} C_{A}^{α} {C_{B}^{β}}_{}$

n = α + β

Overall reaction

The units of –r_A order always in terms of concentration per unit time, while the units of the specific reaction rate, k_A, will vary with the order of the reaction. Consider a reaction involving only one reactant, such as

A → Products

with an overall reaction order n. The units of rate, –r_A, and the specific reaction rate, k are

{ –r_A } = [concentration/time]

and {k} = [concentration]1−ntime ${k} = \frac{[c o n c e n t r a t i o n]^{1 - n}}{t i m e}$

Generally, the overall reaction order can be deduced from the units of the specific reaction rate constant k. For example, the rate laws corresponding to a zero-, first-, second-, and third-order reaction, together with typical units for the corresponding rate constants, are

Zero-order(n=0):−rA=kA:{k}=mol/dm3/s(3-4) $\begin{matrix} Zero-order (n = 0) : & - r_{A} = k_{A} : \\ {k} = {mol/dm}^{3} / s & (3-4) \end{matrix}$

First-order(n=1):−rA=kACA:{k}=s−1(3-5) $\begin{matrix} First-order (n = 1) : & - r_{A} = k_{A} C_{A} : \\ {k} = s^{- 1} & (3-5) \end{matrix}$

Second-order(n=2):−rA=kAC2A:{k}=dm3/mol/s(3-6) $\begin{matrix} Second-order (n = 2) : & - r_{A} = k_{A} C_{A}^{2} : \\ {k} = {dm}^{3} / mol/s & (3-6) \end{matrix}$

Third-order(n=3):−rA=kAC3A:{k}=(dm3/mol)2/s(3-7) $\begin{matrix} Third-order (n = 3) : & - r_{A} = k_{A} C_{A}^{3} : \\ {k} = ({dm}^{3} / mol)^{2} / s & (3-7) \end{matrix}$

An elementary reaction is one that involves a single reaction step, such as the bimolecular reaction between an oxygen free radical and methanol molecule

O∙ + CH3OH→CH3O∙ + OH∙ ${O• + CH}_{3} OH \to {CH}_{3} O• + OH•$

The stoichiometric coefficients in this reaction are identical to the powers in the rate law. Consequently, the rate law for the disappearance of molecular oxygen is

−rO∙=kCO∙CCH3OH $- r_{O•} = k C_{O•} C_{{CH}_{3} OH}$

The reaction is first order in an oxygen free radical and first order in methanol; therefore, we say that both the reaction and the rate law are elementary. This form of the rate law can be derived from Collision Theory, as shown in the Professional Reference Shelf R3.1 on the CRE Web site (www.umich.edu/~elements/5e/index.html). There are many reactions where the stoichiometric coefficients in the reaction are identical to the reaction orders, but the reactions are not elementary, owing to such things as pathways involving active intermediates and series reactions. For these reactions that are not elementary but whose stoichiometric coefficients are identical to the reaction orders in the rate law, we say the reaction follows an elementary rate law. For example, the oxidation reaction of nitric oxide discussed earlier

Reference Shelf

2NO + O₂ → NO₂

Collision theory

is not really an elementary reaction, but follows an elementary rate law, i.e., second order in NO and first order in O₂, therefore,

−rNO=kNOC2NOCo2 $- r_{NO} {=k}_{NO} C_{NO}^{2} C_{o_{2}}$

Note: The rate constant, fe, is defined with respect to NO.

Another nonelementary reaction that follows an elementary rate law is the gas-phase reaction between hydrogen and iodine

H₂ + I₂ → 2HI

and is first order in H₂ and first order in I₂, with

−rH2=kH2CH2CI2 $- r_{H_{2}} = k_{H_{2}} C_{H_{2}} C_{I_{2}}$

In summary, for many reactions involving multiple steps and pathways, the powers in the rate laws surprisingly agree with the stoichiometric coefficients. Consequently, to facilitate describing this class of reactions, we say that a reaction follows an elementary rate law when the reaction orders are identical to the stoichiometric coefficients of the reacting species for the reaction as written. It is important to remember that the rate laws are determined by experimental observation! Chapter 7 describes how these and other rate laws can be developed from experimental data. They are a function of the reaction chemistry and not the type of reactor in which the reactions occur. Table 3-1 gives examples of rate laws for a number of reactions. By saying a reaction follows an elementary rate law as written gives us a quick way to look at the reaction stoichiometry and then write the mathematical form of the rate law. The values of specific reaction rates for these and a number of other reactions can be found in the Database found on the CRE Web site.

Where do you find rate laws?

The rate constants and the reaction orders for a large number of gas- and liquid-phase reactions can be found in the National Bureau of Standards’ circulars and supplements.² Also consult the journals listed at the end of Chapter 1.

² Kinetic data for a larger number of reactions can be obtained on CD−ROMs provided by National Institute of Standards and Technology (NIST). Standard Reference Data 221/A320 Gaithersburg, MD 20899; phone: (301) 975-2208. Additional sources are Tables of Chemical Kinetics: Homogeneous Reactions, National Bureau of Standards Circular 510 (Sept. 28, 1951); Suppl. 1 (Nov. 14, 1956); Suppl. 2 (Aug. 5, 1960); Suppl. 3 (Sept. 15,1961) (Washington, DC: U.S. Government Printing Office). Chemical Kinetics and Photochemical Data for Use in Stratospheric Modeling, Evaluate No. 10, JPL Publication 92-20 (Pasadena, CA: Jet Propulsion Laboratories, Aug. 15, 1992).

Where do you find rate laws?

We note in Table 3-1 that Reaction Number (3) in the First-Order Rate Laws and Reaction Number (1) in the Second-Order Rate Laws do not follow elementary reaction rate laws. We know this because the reaction orders are not the same as the stoichiometric coefficients for the reactions as they are written.^†

† Just as an aside, Prof. Dr. Sven Köttlov, a prominent resident of Rica, Jofostan, was once pulled over, questioned, and jailed for breaking a reaction rate law. He insisted that it was second order when experiments clearly showed it was first order.

Very important references. You should also look in the other literature before going to the lab.

TABLE 3-1 EXAMPLES OF REACTION RATE LAWS

Five examples of first-order rate laws are shown.

"In the first reaction, C subscript 2 H subscript 6 forms C subscript 2 H subscript 4 and hydrogen H subscript 2 with the rate of disappearance of A equals rate constant k times concentration of C subscript 2 H subscript 6.

In the second reaction, benzene ring single-bonded with N on the second carbon position which is double-bonded with NCl forms “benzene ring single-bonded with Cl on the second carbon position” and N subscript 2. The rate of disappearance of A equals constant k times concentration C of phi N double-bonded with NCl.

In the third reaction, two CH subscript 2 is single-bonded and in turn bonded to an oxygen atom in a cyclic manner and water (H subscript 2 O) reacts with sulphuric acid (H subscript 2 SO subscript 4) as a catalyst to form two single bonded CH subscript 2 OH. The rate of disappearance of CH subscript 2 OCH subscript 2 equals constant k times concentration of CH subscript 2 OCH subscript 2.

In the fourth reaction, CH subscript 3 COCH subscript 3 forms CH subscript 2 CO and CH subscript 4. The rate of disappearance of A equals constant k times concentration of CH subscript 3 COCH subscript 3.

In the fifth reaction, n C subscript 4 H subscript 10 involves in a reversible reaction to form i C subscript 4 H subscript 10. The rate of disappearance of n equals constant k [concentration of nC subscript 4 minus concentration of iC subscript 4 / K subscript C]."

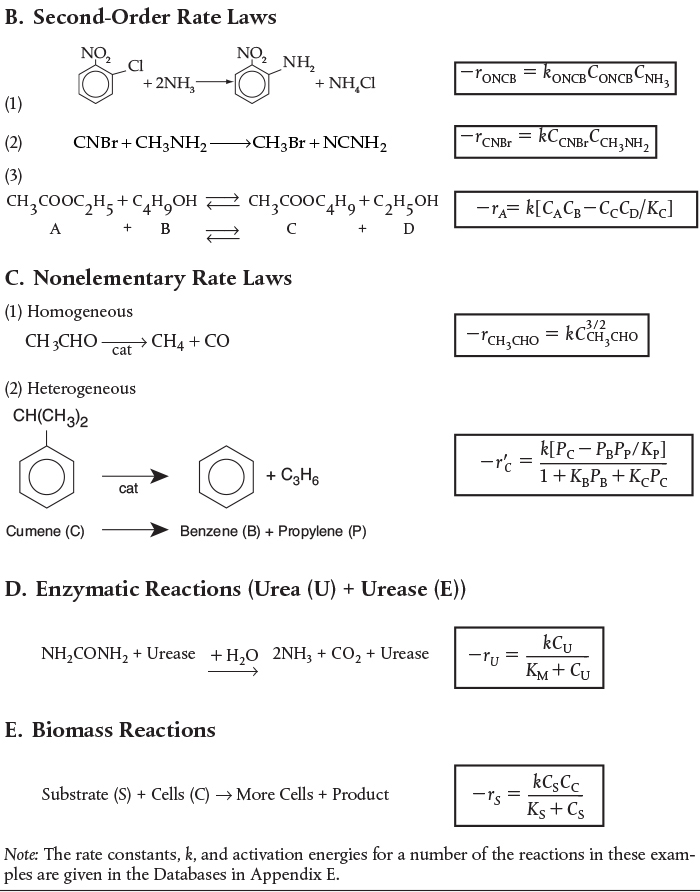
Examples of second-order rate laws, nonelementary rate laws, enzymatic reactions, and biomass reactions are shown.

"Three examples of second-order rate laws are shown. In the first reaction, benzene ring single-bonded with nitrogen dioxide (NO subscript 2) and chlorine (Cl) on the first and second carbon position reacts with two molecules of ammonia (NH subscript 3) to form benzene ring single-bonded with nitrogen dioxide (NO subscript 2) and amidogen (NH subscript 2) on the first and second carbon position and ammonium chloride (NH subscript 4 Cl). Rate of disappearance of ONCB equals rate constant k of ONCB times concentration C of ONCB times concentration C of ammonia (NH subscript 3). In the second reaction, CNBr reacts with CH subscript 3 NH subscript 2 to form CH subscript 3 Br and NCNH subscript 2. The rate of disappearance of CNBr equals constant k times concentration C of CNBr times concentration C of CH subscript 3 NH subscript 2. In the third reversible reaction, CH subscript 3 COOC subscript 2 H subscript 5 (represented as A) reacts with C subscript 4 H subscript 9 OH (represented as B) to form CH subscript 3 COOC subscript 4 H subscript 9 (represented as C) and C subscript 2 H subscript 5 OH (represented as D). The rate of disappearance of A equals constant k [concentration C of A times concentration C of B minus concentration C of C times concentration C of D/K subscript C].

Two nonelementary rate laws are shown. In the first homogeneous reaction, CH subscript 3 CHO reacts with a catalyst to form CH subscript 4 and CO. The rate of disappearance of CH subscript 3 CHO equals constant k times concentration C of CH subscript 3 CHO to the power of 3 over 2. In the second heterogeneous reaction, cumene (C) (in the form of a benzene ring single-bonded with CH(CH subscript 3) subscript 2 on the first carbon position) reacts with a catalyst to form benzene (B) and propylene (P) (C subscript 3 H subscript 6). The rate of disappearance negative r prime subscript C equals constant k [P subscript C minus P subscript B times P subscript P over K subscript P] over 1 plus K subscript B times P subscript B plus K subscript C times P subscript C.

An example of enzymatic reactions (Urea (U) plus Urease (E)) is shown. NH subscript 2 CONH subscript 2 and Urease react with water (H subscript 2 O) as a catalyst to form two molecules of ammonia (NH subscript 3) plus carbon dioxide (CO subscript 2) plus Urease. The rate of disappearance of Urea equals constant k times concentration C of Urea over K subscript M plus concentration C of Urea.

An example of biomass reactions is shown. The substrate (S) reacts with cells (C) to form more cells and product. The rate of disappearance of S equals constant k times concentration C of S times concentration C of C over italic K subscript S plus concentration C of S.

The text at the bottom reads as “Note: The rate constants, k, and activation energies for a number of the reactions in these examples are given in the Databases in Appendix E.”"

3.2.2 Nonelementary Rate Laws

A large number of both homogeneous and heterogeneous reactions do not follow simple rate laws. Examples of reactions that don’t follow simple elementary rate laws are discussed below.

Homogeneous Reactions. The overall order of a reaction does not have to be an integer, nor does the order have to be an integer with respect to any individual component. As an example, consider the gas-phase synthesis of phosgene,

CO + C1₂ → COC1₂

in which the kinetic rate law is

−rCO=kCCOC3/2C12 $- r_{CO} = k C_{CO} C_{{C1}_{2}}^{3 / 2}$

This reaction is first order with respect to carbon monoxide, three-halves order with respect to chlorine, and five-halves order overall.

Sometimes reactions have complex rate expressions that cannot be separated into solely temperature-dependent and concentration-dependent portions. In the decomposition of nitrous oxide,

2N2O→2N2+O2 $2 N_{2} O \to 2 N_{2} + O_{2}$

the kinetic rate law is

−rN2o=kN2OCN2O1+k′Co2 $- r_{N_{2} o} = \frac{k_{N_{2} O} C_{N_{2} O}}{1 + k^{'} C_{o_{2}}}$

Both kN2O $k_{N_{2} O}$ and k’ are strongly temperature dependent. When a rate expression such as the one given above occurs, we cannot state an overall reaction order. Here, we can only speak of reaction orders under certain limiting conditions. For example, at very low concentrations of oxygen, the second term in the denominator would be negligible with respect to 1(1>>k'CO2) $1 (1 >> k' C_{O_{2}})$ , and the reaction would be “apparent” first order with respect to nitrous oxide and first order overall. However, if the concentration of oxygen were large enough so that the number 1 in the denominator were insignificant in comparison with the second term, k'CO2(k'CO2>>1) $k' C_{O_{2}} (k' C_{O_{2}} >> 1)$ , the apparent reaction order would be –1 with respect to oxygen and first order with respect to nitrous oxide, giving an overall apparent zero order. Rate expressions of this type are very common for liquid and gaseous reactions promoted by solid catalysts (see Chapter 10). They also occur in homogeneous reaction systems with reactive intermediates (see Chapter 9).

It is interesting to note that although the reaction orders often correspond to the stoichiometric coefficients, as evidenced for the reaction between hydrogen and iodine, just discussed to form HI, the rate expression for the reaction between hydrogen and another halogen, bromine, is quite complex. This nonelementary reaction

H2+Br2→2HBr $H_{2} + B r_{2} \to 2 H B r$

proceeds by a free−radical mechanism, and its reaction rate law is

- r B r 2 = k B r 2 C H 2 C 1 / 2 B r 2 k ' + C H B r / C B r 2 (3-8)

$\begin{matrix} - r_{B r_{2}} = \frac{k_{B r_{2}} C_{H_{2}} C_{B r_{2}}^{1 / 2}}{k^{'} + C_{H B r} / C_{B r_{2}}} & (3-8) \end{matrix}$

Apparent First-Order Reactions. Because the law of mass action in collision theory shows that two molecules must collide giving a second-order dependence on the rate, you are probably wondering how rate laws such as Equation (3-8) as well as the rate law for first-order reactions come about. An example of first-order reaction not involving radioactive decay is the decomposition of ethanol to form ethylene and hydrogen.

C2H6→C2H4+H2 $C_{2} H_{6} \to C_{2} H_{4} + H_{2}$

−rC2H6=kCC2H6 $- r_{C_{2} H_{6}} = k C_{C_{2} H_{6}}$

In terms of symbols

A→B+C $A \to B + C$

−rA=kCA $- r_{A} = k C_{A}$

Rate laws of this form usually involve a number of elementary reactions and at least one active intermediate. An active intermediate is a high-energy molecule that reacts virtually as fast as it is formed. As a result, it is present in very small concentrations. Active intermediates (e.g., A*) can be formed by collision or interaction with other molecules (M) such as inerts or reactants

A+M→k1A*+M $A + M \overset{k_{1}}{\to} A^{*} + M$

Here, the activation occurs when translational kinetic energy is transferred into energy stored in internal degrees of freedom, particularly vibrational degrees of freedom.³ An unstable molecule (i.e., active intermediate) is not formed solely as a consequence of the molecule moving at a high velocity (high-translational kinetic energy). The translational kinetic energy must be absorbed into the chemical bonds where high-amplitude oscillations will lead to bond ruptures, molecular rearrangement, and decomposition. In the absence of photochemical effects or similar phenomena, the transfer of translational energy to vibrational energy to produce an active intermediate can occur only as a consequence of molecular collision or interaction. Collision theory is discussed in the Professional Reference Shelf on the CRE Web site for Chapter 3.

³W. J. Moore, Physical Chemistry (Reading, MA: Longman Publishing Group, 1998).

As will be shown in Chapter 9, the mole A becomes activated to A* by collision with another molecule M. The activated molecule can become deactivated by collision with another molecule or the activated molecule can decompose to B and C.

A+M⇆k2k1A∗+M↓k3B+C $\begin{matrix} A+M ⇆_{k_{2}}^{k_{1}} A^{*} + M \\ ↓ k_{3} \\ B+C \end{matrix}$

Using this mechanism, we show in Equation (9-10) in Section 9.1.1 that at high concentrations of M, the rate law for this mechanism becomes

−rA=k1k3k2CA=kACA $- r_{A} = \frac{k_{1} k_{3}}{k_{2}} C_{A} = k_{A} C_{A}$

and at low concentration of M, the rate law becomes

- r A = k 1 k 3 C A C M k 2 C M + k 3 \approx k 3 C A C M

$- r_{A} = \frac{k_{1} k_{3} C_{A} C_{M}}{k_{2} C_{M} + k_{3}} \approx k_{3} C_{A} C_{M}$

In Chapter 9, we will discuss reaction mechanisms and pathways that lead to nonelementary rate laws, such as the rate of formation of HBr shown in Equation (3-8).

Heterogeneous Reactions. Historically, it has been the practice in many gas-solid catalyzed reactions to write the rate law in terms of partial pressures rather than concentrations. In heterogeneous catalysis it is the weight of catalyst that is important, rather than the reactor volume. Consequently, we use −r′A $- r_{A}^{'}$ in order to write the rate law in terms of (mol per kg of catalyst per time) in order to design PBRs. An example of a heterogeneous reaction and corresponding rate law is the hydrodemethylation of toluene (T) to form benzene (B) and methane (M) carried out over a solid catalyst

CH56CH3+H2→catCH66+CH4 $C {}_{6}H_{5} C H_{3} + H_{2} \underset{cat}{\to} C {}_{6}H_{6} + C H_{4}$

The rate of disappearance of toluene per mass of catalyst, −r^’_T, i.e., (mol/mass/time) follows Langmuir-Hinshelwood kinetics (discussed in Section 10.4.2), and the rate law was found experimentally to be

−r′T=k'PH2PT1+KBPB+KTPT $- r_{T}^{'} = \frac{k' P_{H_{2}} P_{T}}{1 + K_{B} P_{B} + K_{T} P_{T}}$

where the prime in −r′T $- r_{T}^{'}$ notes typical units are in per kilogram of catalyst (mol/kg-cat/s), P_T, PH2 $P_{H_{2}}$ , and P_B are partial pressures of toluene, hydrogen, and benzene in (kPa or atm), and K_B and K_T are the adsorption constants for benzene and toluene respectively, with units of kPa^-1 (or atm⁻¹). The specific reaction rate k has units of

{k'}=mol toluenekg−cat⋅s⋅kPa2 ${k'} = \frac{m o l t o l u e n e}{k g - c a t \cdot s \cdot k P a^{2}}$

You will find that almost all heterogeneous catalytic reactions will have a term such as (1 + K_AP_A + ... ) or (1 + K_AP_A + ... )² in the denominator of the rate law (cf. Chapter 10).

To express the rate of reaction in terms of concentration rather than partial pressure, we simply substitute for P_i using the ideal gas law

Pi=CiRT(3-9) $\begin{matrix} P_{i} = C_{i} R T \end{matrix} \begin{matrix} (3 -9) \end{matrix}$

The rate of reaction per unit weight (i.e., mass) catalyst, −r′A $- r_{A}^{'}$ (e.g., −r′T $- r_{T}^{'}$ ), and the rate of reaction per unit volume, —r_A, are related through the bulk density pt (mass of solid/volume) of the catalyst particles in the fluid media:

−rA=(ρb)(−r′A)molestime⋅volume=(massvolume)(molestime⋅mass) $\begin{matrix} \begin{matrix} - r_{A} = (ρ_{b}) (- r_{A}^{'}) \end{matrix} \\ \frac{moles}{time \cdot volume} = (\frac{mass}{volume}) (\frac{moles}{time \cdot mass}) \end{matrix}$

In fluidized catalytic beds, the bulk density, ρ_b, is normally a function of the volumetric flow rate through the bed.

Relating rate per unit volume and rate by per unit mass of catalyst

Consequently using the above equations for P_i and −r′T $- r_{T}^{'}$ we can write the rate law for the hydromethylation of toluene in terms of concentration and in (mole/dm³) and the rate, −r_T in terms of reactor volume, i.e.,

−rT=[ρbk′(RT)2]kCH2CT1+KBRTCB+KTRTCT(moldm3⋅S)[k]=(dm3mol⋅S) $\begin{matrix} - r_{T} = \frac{\overset{k}{\overset{︷}{[ρ_{b} k^{'} {(R T)}^{2}]}} C_{H_{2}} C_{T}}{1 + K_{B} R T C_{B} + K_{T} R T C_{T}} (\frac{mol}{{dm}^{3} \cdot S}) \\ [k] = (\frac{{dm}^{3}}{mol \cdot S}) \end{matrix}$

or as we will see in Equation (S4-14) in Chapter 4 leave it in terms of partial pressures.

Thermodynamic equilibrium relationship

In summary on reaction orders, they cannot be deduced from reaction stoichiometry Even though a number of reactions follow elementary rate laws, at least as many reactions do not. One must determine the reaction order from the literature or from experiments.

3.2.3 Reversible Reactions

All rate laws for reversible reactions must reduce to the thermodynamic relationship relating the reacting species concentrations at equilibrium. At equilibrium, the net rate of reaction is identically zero for all species (i.e., − r_A ≡ 0). That is, for the general reaction

a A + b B ⇄ c C + d D (2-1)

$\begin{matrix} a A + b B ⇄ c C + d D & (2-1) \end{matrix}$

the concentrations at equilibrium are related by the thermodynamic relationship for the equilibrium constant K_C (see Appendix C).

kc=CcCeCdDeCaAeCbBe $k_{c} = \frac{C_{C e}^{c} C_{D e}^{d}}{C_{A e}^{a} C_{B e}^{b}}$ (3-10)

The units of the thermodynamic equilibrium constant, K_C, are (mol/dm³)^{d + c – b – a}.

To illustrate how to write rate laws for reversible reactions, we will use the combination of two benzene molecules to form one molecule of hydrogen and one of diphenyl. In this discussion, we shall consider this gas-phase reaction to be elementary as written and reversible

2C6H6⇆k−BkBC12H10+H2 $2 C_{6} H_{6} ⇆_{k_{- B}}^{k_{B}} C_{12} H_{10} + H_{2}$

or, symbolically,

2B⇆k−BkBD+H2 $2 B ⇆_{k_{- B}}^{k_{B}} D + H_{2}$

The forward and reverse specific reaction rate constants, k_B and k_−B, respectively, will be defined with respect to benzene.

Benzene (B) is being depleted by the forward reaction

2C6H6→kBC12H10+H2 $2 C_{6} H_{6} \overset{k_{B}}{\to} C_{12} H_{10} + H_{2}$

in which the rate of disappearance of benzene is

- r B, forward = k B C 2 B

$- r_{B, forward} = k_{B} C_{B}^{2}$

If we multiply both sides of this equation by −1, we obtain the expression for the rate of formation of benzene for the forward reaction

r B, forward = - k B C 2 B (3-11)

$\begin{matrix} r_{B, forward} = - k_{B} C_{B}^{2} & (3-11) \end{matrix}$

The specific reaction rate constant, k_i, must be defined with respect to a particular species.

For the reverse reaction between diphenyl (D) and hydrogen (H₂ ),

C 12 H 10 + H 2 - \to k - B 2 C 6 H 6

$C_{12} H_{10} + H_{2} \overset{k_{- B}}{\to} 2 C_{6} H_{6}$

the rate of formation of benzene is given as

r B, reverse = k - B C D C H 2 (3-12)

$\begin{matrix} r_{B, reverse} = k_{- B} C_{D} C_{H_{2}} & (3-12) \end{matrix}$

Again, both the rate constants k_B and k_−B are defined with respect to benzene!!!

The net rate of formation of benzene is the sum of the rates of formation from the forward reaction [i.e., Equation (3-11)] and the reverse reaction [i.e., Equation (3-12)]

r B \equiv r B, net = r B, forward + r B, reverse r B = - k B C 2 B + k - B C D C H 2 (3-13)

$\begin{matrix} r_{B} \equiv r_{B, net} = r_{B, forward} + r_{B, reverse} \\ r_{B} = - k_{B} C_{B}^{2} + k_{- B} C_{D} C_{H_{2}} & (3-13) \end{matrix}$

Net rate

Multiplying both sides of Equation (3-13) by −1, and then factoring out fe_B, we obtain the rate law for the rate of disappearance of benzene, −r_B

- r B = k B C 2 B - k - B C D C H 2 = (C 2 B - k - B k B C D C H 2)

$- r_{B} = k_{B} C_{B}^{2} - k_{- B} C_{D} C_{H_{2}} = (C_{B}^{2} - \frac{k_{- B}}{k_{B}} C_{D} C_{H_{2}})$

Replacing the ratio of the reverse to forward rate law constants by the reciprocal of the concentration equilibrium constant, K_C, we obtain

−rB=kB(C2B−CDCH2KC)(3-14) $\begin{matrix} - r_{B} = k_{B} (C_{B}^{2} - \frac{C_{D} C_{H_{2}}}{K_{C}}) \end{matrix} \begin{matrix} (3-14) \end{matrix}$

where

k B k - B = K C = Concentration equilibrium constant

$\frac{k_{B}}{k_{- B}} = K_{C} = Concentration equilibrium constant$

The equilibrium constant decreases with increasing temperature for exothermic reactions and increases with increasing temperature for endothermic reactions.

Let’s write the rate of formation of diphenyl, r_D, in terms of the concentrations of hydrogen, H₂, diphenyl, D, and benzene, B. The rate of formation of diphenyl, r_D, must have the same functional dependence on the reacting species concentrations as does the rate of disappearance of benzene, −r_B. The rate of formation of diphenyl is

r D = k D (C 2 B - C D C H 2 K C) (3-15)

$\begin{matrix} r_{D} = k_{D} (C_{B}^{2} - \frac{C_{D} C_{H_{2}}}{K_{C}}) & (3-15) \end{matrix}$

Using the relationship given by Equation (3-1) for the general reaction

rA−a=rB−b=rCc=rDd(3-1) $\begin{matrix} \frac{r_{A}}{- a} = \frac{r_{B}}{- b} = \frac{r_{C}}{c} = \frac{r_{D}}{d} \end{matrix} \begin{matrix} (3-1) \end{matrix}$

Relative rates

we can obtain the relationship between the various specific reaction rates, k_B, k_D

r D 1 = r B - 2 = - k B [ C 2 B - C D C H 2 / K C ] - 2 = k B 2 [C 2 B - C D C H 2 K C] (3-16)

$\begin{matrix} \frac{r_{D}}{1} = \frac{r_{B}}{- 2} = \frac{- k_{B} [C_{B}^{2} - C_{D} C_{H_{2}} / K_{C}]}{- 2} = \frac{k_{B}}{2} [C_{B}^{2} - \frac{C_{D} C_{H_{2}}}{K_{C}}] & (3-16) \end{matrix}$

Comparing Equations (3-15) and (3-16), we see the relationship between the specific reaction rate with respect to diphenyl, k_D, and the specific reaction rate with respect to benzene, k_B, is

kD=kB2 $k_{D} = \frac{k_{B}}{2}$

Consequently, we see the need to define the rate constant, k, with respect to a particular species.

Finally, we need to check to see if the rate law given by Equation (3-14) is thermodynamically consistent at equilibrium. Applying Equation (3-10) (and Equation (C-2) in Appendix C) to the diphenyl reaction and substituting the appropriate species concentration and exponents, thermodynamics tells us that

K C = C De C H 2 e C 2 Be (3-17)

$\begin{matrix} K_{C} = \frac{C_{De} C_{H_{2}} e}{C_{Be}^{2}} & (3-17) \end{matrix}$

Now let’s look at the rate law. At equilibrium, –r_B ≡ 0, and the rate law given by Equation (3-14) becomes

- r B \equiv 0 = k B [C 2 B e - C De C H 2 e K C]

$- r_{B} \equiv 0 = k_{B} [C_{B e}^{2} - \frac{C_{De} C_{H_{2}} e}{K_{C}}]$

At equilibrium, the rate law must reduce to an equation consistent wth thermodynamic equilibrium.

Rearranging, we obtain, as expected, the equilibrium expression

KC=CDeCH2eC2Be $K_{C} = \frac{C_{De} C_{H_{2} e}}{C_{Be}^{2}}$

that is identical to Equation (3-17) obtained from thermodynamics.

From Appendix C, Equation (C-9), we know that when there is no change in the total number of moles and the heat capacity term, ΔC_P = 0, the temperature dependence of the concentration equilibrium constant is

KC(T)=KC(T1)exp[ΔH∘RxR(1T1−1T)](C-9) $\begin{matrix} K_{C} (T) = K_{C} (T_{1}) \exp [\frac{Δ H_{Rx}^{\circ}}{R} (\frac{1}{T_{1}} - \frac{1}{T})] \end{matrix} \begin{matrix} (C-9) \end{matrix}$

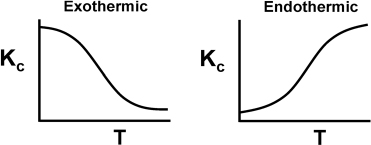
Graph shows two curves labeled Exothermic and Endothermic in which the horizontal axis represents "T" and the vertical axis represents "K subscript c."

Therefore, if we know the equilibrium constant at one temperature, T₁ [i.e., K_C (T₁], and the heat of reaction, ΔH∘Rx $Δ H_{Rx}^{\circ}$ , we can calculate the equilibrium constant at any other temperature T. For endothermic reactions, the equilibrium constant, K_C, increases with increasing temperature; for exothermic reactions, K_C decreases with increasing temperature. A further discussion of the equilibrium constant and its thermodynamic relationship is given in Appendix C. For large values of the equilibrium constant, K_C, the reaction behaves as if it were irreversible.

Arrhenius equation

3.3 The Reaction Rate Constant

In Section 3.2, we discussed Concept 1, the dependence of the reaction rate on concentration. In this section we investigate the reaction rate constant, k, and it’s temperature dependence using Concept 2, potential energy surfaces and energy barriers, and Concept 3, the energy needed to cross over these barriers.

3.3.1 The Rate Constant k and Its Temperature Dependence

The reaction rate constant k is not truly a constant; it is merely independent of the concentrations of the species involved in the reaction. The quantity k is referred to as either the specific reaction rate or the rate constant. It is almost always strongly dependent on temperature. It also depends on whether or not a catalyst is present, and in gas-phase reactions, it may be a function of total pressure. In liquid systems it can also be a function of other parameters, such as ionic strength and choice of solvent. These other variables normally exhibit much less effect on the specific reaction rate than does temperature, with the exception of supercritical solvents, such as supercritical water. Consequently, for the purposes of the material presented here, it will be assumed that k_A depends only on temperature. This assumption is valid in most laboratory and industrial reactions, and seems to work quite well.

It was the great Nobel Prize–winning Swedish chemist Svante Arrhenius (1859–1927) who first suggested that the temperature dependence of the specific reaction rate, k_A, could be correlated by an equation of the type

kA(T)=Ae−E/RT(3-18) $\begin{matrix} k_{A} (T) = A e^{- E / R T} & (3-18) \end{matrix}$

where

A = pre-exponential factor or frequency factor

E = activation energy, J/mol or cal/mol

R = gas constant = 8.314 J/mol · K = 1.987 cal/mol · K

T = absolute temperature, K

(http://www.umich.edu/~elements/5e/03chap/summary.html)

Graph shows a curve with horizontal axis represents T (in Kelvin) and vertical axis represents k. The curve starts from the origin and rises up gradually.

Reference Shelf

Equation (3-18), known as the Arrhenius equation, has been verified empirically to give the correct temperature behavior of most reaction rate constants within experimental accuracy over fairly large temperature ranges. The Arrhenius equation is derived in the Professional Reference Shelf R3.A: Collision Theory on the CRE Web site.

Additionally, one can view the activation energy in terms of collision theory (Professional Reference Shelf R3.1). By increasing the temperature, we increase the kinetic energy of the reactant molecules. This kinetic energy can in turn be transferred through molecular collisions to internal energy to increase the stretching and bending of the bonds, causing them to reach an activated state, vulnerable to bond breaking and reaction.

3.3.2 Interpretation of the Activation Energy

Why is there an activation energy? If the reactants are free radicals that essentially react immediately on collision, there usually isn’t an activation energy. However, for most atoms and molecules undergoing reaction, there is an activation energy. A couple of the reasons are that in order to react

1. The molecules need energy to distort or stretch their bonds so that they break and now can form new bonds.

2. The molecules need energy to overcome the steric and electron repulsive forces as they come close together.

The activation energy can be thought of as a barrier to energy transfer (from kinetic energy to potential energy) between reacting molecules that must be overcome. The activation energy is the minimum increase in potential energy of the reactants that must be provided to transform the reactants into products. This increase can be provided by the kinetic energy of the colliding molecules.

In addition to the concentrations of the reacting species, there are two other factors that affect the rate of reaction,

• the height of the potential energy barrier, i.e., activation energy, and

• the fraction of molecular collisions that have sufficient energy to cross over the barrier (i.e., react when the molecules collide).

If we have a small barrier height, the molecules colliding will need only low kinetic energies to cross over the barrier. For reactions of molecules with small barrier heights occurring at room temperatures, a greater fraction of molecules will have this energy at low temperatures. However, for larger barrier heights, we require higher temperatures where a higher fraction of colliding molecules will have the necessary energy to cross over the barrier and react. We will discuss each of these concepts separately.

Concept 2. Potential Energy Surfaces and Energy Barriers. One way to view the barrier to a reaction is through the use of potential energy surfaces and the reaction coordinates. These coordinates denote the minimum potential energy of the system as a function of the progress along the reaction path as we go from reactants to an intermediate to products. For the exothermic reaction

A+BC⇄A−B−C→AB+C $A + B C ⇄ A - B - C \to A B + C$

the potential energy surface and the reaction coordinate are shown in Figures 3-1 and 3-2. Here E_A, E_AB, E_BC, and E_c are the potential surface energies of the reactants (A and BC) and products (AB and C), while E_ABC is the energy of the complex A-B-C at the top of the barrier shown in Figure 3-2(a).

Figure 3-1 (a) shows a 3D plot of the potential energy surface, which is analogous to a mountain pass where we start out in a valley and then climb up to pass over the top of the pass, i.e., the col or saddle point, and proceed down into the next valley. Figure 3-1 (b) shows a contour plot of the pass and valleys and the reaction coordinate as we pass over the col from valley to valley.

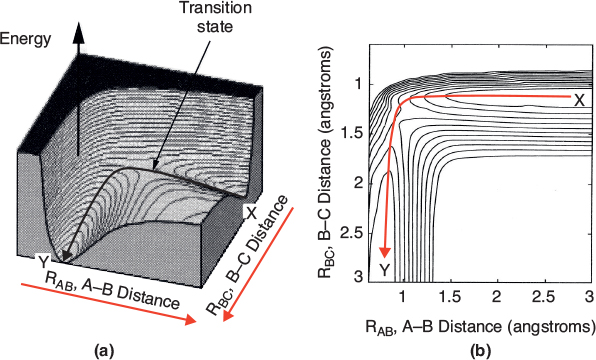
Two graphs, graph (a) and graph (b) are shown.

Figure 3-1 A potential energy surface for the H + CH₃OH→ H₂ + CH₂OH from the calculations of Blowers and Masel. The lines in the figure are contours of constant energy. The lines are spaced 5 kcal/mol. Richard I. Masel, Chemical Kinetics and Catalysis, p. 370, Fig. 7.6 (Wiley, 2001).

Progress along reaction path is shown in three graphs.

"In graph (a), the horizontal axis represents ""Reaction coordinate"" and the vertical axis represents ""Potential energy."" The left part of the horizontal axis represents ""reactants (X)"" and the right part represents ""products (Y)."" A curve starts from the mid of the vertical axis and decreases gradually up to a horizontal line representing ""E subscript A plus E subscript BC."" The trough of the curve, the reactants labeled ""A plus BC."" The curve then increases gradually up to a peak. The peak labeled ""A minus B minus C."" Pointers to and fro between A plus BC and A minus B minus C indicate that the process undergoes a reversible reaction. A horizontal line toward the peak represents ""E subscript A minus B minus C. The curve then decreases gradually up to a horizontal line at the bottom representing ""E subscript AB plus E subscript C."" The curve then increases again. The trough at right labeled ""AB plus C."" The distance between the bottom two horizontal lines E subscript A plus E subscript BC and E subscript AB plus E subscript C is labeled ""Delta H subscript RX,"" and the distance between the top two horizontal lines E subscript A minus B minus C and E subscript A plus E subscript BC is labeled ""E subscript B (Energy barrier).""

The reaction “methyl iodide (CH subscript 3 I) reacting with Chlorine (Cl) in a reversible reaction to form methyl chloride (CH subscript 3 Cl) and iodine (I)” is labeled above graph (b). The horizontal axis representing “CH subscript 3 - I Bond distance in angstroms” ranges from 1.9 to 2.7, in increments of 0.2, and the vertical axis representing “ground state energy” ranges from 41 to 23, in decrements of 2, with an exception being 39 decreasing to 36 and 36 decreasing to 33. A curve starts from 33 of the vertical axis and decreases gradually up to the left of 1.9 of the horizontal axis and then the curve increases again up to a peak. The curve then decreases again gradually and becomes stable between 27 and 29 of the vertical axis. The left part of the curve labeled ""Reactants,"" the middle part labeled ""Transition state,"" and the right part labeled ""Products.""

In graph (c), the horizontal axis represents ""R subscript BC (angstroms)"" and the vertical axis represents ""Energy (in kilocalories per mole)."" A U-shaped curve is drawn with a dot at the bottom of the curve labeled ""Equilibrium BC position."""

Figure 3-2 Progress along reaction path, (a) Symbolic reaction; (b) Calculated from computational software on the CRE Web site, Chapter 3 Web Module, (c) Side view at point X in Figure 3-1(b), showing the valley.

Energy changes as we move within the potential energy surfaces.

At point X in Figure 3-1 (b), species A and BC are far apart and are not interacting, and R_BC is just the equilibrium bond length between B and C. Consequently the potential energy is just the BC bond energy. Here, species A and BC are in their minimum potential energy in the valley and the steep rise up from the valley to the col from X would correspond to increases in the potential energy as A comes close to BC. Figure 3-2(c) illustrates when the BC bond is stretched from its equilibrium position at point X, the potential energy increases up one side of the valley hill (R_BC increases). The potential energy is now greater because of the attractive forces trying to bring the B-C distance back to its equilibrium position. If the BC bond is compressed at X from its equilibrium position, the repulsive forces cause the potential energy to increase on the other side of the valley hill, i.e., R_BC decreases at X. At the end of the reaction, point Y, the products AB and C are far apart on the valley floor and the potential energy is just the equilibrium AB bond energy. The sides of the valley at Y represent the cases where AB is either compressed or stretched causing the corresponding increases in potential energy at point Y and can be described in an analogous manner to BC at point X.

We want the minimum energy path across the barrier for converting the kinetic energy of the molecules into potential energy. This path is shown by the curve X→Y in Figure 3-1 and also by Figure 3-2(a). As we move along the A-B distance axis in Figure 3-2(a), A comes closer to BC and B begins to bond with A and to push BC apart such that the potential energy of the reaction pair continues to increase until we arrive at the top of the energy barrier, which is the transition state. In the transition state the molecular distances between A and B and between B and C are close. As a result, the potential energy of the three atoms (molecules) is high. As we proceed further along the arc length of the reaction coordinate depicted in Figure 3-1(a), the AB bond strengthens and the BC bond weakens and C moves away from AB and the energy of the reacting pair decreases until we arrive at the valley floor where AB is far apart from C. The reaction coordinate quantifies how far the reaction has progressed. The commercial software available to carry out calculations for the transition state for the real reaction

Reference Shelf

CH3I+Cl→CH3Cl+I ${CH}_{3} I+ Cl \to {CH}_{3} Cl+I$

shown in Figure 3-2(b) is discussed in the Web Module Molecular Modeling in Chemical Reaction Engineering on the CRE Web site.

We next discuss the pathway over the barrier shown along the line Y-X. We see that for the reaction to occur, the reactants must overcome the minimum energy barrier, E_B, shown in Figure 3-2(a). The energy barrier, E_B, is related to the activation energy, E. The energy barrier height, E_B, can be calculated from differences in the energies of formation of the transition-state molecule and the energy of formation of the reactants; that is,

Schematic shows a spider web connected to a mouse through a wire labeled Web Modules.

EB=E∘fA−B−C−(E∘fA+E∘fB−C) $E_{B} = E_{f A - B - C}^{\circ} - (E_{f A}^{\circ} + E_{f B - C}^{\circ})$

The energy of formation of the reactants can be found in the literature or calculated from quantum mechanics, while the energy of formation of the transition state can also be calculated from quantum mechanics using a number of software packages, such as Gaussian (http://www.gaussian.com/) and Dacapo (https://wiki.fysik.dtu.dk/dacapo). The activation energy, E, is often approximated by the barrier height, E_B, which is a good approximation in the absence of quantum mechanical tunneling.

Now that we have the general idea for a reaction coordinate, let’s consider another real reaction system

H• + C₂H₆ → H₂ + C₂H₅•

The energy−reaction coordinate diagram for the reaction between a hydrogen atom and an ethane molecule is shown in Figure 3-3 where the bond distortions, breaking, and forming are identified. This figure shows schematically how the hydrogen molecule, H, moves into CH₃–CH₃ molecule, distorting the C–H bond and pushing the C–H bond off the methyl hydrogen to arrive at the transition state. As one continues along the reaction coordinate, the methyl hydrogen moves out of the C–H bond into the H-H bond to form the products CH₃CH₂ and H₂.

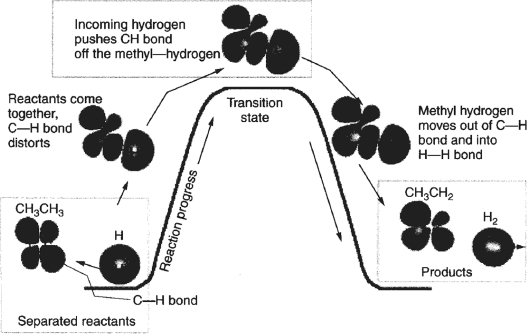
A diagram of the orbital distortions during a reaction is shown.

Figure 3-3 A diagram of the orbital distortions during the reaction H • + CH₃CH₃ → H₂ + CH₂CH₃ • The diagram shows only the interaction with the energy state of ethane (the C–H bond). Other molecular orbitals of the ethane also distort. Courtesy of Richard I. Masel, Chemical Kinetics and Catalysis, p. 594 (Wiley 2001).

Concept 3. Fraction of Molecular Collisions That Have Sufficient Energy to React. Now that we have established a barrier height, we need to know what fraction of molecular collisions have sufficient energy to cross over the barrier and react. To discuss this issue, we consider reactions in the gas phase where the reacting molecules will not have only a single velocity, U, but a distribution of velocities, f(U,T). Some will have high velocities and some will have low velocities as they move around and collide. These velocities are not defined with respect to a fixed coordinate system; these velocities are defined with respect to the other reactant molecules. The Maxwell-Boltzmann distribution of relative velocities is given by the probability function, f(U, T)

f (U, T)=4 π (m 2 π k B T) 3 / 2 exp [- m U 2 2 k B T] U 2

$f (U, T)=4 π {(\frac{m}{2 π k_{B} T})}^{3 / 2} \exp [\frac{- m U^{2}}{2 k_{B} T}] U^{2}$

k_B = Boltzmann’s constant = 3.29 X 10 ²⁴ cal/molecule/K

m = Reduced mass, g

U = Relative velocity, m/s

T = Absolute Temperature, K

e = Energy kcal/molecule

E = Kinetic energy kcal/mol

We usually interpret f(U, T) with dU, i.e., f(U, T) dU = fraction of reactant molecules with velocities between U and (U + dU).

Rather than using velocities to discuss the fraction of molecules with sufficient energy to cross the barrier, we convert these velocities to energies using the equation for kinetic energy in making this conversion

e = 1 2 m U 2

$e = \frac{1}{2} m U^{2}$

Using this substitute, the Maxwell Boltzmann probability distribution of collisions with energy e (cal/molecule) at temperature T is

f (e, T) = 2 π (1 π k B T) 3 / 2 e 1 / 2 exp [- e k B T] (3-19)

$\begin{matrix} f (e, T) = 2 π {(\frac{1}{π k_{B} T})}^{3 / 2} e^{1 / 2} \exp [\frac{- e}{k_{B} T}] & (3-19) \end{matrix}$

In terms of energy per mole, E, instead of energy per molecule, e, we have

f (E, T) = 2 π (1 π R T) 3 / 2 E 1 / 2 exp [- E R T] (3-20)

$\begin{matrix} f (E, T) = 2 π {(\frac{1}{π R T})}^{3 / 2} E^{1 / 2} \exp [\frac{- E}{R T}] & (3-20) \end{matrix}$

where E is in (cal/mol), R is in (cal/mol/K), and f(E, T) is in mol/cal.

This function is plotted for two different temperatures in Figure 3-4. The distribution function f(E,T) is most easily interpreted by recognizing that [f(E,T) dE] is the fraction of collision with energies between E and E + dE.

f (E, T) d E = 2 π (1 π k B T) 3 / 2 E 1 / 2 exp [- - E k B T] d E (3-21)

$\begin{matrix} f (E, T) d E = 2 π {(\frac{1}{π k_{B} T})}^{3 / 2} E^{1 / 2} \exp [- \frac{- E}{k_{B} T}] d E & (3-21) \end{matrix}$

For example, the fraction of collisions with energies between 0.25 kcal/mol and 0.35 kcal/mol would be

(Fraction with energies to between (0.25 and 0.35) kcal mol) = \int 0.35 0.25 f (E, T) d E

$(Fraction with energies to between (0.25 and 0.35) \frac{kcal}{mol}) = \int_{0.25}^{0.35} f (E, T) d E$

This fraction is shown by the shaded area in Figure 3-4 and is approximated by the average value of f(E,T) at E = 0.3 kcal/mole is 0.81 mol/kcal.

f (E, T) d E = f (0.3, 300 k) Δ E = 0.81 mol kcal (0.35 kcal mol - 0.25 kcal mol) = 0.081

$f (E, T) d E = f (0.3, 300 k) Δ E = \frac{0.81 mol}{kcal} (0.35 \frac{kcal}{mol} - 0.25 \frac{kcal}{mol}) = 0.081$

Graph shows two curves representing energy distribution of reacting molecules.

"The horizontal axis representing “E (in kilocalories per mole)” ranges from 0 to 6, in increments of 0.5 and the vertical axis representing “f (E, T) (in kilocalories per mole) inverse” ranges from 0 to 0.9, in increments of 0.1. A curve labeled T subscript 1 equals 300K starts from the origin, rises to the point (0.3, 0.81), slides, and then tends to approach the horizontal axis at the right. A curve labeled T subscript 2 equals 500K starts from the origin, rises to the point (0.35, 0.49), slides, and then tends to approach the horizontal axis at the right. Text pointing to a shaded vertical bar between (0.25, 0) and (0.35, 0) reads: The fraction of collisions with energies between 0.25 and 0.35 kilocalories per mole is approximately f(E,T)dE equals (0.81 kilocalories per mole)inverse times (0.1 kilocalories per mole) equals 0.081; that is, 8.1 percent of the molecular collisions have energies between 0.25 and 0.35 kcal/mol. Text pointing to the region enclosed by the curves near the right end and the vertical line at 2.5 reads: The fraction of collisions at T equals 500K that have energy EA of 2.5 kilocalories per mole or greater. Text to the right of the curves read: T subscript 2 is greater than T subscript 1."

Figure 3-4 Energy distribution of reacting molecules.

Thus 8.1% of the molecular collisions have energies between 0.25 and 0.35 kcal/mol. Go to the LEP “Energy Distribution” and use Wolfram to see how the distribution changes as the temperature changes. Wolfram can be downloaded on your laptop for free (go to http://www.wolfram.com/cdf-player/).

We can also determine the fraction of collision that have energies greater than a certain value, E_A

⎛ ⎝ ⎜ Fraction of Molecules with E > E A ⎞ ⎠ ⎟ = F (E > E A, T) = \int \infty E A f (E, T) d E (3-22)

$\begin{matrix} (\begin{matrix} Fraction of \\ Molecules & E > E_{A} \\ with \end{matrix}) = F (E > E_{A}, T) = \int_{E_{A}}^{\infty} f (E, T) d E & (3-22) \end{matrix}$

This fraction is shown by the shaded area for E_A = 2.5 kcal/mole for T = 300 K (heavier shade) and for T = 500 K (lighter shade). One can easily see that for T = 500 K a greater fraction of the collisions that cross the barrier with E_A = 2.5 kcal/mol and react, which is consistent with our observation that the rates of reaction increase with increasing temperature.

For E_A > 3RT, we can obtain an analytical approximation for the fraction of molecules of collision with energies greater than E_A by combining Equations (3-21) and (3-22) and integrating to get

⎡ ⎣ ⎢ Fraction of collision with energies greater than E ⎤ ⎦ ⎥ = F (E > E A, T) ≅ 2 π \sqrt (E A R T) 1 / 2 exp (- E A R T) (3-23)

$\begin{matrix} [\begin{matrix} Fraction of collision \\ with energies greater \\ than E \end{matrix}] = F (E > E_{A}, T) ≅ \frac{2}{\sqrt{π}} {(\frac{E_{A}}{R T})}^{1 / 2} exp (- \frac{E_{A}}{R T}) & (3-23) \end{matrix}$

Figure 3-5 shows the fraction of collisions that have energies greater than E_A as as function of the choose E_A at two different temperatures. One observes for an activation energy E_A of 20 kcal/mol and a temperature of 300 K the fraction of collisions with energies greater than 20 kcal/mol is 1.76 X 10~¹⁴ while at 600 K, the fraction increases to 2.39 X 10~⁷, which is a 7 orders of magnitude difference.

$Graph shows two straight lines representing the fraction of collision with energies greater than E subscript A.$

Figure 3-5 Fraction of collision with energies greater than E_A.

So to explain and give insight to the dependence of rate of reaction on concentration and temperature we introduced three concepts

Concept 1	The rate increases with increasing reactant concentration,
Concept 2	The rate is related to the potential energy barrier height and to the conversion of translational energy into potential energy, and
Concept 3	The rate increases with the increasing fraction of collisions that have sufficient energy to cross over the barrier and form products.

To carry this discussion to the next level is beyond the scope of this text as it involves averaging over a collection of pairs of molecules to find an average rate with which they pass over the transition state to become products.

Recapping the last section, the energy of the individual molecules falls within a distribution of energies some molecules have more energy than others. One such distribution is the Boltzmann distribution, shown in Figure 3-4, where f(E, T) is the energy distribution function for the kinetic energies of the reacting molecules. It is interpreted most easily by recognizing the product [f(E, T) dE] as the fraction of molecular collisions that have an energy between E and (E + dE). For example, in Figure 3-4, the fraction of collisions that have energies between 0.25 kcal/mol and 0.35 kcal/mol is 0.081, as shown by the shaded area on the left. The activation energy has been equated with a minimum energy that must be possessed by reacting molecules before the reaction will occur. The fraction of the molecular collisions that have an energy E_A or greater is shown by the shaded areas at the right in Figure 3-4. Figure 3-5 shows the fraction of collisions with energies greater than as a function of E_A at two different temperatures.

3.3.3 The Arrhenius Plot

Postulation of the Arrhenius⁴ equation, Equation (3-18), remains the greatest single advancement in chemical kinetics, and retains its usefulness today, more than a century later. The activation energy, E, is determined experimentally by measuring the reaction rate at several different temperatures. After taking the natural logarithm of Equation (3-18), we obtain

⁴ Arrhenius bio: http://www.umich.edu/~elements/5e/03chap/summary-bioarr.html.

in k A = in A - E R (1 T) (3-24)

$\begin{matrix} in k_{A} = in A - \frac{E}{R} (\frac{1}{T}) & (3-24) \end{matrix}$

We see that the activation energy can be found from a plot of In k_A as a function of (1/T), which is called an Anhenius plot. As can be seen in Figure 3-6 he larger the activation energy, the larger the slope and the more temperature-sensitive the reaction. That is, for large E, an increase in just a few degrees in temperature can greatly increase k and thus increase the rate of reaction. The units of k_A will depend on the reaction order, and the fact that k in Figure 3-6 has units of s"¹ indicates the reaction here is first order.

Calculation of the activation energy

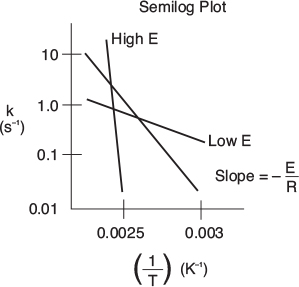
Figure 3-6 Calculation of the activation energy from an Arrhenius plot.

Tutorials

Example 3-1 Determination of the Activation Energy

Calculate the activation energy for the decomposition of benzene diazonium chloride to give chlorobenzene and nitrogen

Decomposition of benzene diazonium chloride to give chlorobenzene and nitrogen is depicted.

using the information in Table E3-1.1 for this first-order reaction.

TABLE E3-1.1 DATA

k (s^-1)	0.00043	0.00103	0.00180	0.00355	0.00717
T (K)	313.0	319.0	323.0	328.0	333.0

Solution

We start by recalling Equation (3-20)

in k A = in A - E R (1 T) (3-24)

$\begin{matrix} in k_{A} = in A - \frac{E}{R} (\frac{1}{T}) & (3-24) \end{matrix}$

We can use the data in Table E3-1.1 to determine the activation energy, E, and frequency factor, A, in two different ways. One way is to make a semilog plot of k vs. (1/T) and determine E from the slope (–E/R) of an Arrhenius plot. Another way is to use Excel or Polymath to regress the data. The data in Table E3-1.1 was entered in Excel and is shown in Figure E3-1.1, which was then used to obtain Figure E3-1.2.

Screenshot shows an excel spreadsheet for figureE3-1 with column headers, k of s inverse, natural logarithm of k, and (1 over T) of (K inverse) and the corresponding values in five rows.

Figure E3-1.1 Excel spreadsheet.

Step-by-step tutorials on how to construct spreadsheets in Polymath and in Excel are on the Web site at http://lumich.edu/~elements/5e/sofiware/polymath-tutorial-inearpolyregression.html and http://umich.edu/~elements/5e/live/chapter03/Excel_tutorial.pdf.

Graph (a) represents excel semilog plot and graph (b) represents excel normal plot after taking natural logarithm of k.

"In graph (a), the horizontal axis representing “(1 over T) of (K inverse)” ranges from 0.00295 to 0.00325, in increments of 0.00005. 0.0001, 0.001, and 0.01 are marked on the vertical axis represents “k of (secant inverse).” A line segment passing through five points that slide from left to right labeled “k equals 1.32 times (10 to the power of 16) times (e to the power of (negative 14017 over T)) is shown. In graph (b), 0.0030, 0.0030, 0.0031, 0.0031, 0.0032, 0.0032, and 0.0033 are marked on the horizontal axis represents “(1 over T) of (K inverse).” Negative 8.0, negative 7.0, negative 6.0, negative 5.0, and negative 4.0 are marked on the vertical axis represents “natural logarithm of (k).” A line segment passing through five points that slide from left to right labeled, “natural logarithm of k equals (negative 14017 over T) plus 37.12.”"

Figure E3-1.2 (a) Excel semilog plot; (b) Excel normal plot after taking ln(k). (http://wwwMmichxdu/~demmts/5e/sofWare/polymath-tutorial-linearpolyregression.html)

k = k 1 exp [E R (1 T 1 - 1 T)]

$k = k_{1} \exp [\frac{E}{R} (\frac{1}{T_{1}} - \frac{1}{T})]$

The equation for the best fit of the data

ln k = - 14 , 017 T + 37.12 (E3-1.1)

$\begin{matrix} \ln k = \frac{- 14, 017}{T} + 37.12 & (E3-1.1) \end{matrix}$

is also shown in Figure E3-1.2(b). From the slope of the line given in Figure 3-1.2(b) and Equation (3-20), we obtain

- E R = - 14, 017 K E = (14, 017 K) R = (14, 017 K) (8.314 J mol \cdot K)

$\begin{matrix} - \frac{E}{R} = - 14, 017 K \\ E = (14, 017 K) R = (14, 017 K) (8.314 \frac{J}{mol \cdot K}) \end{matrix}$

E = 116.5 kJ mol

$E = 116.5 \frac{kJ}{mol}$

From Figure E3-1.2(b) and Equation (E3-1.1), we see

In A = 37.12

Taking the antilog, we find the frequency factor to be

A = 1.32 \times 1016 s - 1 k = 1.32 \times 1016 e x p [- 14 , 017 K T] (E 3-1.2)

$\begin{matrix} A = 1.32 \times 10^{16} s^{- 1} \\ k = 1.32 \times 10^{16} e x p [- \frac{14, 017 K}{T}] & (E 3–1.2) \end{matrix}$

Analysis: The activation energy, E, and frequency factor, A, can be calculated if we know the specific reaction rate, k, at two temperatures, T₁ and T₂. We can either use the Arrhenius Equation (3-18) twice, once at T₁ and once at T₂, to solve two equations for the two unknowns, A and E, or we can take the slope of a plot of (In k) as a function of (1/T); the slope will be equal to (–E/R).

The rate does not temperature increase of 10°C

A thumbs up symbol with stop icon is shown.

There is a rule of thumb that states that the rate of reaction doubles for every 10°C increase in temperature. However, this rule is true only for specific combinations of activation energies and temperatures. For example, if the activation energy is 53.6 KJ/mol, the rate will double only if the temperature is raised from 300 K to 310 K. If the activation energy is 147 KJ/mol, the rule will be valid only if the temperature is raised from 500 K to 510 K (see Problem P3-7_B for the derivation of this relationship).

A most useful form of k(T)

The larger the activation energy, the more temperature-sensitive is the rate of reaction. While there are no typical values of the frequency factor and activation energy for a first-order gas-phase reaction, if one were forced to make a guess, values of A and E might be 10¹³ s^_1 and 100 kj/mol. However, for families of reactions (e.g., halogenation), a number of correlations can be used to estimate the activation energy. One such correlation is the Polanyi-Semenov equation, which relates activation energy to the heat of reaction (see Professional Reference Shelf R3.1). Another correlation relates the activation energy to differences in bond strengths between products and reactants.⁵ While the activation energy cannot be currently predicted a priori, significant research efforts are under way to calculate activation energies from first principles.⁶

⁵ M. Boudart, Kinetics of Chemical Processes (Upper Saddle River, NJ: Prentice Hall), p. 168. J. W. Moore and R. G. Pearson, Kinetics and Mechanisms, 3rd ed. (New York: Wiley), p. 199. S. W. Benson, Thermochemical Kinetics, 2nd ed. (New York: Wiley).

⁶ R. Masel, Chemical Kinetics and Catalysis, New York: Wiley, 2001, p. 594.

One final comment on the Arrhenius equation, Equation (3-18). It can be put in a most useful form by finding the specific reaction rate at a temperature T₀; that is,

and taking the ratio to obtain

k (T 0) = A e - E / R T 0

$k (T_{0}) = {A e}^{- E / R T_{0}}$

and at a temperature T

k (T) = A e - E / R T

$k (T) = {A e}^{- E / R T}$

and taking the ratio to obtain

K (T) = K (T 0) e E R (1 T 0 - 1 T) (3 - 25)

$K (T) = K (T_{0}) e^{\frac{E}{R} (\frac{1}{T_{0}} - \frac{1}{T})} (3 - 25)$

This equation says that if we know the specific reaction rate k(T₀) at a temperature, T₀, and we know the activation energy, E, we can find the specific reaction rate k(T) at any other temperature, T, for that reaction.

3.4 Molecular Simulations

3.4.1 Historical Perspective

For the last five or ten years, molecular simulations have been used more and more to help understand chemical reactions along with their pathways and mechanisms. Consequently, to introduce you to this area we will use MATLAB to simulate a simple reaction and view a couple of molecular simulation trajectories. Some of the earliest simulations were carried out by Professor Martin Karplus more than 50 years ago and are described in his groundbreaking journal article J. Chem. Phys. 43 p. 3259 (1965) for the reaction

A + BC → AB + C

The forces and potential energies he used to describe the interaction as the two molecules approach each other are described in the Professional Reference Shelf R3.3 (PRS R3.3) (http://www.umich.edu/~elements/5e/03chap/prof-moldyn.html).

In Karplus’s procedure, the trajectories and molecular collisions are calculated and analyzed to determine whether or not they have sufficient transla-tional, vibrational, and kinetic energy along with molecular orientation to either react or not react. A nonreactive trajectory and a reactive trajectory are shown in Figures 3-7(a) and 3-7(b), respectively. One notes the vibrations of the AB and BC molecules from the plot of R_AB and R_BC with time. In the Monte Carlo simulation the randomly chosen input parameters are (1) the initial distance between A and BC, (2) the orientation of BC relative to A, and

Nonreactive Trajectory (a)

In Nonreactive trajectory (a), three molecules are shown. Molecule A (bottom) is connected to the molecule B (top,) at the distance of R subscript AB. The molecule B is connected to the molecule C (middle right) at the distance of R subscript BC. Two horizontal lines are drawn for molecule A and molecule B with molecule C labeled "b" forms molecule A at the bottom and molecule B connected to molecule C at the top. The graph on its right corresponding to the process shows the horizontal axis representing "R" and the vertical axis representing "t." A curve with four bumps is shown from the vertical axis near the origin labeled "R subscript BC." Above the curve, two irregular U-shaped curves labeled "R subscript A" and "R subscript AC" are shown respectively. In Reactive trajectory (a), three molecules are shown. Molecule A at the bottom with a forward arrow and molecule B connected to molecule C at the top. Two horizontal lines are drawn for molecule A and molecule B with molecule C labeled "b" reacts to form molecule A connected to molecule B at the top and molecule C at the bottom. The graph on its right corresponding to the process shows the horizontal axis representing "R" and the vertical axis representing "time." A curve with four bumps is shown from the vertical axis near the origin on the left labeled "R subscript BC" and on the right labeled "R subscript AB." A decreasing curve starts from a point R on the vertical axis labeled "R subscript AB," then touches the curve, and slides up gradually labeled "R subscript BC." A small vertical line is drawn touching the intersection point of decreasing curve and the second bump of the curve is labeled "t subscript 1."

Reactive Trajectory (b)

Figure 3-7 Molecular Trajectories (a) Nonreactive (b) Reactive.

(3) the angular momentum of BC. Next, the reaction trajectories are calculated to learn whether the trajectory is reactive or nonreactive and the result is recorded. This process is repeated a number of times for different random input parameters and the number of reactive and nonreactive trajectories for these input parameters are again counted and recorded. The statistics of the number of reactive versus number of nonreactive trajectories are then used to develop a probability of reaction. The specific reaction rate constant and the activation energy are determined from the probability of reaction (cf. PRS R3.3).

Professor Karplus received the 2013 Nobel Prize for his pioneering work in molecular simulations.

3.4.2 Stochastic Modeling of Reactions⁷

⁷ An overview of stochastic modeling can be found in a PowerPoint presentation on the Web site (http://www.docAc.ac.uk/~jb/confermces/pasta2006/slides/stochastic-simulation-introduction.pdf.

However, rather than tracking singular trajectories as Karplus did, we consider an ensemble of molecules and the collisions between both reactants and products and use stochastic modeling to determine the concentration trajectories of the reacting molecules. To illustrate the stochastic modeling of chemical reactions we will use the reversible reaction

A + B→←krkfC + D $\begin{matrix} A + B & {\begin{matrix} \to \\ \leftarrow \end{matrix}}_{k_{r}}^{k_{f}} C + D \end{matrix}$

which we will write as separate reactions

A+B - \to - - - - - - - - k f C+D (1)

$\begin{matrix} A+B \overset{k_{f}}{\to} C+D & (1) \end{matrix}$

C+D - \to - - - - - - - - k f A+B (2)

$\begin{matrix} C+D \overset{k_{f}}{\to} A+B & (2) \end{matrix}$

that are assumed to be elementary and have deterministic rate laws given by –r_A = k_fC_AC_B and –r_C = k_rC_CC_D.

To model these reactions stochastically we define the probability that the “reaction i” will occur per unit time, i.e., r_i. This probability is related to the number of ways the reaction can occur per unit time, which is analogous to the deterministic rate law. The probability function of Reaction (1) occurring per unit time, r_f, is

r f = k f x A x B (3-26)

$\begin{matrix} r_{f} = k_{f} x_{A} x_{B} & (3-26) \end{matrix}$

and the probability function of Reaction (2) occurring per unit time is

r r = k r x C x D (3-27)

$\begin{matrix} r_{r} = k_{r} x_{C} x_{D} & (3-27) \end{matrix}$

where the terms xii $x_{i_{i}}$ are the number of molecules of species i. Here r_f and r_r are the probability functions of the forward and the reverse reactions occurring per unit time and the rate constants k_f and k_r are probabilities that the collisions between molecules A and B give rise to Reaction (1) or between molecules C and D giving rise to Reaction (2) respectively. The rate constants k_f and k_r have [1(no. of molecules)2s] $[\frac{1}{({no. of molecules)}^{2} s}]$ . The total reaction probability function, r_t, is

rt=rf+rr.(3-28) $\begin{matrix} r_{t} = r_{f} + r_{r} . & (3-28) \end{matrix}$

In carrying out the stochastic simulations we randomly choose which reaction, i.e., either (1) or (2), will occur in time step t_i based on the reactive probabilities of each of the two reactions. The probability of Reaction (1) occurring is related to the ratio

f 1 = r f r f + r r = k f x A x B k f x A x B + k r x C x D (3-29)

$\begin{matrix} f_{1} = \frac{r_{f}}{r_{f} + r_{r}} = \frac{k_{f} x_{A} x_{B}}{k_{f} x_{A} x_{B} + k_{r} x_{C} x_{D}} & (3-29) \end{matrix}$

and the probability of Reaction (2) occurring is related to the ratio

f 2 = r r r f + r r = k f x C x D k f x A x B + k r x C x D (3-30)

$\begin{matrix} f_{2} = \frac{r_{r}}{r_{f} + r_{r}} = \frac{k_{f} x_{C} x_{D}}{k_{f} x_{A} x_{B} + k_{r} x_{C} x_{D}} & (3-30) \end{matrix}$

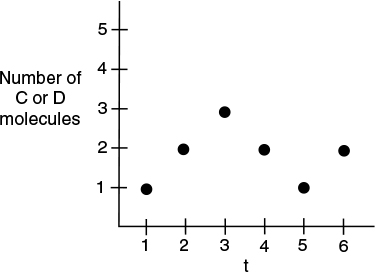
Next, we generate a random number, p₁ in the interval (0, 1). If(0<p₁ <f₁ then Reaction (1) occurs and the number of A and B molecules decrease and the number of C and D molecules increase. If p₁ was not in that interval then Reaction (2) occurs. Consequently, the probability values of f₁ and f₂ will change for the next time step and for the next random number generation. Let’s consider the first six time steps in which the probability results show that Reaction (1) takes place in the first three time steps, while Reaction (2) occurs in the fourth and fifth time steps, and then Reaction (1) occurs again in the sixth time step. The number of C or D molecules after the first six steps are l → 2 → 3 → 2 → 1 → 2 as shown in Figure 3-8.

Graph shows the relationship of the number of molecules as a function of t.

Figure 3-8 Number of molecules as a function of t.

If we continued the time steps in this fashion, the overall number of C and D molecules would continue to increase in a stochastic manner as shown in Figure 3-9(b). Analogously the number of A and B molecules would continue to decrease, also shown in this figure. Stochastic modeling allows us to see on a molecular level how the reaction progresses. The takeaway lesson is that while the deterministic model shows the smooth reaction path of species C and D being formed, on the molecular scale we see C and D being formed, then reacting back to A and B and then being formed again.

The time between a molecular collision of A and B is also random. To determine this time, we generate a random number, p₂ (0 < p₂ < 1), and the time increment is

Δ t i = ln ( 1 p 2 ) r t (3-31)

$\begin{matrix} Δ_{t_{i}} = \frac{\ln (\frac{1}{p_{2}})}{r_{t}} & (3-31) \end{matrix}$

where Δt_i has the units of seconds. We update the time t by the equation

t_i+1 = t_r + Δt_i (3-32)

The graphical user interface in LEP shows the input fields for the parameters kf: 1, kb: 1, A: 40, B: 40, C: 0, and D: 0. A Run button (selected) and a Stop button are shown at the bottom.

Figure 3-9(a) Graphical user interface in LEP.

The graphical representation of the relationship between time and number of molecules is shown.

Figure 3-9(b) Molecular trajectories.

Schematic shows a maze puzzle for finding the way with a start point, correct way, and an end point.

Where are we?

Figure 3-9(b) shows how the number of molecules of species A and C fluctuate as the reaction progresses.

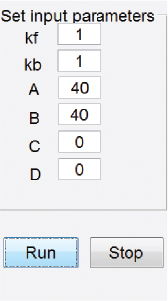
Now go to the LEP on molecular simulations and use the Graphical User Interface shown in Figure 3-9(a) to vary the number of molecules initially along with rate constants k_f and k_r (cf. LEP P3-1_A (b)) and observe the trajectories similar to the one shown in Figure 3-9(b). A tutorial on how to run the simulation is given on the Web site along with the simulation of a series reaction (A + B ⇄ C + D ⇄ E + F).

3.5 Present Status of Our Approach to Reactor Sizing and Design

In Chapter 2, we combined the different reactor mole balances with the definition of conversion to arrive at the design equation for each of four types of reactors, as shown in Table 3-2. Next we showed that if the rate of disappearance is known as a function of the conversion X

–r_A = g(X)

then it is possible to size CSTRs, PFRs, and PBRs operated at the same conditions under which –r_A = g(X) was obtained.

TABLE 3-2 Design Equations

	Differential Form	Algebraic Form	Integral Form
Batch	NA0dXdt=−rAV00000(2−6) $N_{A0} \frac{d X}{d t} = - r_{A} V (2 - 6)$		t=NA0∫X0dX−rAV000000(2−9) $t = N_{A0} \int_{0}^{X} \frac{d X}{- r_{A} V} (2 - 9)$
Backmix (CSTR)		V=FA0X−rA000000(2−13) $V = \frac{F_{A0} X}{- r_{A}} (2 - 13)$
Fluidized CSTR		W=FA0X−r′A $W = \frac{F_{A0} X}{- r_{A}^{'}}$
Tubular (PFR)	FA0dXdV=−rA00000(2−15) $F_{A0} \frac{d X}{d V} = - r_{A} (2 - 15)$		V=FA0∫X0dX−rA000000(2−16) $V = F_{A0} \int_{0}^{X} \frac{d X}{- r_{A}} (2 - 16)$
Packed bed (PBR)	FA0dXdW=−r′A00000(2−17) $F_{A0} \frac{d X}{d W} = - r_{A}^{'} (2 - 17)$		W=FA0∫X0dX−r′A000000(2−18) $W = F_{A0} \int_{0}^{X} \frac{d X}{- r_{A}^{'}} (2 - 18)$

In general, information in the form – r_A = g(X) is not available. However, we have seen in Section 3.2 that the rate of disappearance of A, – r_A, is normally expressed in terms of the concentration of the reacting species. This functionality

–r_A = [k_A(T)][fn(C_A,C_B, ...)] (3-2)

- r A = f (C j) + C j = h j (X) ⏐ ↓ - r A = g (X)

$\begin{matrix} - r_{A} = f (C_{j}) \\ + \\ \begin{matrix} C_{j} = h_{j} (X) \\ ↓ \\ \begin{matrix} - r_{A} = g (X) \end{matrix} \end{matrix} \end{matrix}$

and then we can design isothermal reactors

is called a rate law. In Chapter 4, we show how the concentration of the reacting species maybe written in terms of the conversion X

C_j = h_j (X) (3-26)

With these additional relationships, one observes that if the rate law is given and the concentrations can be expressed as a function of conversion, then in fact we have –r_A as a function of X and this is all that is needed to evaluate the isothermal design equations. One can use either the numerical techniques described in Chapter 2 or, as we shall see in Chapter 5, a table of integrals, and/or software programs (e.g., Polymath).

The CRE Algorithm

• Mole Balance, Ch 1

• Rate Law, Ch 3

• Stoichiometry, Ch 4

• Combine, Ch 5

• Evaluate, Ch 5

• Energy Balance, Ch 11

Closure. Having completed this chapter, you should be able to write the rate law in terms of concentration and the Arrhenius temperature dependence. We have now completed the first two basic building blocks in our algorithm to study isothermal chemical reactions and reactors.

Figure shows the first two building blocks labeled Rate Law and Mole Balance.

In Chapter 4, we focus on the third building block, stoichiometry, as we use the stoichiometric table to write the concentrations in terms of conversion to finally arrive at a relationship between the rate of reaction and conversion.

Summary

1. Relative rates of reaction for the generic reaction:

A + b a B \to c a C + d a D (S 3-1)

$\begin{matrix} A + \frac{b}{a} B \to \frac{c}{a} C + \frac{d}{a} D & (S 3-1) \end{matrix}$

The relative rates of reaction can be written either as

- r A a = - r B b = - r C c = - r D d o r r A - a = r B - b = r C c = r D d (S 3 - 2)

$\frac{- r_{A}}{a} = \frac{- r_{B}}{b} = \frac{- r_{C}}{c} = \frac{- r_{D}}{d} o r \frac{r_{A}}{- a} = \frac{r_{B}}{- b} = \frac{r_{C}}{c} = \frac{r_{D}}{d} (S 3 - 2)$

2. Reaction order is determined from experimental observation:

A+B−→−−−−−−−−−−C−rA=KCαACβB000000000000000000000000000000000(S3-3) $\begin{array}{l} A+B \to C \\ - r_{A} = K C_{A}^{α} C_{B}^{β} \end{array} (S3-3)$

The reaction in Equation (S3-3) is a order with respect to species A and β order with respect to species B, whereas the overall order, n, is (α + β). If a = 1 and β = 2, we would say that the reaction is first order with respect to A, second order with respect to B, and overall third order. We say a reaction follows an elementary rate law if the reaction orders agree with the stoichiometric coefficients for the reaction as written.

Examples of reactions that follow an elementary rate law:

Irreversible reactions
First order
C2H6→C2H4+H2 $C_{2} H_{6} \to C_{2} H_{4} + H_{2}$	$- r C 2 H 6 = K C C 2 H 6$ $- r_{_{C_{2}} H_{6} =} K C_{_{C_{2}} H_{6}}$
Second order
CNBr+CH3NH2→CH3Br+NCNH2 $CNBr+ C H_{3} {NH}_{2} \to C H_{3} Br + {NCNH}_{2}$	$- r CNBr = K C CNBr C CH 3 NH 2$ $- r_{CNBr} = K C_{_{CNBr}} C_{{CH}_{3}}_{{NH}_{2}}$
Reversible reactions
Second order
$2 C 6 H 6 ⇌ C 12 H 10 +H 2$ $2 C_{6} H_{6} ⇌ C_{12} H_{10} {+H}_{2}$	$- r C 2 H 6 = K C 2 H 6 (C 2 C 6 H 6 - C C 12 H 10 C H 2 K C)$ $- r_{C_{2} H_{6}} = K_{C_{2} H_{6}} (C^{2}_{C_{6} H_{6}} - \frac{C_{C_{12} H_{10}} C_{H_{2}}}{K_{C}})$
Examples of reactions that follow nonelementary rate laws:
Homogeneous
$CH 3 CHO \to CH 4 + CH 2$ ${CH}_{3} CHO \to {CH}_{4} + {CH}_{2}$	$- r CH 3 CHO = K C 3 / 2 CH 3 CHO$ $- r_{{CH}_{3} CHO} = K C_{{CH}_{3}}^{3 / 2} CHO$
Heterogeneous reactions
$C 2 H 4 + H 2 \to c a t C 2 H 6$ $C_{2} H_{4} + H_{2} \underset{c a t}{\to} C_{2} H_{6}$	$- r C 2 C 4 = K P C 2 H 4 P H 2 1 + K C 2 H 4 P C 2 H 4$ $- r_{C_{2} C_{4}} = K \frac{P_{C_{2} H_{4}} P_{H_{2}}}{1 + K_{C_{2} H_{4}} P_{C_{2} H_{4}}}$

3. The temperature dependence of a specific reaction rate is given by the Arrhenius equation

k = A_e^−E/RT (S3-4)

where A is the frequency factor and E the activation energy.

If we know the specific reaction rate, k, at a temperature, T₀, and the activation energy, we can find k at any temperature, T

k(T)=k(T0)exp[ER(1T0−1T)](S3-5) $\begin{matrix} k (T) = k (T_{0}) \exp [\frac{E}{R} (\frac{1}{T_{0}} - \frac{1}{T})] & (S 3-5) \end{matrix}$

Concept 1	The rate increases with increasing reactant concentrations,
Concept 2	The rate is related to the potential barrier height and to the conversion of translational energy into potential energy, and
Concept 3	The rate increases as the fraction of collisions that have sufficient energy to cross over the barrier and form products increases.

Similarly from Appendix C, Equation (C-9), if we know the partial pressure equilibrium constant K_P at a temperature, T₁ and the heat of reaction, we can find the equilibrium constant at any other temperature

K P (T) = K P (T 1) exp [Δ H o R x R (1 T 1 - 1 T)] (C-9)

$\begin{matrix} K_{P} (T) = K_{P} (T_{1}) \exp [\frac{Δ H_{R x}^{o}}{R} (\frac{1}{T_{1}} - \frac{1}{T})] & (C-9) \end{matrix}$

CRE Web Site Materials

• Expanded Material (http://umich.edu/~elements/5e/03chap/expanded.html)

1. Collision Theory (http://umich.edu/~elements/5e/03chap/pdf/CollisionTheory.pdf)

2. Transition State (http://umich.edu/~elements/5e/03chap/pdf/TransitionState.pdf

3. Molecular Dynamics (http://umich.edu/~elements/5e/03chap/pdf/MolecularDynamic.pdf

4. How to Estimate the Activation Energy from the Polanyi Equation

5. Web P3-1_A Puzzle Problem “What’s Wrong with This Solution?” (http://umich.edu/~elements/5e/03chap/expanded_ch03_puzzle.pdf

6. Additional Homework Problems (http://lumich.edu/~elements/5e/03chap/add-cdp3b.html)

• Learning Resources (http://lumich.edu/~elements/5e/03chap/learn.html)

1. Summary Notes (http://lumich.edu/~elements/5e/03chap/summary.html)

2. Self-Tests

A. Exercises (http://lumich.edu/~elements/5e/03chap/all-selfiest.html)

B. i>clicker Questions (http://www.umich.edu/~elements/5e/03chap/iclicker_ch3_ql.html)

3. Web Module

A. Cooking a Potato (http://www.umich.edu/~elements/5e/web_mod/potato/index.htm) Chemical reaction engineering is applied to cooking a potato

Starch (crystalline) \to k Starch amorphous

$Starch (crystalline) \overset{k}{\to} Starch amorphous$

with

k = Ae^–E/RT

A set of three photographs show cross sections of a boiled potato after 8 minutes, 12 minutes, and 16 minutes at 400 degrees Fahrenheit.

B. Molecular Reaction Engineering

Molecular simulators (e.g., Gaussian) are used to make predictions of the activation energy (http://www.umich.edu/~elements/5e/web_mod/quantum/index.htm)

• FAQs (Frequently Asked Questions) (http://umich.edu/~elements/5e/03chap/faq.html)

• Professional Reference Shelf (http://umich.edu/~elements/5e/03chap/prof.html)

R3.1 Collision Theory (http://umich.edu/~elements/5e/03chap/prof-collision.html)

In this section, the fundamentals of collision theory

Schematic representation shows a collision cross section theory.

Figure R3.1 Schematic of collision cross section.

are applied to the reaction

A + B → C + D

to arrive at the following rate law

The equation to arrive the rate law is shown.

- r A = π σ 2 A B (8 π k B T μ π) 1 / 2 N Avo                            A e - E A / R T C A C B = A e - E A / R T C A C B

$- r_{A} = \underset{A}{\underset{︸}{π σ_{A B}^{2} {(\frac{8 {πk}_{B} T}{μπ})}^{1 / 2} N_{Avo}}} e^{- E_{A} / R T} C_{A} C_{B} = A e^{- E_{A} / R T} C_{A} C_{B}$

The activation energy, E_A, can be estimated from the Polanyi equation

EA=EoA+γPΔHRx $E_{A} = E_{A}^{o} + γ_{P} Δ H_{R x}$

R3.2 Transition-State Theory (http://umich.edu/~elements/5e/03chap/prof-transition.html) In this section, the rate law and rate-law parameters are derived for the reaction

A + BC ⇄ ABC^# → AB + C

using transition-state theory. Figure PW3B-1 shows the energy of the molecules along the reaction coordinate, which measures the progress of the reaction.

A set of three graphs show Reaction coordinate for (a) S subscript (N2) reaction, and (b) generalized reaction. The third figure (c) shows a 3-D energy surface for generalized reaction.

"Graph (a) shows Energy along the vertical axis and a bell shaped curve. The left end is slightly lifted and labeled “A plus BC,” and the right end is closer to the horizontal axis and labeled “AB plus C.” The peak of the curve is labeled “A minus B minus C6.” The vertical interval between the left end and the peak is labeled “E subscript b.” Graph (b) shows Energy along the vertical axis and a bell shaped curve. A parabola intersects the bell curve at the left, right, and the peak. The parabola at the left is labeled “BC plus A,” at the peak is labeled “ABC,” and at the right is labeled “AB plus C.” Figure (c) shows A minus B along the x-axis, B minus C along the y-axis, and Potential energy along the z-axis. The activated state, reaction path, initial state A plus BC, Final State A minus B plus C and Completely disassociated state A plus B plus C are labeled."

Figure PW3B-1 Reaction coordinate for (a) S_N2 reaction, and (b) generalized reaction, (c) 3-D energy surface for generalized reaction.

R3.3 Molecular Dynamics Simulations (http://umich.edu/~elements/5e/03chap/prof-moldyn.html) The reaction trajectories are calculated to determine the reaction cross section of the reacting molecules. These trajectories, which are identified as either (1) nonreactive or (2) reactive, are shown in Figure 3-7. The reaction probability is found by counting up the number of reactive trajectories after Karplus.⁸ Professor Karplus received the 2013 Nobel Prize for his work on Molecular Dynamic Simulations.

⁸ M. Karplus, R. N. Porter, and R. D. Sharma, J. Chem. Phys., 43 (9), 3259 (1965).

Questions and Problems

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.

A = ● B = ◼ C = ◆ D = ◆◆

Questions

Q3-1_A i>clicker. Go to the Web site (http://www.umich.edu/~elements/5e/03chap/iclicker_ch3_ql.html) and view at least five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case: explain why the question should not be on the next exam. For either case, explain your reasoning.

Q3-2_C (a) List the important concepts that you learned from this chapter. What concepts are you not clear about?

(b) Explain the strategy to evaluate reactor design equations and how this chapter expands on Chapter 2.

(c) Listen to the audios on the CRE Web site. Select a topic and explain it.

(d) Which example on the CRE Web site’s Summary Notes for Chapters 1 through 3 was most helpful?

Computer Simulations and Experiments

P3-1_B (a) LEP: Variation of Energy Distribution with Temperature. Wolfram

(i) Vary temperature, T, and activation energy, E, to learn their effects on energy distribution curve. Specifically, vary the parameters between their maximum and minimum values (i.e., high T, low E; low T, low E; high T, high E; etc.) and write a few sentences describing what you find.

(ii) What should be the minimum temperature so that at least 50% molecules have energy greater than the activation energy you have chosen (e.g., 6 kcal/mol)?

(iii) After reviewing Generating Ideas and Solutions on the Web site (http://www.umich.edu/~ele-ments/5e/toc/SCPS,3rdEdBook(Ch07).pdf). Choose one of the brainstorming techniques (e.g., lateral thinking) to suggest two questions that should be included in this problem.

(b) LEP Molecular Simulations.

(i) For k_f = k_f = 1.0 Run the simulation when the number of A and B are

(a) A = 20 B = 20 C = D = 0

(b) A = 200 B = 200 C = D = 0

(d) A = 200 B = 2,000 C = D = 0

Is there any effect of the experiments (a) through (d) on the equilibrium concentration? What about the time taken to attain equilibrium?

What conclusions do you draw from your experiments?

(ii) For 100 A molecules and 100 B molecules, vary the specific reaction rate constants k_f and k_r and describe the differences in trajectories you observe,

(iii) What happens when you set either k_f or k_r to zero?

(iv) Why are there fluctuations in the concentration trajectories? Why are they not smooth? What causes the size of the fluctuations to increase or decrease?

(v) What do you observe when you increase the initial number of molecules? Can you explain your observations?

(vi) Do the reactions stop once equilibrium is reached?

(vii) Write a conclusion on what you found in experiments (i) through (vi).

Problems

(c) Example 3-1. Activation Energy. In the Excel spreadsheet, replace the value of k at 372.5 K with k = 0.0009^-1s and determine the new values of E and k.

(d) Example 3-1. Make a plot of k versus T and In k versus (1/T) for E = 240 KJ/mol and for E = 60 KJ/mol. (1) Write a couple of sentences describing what you find. (2) Next, write a paragraph describing the activation energy and how it affects chemical reaction rates, and what its origins are.

(e) Collision Theory—Professional Reference Shelf. Make an outline of the steps that were used to derive

–r_A = Ae^–E/RT C_AC_B

(f) The rate law for the reaction (2A + B → C) is −rA=kAC2ACB $- r_{A} = k_{A} C_{A}^{2} C_{B}$ with k_A = 25(dm³/mol)²/s. What are k_B and k_c?

P3-2_B Molecular collision energies—refer to Figure 3-3 and to the LEP 3-1. cdf Variation of Energy Distribution with Temperature.

(a) What fraction of molecular collisions have energies less than or equal to 2.5 kcal at 300 K? At 500 K?

(b) What fraction of molecular collisions have energies between 3 and 4 kcal/mol at T = 300 K? At T = 500K?

(c) What fraction of molecular collisions have energies greater than the activation energy E_A = 25 kcal at T = 300 K? At T = 500K?

P3-3_B (a) Use Figure 3-l(b) to sketch the trajectory over the saddle point when the BC and AB molecules vibrate with the minimum separation distance being 0.20 Angstroms and the maximum separation being 0.4 Angstroms.

(b) At point Y, R_AB = 2.8 Angstroms, sketch the potential energy as a function of the distance R_BC noting the minimum at valley floor.

(c) At Point X, R_BC = 2.8 Angstroms, sketch the potential energy as a function of R_AB noting the minimum on the valley floor.

P3-4_B Use Equation (3-20) to make a plot of f(E,T) as a function of E for T = 300, 500, 800, and 1200 K.

(a) What is the fraction of molecules that have sufficient energy to pass over a energy barrier of 25 kcal at 300, 500, 800, and 1200 K?

(b) For a temperature of 300 K, what is the ratio of the faction of energies between 15 and 25 kcal to the same energy range (15-25 kcal) at 1200 K?

(c) Make a plot of F(E > E_A,T) as a function of (E_A/RT) for (E_A/RT) > 3. What is the fraction of collisions that have energies greater than 25 kcal/mole at 700 K?

(d) What fraction of molecules have energies greater than 15 kcal/mol at 500 K?

(e) Construct a plot of F(E > E_A,T) versus T for E_A = 3, 10, 25, and 40 kcal/mole. Describe what you find. Hint: Recall the range of validity for T in Equation (3-23).

P3-5a The following figures show the energy distribution function at 300 K for the reaction A + B → C

Graph shows an energy distribution function at 300 K.

Figure P3-5(a)

Figure P3-5(b)

For each figure, determine the following:

(a) What fraction of the collisions have energies between 3 and 5 kcal/mol?

(b) What fraction of collisions have energies greater than 5 kcal/mol? (Ans.: Figure P3-5 (b) fraction = 0.28)

(c) What is the fraction with energies greater than 0 kcal/mol?

(d) What is the fraction with energies 8 kcal/mol or greater?

(e) If the activation energy for Figure P3-5(b) is 8 kcal/mol, what fraction of molecules have an energy greater than E_A?

(f) Guess what (sketch) the shape of the curve f(E,T) versus £ shown in Figure P3-5(b) would look like if the temperature were increased to 400 K. (Remember: ∫∞0f(E,T)dE=1.) $\int_{0}^{\infty} f (E, T) d E = 1.)$

P3-6_A The frequency of fireflies flashing and the frequency of crickets chirping as a function of temperature follow. Source: Keith J. Laidler, “Unconventional applications of the Arrhenius law.” J. Chem. Educ., 5, 343 (1972). Copyright (c) 1972, American Chemical Society. Reprinted by permission.

The running speed of ants and the flight speed of honeybees as a function of temperature are given below. Source: B. Heinrich, The Hot-Blooded Insects (Cambridge, MA: Harvard University Press, 1993).

(a) What do the firefly and cricket have in common? What are their differences?

(b) What is the velocity of the honeybee at 40°C? At -5°C?

(c) Nicolas wants to know if the bees, ants, crickets, and fireflies have anything in common. If so, what is it? You may also do a pair-wise comparison.

(d) Would more data help clarify the relationships among frequency, speed, and temperature? If so, in what temperature should the data be obtained? Pick an insect, and explain how you would carry out the experiment to obtain more data. For an alternative to this problem, see CDP3-A_B.

(e) Data on the tenebrionid beetle whose body mass is 3.3 g show that it can push a 35-g ball of dung at 6.5 cm/s at 27° C, 13 cm/s at 37° C, and 18 cm/s at 40° C.

(1) How fast can it push dung at 41.5° C? Source: B. Heinrich. The Hot-Blooded Insects (Cambridge, MA: Harvard University Press, 1993). (Ans.: 19.2 cm/s at 41.5° C)

Schematic shows a tenebrionid beetle pushing a ball of dung.

(2) Apply one or more of the six ideas in Preface Table P-4, page xxvii, to this problem.

P3-7_B Troubleshooting. Corrosion of high-nickel stainless steel plates was found to occur in a distillation column used at DuPont to separate HCN and water. Sulfuric acid is always added at the top of the column to prevent polymerization of HCN. Water collects at the bottom of the column and HCN collects at the top. The amount of corrosion on each tray is shown in Figure P3-5_B as a function of plate location in the column.

Two schematics show corrosion in a distillation column.

Figure P3-5_B Corrosion in a distillation column.

The bottom-most temperature of the column is approximately 125°C and the topmost is 100°C. The corrosion rate is a function of temperature and the concentration of an HCN-H₂S0₄ complex. Suggest an explanation for the observed corrosion-plate profile in the column. What effect would the column operating conditions have on the corrosion-plate profile?

P3-8_B Inspector Sgt Ambercromby of Scotland Yard. It is believed, although never proven, that Bonnie murdered her first husband, Lefty, by poisoning the tepid brandy they drank together on their first anniversary. Lefty was unaware she had coated her glass with an antidote before she filled both glasses with the poisoned brandy. Bonnie married her second husband, Clyde, and some years later when she had tired of him, she called him one day to tell him of her new promotion at work and to suggest that they celebrate with a glass of brandy that evening. She had the fatal end in mind for Clyde. However, Clyde suggested that instead of brandy, they celebrate with ice-cold Russian vodka and they down it Cossack style, in one gulp. She agreed and decided to follow her previously successful plan and to put the poison in the vodka and the antidote in her glass. The next day, both were found dead. Sgt. Ambercromby arrives. What are the first three questions he asks? What are two possible explanations? Based on what you learned from this chapter, what do you feel Sgt. Ambercromby suggested as the most logical explanation?

Cartoon of a man holding a pipe in a hand and a lens in the other hand.

Who done it?

Source: Professor Flavio Marin Flores, ITESM, Monterrey, Mexico.

[Hint: View the YouTube video (www.youtube.com) made by the chemical reaction engineering students at the University of Alabama, entitled The Black Widow. You can access it from the CRE Web site (www.umich.edu/~elements/5e) using the YouTube Videos link under By Concepts on the home page.]

P3-9_B Activation Energy

(a) The rule of thumb that the rate of reaction doubles for a 10°C increase in temperature occurs only at a specific temperature for a given activation energy. Develop a relationship between the temperature and activation energy for which the rule of thumb holds. Neglect any variations in concentrations. For E_A = 50 kcal/mol, over what temperature range (T₂ = T₁ + 10°C) is this rule of thumb valid?

(b) Write a paragraph explaining activation energy, E, and how it affects the chemical reaction rate. Refer to Section 3.3 and especially the Professional Reference Shelf Sections R3.1, R3.2, and R3.3 if necessary.

P3-10_C The initial reaction rate for the elementary reaction

2A + B → 4C

was measured as a function of temperature when the concentration of A was 2 M and that of B was 1.5 M.

−rA(mol/dm3.s):T(K)0.0023000.0463200.723408.33360 $\begin{matrix} - r_{A} ({mol/dm}^{3} . s) : & 0.002 & 0.046 & 0.72 & 8.33 \\ T(K) & 300 & 320 & 340 & 360 \end{matrix}$

(a) What is the activation energy?

(b) What is the frequency factor?

(c) What is the rate constant as a function of temperature using Equation (S3-5) and T₀ = 27°C as the base case?

P3-11_B Determine the rate law for the reaction described in each of the cases below involving species A, B, and C. The rate laws should be elementary as written for reactions that are either of the form A → B or A + B → C.

(a) The units of the specific reaction rate are k=[dm3mol⋅h] $k = [\frac{{d m}^{3}}{m o l \cdot h}]$ : Rate Law _________

(b) The units of the specific reaction rate are k=[molkg−cat⋅h(atm)2] $k = [\frac{m o l}{k g - c a t \cdot h {(a t m)}^{2}}]$ : Rate Law _________

(c) The units of the specific reaction rate are k-k=[1h]: $k = [\frac{1}{h}] :$ : Rate Law _________

(d) The units of a nonelementary reaction rate are k=[moldm3⋅h] $k = [\frac{m o l}{{d m}^{3} \cdot h}]$ : Rate Law _________

P3-12_A (a) Write the rate law for the following reactions assuming each reaction follows an elementary rate law. Give the units of k_A for each, keeping in mind some are homogeneous and some reactants are heterogeneous.

The equation reads: Ethylene (C subscript 2 H subscript 4) reacts with half oxygen atom (O subscript 2) to give two singly bonded methylene (CH subscript 2) and in turn, it is single bonded to an oxygen atom in a cyclic manner.

P3-13_A (a) Write the rate law for the reaction

2A + B → C

if the reaction

(1) is second order in B and overall third order, −r_A = _______

(2) is zero order in A and first order in B, −r_A = _______

(3) is zero order in both A and B, −r_A = ______

(4) is first order in A and overall zero order. −r_A = _______

(b) Find and write the rate laws for the following reactions

(1) H₂ + Br₂ → 2HBr

(2) H₂ + I₂ → 2HI

P3-14_B The rate laws for each of the reactions listed below were obtained at low temperatures. The reactions are highly exothermic and therefore reversible at high temperatures. Suggest a rate law for each of the reactions [(a), (b), and (c)] at high temperatures, which may or may not be elementary.

(a) The reaction

A → B

is irreversible at low temperatures and the rate law is

−r_A = KC_A

(b) The reaction

A + 2B → 2D

is irreversible at low temperatures and the rate law is

−r_A = kC_A^l/2C_B

(c) The gas-solid catalyzed reaction

A + B \to c a t C + D

$A + B \underset{c a t}{\to} C + D$

is irreversible at low temperatures and the rate law is

- r A = k P A P B 1 + K A P A + K B P B

$- r_{A} = \frac{k P_{A} P_{B}}{1 + K_{A} P_{A} + K_{B} P_{B}}$

In each case, make sure that the rate laws at high temperatures are thermodynamically consistant at equilibrium (cf. Appendix C).

P3-15_B Solar Chemical Energy Storage. The major ways to utilize, capture, or store the sun’s energy are solar thermal (see P8-16_B), solar voltaic, biomass conversion, solar water splitting (P10-13_B), and solar chemical. Solar chemical refers to processes that harness and store solar energy by adsorbing light in a reversible chemical reaction; see http://en.wikipedia.org/wiki/Solar_chemical. For example, the photodimer-ization of anthracene absorbs and stores solar energy that can be released when the reverse reaction takes place.

Figure P3-15.1 Anthracene dimerization.

Another reaction of interest is the Norbornadiene–Quadricyclane (NQ) couple, where solar energy is adsorbed and stored in one direction and released in the other.

Norbornadiene is converted to quadricyclane by using the solar energy, and the controlled release of the strain energy stored in quadricyclane as it relaxes back to norbornadiene allows the energy to be extracted.

Figure P3-15.2 The Norbornadiene-Quadricyclane (NQ) couple is of potential interest for sunlight energy storage.

(a) Suggest a rate law for the reversible photodimerization of anthracene.

(b) Suggest a rate law for the reversible storage of energy by the NQ couple.

Supplementary Reading

1. Two references relating to the discussion of activation energy have already been cited in this chapter. Activation energy is usually discussed in terms of either collision theory or transition-state theory. A concise and readable account of these two theories may or may not be found in

BURGESS, THORNTON W., The Adventures of Reddy Fox. New York: Dover Publications, Inc., 1913.

LAIDLER, K. J. Chemical Kinetics. New York: Harper & Row, 1987, Chap. 3.

MASEL, R., Chemical Kinetics and Catalysis. New York: Wiley, 2001, p. 594.

2. Prof. Dr. Sven Köttlov of Jofostan University has pointed out that in addition to the books listed above, the rate laws and activation energies can be found in NBS circulars, such as those shown below Table 3-1 on pages 77-78. Also check chemistry literature, e.g., journal of Physical Chemistry. For more on molecular modeling see http://cache.org/teaching−resources-center/molecular-modeling.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 3 Rate Laws

Create new playlist

Sign In

Sign Up

3. Rate Laws

3.1 Basic Definitions

3.1.1 Relative Rates of Reaction

3.2 The Rate Law

3.2.1 Power Law Models and Elementary Rate Laws

3.2.2 Nonelementary Rate Laws

3.2.3 Reversible Reactions

3.3 The Reaction Rate Constant

3.3.1 The Rate Constant k and Its Temperature Dependence

3.3.2 Interpretation of the Activation Energy

Energy changes as we move within the potential energy surfaces.

3.3.3 The Arrhenius Plot

3.4 Molecular Simulations

3.4.1 Historical Perspective

3.4.2 Stochastic Modeling of Reactions7

3.5 Present Status of Our Approach to Reactor Sizing and Design

Summary

CRE Web Site Materials

Questions and Problems

Questions

Computer Simulations and Experiments

Problems

Supplementary Reading

Table of Contents for
Chapter 3 Rate Laws

3.4.2 Stochastic Modeling of Reactions⁷