18. Models for Nonideal Reactors
Success is a journey, not a destination.
—Ben Sweetland
18.1 Some Guidelines for Developing Models
The overall goal is to use the following equation:
By Kinetics we usually mean the rate law and rate-law parameters. The choice of the particular model to be used depends largely on the chemical reaction engineer’s judgment and analysis of the reaction system. It is your job to choose the model that best combines the conflicting goals of mathematical simplicity and physical realism. There is a certain amount of art in the development of a model for a particular reactor, and the examples presented here can only point toward a direction that a chemical reaction engineer’s thinking might follow.
Conflicting goals
A Model must
Fit the data
Be able to extrapolate theory and experiment
Have realistic parameters
For a given real reactor, it is not uncommon to use all the models discussed previously to predict conversion and then make comparisons. Usually, the real conversion will be bounded by the model calculations.
The following guidelines are suggested when developing models for non-ideal reactors:
The model must be mathematically tractable. The equations used to describe a chemical reactor should be solved without an inordinate expenditure of human or computer time.
The model must realistically describe the characteristics of the nonideal reactor. The phenomena occurring in the nonideal reactor must be reasonably described physically, chemically, and mathematically.
The model should not have more than two adjustable parameters. This constraint is often used because an expression with more than two adjustable parameters can be fitted to a great variety of experimental data, and the modeling process in this circumstance is nothing more than an exercise in curve fitting. The statement “Give me four adjustable parameters and I can fit an elephant; give me five and I can include his tail!” is one that I have heard from many colleagues. Unless one is into modern art, a substantially larger number of adjustable parameters is necessary to draw a reasonable-looking elephant.1 A one-parameter model is, of course, superior to a two-parameter model if the one-parameter model is sufficiently realistic. To be fair, however, in complex systems (e.g., internal diffusion and conduction, mass transfer limitations) where other parameters may be measured independently, then more than two parameters are quite acceptable.
1 J. Wei, CHEMTECH, 5, 128 (1975).

Table 18-1 gives some guidelines that will help your analysis and model building of nonideal reaction systems.
The Guidelines
TABLE 18-1 A PROCEDURE FOR CHOOSING A MODEL TO PREDICT THE OUTLET CONCENTRATIONS AND THE CONVERSION
|
When using the algorithm in Table 18-1, we classify a model as being either a one-parameter model (e.g., tanks-in-series model or dispersion model) or a two-parameter model (e.g., reactor with bypassing and dead volume or combi-nations of ideal reactors). In Sections 18.1.1 and 18.1.2, we give an overview of these models, which will be discussed in greater detail later in the chapter.
18.1.1 One-Parameter Models
Here, we use a single parameter to account for the nonideality of our reactor. This parameter is most always evaluated by analyzing the RTD determined from a tracer test.
CSTRs. Examples of one-parameter models for nonideal CSTRs include either a reactor dead volume, VD, where no reaction takes place, or volumetric flow rate with part of the fluid bypassing the reactor, υb, thereby exiting unreacted. Tubular Reactors. Examples of one-parameter models for tubular reactors include the tanks-in-series model and the dispersion model. For the tanks-in-series model, the one parameter is the number of tanks, n, and for the dispersion model, the one parameter is the dispersion coefficient, Da.† Knowing these parameter values, we then proceed to determine the conversion and/or effluent concentrations for the reactor.
† Nomenclature note: Da1 (or Da2) is the Damköhler number and Da is the dispersion coefficient.
Nonideal tubular reactors
First let’s consider nonideal tubular reactors. Tubular reactors may be empty (i.e., no packing), or they may be packed with some material that acts as a catalyst, heat-transfer medium, or means of promoting interphase contact. Until Chapters 16–18, we have modeled the fluid to move through the reactor in a piston-like flow where every atom spends an identical length of time in the reaction environment. Here, the velocity profile is flat, and there is no axial mixing. Both of these assumptions are false, to some extent in every tubular reactor; frequently, they are sufficiently false to warrant some modification of our CRE algorithm. Tubular reactor models need to have the flexibility to allow for failure of the plug-flow assumption and the insignificant axial mixing assumption. Cases where these failures occur include the unpacked laminar-flow tubular reactor, the unpacked turbulent flow reactor, and packed-bed reactors. One of two approaches is usually taken to compensate for failure of either or both of the ideal assumptions. One approach involves modeling the nonideal tubular reactor as a series of identically sized CSTRs, which was discussed in Section 17.4. The other approach (the dispersion model) involves a modification of the ideal reactor by including axial and radial dispersion on the flow and is discussed in this chapter.
18.1.2 Two-Parameter Models
The premise for the two-parameter model is that we can use a combination of ideal reactors to model the real reactor (cf. Section 18.8). For example, consider a packed-bed reactor with channeling and dead zone. Here, the response to a pulse tracer input would show two dispersed pulses in the output as shown in Figure 16-1 and Figure 18-1.
Here, we could model the real reactor as two ideal PBRs in parallel, with the two parameters being the volumetric flow rate that channels or by passes, υb, and the reactor dead volume, VD. The real reactor volume is V = VD + VS with entering volumetric flow rate υ0 = υb + υS.
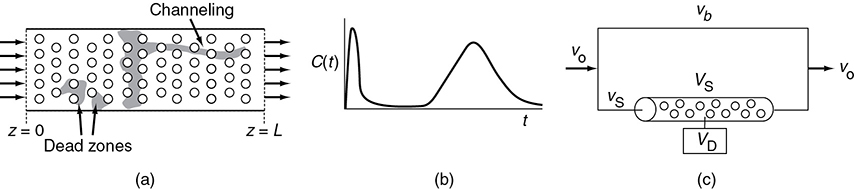
Figure 18-1 (a) Real system; (b) outlet for a pulse input; (c) model system.
18.2 Flow and Axial Dispersion of Inert Tracers in Isothermal Reactors
The dispersion model is also often used to describe nonideal tubular reactors. In this model, there is an axial dispersion of the material, which is governed by an analogy to Fick’s law of diffusion, superimposed on the flow as shown in Figure 18-2. So in addition to transport by bulk flow, UAcC, every component in the mixture is transported through any cross section of the reactor at a rate equal to [–DaAc(dC/dz)] resulting from molecular and convective diffusion. By convective diffusion (i.e., dispersion), we mean either Aris-Taylor dispersion in laminar-flow reactors or turbulent diffusion resulting from turbulent eddies. Radial concentration profiles for plug flow (a) and a representative axial and radial profile for dispersive flow (b) are shown in Figure 18-2. Some molecules will diffuse forward ahead of the molar average velocity, while others will lag behind.
Tracer pulse with dispersion
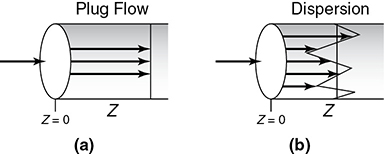
Figure 18-2 Concentration profiles: (a) without and (b) with dispersion.
18.2.1 Balances on Inert Tracers
To illustrate how dispersion affects the concentration profile in a tubular reactor, we consider the injection of a perfect tracer pulse. Figure 18-3 shows how dispersion causes the pulse to broaden as it moves down the reactor and becomes less concentrated.
Why does the tracer pulse broaden?
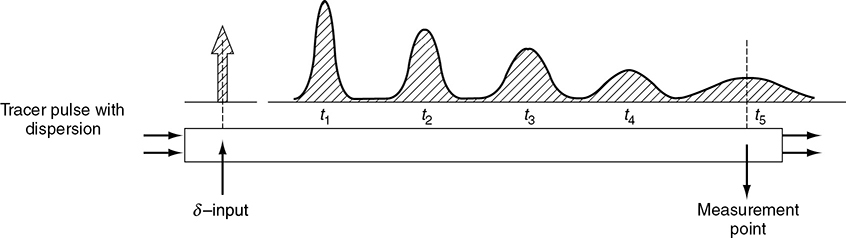
Figure 18-3 Dispersion in a tubular reactor. (Levenspiel, O., Chemical Reaction Engineering, 2nd ed. Copyright © 1972 John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.)
Recall Equation (14-14). The molar flow rate of tracer (FT) by both convection and dispersion is
In this expression, Da is the effective dispersion coefficient (m2/s) and U (m/s) is the superficial velocity. To better understand how the pulse broadens, we refer to the concentration peaks t2 and t3 in Figure 18-4. We see that there is a concentration gradient on both sides of the peak causing molecules to diffuse away from the peak and thus broaden the pulse. The pulse then continues to broaden as it moves through the reactor.
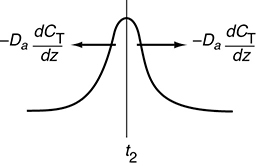
Figure 18-4 Symmetric concentration gradients causing the spreading by dispersion of a pulse input.
Correlations for the dispersion coefficients in both liquid and gas systems may be found in Levenspiel.2 Some of these correlations are given in Section 18.4.
2 O. Levenspiel, Chemical Reaction Engineering. New York: Wiley, 1962, pp. 290–293.
An unsteady-state mole balance on the inert tracer T gives
Substituting for FT and dividing by the cross-sectional area Ac, we have
Pulse tracer balance with dispersion
Letting ψ = CT/CT0 and λ = z/L and Θ = Ut/L can put Equation (18-2) in dimensionless form as
where
Here ℓ is the characteristic length, for example, dp for spherical particle or for the case at hand, L, the length of the reactor. The Péclet number, Per gives a measure of the degree of dispersion. Small Péclet numbers indicate significant dispersion and high Per indicates little dispersion. In the following sections, we will discuss how the dispersion coefficient, Da, and Péclet number can be obtained either from correlations in the literature (cf. Section 18.4) or from the analysis obtained from a tracer experiment on the reactor that yields the RTD curve.
Small Per
High Dispersion
Large Per
Small Dispersion
To solve this equation, we need the initial and boundary conditions. The boundary conditions will now be discussed in detail.
For open tubes
Per ∼ 106,
Pef ∼ 104
For packed beds
Per ∼ 103,
Pef ∼ 101
There are two different types of Péclet numbers in common use. One is the reactor Péclet number, Per: It uses the reactor length, L, for the characteristic length, so Per ≡ UL/Da. It is Per that appears in Equation (18-17). The reactor Péclet number, Per, for mass dispersion is often referred to as the Bodenstein number, Bo, in reacting systems rather than the Péclet number. The other type of Péclet number can be called the fluid Péclet number, Pef; it uses the characteristic length that determines the fluid’s mechanical behavior. In a packed bed, this length is the particle diameter dp, and Pef ≡ Udp/ϕDa. (The term U is the empty tube or superficial velocity. For packed beds, we often wish to use the average interstitial velocity, and thus U/ϕ is commonly used for the packed-bed velocity term.) In an empty tube, the fluid behavior is determined by the tube diameter dt, and Pef = Udt /Da. The fluid Péclet number, Pef, is given in virtually all literature correlations relating the Péclet number to the Reynolds number because both are directly related to the fluid mechanical behavior. It is, of course, very simple to convert Pef to Per: Multiply by the ratio L/dp or L/dt. The reciprocal of Per, Da/UL, is sometimes called the vessel dispersion number.
18.2.2 Boundary Conditions for Flow and Reaction
There are two cases that we need to consider: boundary conditions for closed-closed vessels and for open-open vessels. In the case of closed-closed vessels, we assume that there is no dispersion or radial variation in concentration either upstream (closed) or downstream (closed) of the reaction section; hence, this is a closed-closed vessel, as shown in Figure 18-5(a). In an open-open vessel, dispersion occurs both upstream (open) and downstream (open) of the reaction section; hence, this is an open-open vessel as shown in Figure 18-5(b). These two cases are shown in Figure 18-5, where fluctuations in concentration due to dispersion are superimposed on the plug-flow velocity profile. A closed-open vessel boundary condition is one in which there is no dispersion in the entrance section but there is dispersion in the reaction and exit sections.
Two types of boundary conditions

Figure 18-5 Types of boundary conditions.
18.2.2A Closed-Closed Vessel Boundary Condition
For a closed-closed vessel, we have plug flow (no dispersion) to the immediate left of the entrance line (z = 0–) (closed) and to the immediate right of the exit z = L (z = L+) (closed). However, between z = 0+ and z = L–, we have dispersion and reaction. The corresponding entrance boundary condition for either reactant A or tracer T is
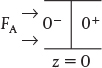
Substituting for FA yields
Solving for the entering concentration CA(0–) = CA0
Concentration boundary conditions at the entrance
At the exit to the reaction section, the concentration is continuous, and there is no gradient in tracer concentration.
Concentration boundary conditions at the exit
At z = L:
Danckwerts boundary conditions
These two boundary conditions, Equations (18-5) and (18-6), first stated by Danckwerts, have become known as the famous Danckwerts boundary conditions.3 Bischoff has given a rigorous derivation by solving the differential equations governing the dispersion of component A in the entrance and exit sections, and taking the limit as the dispersion coefficient, Da in the entrance and exit sections approaches zero.4 From the solutions, he obtained boundary conditions on the reaction section identical with those Danckwerts proposed.
3 P. V. Danckwerts, Chem. Eng. Sci., 2, 1 (1953).
4 K. B. Bischoff, Chem. Eng. Sci., 16, 131 (1961).
The closed-closed concentration boundary condition at the entrance is shown schematically in Figure 18-6. One should not be uncomfortable with the discontinuity in concentration at z = 0 because if you recall for an ideal CSTR, the concentration drops immediately on entering from CA0 to CAexit. For the other boundary condition at the exit z = L, we see the concentration gradient, (dCA/dz), has gone to zero. At steady state, it can be shown that this Danckwerts boundary condition at z = L also applies to the open-open system at steady state.
Closed-Closed Boundary Condition
Figure 18-6 Schematic of Danckwerts boundary conditions: entrance; (b) exit.
Prof. P. V. Danckwerts, Cambridge University, United Kingdom
18.2.2B Open-Open System
For an open-open system, there is continuity of flux at the boundaries at z = 0
FA(0–) = FA(0+)
Open-open boundary condition
At z = L, we have continuity of concentration and
18.3 Flow, Reaction, and Axial Dispersion
Now that we have an intuitive feel for how dispersion affects the transport of molecules in a tubular reactor, we shall consider two types of dispersion in a tubular reactor, laminar and turbulent.
18.3.1 Balance Equations
In Chapter 14, we showed that the mole balance on reacting species A flowing in a tubular reactor was
Rearranging Equation (14-17) we obtain
This equation is a second-order ordinary differential equation. It is nonlinear when rA is other than zero or first order.
When the reaction rate rA is first order, rA = –kCA, then Equation (18-10)
Flow, reaction, and dispersion
is amenable to an analytical solution. However, before obtaining a solution, we put our Equation (18-10) describing dispersion and reaction in dimensionless form by letting ψ = CA/CA0 and λ = z/L
Da = Dispersion coefficient
Da1 = Damköhler number
We recall from Chapter 5 that the quantity Da1 appearing in Equation (18-11) is called the Damköhler number for a first-order conversion and physically represents the ratio
Damköhler number for a first-order reaction
18.3.2 Solution for a Closed-Closed System
We now shall solve the dispersion reaction balance for a first-order reaction
For the closed-closed system, the Danckwerts boundary conditions in dimensionless form are
Da1 = τk
Per = UL/Da
Danckwerts† solved the closed-closed system to give the dimensionless concentration profile as
† Lit cit
Dimensionless concentration profile for dispersion and reaction in a tubular reactor
The conversion profile is
To find the conversion leaving the reactor, X, we simple set λ = 1 to obtain
Nomenclature note:
Da1 is the Damköhler number for a first-order reaction, τk. Da is the dispersion coefficient in cm2/s and Per = UL/Da.
This solution was first obtained by Danckwerts and has been published in many places (e.g., Levenspiel).5,6 With a slight rearrangement of Equation (18-17), we obtain the conversion as a function of Da1 and Per.
5 P. V. Danckwerts, Chem. Eng. Sci., 2, 1 (1953).
6 Levenspiel, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999.

Outside the limited case of a first-order reaction, a numerical solution of the equation is required, and because this is a split-boundary-value problem, for example, conditions given at z = 0 and z = L, an iterative technique is needed. We have to be a little cautious here with conversion defined as [(CA0 – CA)/CA0]. We see that at entrance to the reactor λ = 0, CA is less than CA0 meaning X > 0. This value of X greater than zero is a result of A being dispersed at the entrance, not because of reaction.
To evaluate the exit concentration given by Equation (18-17) or the conversion given by Equation (18-18), we need to know the Damköhler and Péclet numbers. The first-order reaction-rate constant, k, and hence Da1 = τk, can be found using the techniques in Chapter 7. In Section 18.4, we discuss three methods to determine the Péclet number and dispersion coefficient.
Example 18–1 Concentration and Conversion Profiles for Dispersion and Reaction in a Tubular Reactor
A first-order reaction with k = 0.25 min–1 is occurring in a tubular reactor with dispersion where the space time is τ = 5.15 min and the Péclet number is Per = 7.5. In Example 18-2, we will show how to use this tracer data to calculate the Damköler number and Péclet number.
Plot the concentration and conversion profiles for a closed-closed system.
Solution
The dimensionless concentration profile is given by Equation (18-15)
where
The conversion profile is
The Damköhler number for this first-order reaction is
Substituting for q, Da1, and Per, the following concentration profiles can be obtained using Polymath, MatLab, Python, or Wolfram simulations in the Living Example Problem (LEP) on the Web site.
Be sure to use the LEP Sliders to get a full understanding of how the parameters affect the profile.

Figure E18-1.1 shows the concentration profiles for three Péclet numbers. The dimensionless residence time function E(θ) is shown in the upper right-hand corner for the three corresponding Péclet numbers.
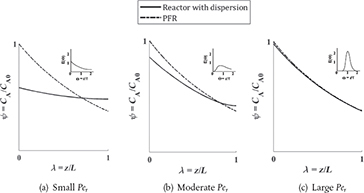
Figure E18-1.1 Concentration profiles for tubular reactor with dispersion.
Analysis: Figure E18-1.1 shows the comparative concentration profiles for a PFR and a reactor with dispersion. For small values of the Péclet number, Figure (a), the dispersion is large and the concentration is distributed throughout the tube and the concentration profiles approach that of a CSTR, one again notes that for a CSTR the entering feed concentration immediately drops form CA0 to CA. For large values of Per, Figure (c), there is virtually no dispersion and the profile approaches that of a PFR. Figure (b) shows the profiles for Péclet numbers in between the extremes of (a) and (c).
As we will see in Example 18-2, the solution to find the exit reactant concentration or the conversion requires both Da and Per which will be discussed in Section 18.5.
18.4 Flow, Reaction, and Axial Dispersion in Isothermal Laminar-Flow Reactors and Finding Meno
Three ways to find Da
Nemo in the Disney movie is a fish, but here our fish Meno is the dispersion coefficient, Da. There are three ways we can use to find Da and hence Per:
Laminar flow with radial and axial molecular diffusion theory
Correlations from the literature for pipes and packed beds
Experimental tracer data

Finding Meno from 1, 2, or 3
At first sight, simple models described by Equation (18-11) appear to have the capability of accounting only for axial mixing effects. It will be shown, however, that this approach can compensate not only for problems caused by axial mixing, but also for those caused by radial mixing and other nonflat velocity profiles.7 These fluctuations in concentration can result from different flow velocities and pathways and from molecular and turbulent diffusion.
7 R. Aris, Proc. R. Soc. (London), A235, 67 (1956).
18.4.1 Determine the Dispersion Coefficient (Da) and the Péclet Number (Per)
Let’s first discuss a qualitative description of how dispersion can occur in a laminar-flow tubular reactor. We know that the axial velocity varies in the radial direction according to the well-known parabolic velocity profile:
where U is the average velocity. For laminar flow, we saw that the RTD function E(t) was given by
In arriving at this distribution E(t), it was assumed that there was no transfer of molecules in the radial direction between streamlines. Consequently, with the aid of Equation (16-47), we know that the molecules on the center streamline (r = 0) exited the reactor at a time t = τ/2, and molecules traveling on the streamline at r = 3R/4 exited the reactor at time
Qualitative description of dispersion
The question now arises: What would happen if some of the molecules traveling on the streamline at r = 3R/4 jumped (i.e., diffused) onto the streamline at r = 0? The answer is that they would exit sooner than if they had stayed on the streamline at r = 3R/4. Analogously, if some of the molecules from the faster streamline at r = 0 jumped (i.e., diffused) onto the streamline at r = 3R/4, they would take a longer time to exit (Figure 18-7). In addition to the molecules diffusing between streamlines, they can also move forward or backward relative to the average fluid velocity by molecular diffusion (Fick’s law). With both axial and radial diffusion occurring, the question arises as to what will be the distribution of residence times when molecules are transported between and along streamlines by diffusion. To answer this question, we will derive an equation for the axial dispersion coefficient, Da, that accounts for the axial and radial diffusion mechanisms. In deriving Da, which is often referred to as the Aris-Taylor dispersion coefficient, we closely follow the development given by Brenner and Edwards.8
8 H. Brenner and D. A. Edwards, Macrotransport Processes. Boston: ButterworthHeinemann, 1993.
Molecules diffusing back and forth between streamlines
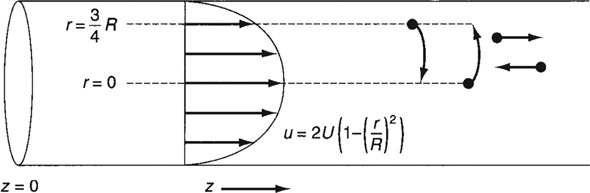
Figure 18-7 Radial diffusion in laminar flow.
The convective–diffusion equation for solute (e.g., tracer) transport in both the axial and radial direction can be obtained by combining Equation (14-2) with the diffusion equation (cf. Equation (14-11)) applied to the tracer concentration, c, and transformed to radial coordinates
where c is the solute concentration at a particular r, z, and t, and DAB is the molecular diffusion coefficient of species A in B.
We are going to change the variable in the axial direction z to z*, which corresponds to an observer moving with the fluid
A value of z* = 0 corresponds to an observer moving with the average velocity of the fluid, U. Using the chain rule, we obtain
Because we want to know the concentrations and conversions at the exit to the reactor, we are really only interested in the average axial concentration, , which is given by

Consequently, we are going to solve Equation (18-21) for the solution concentration as a function of r and then substitute the solution c (r, z, t) into Equation (18-22) to find (z, t). All the intermediate steps are given on the CRE Web site in the Professional Reference Shelf, and the partial differential equation describing the variation of the average axial concentration with time and distance is
where D* is the Aris-Taylor dispersion coefficient
Aris-Taylor dispersion coefficient
That is, for laminar flow in a pipe
Figure 18-8 shows the dispersion coefficient D* in terms of the ratio D* /U(2R) = D* /Udt as a function of the product of the Reynolds (Re) and Schmidt (Sc) numbers.
It was surprising to me how D* could account for both radial and axial dispersion in laminar flow.

Meno! 1.
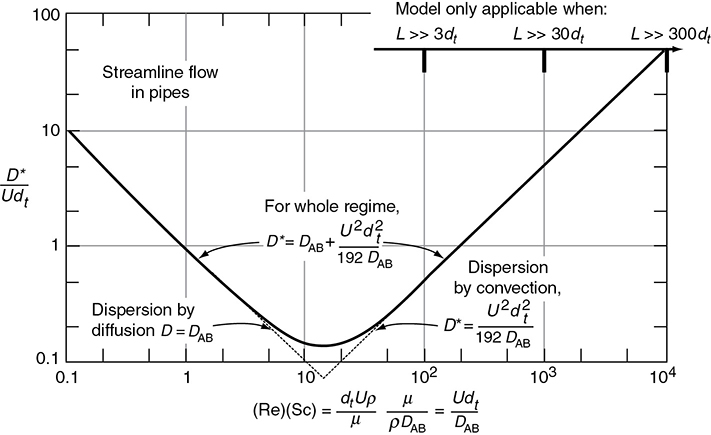
Figure 18-8 Correlation for dispersion for streamline flow in pipes. (Levenspiel, O., Chemical Reaction Engineering, 2nd ed. Copyright © 1972 John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.) Note: D ≡ Da
18.4.2 Correlations for Da
We will use correlations from the literature to determine the dispersion coefficient Da for flow in cylindrical tubes (pipes) and for flow in packed beds.
An estimate of the dispersion coefficient, Da, for laminar and turbulent flow in pipes, can be determined from Figure 18-9. Here, dt is the tube diameter and Sc is the Schmidt number discussed in Chapter 14. The flow is laminar (streamline) below 2,100, and we see the ratio (Da/Udt) increases with increasing Schmidt and Reynolds numbers. Between Reynolds numbers of 2,100 and 30,000, one can put bounds on Da by calculating the maximum and minimum values at the top and bottom of the shaded regions.
1. Meno, i.e., Pe and Da, has been found

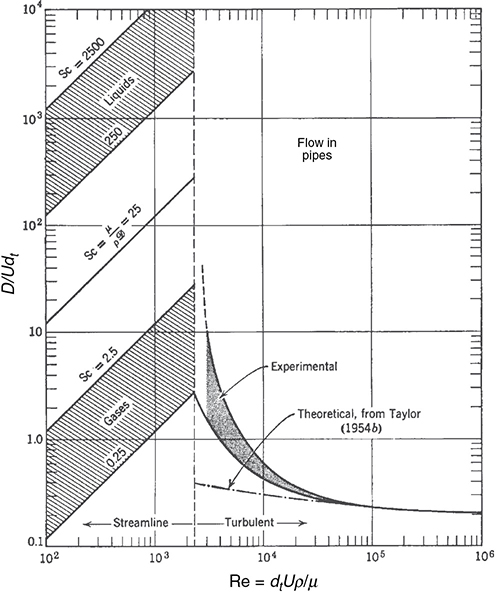
Figure 18-9 Correlation for dispersion of fluids flowing in pipes. (Levenspiel, O., Chemical Reaction Engineering, 2nd ed. Copyright © 1972 John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.) Note: D ≡ Da
18.4.3 Dispersion in Packed Beds
For the case of gas–solid and liquid–solid catalytic reactions that take place in packed-bed reactors, the dispersion coefficient, Da, can be estimated by using Figure 18-10. Here, dp is the particle diameter and ε is the porosity.
18.4.4 Experimental Determination of Da
The dispersion coefficient can be determined from a pulse tracer experiment. Here, we will use tm and σ2 to solve for the dispersion coefficient Da and then
2. Finding Meno in packed beds

Once the Reynolds number is calculated, Da can be found.
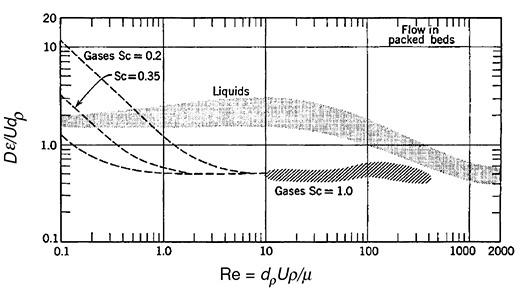
Figure 18-10 Experimental findings on dispersion of fluids flowing with mean axial velocity u in packed beds. (Levenspiel. O., Chemical Reaction Engineering, 2nd ed. Copyright © 1972 John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.) Note: D ≡ Da, ε = void fraction
the Péclet number, Per. Here the effluent concentration of the reactor is measured as a function of time. From the effluent concentration data, the mean residence time, tm, and variance, σ2, are calculated, and these values are then used to determine Da. To show how this is accomplished, we will write the unsteady-state mass balance on the tracer flowing in a tubular reactor
in dimensionless form, discuss the different types of boundary conditions at the reactor entrance and exit, and then solve for the exit concentration as a function of dimensionless time (Θ = t / τ), and then relate Da, σ2, and τ.
18.4.4A What If … Those Correlations Don’t Apply to My Reactors
If I cannot use any of the earlier correlations or graphs, I will just need to find Meno on my own. To do this, I will need to do some theoretical analysis and some experiments to determine the RTD, which we can then analyze to find tm and σ2 and then calculate Da(Per). The first step to find Meno is to put Equation (18-2) in dimensionless form to arrive at the dimensionless group(s) that characterize the process. Again let
![]()
![]()
For a pulse input, CT0 is defined as the mass of tracer injected, M, divided by the vessel volume, V. Then
The initial condition is
Initial condition
The mass of tracer injected, M, is
18.4.4B Solution for a Closed-Closed System
In dimensionless form, the Danckwerts boundary conditions are
Equation (18-3) has been solved numerically for a pulse injection, and the resulting dimensionless effluent tracer concentration at the exit of the reactor, ψexit, is shown as a function of the dimensionless time Θ in Figure 18-11 for various Péclet numbers. Although analytical solutions for ψ can be found, the result is an infinite series. The corresponding equations for the mean residence time, tm, and the variance, σ2, are9
9 See K. Bischoff and O. Levenspiel, Adv. Chem. Eng., 4, 95 (1963).
Effects of dispersion on the effluent tracer concentration

Figure 18-11 C-curves in closed vessels for various extents of back-mixing as predicted by the dispersion model. (Levenspiel, O., Chemical Reaction Engineering, 2nd ed. Copyright © 1972 John Wiley & Sons, Inc. Reprinted by permission of John Wiley & Sons, Inc. All rights reserved.) Note: D ≡ Da10
10 O. Levenspiel, Chemical Reaction Engineering, 2nd ed. New York: Wiley, 1972, p. 277.
and

Meno 3!
which can be used with the solution to Equation (18-3) to obtain
Calculating Per using tm and σ2 determined from RTD data for a closed-closed system
Consequently, we see that the Péclet number, Per (and hence Da), can be found experimentally by determining tm and σ2 from the RTD data and then solving Equation (18-29) for Per.
18.4.4C Solution for Open-Open Vessel Boundary Conditions to Find Meno
When a tracer is injected into a packed bed at a location more than two or three particle diameters downstream from the entrance and measured some distance upstream from the exit, the open-open vessel boundary conditions apply. For an open-open system, an analytical solution to Equation (18-11) can be obtained for a pulse tracer input.
For an open-open system, the boundary conditions at the entrance are
Then, for the case when the dispersion coefficient is the same in the entrance and reaction sections
Open at the entrance
Because there are no discontinuities across the boundary at z = 0
At the exit
Open at the exit
There are a number of perturbations of these boundary conditions that can be applied. The dispersion coefficient can take on different values in each of the three regions (z < 0, 0 ≤ z ≤ and z > L), and the tracer can also be injected at some point z1 rather than at the boundary, z = 0. These cases and others can be found in the supplementary readings cited at the end of this chapter. We shall consider the case when there is no variation in the dispersion coefficient for all z and an impulse of tracer is injected at z = 0 at t = 0.
Again, we let ψ = CA/CA0 and θ = t/τ.
For long tubes (Per > 100) in which the concentration gradient at ±∞ will be zero, the solution to Equation (18-3) giving the dimensionless tracer concentration at the exit is11
11 W. Jost, Diffusion in Solids, Liquids and Gases. New York: Academic Press, 1960, pp. 17, 47.
Valid for Per > 100
The mean residence time for an open-open system is
Calculate τ for an open-open system.
Diffuse in and out.
where τ is based on the volume between z = 0 and z = L (i.e., reactor volume measured with a yardstick). We note that the mean residence time for an open system is greater than that for a closed system. The reason is that the molecules can diffuse out of the reactor at the entrance and then diffuse, or be carried, back into the reactor. The variance for an open-open system is
Calculate Per for an open–open system.
We found Meno 3.

We now consider two cases for which we can use Equations (18-29) and (18-36) to determine the system parameters:
Case 1. The space time τ is known. That is, V and υ0 are measured independently. Here, we can determine the Péclet number by determining tm and σ2 from the concentration–time data and then use Equation (18-36) to calculate Per. We can also calculate tm and then use Equation (18-35) as a check, but this is usually less accurate.
Case 2. The space time τ is unknown. This situation arises when there are dead or stagnant pockets that exist in the reactor along with the dispersion effects. To analyze this situation, we first calculate mean residence time, tm, and the variance, σ2, from the data as in case 1. Then, we use Equation (18-35) to eliminate τ2 from Equation (18-36) to arrive at
Finding the effective reactor voume
We now can solve for the Péclet number in terms of our experimentally determined variables σ2 and . Knowing Per, we can solve Equation (18-35) for τ, and hence V. The dead volume is the difference between the measured volume (i.e., with a yardstick) and the effective volume calculated from the RTD.

Meno 3!
Once we have determined Da and Per from the RTD for our real reactor (i.e., found Meno), we can solve for the conversion from an analytical solution, or for a first-order reaction as in Example 18-1, or solve numerically for other reaction orders.
Example 18–2 Comparing Conversion Using Dispersion, PFR, CSTR, and Tanks-in-Series Models for Isothermal Reactors
The first-order reaction
A → B
is carried out in a 10-cm-diameter tubular reactor 6.36 m in length. The specific reaction rate is 0.25 min–1. The results of a tracer test carried out on this reactor are shown in Table E18-2.1.
TABLE E18-2.1 EFFLUENT TRACER CONCENTRATION AS A FUNCTION OF TIME
t (min) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
14 |
C (mg/L) |
0 |
1.4 |
5 |
8 |
10 |
8 |
6 |
4 |
3 |
2.2 |
1.6 |
0.6 |
0 |
Calculate the conversion using (a) the closed vessel dispersion model, (b) PFR, (c) the tanks-in-series model, and (d) a single CSTR.
Solution
We will use Equation (18-18) to calculate the conversion at the exit
where
(1) Parameter evaluation using the RTD data to evaluate Per:
We can calculate Per from Equation (18-29)
First calculate tm and σ2 from RTD data.
However, we must find τ2 and σ2 from the tracer concentration data first.
Here again, spreadsheets can be used to calculate τ2 and σ2.
TABLE E18-2.2 POLYMATH PROGRAM AND RESULTS TO CALCULATE THE MEAN RESIDENCE TIME, tm, AND THE VARIANCE σ2


Don’t fall asleep. These are calculations we need to know how to carry out.
We note that the data in Table E18-2.1 is the same data set used in Examples 16-1 and 16-2 where we found
and
Are we lucky or what? We will use these values in Equation (18-29) to calculate Per. Dispersion in a closed vessel is represented by
Calculate Per from tm and σ2.
Solving for Per either by trial and error or using Polymath, we obtain
Next, calculate Da1, q, and X.
(2) Next, we calculate Da1 and q:
Using the equations for q and X gives
Then
(3) Finally, we calculate the conversion:
Substitution into Equation (18-18) yields
Dispersion model
When dispersion effects are present in this tubular reactor, 68% conversion is achieved.
(b) If the reactor were operating ideally as a plug-flow reactor, the conversion would be
PFR
That is, 72.5% conversion would be achieved in an ideal plug-flow reactor.
Tanks-in-series model
(c) Conversion using the tanks-in-series model: We recall Equation (17-25) to calculate the number of tanks in series:
To calculate the conversion for the T-I-S model, we recall Equation (5-15). For a first-order reaction for n tanks in series, the conversion is
(d) For a single CSTR
CSTR
So, 56.3% conversion would be achieved in a single ideal tank. Summary:
Summary
In this example, correction for finite dispersion, whether by a dispersion model or a tanks-in-series model, is significant when compared with a PFR.
Analysis: This example is a very important and comprehensive one. We showed how to calculate the conversion by (1) choosing a model, (2) using the RTD to evaluate the model parameters, and (3) substituting the reaction-rate parameters in the chosen model. As expected, the dispersion and T-I-S model gave essentially the same result and this result fell between the limits predicted by an ideal PFR and an ideal CSTR.
18.5 Tanks-in-Series Model versus Dispersion Model
We have seen that we can apply both of these one-parameter models to tubular reactors using the variance of the RTD. For first-order reactions, the two models can be applied with equal ease. However, the tanks-in-series model is mathematically easier to use to obtain the effluent concentration and conversion for reaction orders other than one, and for multiple reactions. However, we need to ask what would be the accuracy of using the tanks-in-series model over the dispersion model. These two models are equivalent when the Péclet–Bodenstein number is related to the number of tanks in series, n, by the equation12
12 K. Elgeti, Chem. Eng. Sci., 51, 5077 (1996).
Equivalency between models of tanks-in-series and dispersion
or
where
where U is the superficial velocity, L the reactor length, and Da the dispersion coefficient.
For the conditions in Example 18-2, we see that the number of tanks calculated from the Bodenstein number, Bo (i.e., Per), Equation (18-39), is 4.75, which is very close to the value of 4.35 calculated from Equation (17-25). Consequently, for reactions other than first order, one would solve successively for the exit concentration and conversion from each tank in series for both a battery of four tanks in series and for five tanks in series in order to bound the expected values.
In addition to the one-parameter models of tanks-in-series and dispersion, many other one-parameter models exist when a combination of ideal reactors is used to model the real reactor shown in Section 18.8 for reactors with bypassing and dead volume. Another example of a one-parameter model would be to model the real reactor as a PFR and a CSTR in series with the one parameter being the fraction of the total volume that behaves as a CSTR. We can dream up many other situations that would alter the behavior of ideal reactors in a way that adequately describes a real reactor. However, it may be that one parameter is not sufficient to yield an adequate comparison between theory and practice. We explore these situations with combinations of ideal reactors in the section on two-parameter models.
The reaction-rate parameters are usually known (e.g., Da), but the Péclet number is usually not known because it depends on the flow and the vessel. Consequently, we need to find Per using one of the three techniques discussed earlier in the chapter.
18.6 Numerical Solutions to Flows with Dispersion and Reaction
We now consider dispersion and reaction in a tubular reactor. We first write our mole balance on species A in cylindrical coordinates by recalling Equation (18-19) and including the rate of formation of A, rA. At steady state we obtain
Analytical solutions to dispersion with reaction can only be obtained for iso-thermal zero- and first-order reactions. We are now going to use COMSOL to solve the flow with reaction and dispersion with reaction.
We are going to compare two solutions: one which uses the Aris-Taylor approach and one in which we numerically solve for both the axial and radial concentration using COMSOL. These solutions are on the CRE Web site.
Case A. Aris-Taylor Analysis for Laminar Flow
For the case of an nth-order reaction, Equation (18-9) becomes
where is the radially averaged axial concentration from r = 0 to r = R, that is,
If we use the Aris-Taylor analysis, we can use Equation (18-9) with a caveat that and λ = z/L we obtain
where
For the closed-closed boundary conditions we have
Danckwerts boundary conditions
For the open-open boundary conditions we have
Equation (18-43) gives the dimensionless concentration profiles for dispersion and reaction in a laminar-flow reactor. For a first-order reaction, we can use Equation (18-26) and (18-27) to obtain the concentration and conversion profiles. For a second-order reaction, the equation becomes nonlinear that needs to be solved numerically. We have used COMSOL in the LEP on the Web site (see http://www.umich.edu/~elements/6e/18chap/expanded_ch18_example2comsol.pdf) to solve for the concentration profiles.
Case B. Full Numerical Solution
To obtain profiles, CA(r, z), we now solve Equation (18-41)
First, we will put the equations in dimensionless form by letting ψ = CA/CA0, λ = z/L, and ϕ = r/R. Following our earlier transformation of variables, Equation (18-46) becomes
Example 18–3 Isothermal Reaction with Radial and Axial Dispersion in an LFR
COMSOL
We now consider flow, reaction and dispersion in cylindrical pipes. The parameter values (e.g., k, U0) will be varied using a COMSOL program. Initially we will use the following values, k = 8.33 × 10–6 m3/mol · s, CA0 = 500 mol/m3, U0 = 0.021 m/s, and DA0 = 1.25 × 10–6 m2/s.
Plot the concentration surface for to and ϕ = 0 to ϕ = 1 and λ = 0 to λ = 1. To make this plot, go to the CRE Web site and load the COMSOL LEP instruction on How to Access COMSOL (http://www.umich.edu/~elements/6e/comsol/comsol_access_instructions.html). Vary the parameters and run the simulation.
Plot the radial concentration profile.
Plot the axial profiles at ϕ = 0 and ϕ = 1/2.
Plot the radially averaged axial concentration profiles CA(z) (i.e., ϕ(λ)).
Solution
The dimensionless form of the equation describing flow, reaction, and dispersion was given in Equation (18-47)
Boundary and Initial Conditions
A. Boundary conditions
Radial
At r = 0, we have symmetry ∂Ci/∂r = 0; in dimensionless form,
There is no mass flow through the tube walls therefore ∂Ci/∂r = 0, at r = R, in dimensionless form
Radially averaged axial concentration is given by
Axial
At the entrance to the reactor z = 0, λ = 0 for all r (i.e., ϕ)
COMSOL
At the exit of the reactor z = L, i.e., λ = 1
#COMSOL
Equation (18-47) and Equations (E18-3.1)–(E18-3.4) were solved using COMSOL. Go to the COMSOL module (http://www.umich.edu/~elements/6e/18chap/obj.html#/comsol/) and run the module and find the following surface plots and profiles. It will really be a great experience for you.
A COMSOL tutorial for this example is given on the Web site in the LEP section for Chapter 18.
The results for a reactor of length 4 m from running the COMSOL simulation are shown in Figure E18-3.1(a), (b), (c), and (d).

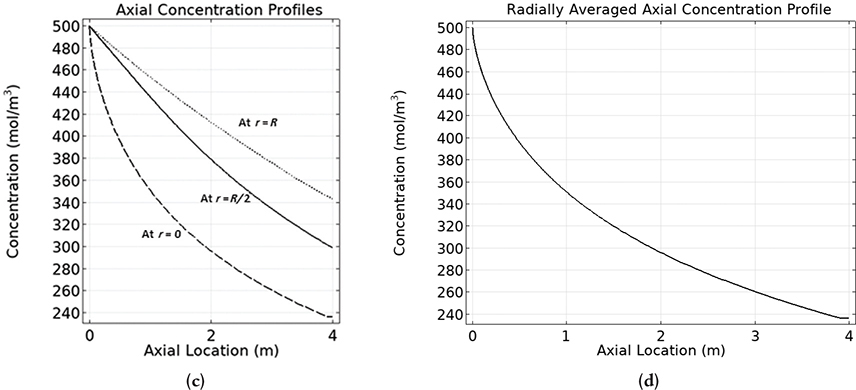
Figure E18-3.1 COMSOL output for laminar flow in the reactor.
In Figure E18-3.1(b) we observe a concentration profiles at the entrance, halfway down the reactor and at the end of the reactor.
Figure E18-3.1(c) shows the axial concentration at different radius while Figure E18-3.1(d) shows the radially averaged axial concentration profile .
Analysis: We observe in Figure E18-3.1(a) and (b) that the concentration profile is flat (plug flow like) at the reactor entrance and then develops into a parabolic shape. This profile shape remains approximately the same from the halfway point until the fluid exits the reactor. In Figure E18-3.1(c) the steepest axial profile was near the wall. One notes the axial profile in Figure E18-3.1(c) is similar to the radial averaged concentration profile shown in Figure E18-3.1(d). Why do you think they are similar?
18.7 Nonisothermal Flow with Radial and Axial Variations in a Tubular Reactor
In the previous sections, we have assumed that there were no radial variations in temperature in the tubular and packed-bed reactors. In this section, we will consider the nonisothermal case where we have both axial and radial variations in the system variables. Here, we will again use COMSOL for solving partial differential equation such as shown in the Radial Effects COMSOL Web Module on the CRE Web site (http://umich.edu/~elements/6e/web_mod/radialeffects/index.htm).13
13 An introductory webinar on COMSOL can be found on the AIChE webinar Web site: http://www.aiche.org/resources/chemeondemand/webinars/modeling-non-ideal-reactors-and-mixers.
COMSOL application
We are going to carry out differential mole and energy balances on the differential cylindrical annulus shown in Figure 18-12.
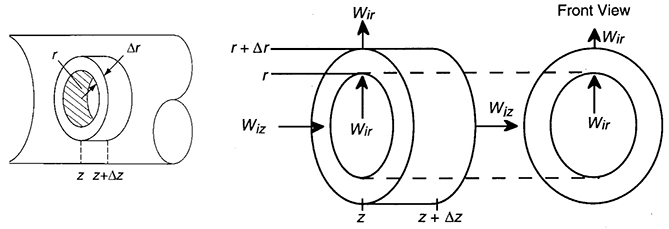
Figure 18-12 Cylindrical shell of thickness Δr, length Δz, and volume 2πrΔrΔz.
18.7.1 Molar Flux
In order to derive the governing equations, we need to define a couple of terms. The first is the molar flux of species i, Wi (mol/m2 · s). The molar flux has two components, the radial component, Wir, and the axial component, Wiz.
The molar flow rates are just the product of the molar fluxes and the cross-sectional areas normal to their direction of flow Acz. For example, for species i flowing in the axial (i.e., z) direction
Fiz = Wiz Acz
where Wiz is the molar flux in the axial z direction (mol/m2/s), and Acz (m2) is the cross-sectional area of the tubular reactor.
In Chapter 14 we discussed the molar fluxes in some detail, but for now let’s just say they consist of a diffusional component, –De(∂Ci/∂z), and a convective-flow component, UzCi, so that the flux Wiz in the axial direction is
where De is the effective diffusivity (or dispersion coefficient) (m2/s), and Uz is the axial molar average velocity (m/s). Similarly, the flux Wir in the radial direction, r, is
Radial direction
where Ur (m/s) is the average velocity in the radial direction. For now, we will neglect the velocity in the radial direction, that is, Ur = 0.
We first recall the mole balance for cylindrical coordinates in Chapter 14.
Using Equations (14-8b) and (18-48) to substitute for Wiz and Wir in Equation (14-2) and then setting the radial velocity to zero, Ur = 0, we obtain
For steady-state conditions and assuming Uz does not vary in the axial direction
18.7.2 Energy Flux
When we applied the first law of thermodynamics to a reactor to relate either temperature and conversion or molar flow rates and concentration, we arrived at Equation (11-10). Neglecting the work term we have for steady-state conditions
In terms of the molar fluxes, Fi = WiAC, the cross-sectional area, AC, and
The q term is the heat added to the system and almost always includes a conduction component of some form. We now define an energy flux vector, e, (J/m2 · s), to include both the conduction and convection of energy.
e = energy flux J/s·m2
e = Conduction + Convection
where the conduction term q (kJ/m2 · s) is given by Fourier’s law. For axial and radial conduction, Fourier’s laws are
where kc is the thermal conductivity (J/m·s·K). The energy transfer (flow) is the flux vector times the cross-sectional area, Ac, normal to the energy flux
Energy flow = e · Ac
18.7.3 Energy Balance
Using the energy flux, e, to carry out an energy balance on our annulus (Figure 12-15) with system volume 2πrΔrΔz, we have
(Energy flow in at r) = er Acr = er · 2πrΔz
(Energy flow in at r) = er Acz = ez · 2πrΔr
Dividing by 2πrΔrΔz and taking the limit as Δr and Δz → 0
The radial and axial energy fluxes are
Substituting for the energy fluxes, er and ez
and expanding the convective energy fluxes, ,
![]()
Because Ur and the gradient in the flux term Wir are small, we can neglect the last term in Equation (18-56) with regard to the other terms in the equation. Substituting Equations (18-56) and (18-57) into Equation (18-55), we obtain upon rearrangement
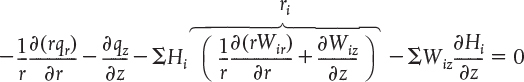
Recognizing that the term in brackets is related to Equation (14-2) and is just the rate of formation of species i, ri, for steady-state conditions we have
Recalling
and
we have the energy in the form
where Wiz is given by Equation (14-8a). Equation (18-59) would be coupled with the mole balance (Equation (18-50)), rate law, and stoichiometric equations to solve for the radial and axial concentration gradients. However, a great amount of computing time would be required. Let’s see if we can make some approximations to simplify the solution.
Some Initial Approximations
Assumption 1. Neglect the diffusive term in the axial direction, wrt, the convective term in Equation (14-8a) in the expression involving heat capacities
With this assumption, Equation (18-59) becomes
For laminar flow, the velocity profile is
where U0 is the average velocity inside the reactor.
Energy balance with radial and axial gradients
Assumption 2. Assume that the sum is constant. The energy balance now becomes
Equation (18-61) is the form we will use in our COMSOL problem. In many instances, the term CPm is just the product of the solution density (kg/m3) and the heat capacity of the solution (kJ/kg · K).
Coolant Balance
We also recall that a balance on the coolant gives the variation of coolant temperature with axial distance where Uht is the overall heat transfer coefficient and R is the reactor wall radius
Boundary and Initial Conditions
A. Initial conditions if other than steady state (not considered here) t = 0, Ci = 0, T = T0, for z > 0 all r
B. Boundary conditions
Radial
At r = 0, we have symmetry ∂T / ∂r = 0 and ∂Ci / ∂r = 0.
At the tube wall, r = R, the temperature flux to the wall on the reaction side equals the convective flux out of the reactor into the shell side of the heat exchanger.
There is no mass flow through the tube walls ∂Ci / ∂r = 0 at r = R
Axial
At the entrance to the reactor z = 0
T = T0 and Ci = Ci0
At the exit of the reactor z = L
The preceding equations were used to describe and analyze flow and reaction in a tubular reactor with heat exchange as described in the following example, which can be found in the Expanded Material on the CRE Web site (http://www.umich.edu/~elements/6e/12chap/expanded.html). What follows is only a brief outline of that example with a few results from the output of the COMSOL program.
Example 18–4 Tubular Reactor with Axial and Radial Temperature and Concentration Gradients
The liquid phase reaction was analyzed using COMSOL to study both axial and radial variations, and the details can be found on the home page of the CRE Web site, www.umich.edu/~elements/6e/index.html, by clicking on the Additional Material for Chapter 18. The algorithm for this example can be found on the Web site: (http://umich.edu/~elements/6e/18chap/expanded_ch18_radial.pdf). Web Figure E12-8.1 is a screen shot from COMSOL of the base case reactor and reaction parameters. In the COMSOL LEP you are asked “What if…” questions about varying the base case parameters. Typical radial (a) and axial (b) temperature profiles for this example are shown in Figure E18-4.1.
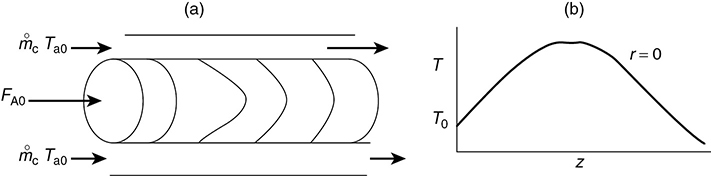
Figure E18-4.1 Radial (a) and axial (b) temperature profiles.
Results. The graphical solutions to the COMSOL code are shown in Figure E18-4.2.
Results of the COMSOL simulation
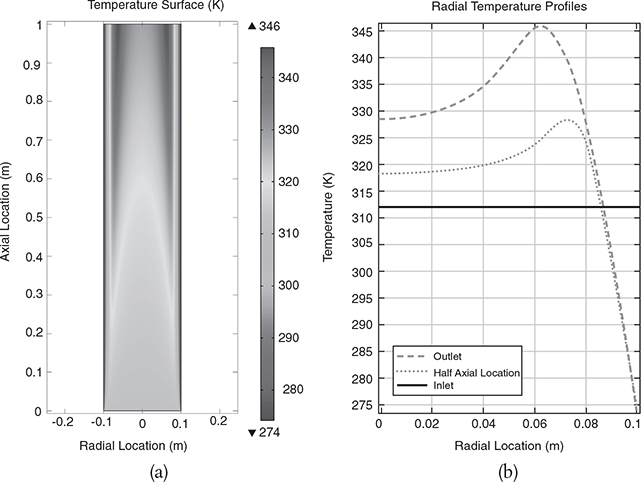
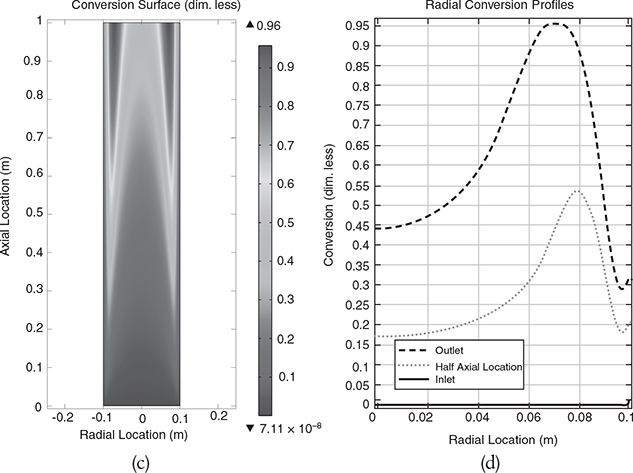
Figure E18-4.2 (a) Temperature surface, (b) temperature surface profiles, (c) conversion surface, and (d) radial profile.
COMSOL
The volumetric flow rate of water is 3.5 times the volumetric flow rate of the mixture of propylene oxide in methanol. Further details of this example are provided in the Chapter 12 Additional Material on the CRE Web site: (http://umich.edu/~elements/6e/software/software_comsol.html).
Analysis: One can observe from the temperature surface plot in Figure E18-4.2(a) how the temperature changes both axially and radially in the reactor from its entering temperature of 312 K. These same profiles can be found in color on the CRE Web site in the Web Modules. Be sure to note the predicted maximum and minimum in the temperature and conversion profiles in Figure E18-4.2(a) to (d). Near the wall, the temperature of the mixture is lower because of the cold wall temperature, which is cooled by the jacket. Consequently, the reaction rate will be lower, and thus the conversion will be lower. However, right next to the wall the flow velocity through the reactor is almost zero, due to the friction with the wall, so the reactants spend a longer time in the reactor; therefore, a greater conversion is achieved, as noted by the upturn right next to the wall.
CRE Web Site—COMSOL
In this interactive Web site and text, you will be able to use the LEP COMSOL program instead of having to write your own code. The CRE LEP COMSOL modules are shown in Figure 18-13. To access these LEPs, you don’t need to have COMSOL installed on your computer as you can access it through the CRE Web site. We use the COMSOL codes in a similar manner to the Polymath LEPs where you are able to vary the parameters to explore the radial variations in temperature, conversion, and concentration, in addition to axial profiles.
COMSOL

Figure 18-13 COMSOL LEP Modules.
18.8 Two-Parameter Models—Modeling Real Reactors with Combinations of Ideal Reactors
Creativity and engineering judgment are necessary for model formulation.
A tracer experiment is used to evaluate the model parameters.
We now will see how a real reactor might be modeled by different combinations of ideal reactors. There are an almost unlimited number of combinations that could be made. However, if we limit the number of adjustable parameters to two (e.g., bypass flow rate, υb, and dead volume, VD), the situation becomes much more tractable. After reviewing the steps in Table 18-1, choose a model and determine whether it is reasonable by qualitatively comparing it with the RTD and, if it is, determine the model parameters. Usually, the simplest means of obtaining the necessary data is some form of a tracer test. These tests have been described in Chapters 16 and 17, together with their uses in determining the RTD of a reactor system. Tracer tests can be used to determine the RTD, which can then be used in a similar manner to determine the suitability of the model and the value of its parameters.
In determining the suitability of a particular reactor model and the parameter values from tracer tests, it may not be necessary to calculate the RTD function E(t). The model parameters (e.g., VD) may be acquired directly from measurements of effluent concentration in a tracer test. The theoretical prediction of the particular tracer test in the chosen model system is compared with the tracer measurements from the real reactor. The parameters in the model are chosen so as to obtain the closest possible agreement between the model and experiment. If the agreement is then sufficiently close, the model is deemed reasonable. If not, another model must be chosen.
What is sufficiently close?
The quality of the agreement necessary to fulfill the criterion “sufficiently close” again depends on creativity in developing the model and on engineering judgment. The most extreme demands are that the maximum error in the prediction not exceed the estimated error in the tracer test, and that there be no observable trends with time in the difference between prediction (the model) and observation (the real reactor). In the Expanded Material on the CRE Web site, we illustrate how the modeling is carried out. We will now consider two different models for a CSTR: first, a CSTR with a dead zone and bypassing; and second, a CSTR model as two CST in interchange. In each of these cases, we will first show how to model the system with two adjustable parameters α and β and then show how to calculate the exit conversion on concentrations.
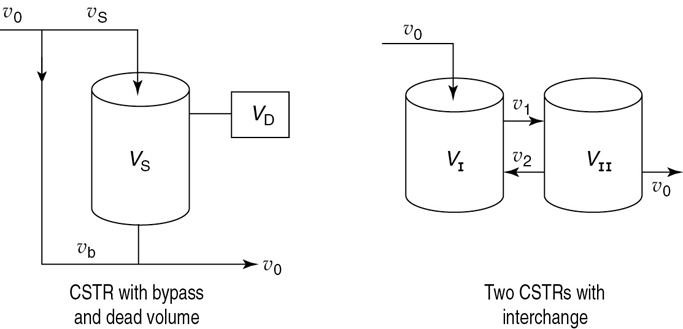
18.8.1 Real CSTR Modeled Using Bypassing and Dead Space
A real CSTR is believed to be modeled as a combination of an ideal CSTR with a well-mixed volume Vs, a dead zone of volume Vd, and a bypass with a volumetric flow rate υb (Figure 18-14). We have used a tracer experiment to evaluate the parameters of the model Vs and υs. Because the total volume and volumetric flow rate are known, once Vs and υs are found, υb and Vd can readily be calculated.
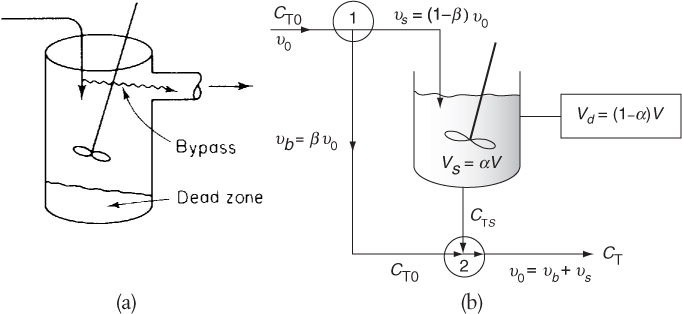
Figure 18-14 (a) Real system; (b) model system.
The model system
18.8.1 A Solving the Model System for CA and X
The bypass stream and effluent stream from the reaction volume are mixed at the junction point 2. From a balance on species A around this point
[In] = [Out]
The Duct Tape Council of Jofostan would like to point out the new wrinkle: The Junction Balance.
In the absence of reaction (e.g., tracer) the concentration exiting the system is
where we will let α = Vs / V and β = υb / υ0.
We will use this model to calculate the conversion for the first-order reaction
A mole balance on the well-mixed volume Vs gives
Mole balance on CSTR
As shown in the extended material on the CRE Web site the exit concentration of species A in terms of α and β
Conversion as a function of model parameters
We have used the ideal reactor system shown in Figure 18-14 to predict the conversion in the real reactor (i.e., Equation (18-66)). The model has two parameters, α and β. The parameter α is the dead zone volume fraction and parameter β is the fraction of the volumetric flow rate that bypasses the reaction zone. If these parameters are known, we can readily predict the conversion. In the following section, we shall see how we can use tracer experiments and RTD data to evaluate the model parameters.
Model system
If we were to inject a positive step tracer into the system shown in Figure 18-14, the unsteady-state tracer balance in a well-mixed reactor value Vs is
In – out = accumulation
Tracer balance for step input
The conditions for the positive-step input are
Solving the tracer balance equations and using a balance around junction point 2, we arrive at the following equation relating CT and t:
Example 18–5 Using a Tracer to Determine the Model Parameters in a CSTR with Dead Space and Bypass Model
The following tracer concentration time data was obtained from a step input to the system in Figure 18-14.
TABLE E18-5.1 TRACER DATA FOR STEP INPUT
CT (mg/dm3) |
1000 |
1333 |
1500 |
1666 |
1750 |
1800 |
t (min) |
4 |
8 |
10 |
14 |
16 |
18 |
The entering tracer concentration is CT0 = 2000 mg/dm3.
Determine the model parameters α and β where α = Vs/V and β = υb/υ0.
Determine the conversion for a second-order reaction with CA0 = 2 kmol/m3, τ = 10 min, and k = 0.28 m3/kmol · min.
Solution
Calculating α and β
The model parameters, α and β, are obtained either by regression (Polymath/ MATLAB/Excel) or from the proper plot of the effluent tracer concentration as a function of time. Rearranging Equation (18-68) yields
Consequently, using Table E18-5.1 we plot ln[CT0/(CT0 = CT)] as a function of t. If our model is correct, a straight line should result with a slope of (1 = β)/τα and an intercept of ln[1/(1 = β)].
TABLE E18-5.2 TRACER DATA FOR STEP INPUT
CT (mg/dm3)
1000
1333
1500
1666
1750
1800
2
3
4
6
8
10
t (min)
4
8
10
14
16
18
When this data is regressed using Equation (E18-5.1), we obtain
Calculating the Conversion
We now can proceed applying our algorithm to this system. A mole balance on reactor Vs gives
For a second-order reaction
The exit concentration is
Substituting parameter values we found that the exit concentration and the conversion predicted in the real (nonideal) reactor are
CA = 0.979 kmol/m3 and
Xmodel = 0.51
XIdeal = 0.66
Using the same rate-law parameter values for or an ideal CSTR we find
CA = 0.685 kmol/m3 and
XIdeal = 0.66
Analysis: In this example we used a combination of an ideal CSTR with a dead volume and bypassing to model a nonideal reactor. If the nonideal reactor behaved as an ideal CSTR, a conversion of 66% was expected. Because of the dead volume, not all the space would be available for reaction; also, some of the fluid did not enter the space where the reaction was taking place and, as a result, the conversion in this nonideal reactor was only 51%.
Other Models. In Section 18.8.1 it was shown how we formulated a model consisting of ideal reactors to represent a real reactor. First, we solved for the exit concentration and conversion for our model system in terms of two parameters, α and β. We next evaluated these parameters from data on tracer concentration as a function of time. Finally, we substituted these parameter values into the mole balance, rate law, and stoichiometric equations to predict the converstion in our real reactor.
To reinforce this concept, we will use one more example (yes, just one more, as given in Example 18-6).
18.8.2 Real CSTR Modeled as Two CSTRs with Interchange
In this particular model there is a highly agitated region in the vicinity of the impeller; outside this region, there is a region with less agitation (Figure 18-15). There is considerable material transfer between the two regions. Both inlet and outlet flow channels connect to the highly agitated region. We shall model the highly agitated region as one CSTR, the quieter region as another CSTR, with material transfer between the two.
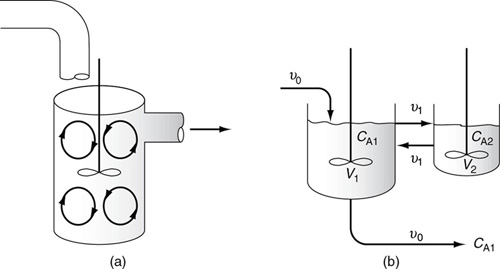
Figure 18-15 (a) Real reaction system; (b) model reaction system.
The model system
18.8.2 A Solving the Model System for CA and X
Let β represent that fraction of the total flow that is exchanged between reactors 1 and 2; υ1 = υ2 = βυ0 and let α represent that fraction of the total volume, V, occupied by the highly agitated region V1 = αV:
The space time is measured as the real reactor volume V divided by the total volumetric flow rate υ0.
As shown on the CRE Web site Professional Reference Shelf R18.2, for a first-order reaction, the exit concentration and conversion are

and
where CA1 is the reactor concentration exiting the first reactor in Figure 18-15(b).
Conversion for two-CSTR model
18.8.2B Using a Tracer to Determine the Model Parameters in a CSTR with an Exchange Volume
The problem now is to evaluate the parameters α and β using the RTD data. CT1 is the measured tracer concentration exiting the real reactor. The tracer is initially dumped only into reactor 1, so that the initial conditions CT10 = NT0/V1 and CT20 = 0.
Using a tracer balance in reactors 1 and 2 in terms of α, β, and τ, we arrive at two coupled differential equations describing the unsteady behavior of the tracer that must be solved simultaneously.
See Appendix A.3 for method of solution.
Analytical solutions to Equations (18-71) and (18-72) are given on the CRE Web site, in Appendix A.3 and in Equation (18-73), below. However, for more complicated systems, analytical solutions to evaluate the system parameters may not be possible.
where
Example 18–6 CSTR with Interchange
A pulse trace test was carried out on the model system shown in Figure 18-15 (http://www.umich.edu/~elements/6e/18chap/Ch18_Web-Additional%20Material.pdf) with , and the results are shown in Table E18-6.1.
TABLE E18-6.1 TRACER DATA FOR PULSE INPUT
t (min) |
0.0 |
20 |
40 |
60 |
80 |
120 |
160 |
200 |
240 |
280 |
320 |
θ = t/τ |
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
C |
2000 |
1050 |
520 |
280 |
160 |
61 |
29 |
16.4 |
10.0 |
6.4 |
4.0 |
C/C10 |
1.0 |
0.525 |
0.26 |
0.14 |
0.08 |
0.03 |
0.0145 |
0.0082 |
0.005 |
0.0032 |
0.002 |
Find the interchange parameters α and β.
Find the conversion for a first-order reaction with k = 0.03 min–1.
Find the corresponding conversion in an ideal CSTR and in an ideal PFR.
Solution
Finding α and β
A pulse tracer experiment is used so that all the tracer, NT0, goes into reactor 1 with volume, V1, that is, (NT0 = C10 V1).
α = V1/V
β = υ1/υ0
A tracer balance yields
(mass added at t = 0) = (mass out over all time)
Solving for α
We see that α is just the area under the curve C(θ) in Figure E18-6.1 divided by C10.
Evaluating the area we obtain
α = 0.80

Figure E18-6.1 Dimensionless tracer concentration as a function of dimensionless time.
As shown on the Web site (http://www.umich.edu/~elements/6e/18chap/Ch18_WebAdditional%20Material.pdf) that by plotting the ratio C(t)/C10 as a function of θ on semi-log coordinates, we get the graph shown on the Web site in Figure Web E18-1.3. At long times, in Equation (18-73) the first term containing m2 in the exponent is negligible with respect to the second term. Consequently, if we extrapolate the portion of the curve for long times back to θ = 0, we have
The values of m1 and m2 are obtained from Figure Web E18-1.3.
Two CSTRs with interchange
Solving for β, we obtain β = 0.1. The two parameters for this model are then
Find the conversion for a first-order reaction
For two CSTRs with interchange, recall Equation (18-70)
Using regression we find
α = 0.8
β = 0.1
We now substitute α, β, τk into Equation (18-70), and as also shown on the CRE Web site, Substituting for τk, α and β in Equation (18-69) yields
Finding conversion in ideal CSTR and ideal PFR
For a single ideal CSTR,
For a single ideal PFR,
Two CSTRs with interchange
Comparing models, we find
(Xmodel = 0.51) < (XCSTR = 0.55) < (XPFR = 0.7)
Analysis: For the two-parameter model chosen, we used the RTD to determine the two parameters’ to find the conversion X, i.e., those parameters were the fraction of the larger fluid volume V1 = αV and the fraction β of fluid exchanged between the reactors, υ1 = βυ0. We next calculated the exit conversion using an ideal CSTR. The CRE algorithm was then applied to model the reactor system where the conversion was found to be 51%, which is smaller than that for an ideal CSTR (x = 0.56).
18.8.3 Other Models of Nonideal Reactors Using CSTRs and PFRs
Several reactor models have been discussed in the preceding pages. All are based on the physical observation that in almost all agitated tank reactors, there is a well-mixed zone in the vicinity of the agitator. This zone is usually represented by a CSTR. The region outside this well-mixed zone may then be modeled in various fashions. We have already considered the simplest models, which have the main CSTR combined with a dead-space volume; if some short-circuiting of the feed to the outlet is suspected, a bypass stream can be added. The next step is to look at all possible combinations that we can use to model a nonideal reactor using only CSTRs, PFRs, dead volume, and bypassing. The rate of transfer between the two reactors is one of the model parameters. The positions of the inlet and outlet to the model reactor system depend on the physical layout of the real reactor.
Figure 18-16(a) describes a real PFR or PBR with channeling that is modeled as two PFRs/PBRs in parallel. The two parameters are the fraction of flow to the reactors (i.e., β and (1 =β)) and the fractional volume (i.e., α and (1 – α)) of each reactor. Figure 18-16(b) describes a real PFR/PBR that has a backmix region and is modeled as a PFR/PBR in parallel with a CSTR. Figures 18-16(a) and (b) on page 973 show a real CSTR modeled as two CSTRs with interchange. In one case, the fluid exits from the top CSTR (a), and in the other case the fluid exits from the bottom CSTR (b). The parameter β represents the interchange volumetric flow rate, βυ0, and = the fractional volume of the top reactor, =V, where the fluid exits the reaction system. We note that the reactor in Figure 18-16(b) was found to describe extremely well a real reactor used in the production of terephthalic acid.14 A number of other combinations of ideal reactions can be found in Levenspiel.15
14 Proc. Indian Inst. Chem. Eng. Golden Jubilee, a Congress, Delhi, 1997, p. 323.
15 Levenspiel, O. Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999, pp. 284–292.
A case history for terephthalic acid
Models for nonideal reactors
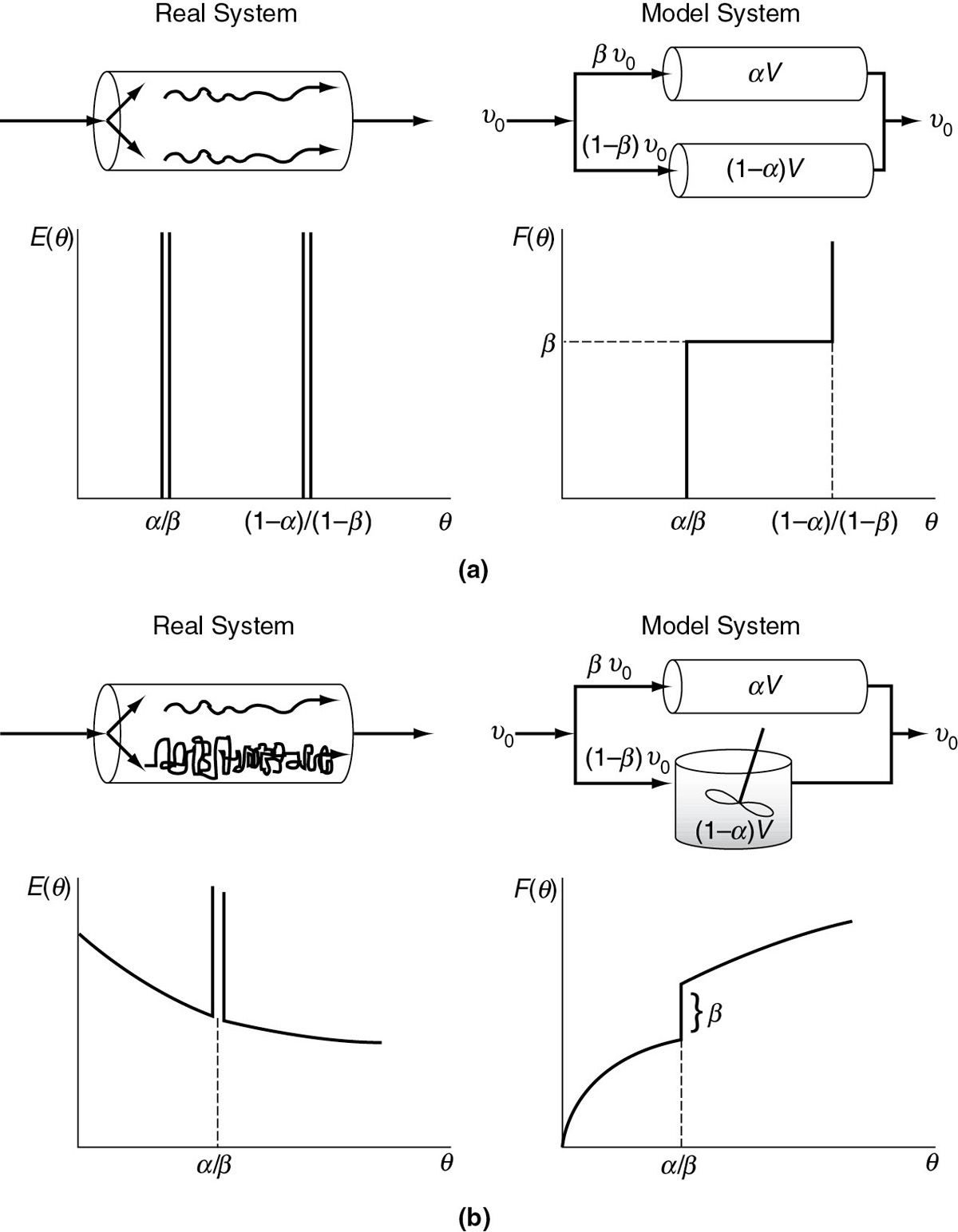
Figure 18-16 Combinations of ideal reactors used to model real tubular reactors: (a) two ideal PFRs in parallel; (b) ideal PFR and ideal CSTR in parallel.
18.8.4 Applications to Pharmacokinetic Modeling
The use of combinations of ideal reactors to model metabolism and drug distribution in the human body is becoming commonplace. For example, one of the simplest models for drug adsorption and elimination is similar to that shown in Figure 18-17(a). The drug is injected intravenously into a central compartment containing the blood (the top reactor). The blood distributes the drug back and forth to the tissue compartment (the bottom reactor) before being eliminated (top reactor). This model will give the familiar linear semi-log plot found in pharmacokinetics textbooks. As can be seen in Chapter 9, in the figure for Professional Reference Shelf R9.8 on the CRE Web site on pharmacokinetics, and on pages 408–409, there are two different slopes, one for the drug distribution phase and one for the elimination phase.

Figure 18-17 Combinations of ideal reactors to model a real CSTR. Two ideal CSTRs with interchange (a) exit from the top of the CSTR; (b) exit from the bottom of the CSTR.
18.9 And Now… A Word from Our Sponsor–Safety 18 (AWFOS–S18 An Algorithm for Management of Change (MoC))
As chemical engineers, it is important for us to understand the aspects of safety involved when we subject a process, plant equipment, or an operating procedure to a change. We must have the ability to look at not only what parameters improve as a result of this change but also at those which may be affected inadvertently and to take proper measures to minimize or at best, nullify the effect of these changes.
We must pay attention to how we define “change.” It is, “anything which is not a like-for-like replacement.”
True Case History
Actual Case History 1: John, Kötloff (Sven’s brother) head of Purchasing at Jofostan Chemical Co. (JCC) was contacted by a new company hoping to sell one of their raw materials to JCC at a cheaper price than their current supplier. They also assured him that they will deliver this highly hazardous liquid to their production facility in the same type of ISO tank (i.e., as per international standards) and with matching connection valves to unload the tank. John went ahead with the purchase without consulting the plant.
Epilogue: The first supply damaged the delivery gantry, because the new supplier used a higher trailer to carry the ISO tank.
Before reading further, let us define risk assessment. Risk assessment is the process of identifying all the possible consequences of an operation and evaluation of their hazards.
Proper and precise description of the change supported with crucial information along with all the paperwork is necessary in order to carry out risk assessment of the change. Before the change is made, the MoC system must identify possible effects and side-effects in order to assess the hazardous consequences and provide a risk assessment of the change.
Actual Case History 2 (Only the names have been changed): In the early 70s, the Jofostan Mixers produced magnesium oxide (MgO) at one of their plants. The MgO was marketed under the name JofoNutri and was added as a nutritional supplement to the feed for dairy cows. The same plant also manufactured polybrominated biphenyls (PBBs) which were used as flame retardant under the name JofoFire.† Sometime in 1973, the paper bags containing JofoFire reached the complex producing dairy feed and was added by the plant operator to the dairy feed assuming that it was JofoNutri.
† M. Venier, A. Salamova, and R. A. Hites, “Halogenated flame retardants in the Great Lakes Environment,” Acc. Chem. Res., 48, 1853–1861 (2015).
Any activity that classifies as a “change” must go through the following, before implemented, as described in the third edition of “Strategies for Creative Problem Solving”:
Make the case for change: identify the need for change and the stake-holders involved.
Vision for change: what will it be like, after the change?
What skills are needed to implement the change as far as design, communication, etc. are concerned?
What is the incentive for the organization to undertake the change?
Do we have enough resources (personnel, knowledge, etc.) to implement the change?
Make an action plan (Gantt chart, timetables, etc.) for the change.
In light of the earlier discussion, answer:
What should a “change” include?
Any definition of change must clearly include changes in equipment, process, or software as well as addition of a new equipment or process. Any modification to organizational structure or any alteration to an operating procedure must also be defined as a change.
What safeguards could have prevented the Jofostan dairy feed incident?
For proper isolation of the harmful chemicals at the facility from the food-grade products, different transport vehicles as well as different personnel should have been employed for JofoNutri and JofoFire.
A distinctive feature on the packaging of all the harmful chemicals at the facility would have allowed operators to distinguish food-grade products from harmful chemicals.
The plant operators should have been sensitive to the presence of harmful chemicals that may be accidentally transported to the dairy feed producing mill.
Use of similar names like JofoNutri and JofoFire should have been avoided as it could have further led to the mix-up.
As the chief of investigation after the Jofostan dairy feed incident, what will be the recommendations of your report to prevent such incidents in the future?
While some of the safeguards in (b) may be recommended, it is important to focus on the “management of change” aspect here.
When the company decided to shift to plain brown bags instead of printed, color-coded bags, it should have flagged this as a “change.”
All stakeholders—Purchasing, Operations, and Logistics—must be notified of this proposal and consulted for their views.
A dedicated safety manager must be entrusted to coordinate with all stake-holders and submit his recommendations before such a proposal goes through. He must evaluate the proposal for change in the manner described earlier.
Summary
The models for predicting conversion from RTD data are:
Zero adjustable parameters
Segregation model
Maximum mixedness model
One adjustable parameter
Tanks-in-series model
Dispersion model
Two adjustable parameters: real reactor modeled as combinations of ideal reactors
Dispersion model: For a first-order reaction, use the Danckwerts boundary conditions
where
For a first-order reaction
Determine Da
For laminar flow, the dispersion coefficient is
Correlations. Use Figures 18-8 through 18-10.
Experiment in RTD analysis to find tm and σ2.
For a closed-closed system, use Equation (S18-5) to calculate Per from the RTD data
For an open-open system, use
If a real reactor is modeled as a combination of ideal reactors, the model should have at most two parameters.
The RTD is used to extract model parameters.
Comparison of conversions for a PFR and CSTR with the zero-parameter and two-parameter models. Xseg symbolizes the conversion obtained from the segregation model and Xmm is that from the maximum mixedness model for reaction orders greater than one.
Cautions: For rate laws with unusual concentration functionalities or for nonisothermal operation, these bounds may not be accurate for certain types of rate laws.
Axial or radial temperature and concentration gradients. The following coupled, partial differential equations were solved using COMSOL:
and
CRE WEB SITE MATERIALS
(http://www.umich.edu/~elements/6e/18chap/obj.html#/)
Useful Links

Evaluation

QUESTIONS, SIMULATIONS, AND PROBLEMS
The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.
A = • B = ■ C = ♦ D = ♦♦
Questions
Q18-1 QBR (Question Before Reading). What if you were asked to design a tubular vessel that would minimize dispersion? What would be your guidelines? How would you maximize the dispersion? How would your design change for a packed bed?
Q18-2B Make up and solve an original problem. The guidelines are given in Problem
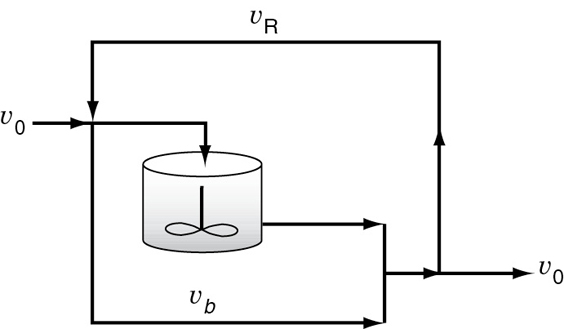
Figure Q18-2 B Model system.

Q18-3A Can you use Figure 18-2 to find the dispersion coefficient for a liquid with a Schmidt number, Sc = 0.35 and a gas porosity ϕ = 0.5, a particle diameter dp = l cm, a gas velocity U = 10 cm/s, and a viscosity of a kinematic υ = 30 cm2/s? If so, what is its value?
Q18-4 What if someone suggested you could use the solution to the flow-dispersion-reactor equation, Equation (18-18), for a second-order equation by linearizing the rate law by lettering Under what circumstances might this be a good approximation? Would you divide CA0 by something other than 2? (2) What do you think of linearizing other non-first-order reactions and using Equation (18-18)? (3) How could you test your results to learn whether the approximation is justified?
Q18-5 Go to the LearnChemE screencast link for Chapter 18 (http://umich.edu/~elements/6e/18chap/learn-cheme-videos.html). View one or more of the screencast 5- to 6-minute videos and write a two-sentence evaluation.
Q18-6 AWFOS–S18. An Algorithm for Management of Change (MoC). List three things that would not have occurred if the MoC algorithm had been followed.
Computer Simulations and Experiments
P18-1b
Example 18-1. Concentration and Conversion Profiles for Dispersion and Reaction in a Tubular Reactor
Wolfram and Python

Vary Péclet number, Per from its largest to smallest value. Describe how the outlet concentration for “reaction with dispersion” deviates from that of “Ideal PFR” as Per is varied.
What should be the minimum value of space time, τ, at which conversion reaches at least 95% for reaction with dispersion.
If the reaction rate constant is increased to 0.5 min–1, what should be the value of Péclet number, Per, so as to achieve conversion of 90%.
Vary the sliders and write a set of conclusions.
Example 18-2. Comparing Conversion Using Dispersion, PFR, CSTR, and Tanks-in-Series Models for Isothermal Reactors
Wolfram and Python
Which parameter will you vary so that conversion obtained by dispersion model approaches to conversion obtained using ideal PFR model.
What is the number of tanks in series required so that conversion obtained by the tank-in-series model is more than conversion obtained by the dispersion model?
Write a set of conclusions after you have varied all the parameter values.
Example 18-3. Isothermal Reaction with Radial and Axial Dispersion in an LFR
Go to the COMSOL link LEP 18-3 in Chapter 18 on the CRE Web site.
Vary the velocity and describe how the radial concentration profiles as well as the surface plot changes.
Vary the reactor radius and describe what you find.
Vary DAB and describe how the radial concentration profiles and the exit concentration change.
Compare the radial concentration profiles at the inlet, exit, and halfway down the reactor with the radially averaged axial concentration when you vary DAB and U and describe what you find.
What combination of parameters, for example, (Da/UL) do not significantly change the base case profile when varied over a wide range? For example, diameter is between 0.01 dm and 1 m and the velocity varies from U = 0.01 cm/s to 1 m/s with DAB = 10–5 cm2/s with υ = μ/ρ = 0.01 m2/s. Is there a diameter that minimizes or maximizes your conversion?
To what parameters or groups of parameters (e.g., kL2/Da) would the conversion be most sensitive? What if the first-order reaction were carried out in tubular reactors of different diameters, but with the space time, τ, remaining constant? The diameters would range from a diameter of 0.1 dm to a diameter of 1 m for a kinematic viscosity υ = μ/ρ = 0.01 cm2/s, U = 0.1 cm/s, and DAB = 10–5 cm2/s. How would your conversion change? Is there a diameter that would maximize or minimize conversion in this range?
Which type of velocity profile gives the higher outlet concentration?
What two parameters would reduce the radial variation in concentration?
Which variable has very little effect on radial variation in concentration?
What is the effect of diffusivity on the outlet concentration?
Keep Da and L/R constant and vary the reaction order n, (0.5 ≤ n ≤ 5) for different Péclet numbers. Are there any combinations of n and Pe where dispersion is more important or less important on the exit concentration? What generalizations can you make? Hint: for n < 1 use .
Write a set of conclusions based on your experiments (i) through (xi).
Example 18-4. Tubular Reactor with Axial and Radial Temperature and Concentration Gradients
Use the COMSOL LEP on the Web site to explore radial effects in a tubular reactor. The Additional Material on the Web site describes this LEP in detail (http://umich.edu/~elements/6e/18chap/expanded_ch18_radial.pdf). Tutorials on how to access and use COMSOL can be found at (http://umich.edu/~elements/6e/software/software_comsol.html).
Vary the heat transfer coefficient, U, and observe the effect on both the conversion and temperature profiles. Why is there an effect of U on the profiles at low values of U, but not at higher values of U?
What is the effect of the different diffusivities, Da, on the conversion? Should Da be minimized or maximized?
What parameter would you vary so that the maximum of the radial conversion profile becomes 1? What is the value of that parameter?
How would your profiles change if the velocity profile was changed to plug flow (U = U0)? Based on your observations, which of the two profiles, namely, laminar flow and plug flow, would you recommend for a larger conversion? How does the change in velocity profile make an effect in the temperature profile?
Intuitively, how do you expect the radial conversion to vary with diffusion coefficient? Explain the reason behind your intuition. Verify this by varying the diffusion coefficient. Investigate axial and radial conversion and write two conclusions.
Example 18-5. Using a Tracer to Determine the Model Parameters in a CSTR with Dead Volume and Bypass Model
Wolfram and Python
For the case of no dead volume (α = 1), vary bypass volume fraction, β, and describe its effect on outlet concentration.
Repeat part (i) for the case of no bypass volume (β = 0) and vary = to observe its effect on outlet concentration.
From your observation in part (i) and part (ii), which of the two model parameters (α or β) have more impact on outlet concentration and conversion? Explain.
Write a set of conclusions based on your experiments in (i) through (iii).
Example 18-6. CSTR with Interchange
Wolfram and Python
For a fixed value of α (say α = 0.5), how does the conversion vary with increase in β? Explain.
Vary α and describe its impact on the exit concentration.
Vary rate constant, k, and describe what you find about its effect on exit concentration.
Write a set of conclusions based on your experiments in (i) through (iii).
Problems
P18-2B The gas-phase isomerization
A → B
is to be carried out in a flow reactor. Experiments were carried out at a volumetric flow rate of υ0 = 2 dm3/min in a reactor that had the following RTD
E(t) = 10 e10t min–1
where t is in minutes.
When the volumetric flow rate was 2 dm3/min, the conversion was 9.1%. What is the reactor volume?
When the volumetric flow rate was 0.2 dm3/min, the conversion was 50%. When the volumetric flow rate was 0.02 dm3/min, the conversion was 91%. Assuming the mixing patterns don’t change as the flow rate changes, what will the conversion be when the volumetric flow rate is 10 dm3/min?
This reaction is now to be carried out in a 1-dm3 plug-flow reactor where volumetric flow rate has been changed to 1 dm3/min. What will be the conversion?
It is proposed to carry out the reaction in a 10-m-diameter pipe where the flow is highly turbulent (Re = 106). There are significant dispersion effects. The superficial gas velocity is 1 m/s. If the pipe is 6 m long, what conversion can be expected? If you were unable to determine the reaction order and the specific reaction-rate constant in part (b), assume k = 1 min–1 and carry out the calculation!
P18-3b OEQ (Old Exam Question). The second-order liquid-phase reaction
A → B + C
is to be carried out isothermally. The entering concentration of A is 1.0 mol/dm3. The specific reaction rate is 1.0 dm3/mol=min. A number of used reactors (shown below) are available, each of which has been characterized by an RTD. There are two crimson and white reactors, and three maize and blue reactors available.
Reactor |
σ(min) |
τ(min) |
Cost |
Maize and blue |
2 |
2 |
$25,000 |
Green and white |
4 |
4 |
50,000 |
Scarlet and gray |
3.05 |
4 |
50,000 |
Orange and blue |
2.31 |
4 |
50,000 |
Purple and white |
5.17 |
4 |
50,000 |
Silver and black |
2.5 |
4 |
50,000 |
Crimson and white |
2.5 |
2 |
25,000 |
You have $50,000 available to spend. What is the greatest conversion you can achieve with the available money and reactors?
How would your answer to (a) change if you had an extra $75,000 available to spend?
From which cities do you think the various used reactors came from?
P18-4B OEQ (Old Exam Question). The elementary liquid-phase reaction
is carried out in a packed-bed reactor in which dispersion is present.
What is the conversion?
Additional information:
Porosity = 50% |
Reactor length = 0.1 m |
Particle size = 0.1 cm |
Mean velocity = 1 cm/s |
Kinematic viscosity = 0.01 cm2/S |
Bed fluidicity = 7.3 |
(Ans: X = 0.15)
P18-5A A gas-phase reaction is being carried out in a 5-cm-diameter tubular reactor that is 2 m in length. The velocity inside the pipe is 2 cm/s. As a very first approximation, the gas properties can be taken as those of air (kinematic viscosity = 0.01 cm2/s), and the diffusivities of the reacting species are approximately 0.005 cm2/s.
How many tanks in series would you suggest to model this reactor?
If the second-order reaction A + B → C + D is carried out for the case of equimolar feed, and with CA0 = 0.01 mol/dm3, what conversion can be expected at a temperature for which k = 25 dm3/mol·s?
How would your answers to parts (a) and (b) change if the fluid velocity was reduced to 0.1 cm/s? Increased to 1 m/s?
How would your answers to parts (a) and (b) change if the superficial velocity was 4 cm/s through a packed bed of 0.2-cm-diameter spheres?
How would your answers to parts (a) through (d) change if the fluid was a liquid with properties similar to water instead of a gas, and the diffusivity was 5 = 10–6 cm2/s?
P18-6A Use the data in Example 16-2 to make the following determinations. (The volumetric feed rate to this reactor was 60 dm3/min.)
Calculate the Péclet numbers for both open and closed systems.
For an open system, determine the space time τ and then calculate the % dead volume in a reactor for which the manufacturer’s specifications give a volume of 420 dm3.
Using the dispersion calculate the conversion for a closed-closed vessel and tanks-in-series models, for the first-order isomerization
A → B
with k = 0.18 min–1.
Compare your results in part (c) with the conversion calculated from the tanks-in-series model, a PFR, and a CSTR.
P18-7A OEQ (Old Exam Question). A tubular reactor has been sized to obtain 98% conversion and to process 0.03 m3/s. The reaction is a first-order irreversible isomerization. The reactor is 3 m long, with a cross-sectional area of 25 dm2. After being built, a pulse tracer test on the reactor gave the following data: tm = 10 s and =2 = 65 s2. What conversion can be expected in the real reactor?
P18-8B The following E(t) curve was obtained from a tracer test on a reactor.
t in minutes, and E(t) in min–1.
The conversion predicted by the tanks-in-series model for the isothermal elementary reaction
A → B
was 50% at 300 K.
If the temperature is to be raised 10°C (E = 25000 cal/mol) and the reaction carried out isothermally, what will be the conversion predicted by the maximum mixedness model? The T-I-S model?
The elementary reactions
were carried out isothermally at 300 K in the same reactor. What is the concentration of B in the exit stream predicted by the maximum mixedness model?
For the multiple reactions given in part (b), what is the conversion of A predicted by the dispersion model in an isothermal closed-closed system?
P18-9B Revisit Problem P16-3C where the RTD function is a hemicircle. The liquid-phase reaction is first order with k1 = 0.8 min–1.
What is the conversion predicted by
The tanks-in-series model? (Ans: XT-I-S = 0.447)
The dispersion model? (Ans: XDispersion = 0.41)
P18-10B Revisit Problem P16-5B. The liquid-phase reaction A → B is third order with k3 = 0.3 dm6/mol2 min and CA0 = 2M.
What combination of ideal reactors would you use to model the RTD?
What are the model parameters?
What is the conversion predicted for your model?
What is the conversion predicted by Xmm, Xseg, XT-I-S, and XDispersion?
Repeat (a) through (d) for a liquid phase reaction A → B is second order with k2 CA0 = 0.1 min–1.
P18-11B Below in Figure P18-11b are two COMSOL simulations for a laminar-flow reactor with heat effects: Run 1 and Run 2. The following figures show the cross-section plot of concentration for species A at the middle of the reactor. Run 2 shows a minimum on the cross-section plot. This minimum could be the result of (circle all that apply and explain your reasoning for each suggestion (a) through (e)).
The thermal conductivity of reaction mixture decreases
Overall heat transfer coefficient increases
Overall heat transfer coefficient decreases
The coolant flow rate increases
The coolant flow rate decreases
Hint: Explore “Nonisothermal Reactor II” on the COMSOL LEP.

Figure P18-11B COMSOL screenshots.
P18-12D Let’s continue Problem P16-11D. Where τ = 10 min and = 14 min2
What would be the conversion for a second-order reaction with kCA0 = 0.1 min–1 and CA0 = 1 mol/dm3 using the segregation model?
What would be the conversion for a second-order reaction with kCA0 = 0.1 min–1 and CA0 = 1 mol/dm3 using the maximum mixedness model?
If the reactor is modeled as tanks in series, how many tanks are needed to represent this reactor? What is the conversion for a first-order reaction with k = 0.1 min–1 ?
If the reactor is modeled by a dispersion model, what are the Péclet numbers for an open system and for a closed system? What is the conversion for a first-order reaction with k = 0.1 min–1 for each case?
Use the dispersion model to estimate the conversion for a second-order reaction with k = 0.1 dm3/mol·s and CA0 = 1 mol/dm3.
It is suspected that the reactor might be behaving as shown in Figure P18-12D, with perhaps (?) V1 = V2. What is the “backflow” from the second to the first vessel, as a multiple of υ0?

Figure P18-12D Proposed model system.
If the model above is correct, what would be the conversion for a second-order reaction with k = 0.1 dm3/mol=min if CA0 = 1.0 mol/dm3?
Prepare a table comparing the conversion predicted by each of the models described above.
P18-13B A second-order reaction is to be carried out in a real reactor that gives the following outlet concentration for a step input:
For 0 ≤ t < 10 min, then CT = 10 (1 –e.1t)
For 10 min ≤ t, then CT = 5 + 10 (1 – e.1t
What model do you propose and what are your model parameters, α and β?
What conversion can be expected in the real reactor?
How would your model change and conversion change if your outlet tracer concentration was as follows?
For t ≤ 10 min, then CT = 0
For t ≥ 10 min, then CT = 5 + 10 (1 –e–0.2(t–10)
υ0 = 1 dm3/min, k = 0.1 dm3/mol · min, CA0 = 1.25 mol/dm3
P18-14b Suggest combinations of ideal reactors to model the real reactors given in Problem P16-2b(b) for either E(θ), E(t), F(θ), F(t), or (1 – F(θ)).
P18-15B OEQ (Old Exam Question). The F-curves for two tubular reactors are shown in Figure P18-15B for a closed-closed system.
Figure P18-15B F-curves.
Which curve has the higher Péclet number? Explain.
Which curve has the higher dispersion coefficient? Explain.
If this F-curve is for the tanks-in-series model applied to two different reactors, which curve has the largest number of T-I-S, (1) or (2)?
U of M, ChE528 Mid-Term Exam
P18-16C Consider the following system in Figure P18-16C used to model a real reactor:
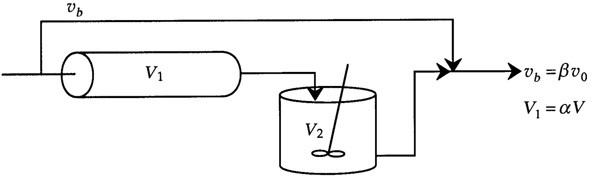
Figure P18-16C Model system.
Describe how you would evaluate the parameters α and β.
Draw the F- and E-curves for this system of ideal reactors used to model a real reactor using β = 0.2 and α = 0.4. Identify the numerical values of the points on the F-curve (e.g., t1) as they relate to τ.
If the reaction A → B is second order with kCA0 = 0.5 min–1, what is the conversion assuming the space time for the real reactor is 2 min?
U of M, ChE528 Final Exam
P18-17B OEQ (Old Exam Question). There is a 2-m3 reactor in storage that is to be used to carry out the liquid-phase second-order reaction
A + B → C
A and B are to be fed in equimolar amounts at a volumetric rate of 1 m3/min. The entering concentration of A is 2 molar, and the specific reaction rate is 1.5 m3/kmol · min. A tracer experiment was carried out and reported in terms of F as a function of time in minutes as shown in Figure P18-17B.
Figure P18-17B F-curve for a nonideal reactor.
Suggest a two-parameter model consistent with the data; evaluate the model parameters and the expected conversion.
U of M, ChE528 Final Exam
P18-18b OEQ (Old Exam Question). The following E-curve shown in Figure P18-18b was obtained from a tracer test:

Figure P18-18B E-curve for a nonideal reactor.
What is the mean residence time?
What is the Péclet number for a closed-closed system?
How many tanks in series are necessary to model this nonideal reactor?
U of M, Doctoral Qualifying Exam (DQE)
P18-19B OEQ (Old Exam Question). A first-order reaction with k = 0.1 min–1 is to be carried out in the reactor whose RTD is shown in Figure 18-19B.
Figure P18-19B Reactor E-curve.
Fill in Table P18-19B with the conversion predicted by each type of model/reactor.
TABLE P18-19B. COMPARISONS OF CONVERSION PREDICTED BY VARIOUS MODELS
Ideal PFR |
Ideal CSTR |
Ideal Laminar-Flow Reactor |
Segregation |
Maximum Mixedness |
Dispersion |
Tanks in Series |
|
|
|
|
|
|
|
P18-20C Consider a real tubular reactor in which dispersion is occurring.
For small deviations from plug flow, show that the conversion for a first-order reaction is given approximately as
Show that to achieve the same conversion, the relationship between the volume of a plug-flow reactor, VP, and volume of a real reactor, V, in which dispersion occurs is
For a Péclet number of 0.1 based on the PFR length, how much bigger than a PFR must the real reactor be to achieve the 99% conversion predicted by the PFR?
For an nth-order reaction, the ratio of exit concentration for reactors of the same length has been suggested as
What do you think of this suggestion?
What is the effect of dispersion on zero-order reactions?
SUPPLEMENTARY READING
Excellent discussions of maximum mixedness can be found in
J. M. DOUGLAS, “The effect of mixing on reactor design,” AIChE Symp. Ser. 48, vol. 60, p. 1 (1964).
TH. N. ZWIETERING, Chem. Eng. Sci., 11, 1 (1959).
Modeling real reactors with a combination of ideal reactors is discussed together with axial dispersion in
O. LEVENSPIEL, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1999.
C. Y. WEN and L. T. FAN, Models for Flow Systems and Chemical Reactors. New York: Marcel Dekker, 1975.
Mixing and its effects on chemical reactor design have been receiving increasingly sophisticated treatment. See, for example:
K. B. BISCHOFF, “Mixing and contacting in chemical reactors,” Ind. Eng. Chem., 58 (11), 18 (1966).
E. B. NAUMAN, “Residence time distributions and micromixing,” Chem. Eng. Commun., 8, 53 (1981).
E. B. NAUMAN and B. A. BUFFHAM, Mixing in Continuous Flow Systems. New York: Wiley, 1983.
See also
M. DUDUKOVIC and R. FELDER, in CHEMI Modules on Chemical Reaction Engineering, vol. 4, ed. B. Crynes and H. S. Fogler. New York: AIChE, 1985.
Dispersion. A discussion of the boundary conditions for closed-closed, open-open, closed-open, and open-closed vessels can be found in
R. ARIS, Chem. Eng. Sci., 9, 266 (1959).
O. LEVENSPIEL and K. B. BISCHOFF, Adv. in Chem. Eng., 4, 95 (1963).
E. B. NAUMAN, Chem. Eng. Commun., 8, 53 (1981).
Now that you have finished this book, suggestions on what to do with the book can be posted on the kiosk in the town square in downtown Riça, Jofostan.
