5. Isothermal Reactor Design: Conversion
Why, a four-year-old child could understand this.
Someone get me a four-year-old child.
—Groucho Marx
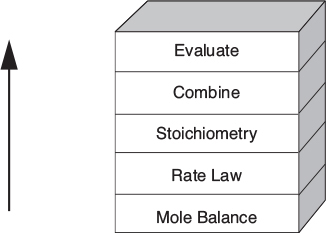
5.1 Design Structure for Isothermal Reactors
One of the primary goals of this chapter is to solve chemical reaction engineering (CRE) problems by using logic rather than memorizing which equation applies where. It is the author’s experience that following this structure, shown in Figure 5-1, will lead to a greater understanding of isothermal reactor design. We begin by applying our general mole balance equation (level ①) to a specific reactor to arrive at the design equation for that reactor (level ②). If the feed conditions are specified (e.g., NA0 or FA0), all that is required to evaluate the design equation is the rate of reaction as a function of conversion at the same conditions as those at which the reactor is to be operated (e.g., temperature and pressure). When –rA = f(X) is known or given, one can go directly from level ③ to the last level, level ⑨, to determine either the batch time or reactor volume necessary to achieve the specified conversion.
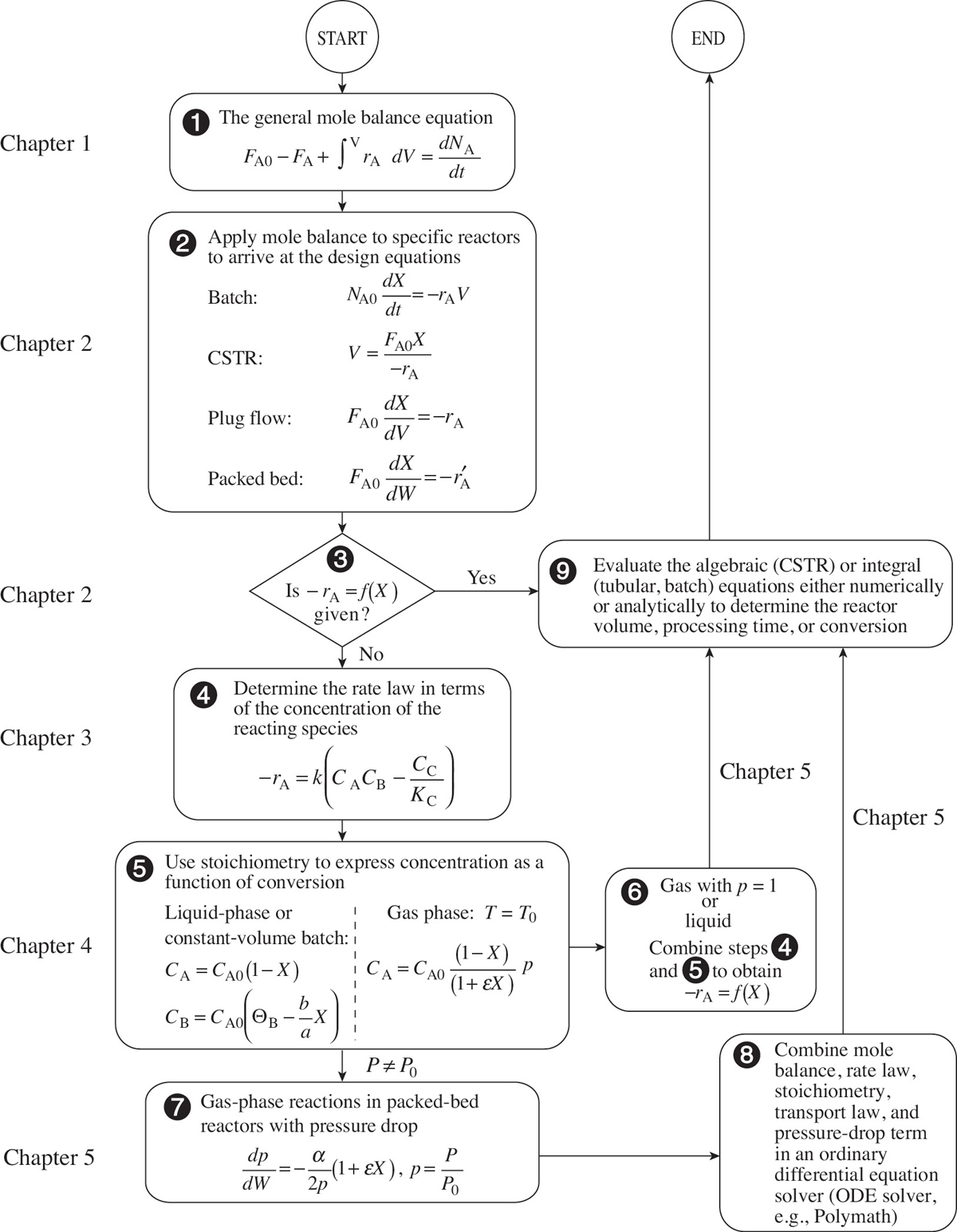
Figure 5-1 Isothermal-reaction design algorithm for conversion.
Logic versus memorization
Use the algorithm rather than memorizing equations.
When the rate of reaction is not given explicitly as a function of conversion, we must proceed to level ④, where the rate law must be determined by either finding it in books or journals or by determining it experimentally in the laboratory. Techniques for obtaining and analyzing rate data to determine the reaction order and rate constant are presented in Chapter 7. After the rate law has been established, one has only to use stoichiometry (level ⑤) together with the conditions of the system (e.g., constant volume, temperature) to express concentration as a function of conversion.
For liquid-phase reactions and for gas-phase reactions with no pressure drop (P = P0), one can combine the information in levels ④ and ⑤ to express the rate of reaction as a function of conversion and arrive at level ⑥. It is now possible to determine either the time or reactor volume necessary to achieve the desired conversion by substituting the relationship linking conversion and rate of reaction into the appropriate design equation (level ⑨).
For gas-phase reactions in packed beds where there is a pressure drop, we need to proceed to level ⑦ to evaluate the pressure ratio p (i.e., (p = P / P0)) in the concentration term using the Ergun equation (Section 5.5). In level ⑧, we combine the equations for pressure drop in level ⑦ with the information in levels ④ and ⑤ to proceed to level ⑨, where the equations are then evaluated in the appropriate manner (i.e., analytically using a table of integrals, or numerically using an ODE solver). Although this structure emphasizes the determination of a reaction time or reactor volume for a specified conversion, it can also readily be used for other types of reactor calculations, such as determining the conversion for a specified volume. Different manipulations can be performed in level ⑨ to answer the different types of questions mentioned here.
The structure shown in Figure 5-1 allows one to develop a few basic concepts and then to arrange the parameters (equations) associated with each concept in a variety of ways. Without such a structure, one is faced with the possibility of choosing or perhaps memorizing the correct equation from a multitude of equations that can arise for a variety of different combinations of reactions, reactors, and sets of conditions. The challenge is to put everything together in an orderly and logical fashion so that we can arrive at the correct equation for a given situation.
Fortunately, by using the algorithm to formulate CRE problems shown in Figure 5-2, which happens to be analogous to the algorithm for ordering dinner from a fixed-price menu in a fine French restaurant, we can eliminate virtually all memorization. In both of these algorithms, we must make choices in each category. For example, in ordering from a Fix Pris French menu,† we begin by choosing one dish from the appetizers listed. Analogous to the French menu, in Step 1 of the CRE algorithm shown in Figure 5-2, we begin by choosing the appropriate mole balance for one of the three types of reactors. After making our reactor choice (e.g., PFR), we go to the small oval ready to make our second choice in Step 2, Rate Laws. In Step 2 we choose the rate law (entrée), and in Step 3 we specify whether the reaction is gas or liquid phase (cheese or dessert). Finally, in Step 4 we combine Steps 1, 2, and 3 and either obtain an analytical solution or solve the equations using an ODE solver.

Figure 5-2 Algorithm for isothermal reactors.
† View the full French menu at (http://www.umich.edu/~elements/6e/05chap/summary-french.html).
The Algorithm
Mole balance
Rate law
Stoichiometry
Combine
Evaluate
We now will apply this algorithm to a specific situation. Suppose that we have, as shown in Figure 5-2, mole balances for three reactors, three rate laws, and the equations for concentrations for both liquid and gas phases. In Figure 5-2, we see how the algorithm is used to formulate the equation to calculate the PFR reactor volume for a first-order gas-phase reaction. The pathway to arrive at this equation is shown by the ovals connected to the dark lines through the algorithm. The dashed lines and the boxes represent other pathways for solutions to other situations. The algorithm for the pathway shown in Figure 5-2 is
Mole balances, choose species A reacting in a PFR
Rate laws, choose the irreversible first-order reaction
Stoichiometry, choose the gas-phase concentration
Combine steps 1, 2, and 3 to arrive at Equation A
Evaluate. The combine step can be evaluated either
Analytically (Appendix A.1)
Graphically (Chapter 2)
Numerically (Appendix A.4)
Via software (e.g., Polymath, Wolfram, Python, MATLAB)
In Figure 5-2, we chose to integrate Equation A for constant temperature and pressure to find the volume necessary to achieve a specified conversion (or calculate the conversion that can be achieved in a specified reactor volume). Unless the parameter values are zero, we typically do not (please trust me when I say do not) substitute numerical values for parameters in the combine step until the very end, that is Step 5 Evaluate.
Substitute parameter values in Steps 1–4 only if they are zero.
For the case of isothermal operation with no pressure drop, we were able to obtain an analytical solution, given by Equation B in Figure 5-2, which gives the reactor volume necessary to achieve a conversion X for a first-order gas-phase reaction carried out isothermally in a PFR. However, in the majority of situations, analytical solutions to the ordinary differential equations appearing in the combine step are not possible. Consequently, we include Polymath, or some other ODE solver such as MATLAB, Wolfram, or Python in our menu in that it makes obtaining solutions to the differential equations much more palatable.
We can solve the equations in the combine step either
Analytically (Appendix A.1)
Graphically (Chapter 2)
Numerically (Appendix A.4)
Using software (e.g., Polymath).
5.2 Batch Reactors (BRs)
One of the jobs in which chemical engineers are involved is the scale-up of laboratory experiments to pilot-plant operation or to full-scale production. In the past, a pilot plant would be designed based on laboratory data. In this section, we show how to analyze a laboratory-scale batch reactor in which a liquid-phase reaction of known order is being carried out.
In modeling a batch reactor, we assume there is no inflow or outflow of material and that the reactor is well mixed. For most liquid-phase reactions, the density change with reaction is usually small and can be neglected (i.e., V = V0). In addition, for gas-phase reactions in which the batch reactor volume remains constant, we also have V = V0.

Figure 5-3 Batch reactor.
(http://encyclopedia.che.engin.umich.edu/Pages/Reactors/Batch/Batch.html)
5.2.1 Batch Reaction Times
The time necessary to achieve a specific conversion depends on how fast the reaction takes place, which in turn is dependent on the rate constant and the reactant concentrations. To get a feel of how long it takes to carry a batch reaction, we shall calculate the batch reaction times for different values of the reaction rate constant, k, for a first- and second-order reaction. First, let’s solve for the time to achieve a conversion X for the second-order reaction:
2A → B + C

The Algorithm
The mole balance on a constant-volume, V = V0, batch reactor is
Mole Balance
Dividing by NA0 and recognizing CA0 = NA0/V0 we obtain
The rate law is
Rate Law
From stoichiometry for a constant-volume batch reactor, we obtain
Stoichiometry
Combining the mole balance, rate law, and stoichiometry we obtain
Next, we substitute for –rA in Equation (5-1)
Combine
To evaluate, we separate the variables and integrate
Initially, if t = 0, then X = 0. If the reaction is carried out isothermally, k will be constant; we can integrate this equation (see Appendix A.1 for a table of integrals used in CRE applications) to obtain
Evaluate
Second-order, isothermal, constant-volume batch reactor
This time is the reaction time t (i.e., tR) needed to achieve a conversion X for a second-order reaction in a batch reactor. In a similar fashion, we can apply the CRE algorithm to a first-order reaction to obtain the reaction time, tR, needed to achieve a conversion X
First-order isothermal constant-volume batch reactor
It is important to have a grasp of the order of magnitudes of batch reaction times, tR, to achieve a given conversion, say 90%, for different values of the product of specific reaction rate, k, and initial concentration, CA0. Table 5-1 shows the algorithm to find the batch reaction times, tR, for both first- and second-order reactions carried out isothermally. We can obtain these estimates of tR by considering the first- and second-order irreversible reactions of the form
2A → B + C
TABLE 5-1 ALGORITHM TO ESTIMATE REACTION TIMES
Mole Balance |
|
||
Rate Law |
First-Order –rA = k1CA |
Second-Order
|
|
Stoichiometry (V = V0) |
|
||
Combine |
|
|
|
Evaluate (Integrate) |
|
|
Constant Volume V = V0
For first-order reactions, the reaction time to reach 90% conversion (i.e., X = 0.9) in a constant-volume batch reactor scales as
If k1 = 10–4 s–1,
The time necessary to achieve 90% conversion in a batch reactor for an irreversible first-order reaction in which the specific reaction rate, k1, is (10–4 s–1) is 6.4 h.
For second-order reactions, we have
If k2CA0 = 10–3 s–1,
We note that if 99% conversion had been required for this value of kCA0, the reaction time, tR, would jump to 27.5 h.
Table 5-2 gives the order of magnitude of time to achieve 90% conversion for first- and second-order irreversible batch reactions. Flow reactors would be used for reactions with characteristic reaction times, tR, of minutes or less.
TABLE 5-2 BATCH REACTION TIMES
First-Order k1 (s–1) |
Second-Order k2CA0 (s–1) |
Reaction Time tR |
10–4 |
10–3 |
Hours |
10–2 |
10–1 |
Minutes |
1 |
10 |
Seconds |
1000 |
10000 |
Milliseconds |

Estimating reaction times
The times in Table 5-2 are the reaction time to achieve 90% conversion (i.e., to reduce the concentration from CA0 to 0.1 CA0). The total cycle time in any batch operation is often, considerably longer than the reaction time, tR, as one must account for the time necessary to fill (tf) and heat (te) the reactor together with the time necessary to clean the reactor between batches, tc. In some cases, the reaction time calculated from Equations (5-4) and (5-5) may be only a small fraction of the total cycle time, tt.
tt = tf + te + tc + tR
Typical cycle times for a batch polymerization process are shown in Table 5-3. Batch polymerization reaction times, tR, may vary between 5 and 60 hours. Clearly, decreasing the reaction time with a 24-hour reaction, as is the case in Example 13-2, is a promising endeavor. As the reaction time is reduced (e.g., 2.5 hours for a second-order reaction with k2CA0 = 10–3 s–1), it becomes important to use large lines and pumps to achieve rapid transfers and to utilize efficient sequencing to minimize the cycle time.
TABLE 5-3 TYPICAL CYCLE TIME FOR A BATCH POLYMERIZATION PROCESS
Activity |
Time (h) |
1. Charge feed to the reactor and agitate, tf |
0.5–2.0 |
2. Heat to reaction temperature, te |
0.5–2.0 |
3. Carry out reaction, tR |
(varies) |
4. Empty and clean reactor, tc |
1.5–3.0 |
______ |
|
Total time excluding reaction |
2.5–7.0 |
Batch operation times
Usually, one has to optimize the reaction time with the processing times listed in Table 5-3 to produce the maximum number of batches (i.e., pounds or kilograms of product) in a day.
In the next four examples, we will describe the various reactors needed to produce 200 million pounds per year of ethylene glycol from a feedstock of ethane. We begin by finding the rate constant, k, for the hydrolysis of ethylene oxide to form ethylene glycol.
Example 5–1 Determining k from Batch Data
It is desired to design a CSTR to produce 200 million pounds of ethylene glycol per year by hydrolyzing ethylene oxide. However, before the design can be carried out, it is necessary to perform and analyze a batch-reactor experiment to determine the specific reaction-rate constant, k. Because the reaction will be carried out isothermally, the specific reaction rate will need to be determined only at the reaction temperature of the CSTR. At temperatures above 80°C, there is a significant by-product formation, while at temperatures below 40°C, the reaction does not proceed at a significant rate; consequently, a temperature of 55°C has been chosen. Because water is present in excess, its concentration (55.5 mol/dm3) may be considered constant during the course of the reaction. The reaction is first-order in ethylene oxide.


Ethylene Oxide
In the laboratory experiment, 500 mL of a 2 M solution (2 kmol/m3) of ethylene oxide (A) in water was mixed with 500 mL of water (B) containing 0.9 wt % sulfuric acid, which is a catalyst. The temperature was maintained at 55°C. The concentration of ethylene glycol (C) was recorded as a function of time (Table E5-1.1).
Derive an equation for the concentration of ethylene glycol as a function of time.
Rearrange the equation derived in (a) to obtain a linear plot of a function concentration versus time.
Using the data in Table E5-1.1, determine the specific reaction rate, k, at 55°C.
TABLE E5-1.1 CONCENTRATION–TIME DATA
Time (min) |
Concentration of Ethylene Glycol (C) (kmol/m3)* |
0.0 |
0.000 |
0.5 |
0.145 |
1.0 |
0.270 |
1.5 |
0.376 |
2.0 |
0.467 |
3.0 |
0.610 |
4.0 |
0.715 |
6.0 |
0.848 |
10.0 |
0.957 |
*1 kmol/m3 = 1 mol/dm3 = 1 mol/L.

Ethylene Glycol

Check 10 types of homework problems on the CRE Web site for more solved examples using this algorithm. (http://www.umich.edu/~elements/6e/probsolv/tentypes/index.htm)
Solution
Part (a)
The mole balance on ethylene oxide (A) given in Equation (1-5) for a constant volume, V0, well-mixed batch reactor can be written as

Taking V0 inside the differential and recalling that the concentration is
then the differential mole balance becomes

The rate law for the ethylene oxide hydrolysis is

Because water is present in such excess, the concentration of water at any time t is virtually the same as the initial concentration, and the rate law is independent of the concentration of H2O (CB ≅ CB0 = 55.5 moles per dm3).†
† The reaction is actually pseudo first order because B is in excess so that –rA = k2CACB ≅ k2CB0CA = kCA where k = k2CB0.
Stoichiometry. Liquid phase, no volume change, V = V0 (Table E5-1.2):
TABLE E5-1.2 STOICHIOMETRIC TABLE
Species
Symbol
Initial
Change
Remaining
Concentration
CH2 CH2O
A
NA0
–NA0X
NA = NA0(1 – X)
CA = CA0(1 – X)
H2O
B
ΘBNA0
–NA0X
NB = NA0(ΘB – X)
CB = CA0(ΘB – X)
CB ≈ CA0ΘB = CB0
(CH2OH)2
C
0
NA0X
NC = NA0X
CC = CA0X = CA0 – CA
NT0
NT = NT0 – NA0X

Recall that ΘB is the ratio of the initial number of moles of B to moles of A (i.e., ).
For species B, that is, water,
CB = CA0(ΘB – X)
We quickly see that water is in excess, as the molarity of water is 55 moles per liter. The initial concentration of A after mixing the two volumes together is 1 molar. Therefore,
The maximum value of X is 1, and ΘB >>1, therefore CB is virtually constant
CB ≅ CA0 ΘB = CB0
For species C, that is, ethylene glycol, the concentration is
Combining the rate law and the mole balance, we have
Evaluate. For isothermal operation, k is constant, so we can integrate this equation (E5-1.5)
Combining mole balance, rate law, and stoichiometry
using the initial condition that
when t = 0, then CA = CA0 = 1 mol/dm3 = 1 kmol/m3.
Integrating yields
The concentration of ethylene oxide (A) at any time t is
The concentration of ethylene glycol (C) at any time t can be obtained from the reaction stoichiometry, that is, Equation (E5-1.4)

Part (b)
We are now going to rearrange Equation (E5-1.8) for the concentration of ethylene glycol in such a manner that we can easily use the data in Table E5-1.1 to determine the rate constant k. Rearranging Equation (E5-1.8) to
then dividing by CA0 and taking the natural log of both sides of Equation (E5-1.9) one obtains
Part (c)
We see that a plot of ln[(CA0 – CC)/CA0] as a function of t will be a straight line with a slope –k. Using Table E5-1.1, we can construct Table E5-1.3 and use Excel to plot ln(CA0 – CC)/CA0 as a function of t.
TABLE E5-1.3 PROCESSED DATA
t (min) |
CC (kmol/m3) |
||
0.0 |
0.000 |
1.000 |
0.0000 |
0.5 |
0.145 |
0.855 |
–0.1570 |
1.0 |
0.270 |
0.730 |
–0.3150 |
1.5 |
0.376 |
0.624 |
–0.4720 |
2.0 |
0.467 |
0.533 |
–0.6290 |
3.0 |
0.610 |
0.390 |
–0.9420 |
4.0 |
0.715 |
0.285 |
–1.2550 |
6.0 |
0.848 |
0.152 |
–1.8840 |
10.0 |
0.957 |
0.043 |
–3.1470 |
From the slope of a plot of ln[(CA0 – CC)/CA0] versus t, we can find k, as shown in the Excel plot in Figure E5-1.1.

Figure E5-1.1 Excel plot of data.
Evaluating the specific reaction rate from batch-reactor concentration– time data
Slope = –k = –0.311 min–1
k = 0.311 min–1
The rate law becomes
The rate law can now be used in the design of an industrial CSTR. For those who prefer to find k using semi-log graph paper, this type of analysis can be found at www.physics.uoguelph.ca/tutorials/GLP. Tutorials are also given in the Summary Notes for Chapter 3 (last example) and Chapter 7 (Excel).

Analysis: In this example, we used our CRE algorithm
(mole balance → rate law → stoichiometry → combine)
to calculate the concentration of species C, CC, as a function of time, t. We then used experimental batch data of CC versus t to verify the reaction as a pseudo first-order reaction and to determine the pseudo first-order specific reaction-rate constant, k (s–1).
5.3 Continuous-Stirred Tank Reactors (CSTRs)
Continuous-stirred tank reactors (CSTRs), such as the one shown here schematically in Figure 5-4, are typically used for liquid-phase reactions.
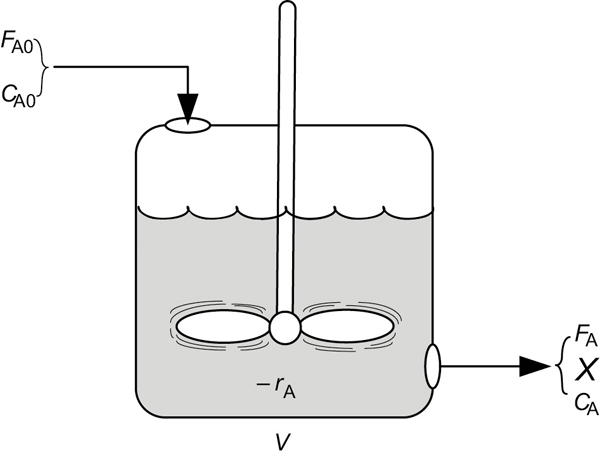
Figure 5-4 CSTR.
(http://encyclopedia.che.engin.umich.edu/Pages/Reactors/CSTR/CSTR.html)
In Chapter 2, we derived the following design equation for a CSTR
Mole Balance
which gives the volume V necessary to achieve a conversion X. As we saw in Chapter 2, the space time, τ, is a characteristic time of a reactor. To obtain the space time, τ, as a function of conversion, we first substitute for FA0 = υ0CA0 in Equation (2-13)
and then divide by υ0 to obtain the space time, τ, to achieve a conversion X in a CSTR
This equation applies to a single CSTR or to the first reactor of CSTRs connected in series.
5.3.1 A Single CSTR
5.3.1.1 First-Order Reaction in a CSTR
Let’s consider a first-order irreversible reaction for which the rate law is
–rA = kCA
Rate Law
For liquid-phase reactions, there is no volume change during the course of the reaction, so we can use Equation (4-12) to relate concentration and conversion
Stoichiometry
We can combine the mole balance equation (5-7), the rate law, and the concentration equation (4-12) to obtain
Combine
Rearranging
CSTR relationship between space time and conversion for a first-order liquid-phase reaction
A plot of conversion as a function of τk using Equation (5-8) is shown in Figure 5-5.

Figure 5-5 First-order reaction in a CSTR.
We can increase τk by either increasing the temperature to increase k or increasing the space time τ by increasing the volume V or decreasing the volu-metric flow rate υ0. For example, when we increase the reactor volume, V, by a factor of 2 (or decrease the volumetric flow rate υ0 by a factor of 2) as we go from τk = 4 to τk = 8, the conversion only increases from 0.8 to 0.89. Do you think it is worth the additional cost of a larger reactor to increase the conversion by only 0.09 or can you think of a better way to increase τk or the conversion?
We could also combine Equations (4-12) and (5-8) to find the exit reactor concentration of A, CA,
5.3.1.2 A Second-Order Reaction in a CSTR
For an irreversible second-order liquid-phase reaction, for example,
being carried out in a CSTR, the combination of the second-order rate law and the design equation (i.e., combined mole balance Equation (2-13) and rate law) yields
Using our stoichiometric table for constant density υ = υ0, CA = CA0(1 – X), and FA0 X = υ0 CA0X, then
Dividing both sides of the combined rate law and design equation for a second-order reaction by υ0 gives
We solve Equation (5-10) for the conversion X
Conversion for a second-order liquid-phase reaction in a CSTR
The minus sign must be chosen in the quadratic equation because X cannot be greater than 1. Conversion is plotted as a function of the Damköhler parameter for a second-order reaction, Da2 = τkCA0, in Figure 5-6. Observe from this figure that at high conversions (say 67%), a 10-fold increase in the reactor volume (or increase in the specific reaction rate by raising the temperature) will only increase the conversion up to 88%. This observation is a consequence of the fact that the CSTR operates under the condition of the lowest reactant concentration (i.e., the exit concentration), and consequently the smallest value of the rate of reaction.
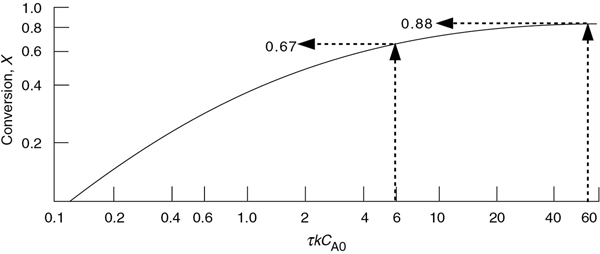
Figure 5-6 Conversion as a function of the Damköhler number (Da2 = τkCA0) for a second-order reaction in a CSTR.
5.3.1.3 The Damköhler Number
For a first-order reaction, the product τk is often referred to as the reaction Damköhler number, Da1, which is a dimensionless number that can give us a quick estimate of the degree of conversion that can be achieved in continuous-flow reactors. The Damköhler number is the ratio of the rate of reaction of A to the rate of convective transport of A evaluated at the entrance to the reactor.
The Damköhler number for a first-order irreversible reaction is
The Damköhler number for a second-order irreversible reaction is
It is important to know what values of the Damköhler number, Da, give high and low conversion in continuous-flow reactors. For irreversible reactions, a value of Da = 0.1 or less will usually give less than 10% conversion, and a value of Da = 10.0 or greater will usually give greater than 90% conversion; that is, the rule of thumb is
0.1 ≤ Da ≤ 10

Equation (5-8) for a first-order liquid-phase reaction in a CSTR can also be written in terms of the Damköhler number
5.3.2 CSTRs in Series
A first-order reaction with no change in the volumetric flow rate (υ = υ0) is to be carried out in two CSTRs placed in series (Figure 5-7).
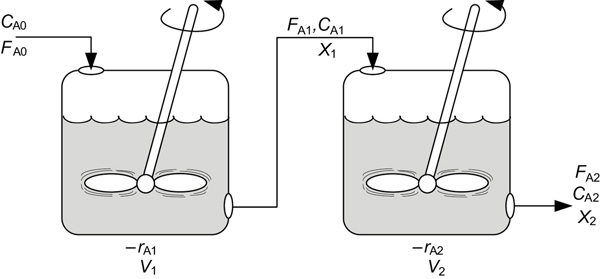
Figure 5-7 Two CSTRs in series.
The effluent concentration of reactant A from the first CSTR can be found using Equation (5-9)
with τ1 = V1/υ0. From a mole balance on reactor 2 one obtains
Solving for CA2, the concentration exiting the second reactor, we obtain
First-order reaction
If both reactors are of equal size (τ1 = τ2 = τ) and operate at the same temperature (k1 = k2 = k), then
If, instead of two CSTRs in series, we had n equal-sized CSTRs connected in series (τ1 = τ2 = … = τn = τi = (Vi/υ0)) operating at the same temperature (k1 = k2 = … = kn = k), the concentration leaving the last reactor would be
Substituting for CAn in terms of conversion
CSTRs in series
and rearranging, the conversion for these identical n tank reactors in series will be
Conversion as a function of the number of tanks in series
Recall from Chapter 2, Figure 2-6, that as the number of tanks n becomes large, the conversion approaches that of a PFR.
A plot of the conversion as a function of the number of CSTRs (i.e., tanks) in series for a first-order reaction is shown in Figure 5-8 for various values of the Damköhler number τk. Observe from Figure 5-8 that when the product of the space time and the specific reaction rate is relatively large, say, Da1 ≥ 1, approximately 90% conversion is achieved in two or three reactors;
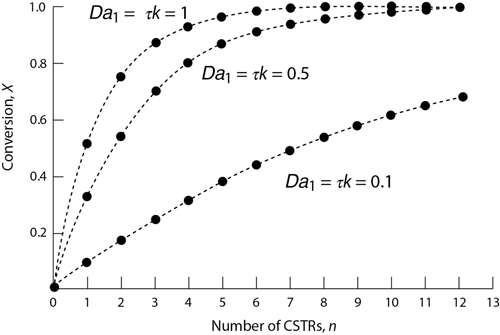
Figure 5-8 Conversion as a function of the number of CSTRs (i.e., tanks) in series for different Damköhler numbers for a first-order reaction.
Economics
thus, the cost of adding subsequent reactors might not be justified. When the product τk is small, Da1 ∽ 0.1, the conversion continues to increase significantly with each reactor added.
The rate of disappearance of A in the nth reactor is
Example 5–2 Producing 200 Million Pounds per Year in a CSTR
Globally, close to 60 billion pounds of ethylene glycol (EG) were produced in 2016. It previously ranked as the 26th most produced chemical in the nation on a total pound basis. About one-half of the ethylene glycol is used for antifreeze, while the other half is used in the manufacture of polyesters. In the polyester category, 88% was used for fibers and 12% for the manufacture of bottles and films. The 2017 selling price for ethylene glycol was $0.43 per pound.
Uses and economics
It is desired to produce 200 million pounds per year of EG. The reactor is to be operated isothermally. A 16.1 mol/dm3 solution of ethylene oxide (EO) in water is mixed (see Figure E5-2.1) with an equal volumetric solution of water containing 0.9 wt % of the catalyst H2SO4 and fed to a CSTR. The pseudo first-order specific reaction-rate constant is 0.311 min–1, as determined in Example 5-1. Practical guidelines for reactor scale-up are given by Mukesh.1
If 80% conversion is to be achieved, determine the necessary CSTR volume.
If two 800-gal reactors were arranged in parallel with the feed equally divided, what would be the corresponding conversion?
If two 800-gal reactors were arranged in series, what would be the corresponding conversion?
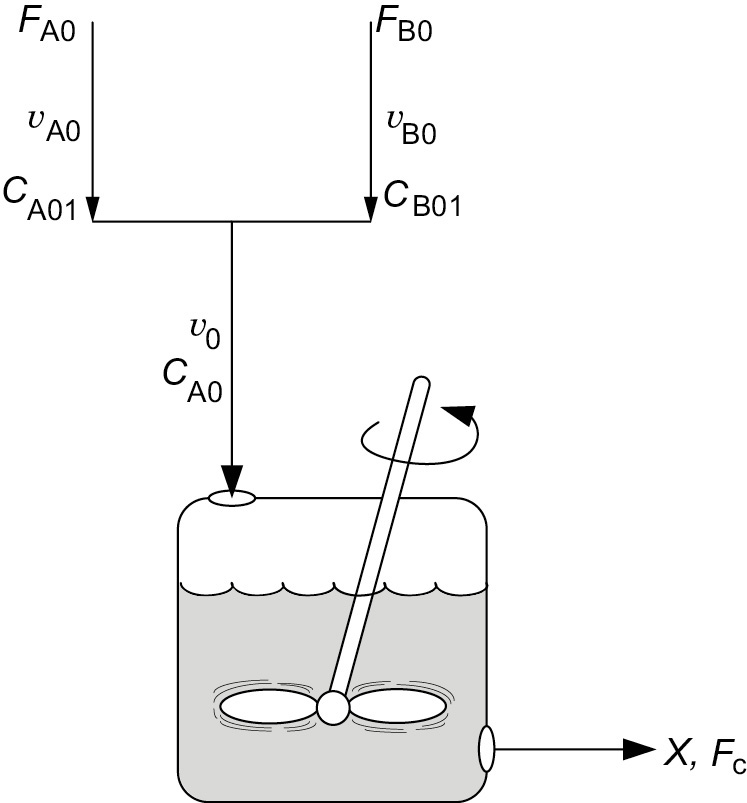
Figure E5-2.1 Single CSTR.
Scale-up of batch reactor data
1 D. Mukesh, Chemical Engineering, 46 (January 2002), www.CHE.com.
Solution
Assumption: Ethylene glycol (EG) is the only reaction product formed.


Ethylene Glycol
First let’s calculate the molar feed rate, FA0, required to produce the ethylene glycol required.
The specified ethylene glycol (EG) production rate in mol/s is
From the reaction stoichiometry
FC = FA0 X
we find the required molar flow rate of ethylene oxide for 80% conversion to be
Answer
We now calculate the single CSTR volume to achieve 80% conversion using the CRE algorithm.
CSTR Mole Balance:
Rate Law:

Stoichiometry: Liquid phase (υ = υ0):
Combining:
Evaluate:
The entering volumetric flow rate of stream A, with CA01 = 16.1 mol/dm3 before mixing, is
From the problem statement υB0 = υA0
The total entering volumetric flow rate of liquid is
Substituting in Equation (E5-2.4), recalling that k = 0.311 min–1, yields
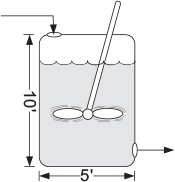
A tank 5 ft in diameter and approximately 10 ft tall is necessary to achieve 80% conversion.
1500-gal tank
CSTRs in parallel. Can you guess what would happen if two 800-gal CSTRs arranged in parallel, as shown in Figure E5-2.2, had a volumetric flow rate υ0 = 3.62 dm3/s fed to each reactor?
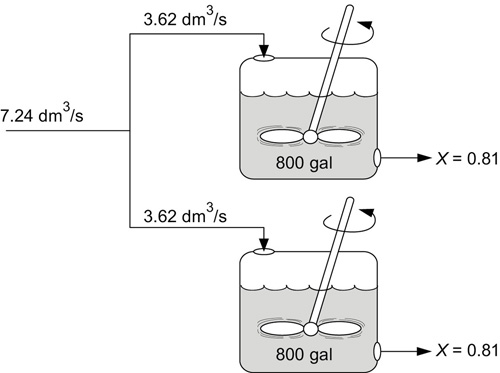
Figure E5-2.2 CSTRs in parallel.
Would the conversion increase, decrease, or remain the same?
To find out, let’s begin by rearranging Equation (E5-2.4)
to obtain
where
The Damköhler number for a first-order reaction is
Da1 = τk = 836.5 s × 0.0052 s–1 = 4.35
Substituting into Equation (E5-2.5) gives us
The conversion exiting both of the CSTRs in parallel is 81%.
Question Q5-6B asks you to generalize the result for n equal-size reactors Vi in parallel with equal feed rates (FA0/n) and show that the conversion would also be the same if everything were fed to one big reactor of volume V = nVi.
CSTRs in series. Recalling what we found in Chapter 2 when we sequenced reactors, can you guess what will happen to the conversion in Part (a) if the reactors are placed in series? Will it increase or decrease? If the 800-gal reactors are arranged in series as shown in Figure E5-2.3, the conversion in the first reactor (cf. Equation (E5-2.5)) is
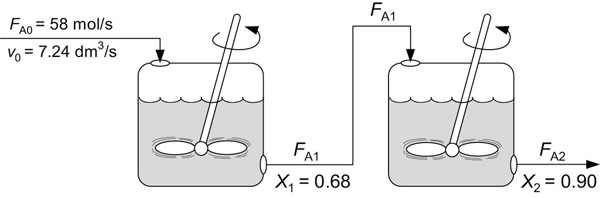
Figure E5-2.3 CSTRs in series.
where
The Damköhler number for the first CSTR is
First CSTR
the corresponding conversion in the first CSTR is
To calculate the conversion exiting the second reactor, we recall that V1 = V2 = V and υ01 = υ02 = υ0; then
τ1 = τ2 = τ
Conversion in the series arrangement is greater than in parallel for CSTRs. From our discussion of reactor staging in Chapter 2, we could have predicted that the series arrangement would have given the higher conversion.
A mole balance on the second reactor is
Basing the conversion on the total number of moles reacted up to a point per mole of A fed to the first reactor
FA1 = FA0 (1 – X1) and FA2 = FA0 (1 – X2)
Second CSTR
Rearranging
Combining the mole balance on the second reactor (cf. Equation (2-24)) with the rate law, we obtain
Solving Equation (E5-2.7) for the conversion exiting the second reactor yields
The same result could have been obtained from Equation (5-15)
Over two hundred million pounds of EG per year can be produced using two 800-gal (3.0-m3) reactors in series.
Analysis: The CRE algorithm was applied to a first-order irreversible liquid-phase reaction carried out isothermally in a single CSTR, two CSTRs in series, and also two CSTRs in parallel. The equations were solved algebraically for each case. When the entering molar flow rate was equally divided between the two CSTRs in parallel, the overall conversion was the same as that for a single CSTR. For two CSTRs in series, the overall conversion was greater than that of a single CSTR. This result will always be the case for isothermal reactions with power-law rate laws with reaction orders greater than zero.
Safety Considerations
We can find information online about the safety of ethylene glycol and other chemicals from Table 5-4. One source is the Vermont Safety Information Resources, Inc., Web site (Vermont SIRI, www.siri.org). For example, we can learn from the Control Measures that we should use neoprene gloves when handling the material, and that we should avoid breathing the vapors. If we click on “Dow Chemical USA” and scroll the Reactivity Data, we would find that ethylene glycol will ignite in air at 413°C.
Safety information MSDS
TABLE 5-4 ACCESSING SAFETY INFORMATION
|
For ethylene oxide go to Cameo Chemicals (https://cameochemicals.noaa.gov/chemical/694).
5.4 Tubular Reactors
Gas-phase reactions are carried out primarily in tubular reactors where the flow is generally turbulent. By assuming that there is no dispersion and there are no radial gradients in either temperature, velocity, concentration, or reaction rate, we can model the flow in the reactor as plug flow.2
2 Laminar flow reactors (LFRs) and dispersion effects are discussed in Chapter 17. As a general rule, the conversion calculated for a PFR will not be significantly different than that for an LFR. For example, from Table E17-1.1 in Chapter 17, we see on page 895 that when τk = 0.1 then XPFR = 0.095 and XLFR = 0.09, when τk = 2.0 then XPFR = 0.865 and XLFR = 0.78 and when τk = 4, then XPFR = 0.98 and XLFR = 0.94.
Figure 1-9 (Revisited) tubular reactor.
(http://encyclopedia.che.engin.umich.edu/Pages/Reactors/PBR/PBR.html)
The differential form of the PFR design equation such as
Use this differential form of the PFR/PBR mole balances when there is ΔP or heat effects.
must be used when there is a pressure drop in the reactor or heat exchange between the PFR and the surroundings.
In the absence of pressure drop or heat exchange, the integral form of the plug-flow design equation can be used,

As an example, consider the elementary reaction
for which the rate law is
Rate Law
We shall first consider the reaction to take place as a liquid-phase reaction and then as a gas-phase reaction. For the gas phase, we will have to specify the products to learn whether there is a change in the total number of moles in order to calculate δ.
5.4.1 Liquid-Phase Reactions in a PFR ∴ υ = υ0
The combined PFR mole balance and rate law is
If the reaction is carried out in the liquid phase, the concentration of A is
CA = CA0 (1 – X)
Stoichiometry (liquid phase)
and for isothermal operation, we can bring k outside the integral
Combine
This equation gives the reactor volume to achieve a conversion X. Dividing by υ0 (τ = V/υ0) and solving for conversion, we find
Evaluate
where Da2 is the Damköhler number for a second-order reaction, that is, tkCA0.
5.4.2 Gas-Phase Reactions in a PFR [υ = υ0 (1 + εX) (T/T0)(P0/P)]
For constant-temperature (T = T0) and constant-pressure (P = P0) gas-phase reactions, the concentration in Table 4-3 is expressed as a function of conversion
Stoichiometry (gas phase)
and then combining the PFR mole balance, rate law, and stoichiometry
Combine
The entering concentration CA0 can be taken outside the integral sign since it is not a function of conversion. Because the reaction is carried out isothermally, the specific reaction-rate constant, k, can also be taken outside the integral sign.
For an isothermal reaction, k is constant.
From the integral equations in Appendix A.1, we find that
Evaluate
Reactor volume for a second-order gas-phase reaction
5.4.3 Effect of ε on Conversion
We now look at the effect of the change in the total number of moles in the gas phase on the relationship between conversion and volume. For constant temperature and pressure, Equation (4-23) becomes
υ = υ0 (1 + εX)
T = T0
P = P0 (∴p = 1)
Let’s now consider three types of reactions, one in which ε = 0 (i.e., δ = 0), one in which ε < 0 (δ < 0), and one in which ε > 0 (δ > 0). When there is no change in the number of moles with reaction (e.g., A → B), δ = 0 and therefore ε = 0, then the fluid moves through the reactor at a constant volumetric flow rate (υ = υ0) as the conversion increases.
When there is a decrease in the number of moles (δ < 0, ε < 0) in the gas phase, the volumetric gas flow rate decreases and the conversion increases. For example, when pure A enters for the reaction 2A → B, and taking A as the basis of calculation, then A → B/2 and we have
υ = υ0(1 – 0.5X)
Consequently, the gas molecules will spend more time in the reactor than they would if the flow rate were constant, υ = υ0. As a result, this longer residence time would result in a higher conversion than if the flow rate, υ, were constant at υ0.
On the other hand, if there is an increase in the total number of moles (δ > 0, ε > 0) in the gas phase, then the volumetric flow rate, υ, will increase as the conversion increases. For example, for the reaction A → 2B, then ε = yA0δ = 1 (2 – 1) = 1
υ = υ0(1 + X)
and the molecules will spend less time in the reactor than they would if the volumetric flow rate were constant. As a result of this smaller residence time in the reactor, the conversion will be less than what would result if the volumetric flow rate, υ, were constant at υ0.
The importance of changes in volumetric flow rate (i.e., ε ≠ 0) with reaction
Figure 5-9 shows the volumetric flow rate profiles for the three cases just discussed. We note that for the numbers chosen here we see that at the end of the reactor, virtually complete conversion has been achieved.
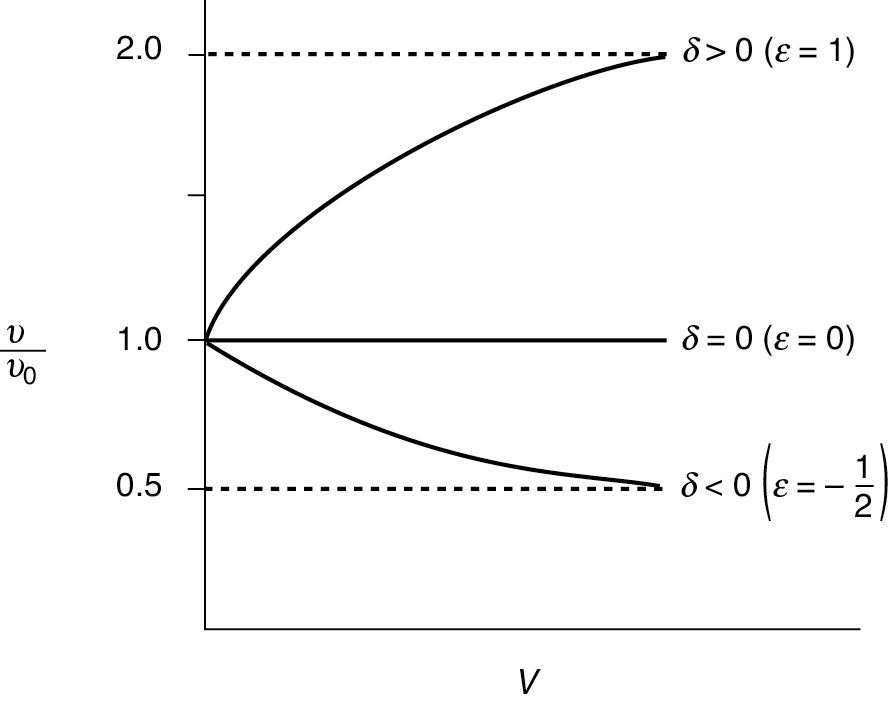
Figure 5-9 Change in gas-phase volumetric flow rate down the length of the reactor.
Example 5–3 Producing 300 Million Pounds per Year of Ethylene in a Plug-Flow Reactor: Design of a Full-Scale Tubular Reactor
Ethylene ranks first in the United States in total pounds of organic chemicals produced each year, and it is the number one organic chemical produced each year. Over 60 billion pounds were produced in 2016, and it sold for $0.28 per pound. Sixty percent of the ethylene produced is used in the manufacture of polyethylene, 15% for ethylene oxide, 10% for ethylene dichloride, 6% for ethyl benzene, and 9% for other products.
The economics
The uses
Determine the plug-flow reactor volume necessary to produce 300 million pounds of ethylene per year by cracking a feed stream of pure ethane. The reaction is irreversible and follows an elementary rate law. We want to achieve 80% conversion of ethane, operating the reactor isothermally at 1100 K and at a pressure of 6 atm. The specific reaction rate at 1000 K is 0.072 s–1 and the activation energy is 82000 cal/mol.
Solution

Ethylene
Let A = C2H6, B = C2H4, and C = H2. In symbols,
Because we want the reader to be familiar with both metric units and English units, we will work a few of the examples using English units. Trust me, a number of companies still use concentrations in lb-mol/ft3. To help you relate English and metric units, the corresponding metric units will be given in parenthesis next to the English units. The only step in the algorithm that is different is the evaluation step.
The molar flow rate of ethylene exiting the reactor is
Next, calculate the molar feed rate of ethane, FA0, to produce 0.34 lb mol/s of ethylene when 80% conversion is achieved,
Answer

Plug-Flow Mole Balance:
Mole Balance
Rearranging and integrating for the case of no pressure drop and isothermal operation yields
Rate Law3:
Rate Law
The activation energy is 82 kcal/mol.
3 Ind. Eng. Chem. Process Des. Dev., 14, 218 (1975); Ind. Eng. Chem., 59(5), 70 (1967).
Stoichiometry: For isothermal operation and negligible pressure drop, the concentration of ethane is calculated as follows:
The gas-phase volumetric flow rate at constant T and P is
Stoichiometry
Combine Equations (E5-3.1)–(E5-3.3) to obtain
Combining the design equation, rate law, and stoichiometry
Evaluate:
Since the reaction is carried out isothermally, we can take k outside the integral sign and use Appendix A.1 to carry out our integration.
Analytical Solution
Parameter Evaluation:
Evaluate
Oops! The rate constant k is given as 0.072 s–1 but that is at 1000 K, and we need to calculate k at reaction conditions, which is 1100 K.
Answer

Substituting FA0, k, CA0, ɛ and into Equation (E5-3.6) yields
For X = 0.8,
Answer
It was decided to use a bank of 2-in. schedule-80 pipes in parallel that are 40 ft in length. For schedule-80 pipe, the cross-sectional area, AC, is 0.0205 ft2. The number of pipes, n, necessary is
To determine the concentration and conversion profiles down the length of the reactor, z, we divide the volume equation (E5-3.8) by the cross-sectional area, AC,
The number of PFRs in parallel

100 pipes in parallel
Equation (E5-3.9) was used along with the volume of one pipe, 0.81 ft3, the cross-sectional area of one pipe AC = 0.0205 ft2, and Equations (E5-3.8) and (E5-3.3) to obtain Figure E5-3.1. Using a bank of 100 pipes will give us the reactor volume necessary to make 300 million pounds per year of ethylene from ethane. The concentration and conversion profiles down any one of the pipes are shown in Figure E5-3.1.
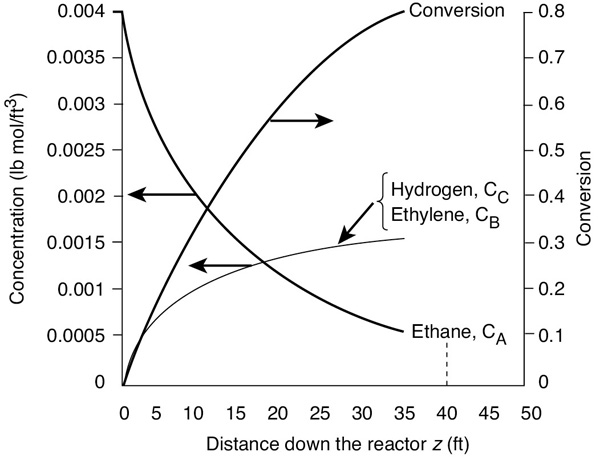
Figure E5-3.1 Conversion and concentration profiles.
Analysis: The CRE algorithm was applied to a gas-phase reaction that had a change in the total number of moles during the reaction. A bank of 100 PFRs in parallel, each with a volume of 0.81 ft3, will give the same conversion as 1 PFR with a volume of 81 ft3. The conversion and concentration profiles are shown in Figure E5-3.1. You will note that the profiles change more rapidly near the entrance to the reactor where the reactant concentrations are high and then change more slowly near the exit where most of the reactants have been consumed, resulting in a smaller rate of reaction.
We will also solve this problem using Polymath, Python, and Wolfram in order to turn it into a Living Example Problem (LEP). To view .cdf files, all you need is Wolfram CDF Player, which can be downloaded for free at http://www.wolfram.com/cdf-player/. We will use the m, kg, s units and the values shown above in parenthesis (e.g., CA0 = 0.066 mol/dm3) in the LEP. The reader should use the “sliders” in Wolfram or Python for this LEP on the CRE Web site (http://www.umich.edu/~elements/6e/05chap/live.html) to vary the parameters and determine their effect on the conversion X.
5.5 Pressure Drop in Reactors
In liquid-phase reactions, the concentration of reactants is insignificantly affected by even relatively large changes in the total pressure. Consequently, we can totally ignore the effect of pressure drop on the rate of reaction when sizing liquid-phase chemical reactors. However, in gas-phase reactions, the concentration of the reacting species is proportional to the total pressure; therefore, proper accounting for the effects of pressure drop on the reaction system can, in many instances, be a key factor in the success or failure of the reactor operation. This fact is especially true in microreactors packed with solid catalyst. Here, the microfluidic channels are so small (see Problem 5-21B) that pressure drop can limit the throughput and conversion for gas-phase reactions.
Pressure drop is ignored for liquid-phase kinetics calculations.
5.5.1 Pressure Drop and the Rate Law
We now focus our attention on accounting for the pressure drop in the rate law. For an ideal gas, we recall Equation (4-25) to write the concentration of reacting species i as
For gas-phase reactions, pressure drop may be very important.
where , ε = yA0δ, and υi is the stoichiometric coefficient (e.g., υA = –1, υB = –b/a). We now must determine the pressure ratio (p = P/P0) as a function of the PFR reactor volume, V, or the PBR catalyst weight, W, to account for pressure drop. We then can combine the concentration, rate law, and PBR mole balance. However, whenever accounting for the effects of pressure drop, the differential form of the mole balance (design equation) must be used.
If, for example, the second-order reaction
is being carried out in a packed-bed reactor, the differential form of the mole balance equation in terms of catalyst weight is
When P ≠ P0, one must use the differential forms of the PFR/PBR design equations.
The rate law is
From stoichiometry for gas-phase reactions (Table 3-5)
and the rate law can be written as
Note from Equation (5-20) that the larger the pressure drop (i.e., the smaller the value of p) from frictional losses, the smaller the reaction rate!
Combining Equation (5-20) with the mole balance (2-17) and assuming isothermal operation (T = T0) gives
Dividing by FA0 (i.e., υ0CA0 yields
For isothermal operation (T = T0), the right-hand side is a function of only conversion and pressure
Another equation is needed (e.g., p = f (W)).
We now need to relate the pressure drop to the catalyst weight in order to determine the conversion as a function of catalyst weight (i.e., catalyst mass).
5.5.2 Flow Through a Packed Bed
The majority of gas-phase reactions are catalyzed by passing the reactant through a packed bed of catalyst particles.

The equation used most often to calculate pressure drop in a packed porous bed is the Ergun equation4,5:
4 R. B. Bird, W. E. Stewart, and E. N. Lightfoot, Transport Phenomena, 2nd ed. New York: Wiley, 2002, p. 191.
5 A slightly different set of constants for the Ergun Equation (e.g., 1.8G instead of 1.75G) can be found in Ind. Eng. Chem. Fundamentals, 18 (1979), p. 199.
Ergun equation
Term 1 is dominant for laminar flow, and Term 2 is dominant for turbulent flow, where
P |
= pressure (lbf/ft2, (bar), or (kPa) |
ϕ |
= |
1 − ϕ |
= |
gc |
= 32.174 lbm · ft/s2 · lbf conversion factor |
= 4.17 × 108 lbm · ft/h2 · lbf |
|
(Recall that for the metric system gc = 1.0) |
|
DP |
= diameter of particle in the bed, ft or (m) |
μ |
= viscosity of gas passing through the bed, (lbm/ft·h) or (kg/m · s) |
z |
= length down the packed bed of pipe, (ft) or (m) |
u |
= superficial velocity = volumetric flow rate ÷ cross-sectional area of pipe, (ft/h) or (m/s) |
ρ |
= gas density, (lbm/ft3) or (kg/m3) |
G |
= ρu = superficial mass velocity, (lbm/ft2 · h) or (kg/m2 · s) |
In calculating the pressure drop using the Ergun equation, the only parameter that varies with pressure on the right-hand side of Equation (5-22) is the gas density, ρ. We are now going to calculate the pressure drop through a packed-bed reactor.
Because the PBR is operated at steady state, the mass flow rate at any point down the reactor, (kg/s), is equal to the entering mass flow rate, (i.e., equation of continuity)
Recalling Equation (4-16), we have
Combining Equations (5-22) and (5-23) gives
Simplifying yields
where β0 is a constant that depends only on the properties of the packed bed (ϕ, DP) and the fluid properties at the entrance conditions (i.e., μ, G, ρ0, T0, P0). Typical units of β0 are (atm/ft), (bar/m), or (kPa/m).
For tubular packed-bed reactors, we are more interested in catalyst weight rather than the distance z down the reactor. The catalyst weight up to a distance of z down the reactor is
where Ac is the cross-sectional area. The bulk density of the catalyst, ρb (mass of catalyst per volume of reactor bed), is just the product of the density of the solid catalyst particles, ρc, and the fraction of solids, (1 – ϕ):
ρb = ρc (1 – ϕ)
Bulk density
Using the relationship between z and W (Equation (5-26)), we can change our variables to express the Ergun equation in terms of catalyst weight:
Use this form for multiple reactions and membrane reactors.
Further simplification yields
Again, let p = (P/P0), then
Used for multiple reactions
where
and where typical units of α might be (kg–1) or .
We will use Equation (5-28) when multiple reactions are occurring or when there is pressure drop in a membrane reactor. However, for single reactions in packed-bed reactors, it is more convenient to express the Ergun equation in terms of the conversion X. Recalling Equation (4-20) for FT,
Differential form of Ergun equation for the pressure drop in packed beds
where, as before
Substituting for the ratio (FT/FT0), Equation (5-28) can now be written as
Use for single reactions
We note that when is negative, the pressure drop ΔP will be less (i.e., higher pressure) than that for ε = 0. When ε is positive, the pressure drop ΔP will be greater (i.e., lower pressure) than when ε = 0.
For isothermal operation, Equation (5-30) is only a function of conversion and pressure
Recalling Equation (5-21), for the combined mole balance, rate law, and stoichiometry
Two coupled equations to be solved numerically
we see that we have two coupled first-order differential equations, (5-31) and (5-21), that must be solved simultaneously. A variety of software packages (e.g., Poly-math) and numerical integration schemes are available for this purpose.
Analytical Solutions. If ε = 0, or if we can neglect (εX) with respect to 1.0 (i.e., εX ≪ 1), we can obtain an analytical solution to Equation (5-30) for iso-thermal operation (i.e., T = T0). For isothermal operation with ε = 0, Equation (5-30) becomes
Isothermal with ε = 0
Rearranging gives
Taking p inside the derivative, we have
Integrating with p = 1 (P = P0) at W = 0 yields
p2 = (1 – αW)
Taking the square root of both sides gives
Pressure ratio only for ε = 0 and isothermal
Be sure not to use this equation if ε ≠ 0 or if the reaction is not carried out isothermally. The pressure-drop parameter α is

Equation (5-33) can be used to substitute for the pressure in the rate law, in which case the mole balance can then be written solely as a function of conversion and catalyst weight. The resulting equation can readily be solved either analytically or numerically.
If we wish to express the pressure in terms of reactor length z, we can use Equation (5-26) to substitute for W in Equation (5-33). Then
from which one can plot the pressure along the length of the reactor.
5.5.3 Pressure Drop in Pipes
Normally, the pressure drop for gases flowing through pipes without packing can be neglected. For flow in pipes, the pressure drop along the length of the pipe can be approximated by
where
and where fF usually is the Fanning friction factor, D is the pipe diameter, and the other parameters are the same as previously defined.
For the flow conditions given in Example (5-4) in a 1000-ft length of 1½-in. schedule-40 pipe (αp = 0.05 m–3), the pressure drop is usually less than 5%. However, for high volumetric flow rates through microreactors, the pressure drop might be significant. See sample calculation on the Web site at http://www.umich.edu/~elements/6e/05chap/pdf/alpha-P-calculation-Example-5-4.pdf.
Example 5–4 Calculating Pressure Drop in a Packed Bed
Plot the pressure drop in a 60-ft length of 1½-in. schedule-40 pipe packed with catalyst pellets ¼ in. in diameter. There is 104.4 lbm/h of gas passing through the bed. The temperature is constant along the length of pipe at 260°C. The void fraction is 45% and the properties of the gas are similar to those of air at this temperature. The entering pressure is 10 atm.
Solution
First let’s calculate the total pressure drop.
At the end of the reactor, z = L, Equation (5-34) becomes
Evaluating the pressure-drop parameters
We now look up the cross-sectional area for 1½-in. schedule-40 pipe, to find Ac = 0.01414 ft2
For air at 260°C and 10 atm we find
Evaluating the parameters in the Ergun equation
From the problem statement
Substituting these values into Equation (5-25) gives

Tedious reading and calculations, but we gotta know how to do the nitty-gritty.
We note that the turbulent flow term, Term 2, is dominant
Unit conversion for
We are now in a position to calculate the total pressure drop ΔP
Now let’s use Equation (E5-4.1) to plot the pressure and Equation (4-16) to plot the volumetric flow rate profiles. Recalling Equation (5-23) for the case ε = 0 and T = T0
Equations (5-34) and (E5-4.8) were used in the construction of Table E5-4.1.
TABLE E5-4.1 P AND υ PROFILES
z (ft) |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
P (atm) |
10 |
9.2 |
8.3 |
7.3 |
6.2 |
4.7 |
2.65 |
υ (ft3/h) |
253 |
275 |
305 |
347 |
408 |
538 |
955 |
For ρc = 120 lbm/ft3
Typical value of α
Equations (E5-4.1) and (E5-4.8), along with the values in Table E5-4.1, were used to obtain Figure E5-4.1.
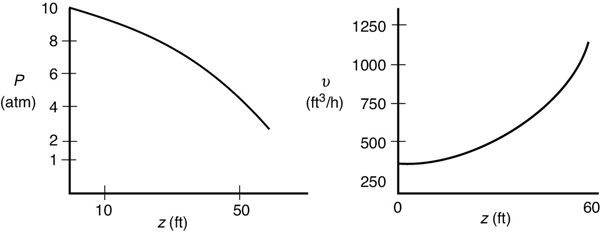
Figure E5-4.1 Pressure and volumetric flow rate profiles (z = W/Acρc (1 - ϕ))).
Note how the volumetric flow rate increases dramatically as we move down the reactor. Visit LEP P5-4 on the CRE Web site and use Wolfram or Python to see how p and f change as one varies the pressure drop parameters in the Ergun Equation. Write three conclusions from your Wolfram or Python experiments.
Analysis: This example showed how to calculate the pressure drop and pressure-drop parameters (α and β0) for a gas flowing through a packed-bed reactor. The pressure and volumetric flow rate profiles were then calculated as a function of z down the packed catalyst bed (i.e., catalyst weight), and shown in Figure E5-4.1. Recall from Equation (5-26) W = [(1–ϕ)Acρc]z. One thing I bet you did not expect in this figure is how much the volumetric flow rate increases as the pressure decreases as one moves down the length of the PBR.
5.5.4 Analytical Solution for Reaction with Pressure Drop
Let’s reason out how pressure drop affects our CRE algorithm. Figure 5-10 shows qualitatively the effects of pressure drop on reactor design. Starting with Figure 5-10(a), we see how the Ergun equation predicts the pressure decreases as the catalyst weight increases down the packed-bed reactor. The subsequent figures, (b)–(e), show this effect of pressure drop on concentration, reaction rate, conversion, and volumetric flow rate, respectively. Each of these figures compares the respective profiles when there is a pressure-drop with those profiles for no pressure drop. We see that when there is pressure drop in the reactor, the reactant concentrations, and thus reaction rate for reaction (for reaction orders greater than 0 order), will always be smaller than the case with no pressure drop. As a result of this smaller reaction rate, the conversion will be less with pressure drop than without pressure drop. Trust me on this next suggestion. Go to the CRE Web site, Chapter 5 YouTube videos (http://www.umich.edu/~elements/6e/youtube/index.html) and click on the funny video Chemical Reaction Engineering Gone Wrong. The students worked very hard on this video and if you don’t like it, I will buy you a Little Mac sandwich at the AIChE Student Chapter meeting in 2021.
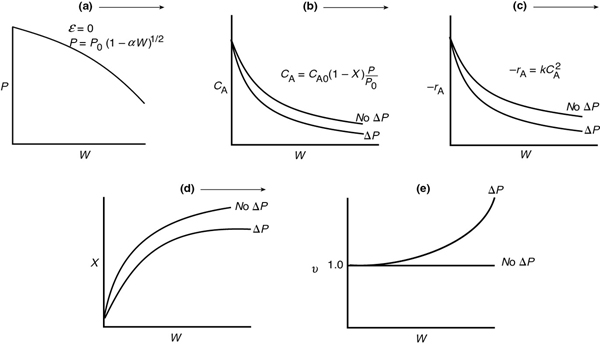
Figure 5-10 Effect of pressure drop on P (a), CA (b), –rA(c), X (d), and υ(e).
How will pressure drop, ΔP, affect our reactor calculations?
Second-Order Gas-Phase Reaction in a PBR with Pressure Drop
Now that we have expressed pressure as a function of catalyst weight (Equation (5-33) for ε = 0), we can return to the second-order isothermal reaction
to relate conversion and catalyst weight. Recall our mole balance, rate law, and stoichiometry.
Mole Balance:
Rate Law:
Stoichiometry: Gas-phase isothermal reaction (T = T0) with ε = 0. From Equation (5-23), υ = υ0/p
Only for ε = 0
Using Equation (5-33) to substitute for p in terms of the catalyst weight, we obtain
CA = CA0 (1 – X) (1 – αW)1/2

Combining:
Separating Variables:
Integrating with limits X = 0 when W = 0 and substituting for FA0 = CA0υ0 yields
We can solve the above equation to either find X at a given W, or find W necessary to achieve a given X.
A Solving for conversion gives
6. B Solving for the catalyst weight, we have
Catalyst weight for second-order reaction in PBR with ΔP
Example 5–5 Effect of Pressure Drop on the Conversion Profile
Reconsider the packed-bed reactor in Example 5-4 for the case where a second-order reaction
2A → B + C
is taking place in 20 m of a 1½-in. schedule-40 pipe packed with catalyst. The flow and packed-bed conditions in Example 5-4 remain the same here except that they are converted to SI units; that is, P0 = 10 atm = 1013 kPa, and
Entering volumetric flow rate: υ0 = 7.15 m3/h (252 ft3/h)
Catalyst pellet size: Dp = 0.006 m (ca. ¼ in.)
Solid catalyst density: ρc = 1923 kg/m3 or (120 lbm/ft3)
Cross-sectional area of 1½-in. schedule-40 pipe: AC = 0.0013 m2
Pressure-drop parameter: β0 = 25.8 kPa/m
Reactor length: L = 20 m
We need to be able to work either metric, SI, or English units.
We will vary the particle size to learn its effect on the conversion profile. However, we will assume that the specific reaction rate, k, is unaffected by particle size, an assumption that we know from Chapters 14 and 15 is valid only for small particles.
First, calculate the conversion in the absence of pressure drop.
Next, calculate the conversion accounting for pressure drop.
Finally, determine how your answer to (b) would change if the catalyst particle diameter were doubled.
The entering concentration of A is 0.1 kmol/m3 and the specific reaction rate is
Solution
We use Equation (5-38) to calculate the conversion as a function of catalyst weight.
First, let’s evaluate the parameters. For the bulk catalyst density
ρb = ρc(1 – ϕ) = (1923)(1 – 0.45) = 1058 kg/m3
The weight of catalyst in the 20 m of 1½-in. schedule-40 pipe is
Next, let’s calculate the conversion for no pressure drop, ΔP = 0 (i.e., α = 0)
Next, calculate the conversion with pressure drop. Recalling Equation (5-29) and substituting the bulk density ρb = (1 – ϕ) ρc = 1058 kg/m3.
In Equation (E5-4.9) in Example 5-4 on page 193, we calculated α to be
then
Watch out for under design!
Analysis: We see the predicted conversion dropped from 82.2% to 69.3% because of pressure drop. It would be not only embarrassing but also an economic disaster if we had neglected pressure drop and the actual conversion had turned out to be significantly smaller. This point is emphasized in the five-star (⋆⋆⋆⋆⋆) YouTube video Chemical Engineering Gone Wrong on the CRE Web site (https://www.youtube.com/watch?v=S9mUAXmNqxs).
The Wolfram sliders that can be used to explore this Living Example Problem (LEP) along with the conversion and pressure ratio profiles are shown in Figures E5-5.1 and E5-5.2.

Figure E5-5.1 Wolfram sliders.
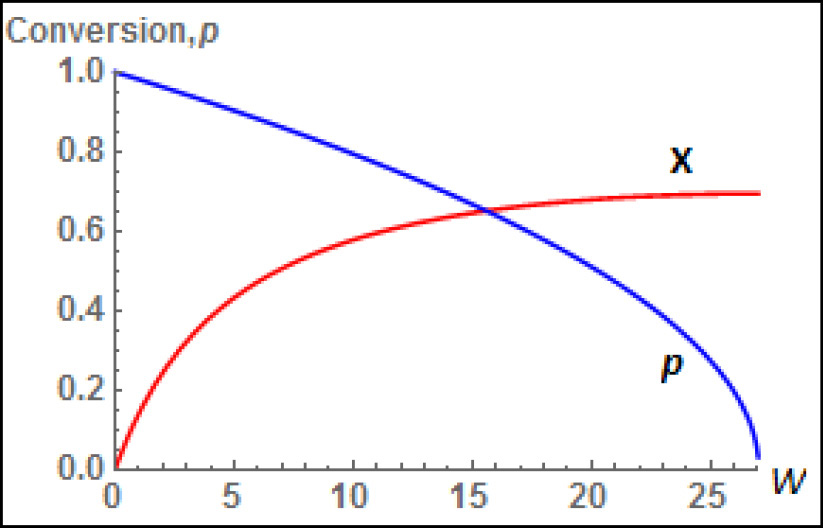
Figure E5-5.2 Wolfram profiles.
After going to the LEP and moving the sliders, be sure to explain why the profiles changed like they did and write three conclusions from your Wolfram or Python experiments.
5.5.5 Robert the Worrier Wonders: What If…
Robert is one of the most important members of our engineering team. He is always trying to anticipate changes and the effect of those changes on the process, not only qualitatively, but quantitatively—a skill all engineers should try to hone. He uses basic engineering analysis to predict the new condition if a change is made or occurs unexpectedly.

Let’s continue Example 5-6 where we now ask a couple of What if… questions. To illustrate engineering analysis, we will address Robert’s worry… What if we decrease the catalyst size by a factor of 4 and increase the entering pressure by a factor of 3? Will the conversion (a) increase, (b) decrease, (c) remain the same, or (d) cannot tell?
Let’s see if we can help Robert out.
First, we need to see how the pressure-drop parameter, α, varies with the system parameters. Combining Equations (5-29) and (5-25), we obtain
Using an average molecular weight of the gas and the ideal gas law, we can express the entering density as
Next, substitute for ρ0 in Equation (5-40) to obtain
We are now going to consider a What if… analysis for laminar and turbulent flow separately. We will only consider changing the superficial mass flow rate, entering pressure, catalyst particle diameter, and cross-sectional area of the tube in which the catalyst is placed. We keep the catalyst pellet density, ρc and void fraction ϕ unchanged and in addition we will leave it as an exercise for the reader to change the temperature and analyze the results.
Laminar Flow Dominant (Term 1 >> Term 2)
We see the pressure-drop parameter α varies as
We now consider the original condition, Case 1, and the condition after a change is made, Case 2, and take the ratio of Case 2 to Case 1.
Case 1 / Case 2
For constant mass flow rate for Case 1 and Case 2, we can substitute for G
to obtain the pressure-drop parameter, α2, for Case 2, after a change in conditions has been made.
α2 for laminar flow
We now proceed for turbulent flow to learn how α varies with the system parameters.
Turbulent Flow Dominant (Term 2 >> Term 1)
We see the pressure-drop parameter varies Taking the ratio of Case 1 to Case 2
Taking the ratio of Case 1 to Case 2
If the mass flow rate, , is the same for the two cases 1 and 2, we can substitute to obtain
α2 for turbulent flow
We observe that for turbulent flow the pressure-drop parameter α is more sensitive to changes to the cross-sectional area AC and less sensitive to changes in the particle diameter DP than that for laminar flow.
Example 5–6 Robert Worries What If…
How will the pressure-drop parameter (e.g., α) and conversion change if you decrease the particle diameter by a factor of 4 and increase entering pressure by a factor of 3, keeping everything else the same? To answer this question we need to consider each flow regime, laminar, and turbulent separately.

His friends sometimes call him “Robert What If.”
For isothermal operation with δ = 0, the relationship between the conversion, X, and the pressure-drop parameter is
Laminar Flow. First, let’s consider how the conversion would change if the flow were laminar.
Here G1 = G2, AC1 = AC2 and T02 = T01, but
Substituting into Equation (5-44)
Substitute α2 into Equation (5-38)
Oops!
The change was not such a good idea as we get much less conversion than before the change. Oops! Robert was indeed right to worry.
Turbulent Flow.
As above, AC1 = AC2 and T02 = T01, but and P02 = 3P01
Solving for our new α and then substituting into Equation (5-38)
Analysis: The following table gives a summary of the conversion for the four cases presented in Example 5-5 for no pressure drop, and the base case and Example 5-6 for laminar and turbulent flow.
1. No pressure drop |
X = 0.82 |
2. Pressure drop (base case) |
X = 0.69 |
3. Pressure drop laminar flow |
X = 0.31 |
4. Pressure drop turbulent flow |
X = 0.78 |
In both laminar and turbulent flow, increasing the pressure, P0, decreases the pressure-drop parameter α. Decreasing the particle diameter Dp increases the pressure-drop parameter α for both laminar and turbulent flow, but more so for the laminar where . The smaller the pressure-drop parameter, α, the smaller the pressure drop and thus the greater will be the conversion. For laminar flow, the negative effects of reducing the particle size by a factor of 4 are stronger than the effect of increasing pressure by a factor of 3.
Robert the Worrier, like the author of this book, thinks it is important to be able to carry out an engineering analysis using Case 1 and Case 2 and then take ratios to estimate the effect of changing parameters on conversion and reactor operation.
Additionally Noted: Because there is no change in the total number of moles during this isothermal gas-phase reaction occurring in a PBR, one can obtain an analytical solution to our CRE algorithm instead of using the Polymath software. Now let’s look at what we could expect by changing the particle diameter of the catalyst pellets.
By increasing the particle diameter, we decrease the pressure-drop parameter and thus increase the reaction rate and the conversion. However, when the catalyst particles become large then interparticle diffusion effects could become important in the catalyst pellet. Consequently, this increase in conversion with increasing particle size to decrease pressure drop will not always be the case (cf. see Figures 10-7, 10-8, Equations (15-54) and (15-57) and Figure 15-4 in Chapter 15). For larger particles, it takes a longer time for a given number of reactant and product molecules to diffuse in and out of the catalyst particle where they undergo reaction (see Figure 10-5). Consequently, the specific reaction rate decreases with increasing particle size, that is, k ~ 1/DP (see Chapter 15, Equation (15-33)), which in turn decreases the conversion.
Let’s summarize these points for large and small particles sizes. At small particle diameters, the rate constant, k, is large and at its maximum value, but the pressure drop is also large, resulting in a low rate of reaction and low conversion. At large particle diameters, the pressure drop is small, but so is the rate constant, k, and the rate of reaction, resulting in low conversion. Thus, we see a low conversion at both large and small particle diameters, consequently there is an optimum in between. This optimum is shown in Figure E5-6.1.
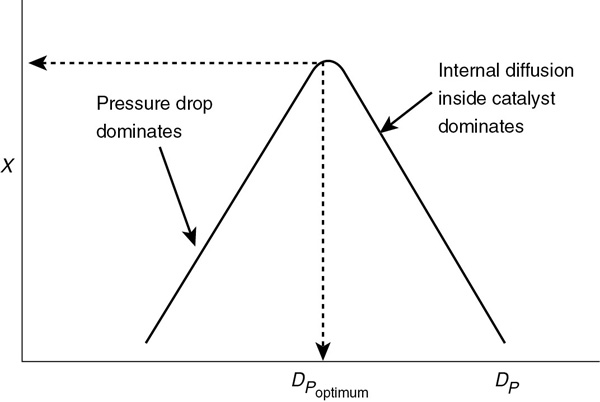
Figure E5-6.1 Finding the optimum particle diameter.
The variation is discussed in detail in Chapter 15. Also, see Chapter 5 Summary Notes.

LEP Sliders
One can now go to the LEP version of Example E5-6 and use the “sliders” in Wolfram to explore the effects of the PBR cross sectional area AC, temperature, T, entering pressure, P0 and the catalyst particle diameter, Dp.
If pressure drop is to be minimized, why not pack the catalyst into a larger diameter tube to decrease the superficial velocity, G, thereby reducing ΔP? There are two reasons for not increasing the tube diameter: (1) There is an increased chance the gas could channel and bypass most of the catalyst, resulting in little conversion; (2) the ratio of the heat-transfer surface area to reactor volume (catalyst weight) will be decreased, thereby making heat transfer more difficult for highly exothermic and endothermic reactions.
Problems with large-diameter tubes
Bypassing of catalyst
Smaller heat-transfer area
We now proceed in Example 5-7 to combine pressure drop with reaction in a packed bed when we have volume change with reaction and therefore cannot obtain an analytical solution.6
6 Ind. Eng. Chem., 45, 234.
Example 5–7 Calculating X in a Reactor with Pressure Drop
Approximately 8.5 billion pounds of ethylene oxide were produced in the United States. The 2014 selling price was $0.86 per pound, amounting to a commercial value of $4.0 billion. Over 60% of the ethylene oxide produced is used to make ethylene glycol. The major end uses of ethylene oxide are antifreeze (30%), polyester (30%), surfactants (10%), and solvents (5%). We want to calculate the catalyst weight necessary to achieve 60% conversion when ethylene oxide is to be made by the vapor-phase catalytic oxidation of ethylene with air.
The economics
The uses
![The chemical equation for the vapor-phase catalytic oxidation of ethylene with air is shown. Ethylene (C2H4) reacts with 0.5 moles of Oxygen (O2) results in the formation of Ethylene oxide [(CH2CH2)O].](http://imgdetail.ebookreading.net/202009/01/9780135486252/9780135486252__elements-of-chemical__9780135486252__graphics__f203_01.jpg)
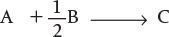
Ethylene and oxygen are fed in stoichiometric proportions to a packed-bed reactor operated isothermally at 260°C. Ethylene is fed at a rate of 136.21 mol/s at a pressure of 10 atm (1013 kPa). It is proposed to use 10 banks of -in. diameter schedule-40 tubes packed with catalyst with 100 tubes per bank. Consequently, the molar flow rate of ethylene to each tube is to be 0.1362 mol/s. The properties of the reacting fluid are to be considered identical to those of air at this temperature and pressure. The density of the 1/4-in. catalyst particles is 1925 kg/m3, the bed void fraction is 0.45, and the gas density is 16 kg/m3. The rate law is
with
The catalyst density, particle size, gas density, void fraction, pipe cross-sectional area, entering pressure, and superficial velocity are the same as in Example E5-4. Consequently we are in luck. Why are we in luck? We don’t have to calculate the pressure-drop parameters β0 and α because they are the same as those calculated in Example 5-4 and we will use these values, that is, β0 = 25.8 atm/m and α = 0.0367 kg–1 in this example.
Solution
Differential Mole Balance:

Rate Law:
Stoichiometry: Gas-phase, isothermal υ = υ0(1 + εX)(P0/P):
The algorithm
For stoichiometric feed
For isothermal operation, Equation (5-30) becomes
We can evaluate the combine step either
Analytically
Graphically
Numerically, or
Using software
Combining the rate law and concentrations
Factoring and recalling PA0 = CA0 RT0, we can simplify Equation (E5-7.7) to
where we have let .
Parameter evaluation per tube (i.e., divide feed rates by 1000)
Evaluating k′, we have
Ethylene:
FA0
=
0.1362 mol/s
Oxygen:
FB0
=
0.068 mol/s
Inerts (N2):
F1
=
Total Entering:
FT0
=
yA0
=
ε
=
PA0
=
yA0P0 = 3.0 atm
As noted in the problem statement, β0 = 25.8 kPa/m and α = 0.0367 kg–1.
Summary: Combining Equations (E5-7.1) through (E5-7.8) and summarizing
To find W given X requires a short trial and error solution.
We will guess the final catalyst weight to achieve 60% conversion to be 27 kg and use this value as the integration end point in our Polymath program.
Wf = 27 kg of catalyst
We have the boundary conditions W = 0, X = 0, p = 1.0, and Wf = 27 kg. Here, we are guessing an upper limit of the integration to be 27 kg, with the expectation that 60% conversion will be achieved within this catalyst weight. If 60% conversion is not achieved, we will guess a higher weight and redo the calculation.
Trial and Error Guess Wf = 27 kg
Living Example Problems (LEPs). As discussed in Section D.2, the LEPs are to be looked at as a piece of equipment on which you can run experiments on the reactor and reactions. With the advent of Wolfram and Python (which can be downloaded for free) this experimentation is a minor paradigm shift in the way we can assign homework problems. One simply moves the slider variable they want to study and observes the change in the reaction profile or trajectory, and then write a set of conclusions. In addition to the simulation experiments, there are a number of other homework problems and we recommend using the Polymath Software to solve these problems. With Polymath, one simply enters Equations (E5-7.9) and (E5-7.10) and the corresponding parameter values (Equations (5-7.11)–(5-7.14)) into the computer with the boundary conditions, and they are solved and the results are displayed as shown in Figures E5-7.1(a) and E5-7.1(b). Equations (E5-7.9) and (E5-7.10) are entered as differential equations and the parameter values are set using explicit equations. The rate law may be entered as an explicit equation with Polymath’s graphing function to generate a plot of the reaction rate as it changes down the length of the reactor. Consequently, one can download the Polymath program directly from the CRE Web site (http://www.umich.edu/~elements/6e/05chap/live.html), which has programmed Equations (E5-7.9)–(E5-7.14), and run the program for different parameter values.

Figure E5-7.1 Output in graphical form from Polymath.
Polymath, MATLAB, Wolfram, and Python program examples can be downloaded from the CRE Web site (see the Introduction).
It is also interesting to learn what happens to the volumetric flow rate as the pressure decreases along the length of the reactor. Recalling Equation (4-23),
We let f be the ratio of the volumetric flow rate, υ, to the entering volumetric flow rate, υ0, at any point down the reactor. For isothermal operation, Equation (4-23) becomes
Volumetric flow rate increases with increasing pressure drop.
The Polymath program and output are shown in Table E5-7.1.
TABLE E5-7.1 POLYMATH PROGRAM AND NUMERICAL OUTPUT
Differential equations
d(X)/d(W) = -raprime/Fao
d(p)/d(W) = -alpha*(1+eps*X)/2/p
Explicit equations
eps = -0.15
kprime = 0.0074
Fao = 0.1362
alpha = 0.0367
raprime = -kprime*(1-X)/(1+eps*X)*p
f = (1+eps*X)/p
rate = -raprime
POLYMATH Report
Ordinary Differential Equations
Calculated values of DEQ variables
|
Variable |
Initial value |
Final value |
1 |
alpha |
0.0367 |
0.0367 |
2 |
eps |
-0.15 |
-0.15 |
3 |
f |
1. |
3.31403 |
4 |
Fao |
0.1362 |
0.1362 |
5 |
kprime |
0.0074 |
0.0074 |
6 |
p |
1. |
0.2716958 |
7 |
raprime |
-0.0074 |
-0.0007504 |
8 |
rate |
0.0074 |
0.0007504 |
9 |
W |
0 |
27. |
10 |
X |
0 |
0.6639461 |
Living Example Problem
For all Living Example Problems, Polymath, Python, Wolfram, can be loaded from the CRE Web site (see the Introduction).
(Information on how to obtain and load the Polymath software can be found in Appendix D. Tutorials can be found on the CRE Web site home page under Living Examples, Polymath.)
A Polymath Video Tutorial (https://www.youtube.com/watch?v=nyJmt6cTiL4)
Figure E5-7.1(a) shows X, p (i.e., p = P/P0), and f (i.e., f = 1/p) down the length of the reactor. We see that both the conversion and the volumetric flow increase along the length of the reactor, while the pressure decreases. Figure E5-7.1(b) shows how the rate of reaction, , decreases as we move down the reactor. For gas-phase reactions with orders greater than zero, the decrease in pressure will cause the reaction rate to be smaller than that in the case of no pressure drop.
From either the conversion profile (shown in Figure E5-7.1) or the Polymath table of results, we find 60% conversion is achieved with 20 kg catalyst in each tube.
We note from Figure E5-7.1 that the catalyst weight necessary to raise the conversion the last 1%, from 65% to 66% (0.9 kg), is 8.5 times more than that required to raise the conversion 1% at the reactor’s entrance. Also, during the last 5% increase in conversion, the pressure decreases from 3.8 to 2.3 atm.
Effect of added catalyst on conversion
This catalyst weight of 20 kg/tube corresponds to a pressure drop of approximately 5 atm. If we had erroneously neglected pressure drop, the catalyst weight would have been found by integrating Equation (E5-7.9) with p = 1 to give
Neglecting pressure drop results in poor design (here, 53% vs. 60% conversion)
But every chemical engineering student in Jofostan knew that!
Analysis: If we had used this 16 kg per tube catalyst weight in our reactor instead of the required 27 kg per tube, we would have had insufficient catalyst to achieve the desired conversion. For this 16 kg catalyst weight, Figure E5-7.1(a) shows that for the case of pressure drop, only 53% conversion would have been achieved and this would have been embarrassing!
Embarrassing!
(To see just how embarrassing, you will need to watch a YouTube video. Go to the CRE Web site, Chapter 5 YouTube videos (http://www.umich.edu/~elements/6e/youtube/index.html) and click on the video Chemical Reaction Engineering Gone Wrong. This note is the second time I have recommended this video because I believe you’ll enjoy it and also get the point.)
In arriving at this job-saving conclusion, we applied the CRE algorithm to a gas-phase reaction with a change in the total number of moles carried out in a PBR. The only small change from the previous example is that we had to use the ODE solver Polymath to combine and solve all the steps to obtain the profiles of the reaction rate (–rA), conversion (X), pressure ratio (p), and volumetric flow rate ratio (f ) as a function of catalyst weight down the length of the PBR.
5.6 Synthesizing the Design of a Chemical Plant
Careful study of the various reactions, reactors, and molar flows of the reactants and products used in the example problems in this chapter reveals that they can be arranged to form a chemical plant to produce 200 million pounds of ethylene glycol from a feedstock of 402 million pounds per year of ethane. The flowsheet for the arrangement of the reactors, together with the molar flow rates, is shown in Figure 5-11. Here, 0.425 lb mol/s of ethane is fed to 100 tubular plug-flow reactors connected in parallel; the total volume is 81 ft3 to produce 0.34 lb mol/s of ethylene (see Example 5-3). The reaction mixture is then fed to a separation unit where 0.04 lb mol/s of ethylene is lost in the separation process in the ethane and hydrogen streams that exit the separator. This process provides a molar flow rate of ethylene of 0.3 lb mol/s, which enters the packed-bed catalytic reactor together with 0.15 lb mol/s of O2 and 0.564 lb mol/s of N2. There are 0.18 lb mol/s of ethylene oxide (see Example 5-6) produced in the 1,000 pipes arranged in parallel and packed with silver-coated catalyst pellets. There is 60% conversion achieved in each pipe and the total catalyst weight in all the pipes is 44,500 lbm. The effluent stream is passed to a separator where 0.03 lb mol/s of ethylene oxide is lost. The ethylene oxide stream is then contacted with water in a gas absorber to produce a 1-lb mol/ft3 solution of ethylene oxide in water. In the absorption process, 0.022 lb mol/s of ethylene oxide is lost. The ethylene oxide solution is fed to a 197-ft3 CSTR, together with a stream of 0.9 wt % H2SO4 solution, to produce ethylene glycol at a rate of 0.102 lb mol/s (see Example 5-2). This rate is equivalent to approximately 200 million pounds of ethylene glycol per year.

Figure 5-11 Production of ethylene glycol.

Synthesizing a chemical plant
Always challenge the assumptions, constraints, and boundaries of the problem.
The profit from a chemical plant will be the difference between income from sales and the cost to produce the chemicals. An approximate formula might be
$$$$
The operating costs include such costs as energy, labor, overhead, and depreciation of equipment. You will learn more about these costs in your senior design course. While most, if not all, of the streams from the separators could be recycled, let’s consider what the profit might be if the streams were to go unrecovered. Also, let’s conservatively estimate the operating and other expenses to be $12 million per year and calculate the profit. Your design instructor might give you a better number. The 2006 prices of ethane, sulfuric acid, and ethylene glycol are $0.17, $0.15, and $0.69 per pound, respectively. See www.chemweek.com for current U.S. prices.
For an ethane feed of 400 million pounds per year and a production rate of 200 million pounds of ethylene glycol per year, the profit is shown in Table 5-5.
TABLE 5-5 PROFITS

You will learn more economics of chemical processing in your senior design class.
Using $58 million per year as a rough estimate of the profit, you can now make different approximations about the conversion, separations, recycle streams, and operating costs to learn how they affect the profit.
5.7 And Now… A Word from Our Sponsor–Safety 5 (AWFOS–S5 A Safety Analysis of the Incident Algorithm)
The Safety Analysis of the Incident is a type of algorithm to analyze an incident to help prevent future accidents. The Chemical Safety Board (CSB) has documented and made videos of a number of accidents that have occurred over the last 40 years. These videos and associated safety modules can be found on the safety website (http://umich.edu/~safeche/). For each safety module you are asked to (1) view the CSB video, (2) fill out the safety analysis algorithm, and (3) perform a few calculations specific to the module, and then fill out the NFPA and Bow Tie Diagrams. After viewing the video, fill out the following Safety Analysis of the Incident. You need to brainstorm all the things that could go wrong and then plan the preventative and mitigating actions.
Safety Analysis of the Incident |
|
Activity: |
------------------------ |
Hazard: |
------------------------ |
Incident: |
------------------------ |
Initiating Event: |
------------------------ |
Preventative Actions and Safeguards: |
------------------------ |
Contingency Plan/Mitigating Actions: |
------------------------ |
Lessons Learned: |
------------------------ |
Definitions
Activity: |
The process, situation, or activity for which risk to people, property, or the environment is being evaluated. |
Hazard: |
A chemical or physical characteristic that has the potential to cause damage to people, property, or the environment. |
Incident: |
What happened? Description of the event or sum of the events along with the steps that lead to one or more undesirable consequences, such as harm to people, damage to the property, to the environment, or asset/business. |
Initiating Event: |
The event that triggers the incident may be at the intersection of two or more failures, (e.g., failure of equipment, instrumentation and controller malfunction, human actions, flammable release). It could also include precursor events that precede the initiating event (e.g., no flow from pump, valve closed, inadvertent human action, ignition). The root cause of the sum events in causing the incident. |
Preventative Actions and Safeguards: |
Steps that can be taken to prevent the initiating event from occurring and becoming an incident that causes damage to people, property, or the environment. Brainstorm all potential problems and hazards that could go wrong. Next, brainstorm and list for each potential problem or hazard all the things that could cause that particular problem to occur (note there may be more than one cause for each potential problem). Finally, for each and every cause, list a preventative action that could be taken to prevent the cause from occurring. |
Contingency Plan/Mitigating Actions: |
Brainstorm and list all the steps that reduce or mitigate the incident after the preventative action fails and the initiating event occurred. |
Lessons Learned: |
What we have learned and can pass on to others that can prevent similar incidents from occurring |
Example
As an example, the Safety Analysis of the Incident will be applied to the accident at Kayak Manufacturing, Material and Energy Balances Safety Module 2 (http://umich.edu/~safeche/assets/pdf/courses/Problems/MaterialsAndEnergy/230Materials&EnergyModule(2)PS072219-WeldingDrum.pdf) on the Process Safety Across the Chemical Engineering Curriculum.
What Happened: In January 2009, a worker at a Kayak Manufacturing Shop in Canada, was welding casters onto an empty acetone drum to make a shop cart. Prior to welding, they rinsed the drum with water and inverted it, but approximately one tablespoon of acetone residue remained in the drum. The worker’s welding arc ignited the acetone and the explosion broke through the bottom of the inverted drum, killing the welder.
Now go ahead and watch the video (https://www.youtube.com/watch?v=9DP5l9yYt-g).
View the video and fill out the Safety Analysis of the Incident.
Solution:
Safety Analysis of the Incident
Activity: The activity in this incident is the hot work on storage drums that once held flammable chemicals. Hot work involves actions that could produce a spark or flame, such as welding, cutting, or grinding.
Hazard: The hazard in this incident is the flammability of acetone residue that was in the drums and its contact with tack welding which acted both as a heat and spark source.
Incident: The incident involved an employee trying to convert an empty acetone drum into a rolling shop cart. The employee rinsed the drum with water from an outdoor hose, agitated the drum, and inverted it to prepare for welding. Even though the drum was rinsed, it was estimated the inverted drum trapped vapor equivalent to approximately one tablespoon of acetone. Grinding the bottom of the drum to prepare for welding helped heat the acetone in the inverted drum. A tack weld perforated the surface and a second tack weld ignited the acetone, creating an explosion that killed a worker. This worker had no formal training in welding.
Initiating Event: The initiating event in this scenario was a spark that resulted from the grinding and welding of a drum that ignited the acetone vapors remaining in the drum.
Preventative Actions and Safeguards: Preventative actions or safeguards could have included safety procedures mandating employees properly dispose of flammable liquid drums and not reuse them, not perform hot work (e.g., grinding or welding) on or near flammable liquid drums (even when empty and rinsed). The manufacturer’s material safety data sheet (MSDS) warnings and procedures for proper use and disposal of drums must be followed along with proper supervision of employees when welding and doing hot work. In addition, there should be proper training for employees who will be welding, education of all employees who use flammable substances on the proper, safe handling of drums and flammables, and having a safely designated welding area.
Contingency Plan/Mitigating Actions: Mitigating actions include training workers in emergency response and first aid procedures, as well as wearing personal protection equipment (PPE) such as fire-resistant clothing and a full face shield or helmet.
Lessons Learned: The lesson learned from this incident is that one tablespoon of a flammable liquid combined with heat and a spark source is sufficient to kill someone. Hot work should not be done on or near flammable liquid containers, even if they have been rinsed with water. Empty flammable liquid containers must be disposed of properly according to manufacturer’s guidelines and not reused.
Further reading on this incident involving acetone:
Acetone values obtained from NIST: https://webbook.nist.gov/cgi/cbook.cgi?Name=acetone&Units=SI
Antoine constants: A = 4.42448, B = 1312.253, C = –32.445
Molar heat of combustion: –1772 kJ/mol
Summary
Solution algorithm
Mole balances (BR, CSTR, PFR, PBR):
Rate law: For example,
Stoichiometry:
Liquid phase: υ = υ0
Gas phase:
For a PBR
Variable density with ε = 0 or ε X << 1 and isothermal operation:
Combining the rate law and stoichiometry for isothermal operation in a PBR
Solution techniques:
Numerical integration—Simpson’s rule
Table of integrals
Software packages
Polymath
MATLAB
An ODE solver (e.g., Polymath) will combine all the equations for you.
ODE Solver Algorithm
When using an ordinary differential equation (ODE) solver such as Polymath, MATLAB, or Wolfram, it is usually easier to leave the mole balances, rate laws, and concentrations as separate equations, rather than combining them into a single equation as we did to obtain an analytical solution. Writing the equations separately leaves it to the computer to combine them and produce a solution. The Polymath formulation for a packed-bed reactor with pressure drop is given in Table 5-8.1 for an elementary reversible reaction carried out isothermally.
Living Example Problem 5-8: Algorithm for reversible gas-phase reaction
A + B ⇄ 3C
in a packed bed with pressure drop.
TABLE LEP 5-8.1 WOLFRAM, PYTHON, AND POLYMATH SIMULATIONS

Figure E5-8.1 Wolfram sliders.
Go to this LEP on the Web site and use the “sliders” in Wolfram to explore this problem. You can download Wolfram for free at http://www.wolfram.com/cdf-player/. Vary the parameters, k, alpha, and so on, to see how the conversion profile changes. A typical Wolfram output is shown in Figure E5-8.2. Describe the variations you see in the conversion and reaction rate profiles. However, most importantly, be able to explain why the variation is occurring and what causes it to occur.

Figure E5-8.2 Wolfram X and p profiles.
CRE Web Site Materials
(http://umich.edu/~elements/6e/05chap/obj.html#/)
Interactive Computer Games (http://umich.edu/~elements/6e/icm/index.html)
Murder Mystery
(http://umich.edu/~elements/6e/icm/murder.html)


Questions, Simulations, and Problems

The subscript to each of the problem numbers indicates the level of difficulty: A, least difficult; D, most difficult.
A = • B = ▪ C = ♦ D = ♦♦
In each of the following questions and problems, rather than just drawing a box around your answer, write a sentence or two describing how you solved the problem, the assumptions you made, the reasonableness of your answer, what you learned, and any other facts that you want to include. To enhance the quality of your sentences, you may wish to refer to W. Strunk and E. B. White, The Elements of Style, 4th ed. New York: Macmillan, 2000, and Joseph M. Williams, Style: Ten Lessons in Clarity & Grace, 6th ed. Glenview, IL: Scott, Foresman, 1999.
Before solving the problems, state or sketch qualitatively the expected results or trends.
Questions
Q5-1A QBR (Question Before Reading). How do the steps in the design of a CSTR differ from those of a CSTR or a PFR with pressure drop?
Q5-2A i>clicker. Go to the Web site (http://www.umich.edu/~elements/6e/05chap/iclicker_ch5_q1.html) and view at least five i>clicker questions. Choose one that could be used as is, or a variation thereof, to be included on the next exam. You also could consider the opposite case: explain why the question should not be on the next exam. In either case, explain your reasoning.
Q5-3A Read through all the problems at the end of this chapter. Make up and solve an original problem based on the material in this chapter. (a) Use real data and reactions from the literature. (b) Make up a reaction and data. (c) Use an example from everyday life (e.g., making toast or cooking spaghetti). In preparing your original problem, first list the principles you want to get across and why the problem is important. Ask yourself how your example will be different from those in the text or lecture. Other things for you to consider when choosing a problem are relevance, interest, impact of the solution, time required to obtain a solution, and degree of difficulty. Look through some of the journals for data, or to get some ideas for industrially important reactions, or for novel applications of reaction engineering principles (the environment, food processing, etc.). At the end of the problem and solution, describe the creative process used to generate the idea for the problem. (d) Write a question based on the material in this chapter that requires critical thinking. Explain why your question requires critical thinking. Hint: See Table P-2 discussed in the Complete Preface-Introduction on the Web site (http://www.umich.edu/~elements/6e/toc/Preface-Complete.pdf) and apply it to this problem. (e) Listen to the audios on the CRE Web site (www.umich.edu/~elements/6e/index.html) ![]() Lecture Notes, pick one, and describe how you might explain it differently.
Lecture Notes, pick one, and describe how you might explain it differently.
Q5-4A If it takes 11 minutes to cook spaghetti in Ann Arbor, Michigan, and 14 minutes in Boulder, Colorado, how long would it take in Cuzco, Peru? Discuss ways to make the spaghetti more tasty. If you prefer to make a creative spaghetti dinner for family or friends rather than answering this question, that’s OK, too; you’ll get full credit—but only if you turn in your recipe and bring your instructor a taste.
Q5-5A Example 5-1. (1) What would be the error in k if the batch reactor were only 80% filled with the same concentrations of reactants, instead of being completely filled as in the example? (2) What generalizations can you draw from this example?
Q5-6B Example 5-2. (1) What conversion would be achieved if three 800-gal CSTRs were placed in series? (2) In parallel with the feed equally divided? (3) What are the advantages and disadvantages of adding this third reactor? (4) FA0 = FA0/n, that conversion achieved in any one of the reactors will be identical to what would be achieved if the reactor were fed in one stream, FA0 = nFAi0, to one large reactor of volume V = nVi.
Q5-7A Example 5-2. Describe how would your reactor volume and number of reactors change if you only needed 50% conversion to produce the 200 million pounds per year required?
Q5-8A Example 5-6. How would the pressure drop and pressure-drop parameters, α and β0, change if the particle diameter were reduced by 25%?
Q5-9A High Finance. (1) How would your profit/numbers change in Table 5-4 if you used the following 2010 prices? (2) Ethylene glycol $0.54/kg, ethylene $0.76/kg, ethylene oxide $1.17/kg, ethane $0.31/kg, sulfuric acid $0.10/kg (98 wgt %), and propylene glycol $1.70/kg. (3) What pops out at you?
Q5-10A Can You Learn a New Dance? View the YouTube video titled CSTR to the tune of “It’s fun to stay at the YMCA” (https://www.youtube.com/watch?v=AkM67QsTq3E) made by the chemical reaction engineering students at the University of Alabama. You can also access it from the CRE Web site (http://www.umich.edu/~elements/6e/index.html); under “Additional Resources,” click on “Fun YouTube Videos.”
Q5-11A Are there steps in the Safety Analysis of the Incident that should be removed or added? If so, what are they?
Q5-12A Go to the five LearnChemE screencasts link for Chapter 5 (http://www.umich.edu/~elements/6e/05chap/learn-cheme-videos.html).
In the screencast of the PBR with pressure drop, is there a problem substituting for the volumetric flow rate when there is a change in the total number of moles, that is, δ ≠ 0?
View one of the other screencasts 5- to 6-minute video tutorials and list two of the most important points.
In the isothermal plug reactor screencast, how does the inert impact the reaction process?
Q5-13A AWFOS–S5 View the CSB video (https://www.youtube.com/watch?v=-_ZLQkn7X-k) and then research the conclusion as to whether or not the safety analysis of the incident is complete.
Computer Simulations and Experiments
P5-1B What if... you were asked to explore the example problems in this chapter to learn the effects of varying the different parameters? This sensitivity analysis can be carried out by downloading the examples from the CRE Web site (www.umich.edu/~elements/6e/index.html, under Living Example Problems (LEPs)). You can download Wolfram for free at http://www.wolfram.com/cdf-player/. For each of the example problems you investigate, write a paragraph describing your findings.
It is important to the learning process that you try to predict how the results change the answer or the shape of the conversion profile before moving a slider.
Example 5-3: Plug Flow Reactor
Wolfram and Python
Write down a conclusion about your variation of each slider and explain why the slider movement gave you the results it did.
What generalizations can you draw from this example?
Example 5-4: Pressure Drop in a Packed Bed
Wolfram and Python
Vary each of the parameters in the Ergun Equation and write a couple of sentences on the variable that changes the slope of p versus z the most, that is, what change increases the pressure drop the most?
What generalizations can you draw from this example?
Example 5-5: Effect of Pressure Drop on Conversion
Wolfram and Python
After varying each slider, write down a conclusion about the conversion and pressure profiles and explain why the slider movement gave you the results it did.
Why do CA, CB, and CC all start to decrease at W = 25 kg?
What generalizations can you draw from this example?
Example 5-6: Robert Worries What If…
Wolfram and Python
Write down a conclusion about your variation of each slider and explain why the slider movement gave you the results it did.
How much would the catalyst weight change if the pressure were increased by a factor of 5 and the particle size decreased by a factor of 5? (Recall that α is also a function of P0.)
Use plots and figures to describe what you learned from this example and how it would apply to other situations.
Example 5-7: Calculating X in a Reactor with Pressure Drop
Wolfram and Python
This problem is a Stop and Smell the Roses Simulation. Explore this simulation to understand the interaction of pressure drop and conversion.

Explain what happens to X, p, and f as k′ moves between its maximum and minimum values from its initial setting of k′ = 0.0035 s–1.
What happens to X, p, and f as alpha moves between its maximum and minimum?
Write two conclusions from your slider experiments.
After reviewing Generating Ideas and Solutions on the Web site (http://www.umich.edu/~elements/6e/toc/SCPS,3rdEdBook(Ch07).pdf), choose one of the brainstorming techniques (e.g., lateral thinking) to suggest two questions that should be included in this problem.
Example 5-8: LEP. Algorithm for A + B = 3C.
Wolfram and Python
Vary k′, CA0, and KC sliders individually between their maximum and minimum values. Write a set of conclusions and explain why the movement of the sliders changed the conversion and pressure drop profiles the way they did.
AspenTech Example 5-3. (1) Using FA0 = 0.425 lbm mol/s, run the AspenTech simulation at 1000 K and at 1200 K and compare with the specified temperature of 1100 K. (2) Explore what a small change in activation energy can make in your results by changing E from 82 to 74 kcal/mol and then to 90 kcal/mol and compare your results with the base case of 82 kcal/mol.
Download Reactor Lab (www.reactorlab.net) onto your computer and call up D1 Isothermal Reactors. Detailed instructions with screen shots are given in Chapter 4 Summary Notes. (1) For L1 Nth Order Reactions, vary the parameters n, E, T for a batch, CSTR, and PFR. Write a paragraph discussing the trends (e.g., first order vs. second order) and describe what you find. (2) Next, choose the “Quiz” at the top of the screen, find the reaction order, (3) and turn in your performance number. Performance number: __________________
Work the Chapter 5 Self-Tests in Summary Notes on the Web. Write a question for this problem that involves critical thinking and explain why it involves critical thinking.
Interactive Computer Games
P5-2B ICG—Mystery Theater—A real “who done it?,” see Pulp and Paper, 25 (January 1993) and also Pulp and Paper, 9 (July 1993). The outcome of the murder trial is summarized in the December 1995 issue of Papermaker, page 12. You will use fundamental chemical engineering from Sections 5.1 to 5.3 to identify the victim and the murderer. #Really? Play the game and then record your performance number.
Performance number: __________________

Who done it?
Problems
P5-3A OEQ (Old Exam Question). Multiple Choice. In each case, you will need to explain the reason you chose the answer you did.
An irreversible, liquid-phase, second-order reaction, A → Product(s), proceeds to 50% conversion in a PFR operating isothermally, isobarically, and at steady state. What conversion would be obtained if the PFR operated at half the original pressure (with all else unchanged)?
(1) >50% (2) <50% (3) 50% (4) Insufficient information to answer definitively
An irreversible, gas-phase, second-order reaction, A → Product(s), proceeds to 50% conversion in a PFR operating isothermally, isobarically, and at steady state. What conversion would be obtained if the PFR operated at half the original pressure (with all else unchanged)?
(1) >50% (2) <50% (3) 50% (4) insufficient information to answer definitively
The rate constant for an irreversible, heterogeneously catalyzed, gas-phase, second-order reaction, A → Product(s), was determined to be 0.234 from experimental data in a packed-bed reactor. The person analyzing the experimental data failed to include the large pressure drop in the reactor in his analysis. If the pressure drop were properly accounted for, the rate constant would be
(1) >0.234 (2) <0.234 (3) 0.234 (4) insufficient information to answer definitively
P5-4B OEQ (Old Exam Question). Multiple Choice. In each of the cases below, (a) through (e), you will need to explain why you chose the answer you did.
The elementary isomerization exothermic reaction
is carried out isothermally at 400 K in a PBR in which pressure drop plays a role, with α = 0.001 kg–1. Currently, 50% conversion is achieved. The equilibrium constant at this temperature is 3.0.
For a fixed mass flow rate , if the reactor diameter is increased by a factor of 4, the conversion will
(1) X > 0.5 (2) X < 0.5 (3) X = 0.5 (4) insufficient information to tell
For a fixed mass flow rate , the equilibrium conversion is
(1) Xe = 0.5 (2) Xe = 0.667 (3) Xe = 0.75 (4) insufficient information to tell
For a fixed mass flow rate , if the reactor diameter is increased by a factor of 2, the equilibrium conversion Xe will
(1) increase (2) decrease (3) remain the same (4) insufficient information to tell
For a fixed mass flow rate , if the particle size is increased, the equilibrium conversion will
(1) increase (2) decrease (3) remain the same (4) insufficient information to tell
For a fixed mass flow rate , if the particle size is increased, the conversion will
(1) increase (2) decrease (3) remain the same (4) insufficient information to tell
Question sets similar to Problems P5-3A and P5-4B that may help you prepare for exams can be found in i>clickers on the Chapter 5 Web site (http://www.umich.edu/~elements/6e/05chap/obj.html).
P5-5A The elementary gas-phase reaction
2A → B
is carried out in a constant-volume batch reactor where 50% conversion is achieved in 1 hour. Pure A is charged to the reactor at an initial concentration of 0.2 mol/dm3. If the same reaction is carried out in a CSTR, what volume would be necessary to achieve 50% conversion for a feed molar flow rate of 500 mol/h and an entering concentration of A of 0.2 mol/dm3? (Ans: V = 5000 dm3)
P5-6C A reversible liquid-phase isomerization A ⇄ B is carried out isothermally in a 1000-gal CSTR. The reaction is second order in both the forward and reverse directions. The liquid enters at the top of the reactor and exits at the bottom. Experimental data taken in a batch reactor shows the CSTR conversion to be 40%. The reaction is reversible with KC = 3.0 at 300 K, and . Assuming that the batch data taken at 300 K are accurate and that E = 15000 cal/mol, what CSTR temperature do you recommend to obtain maximum conversion? Hint: Read Appendix C and assume ΔCP = 0 in the Appendix Equation (C-9):
Use Polymath to make a plot of X versus T. Does it go through a maximum? If so, explain why.
P5-7B OEQ (Old Exam Question). The irreversible gas-phase reaction
A → B + C
follows an elementary rate law and is to be carried out first in a PFR and then in a separate experiment in a CSTR. When pure A is fed to a 10 dm3 PFR at 300 K and a volumetric flow rate of 5 dm3/s, the conversion is 80%. When a mixture of 50% A and 50% inert (I) is fed to a 10 dm3 CSTR at 320 K and a volumetric flow rate of 5 dm3/s, the conversion is also 80%. What is the activation energy in cal/mol?
P5-8B OEQ (Old Exam Question). The elementary gas-phase reaction
A → B
takes place isobarically and isothermally in a PFR where 63.2% conversion is achieved. The feed is pure A. It is proposed to put a CSTR of equal volume upstream of the PFR. Based on the entering molar flow rate of A to the first reactor, what will be the intermediate conversion from the CSTR, X1, and exit conversion from the PFR, X2, based on the feed to first reactor? The entering flow rates and all other variables remain the same as that for the single PFR. Source: Modified California Registration Exam Problem. (Ans: X2 = 0.82)

P5-9A OEQ (Old Exam Question). The liquid-phase reaction
A + B → C
follows an elementary rate law and is carried out isothermally in a flow system. The concentrations of the A and B feed streams are each 2 M before mixing. The volumetric flow rate of each stream is 5 dm3/min, and the entering temperature is 300 K. The streams are mixed immediately before entering. Two reactors are available. One is a gray, 200.0-dm3 CSTR that can be heated to 77°C or cooled to 0°C, and the other is a white, 800.0-dm3 PFR operated at 300 K that cannot be heated or cooled but can be painted red or black. Note that k = 0.07 dm3/mol · min at 300 K and E = 20 kcal/mol.
Which reactor and what conditions do you recommend? Explain the reason for your choice (e.g., color, cost, space available, weather conditions). Back up your reasoning with the appropriate calculations.
How long would it take to achieve 90% conversion in a 200-dm3 batch reactor with CA0 = CB0 = 1 M after mixing at a temperature of 77°C?
What would your answer to part (b) be if the reactor were cooled to 0°C? (Ans: 2.5 days)
What conversion would be obtained if the CSTR and PFR were operated at 300 K and connected in series? In parallel with 5 mol/min to each?
Keeping Table 4-3 in mind, what batch reactor volume would be necessary to process the same amount of species A per day as the flow reactors, while achieving 90% conversion? Referring to Table 1-1, estimate the cost of the batch reactor.
Write a couple of sentences describing what you learned from the problem and what you believe to be the point of the problem.
Apply one or more of the six ideas in Preface Table P-4, page xxvii, to this problem.
P5-10B OEQ (Old Exam Question). Troubleshooting
A liquid-phase isomerization A → B is carried out in a 1000-gal CSTR that has a single impeller located halfway down the reactor. The liquid enters at the top of the reactor and exits at the bottom. The reaction is second order. Experimental data taken in a batch reactor predicted the CSTR conversion should be 50%. However, the conversion measured in the actual CSTR was 57%. Suggest reasons for the discrepancy and suggest something, for example, a model, that would give closer agreement between the predicted and measured conversions. Back your suggestions with calculations. P.S. It was raining very hard that day.
The liquid-phase reaction
was carried out in a CSTR. For an entering concentration of 2 mol/dm3, the conversion was 40%. For the same reactor volume and entering conditions as the CSTR, the expected PFR conversion is 48.6%. However, the PFR conversion was, amazingly, 52.6% exactly. Brainstorm reasons for the disparity. Quantitatively show how these conversions came about (i.e., the expected conversion and the actual conversion). Part (b) is C-level difficulty. #Really?
The gas-phase reaction
is carried out in a packed-bed reactor. When the particle size was decreased by 15%, the conversion remained unchanged. When the particle size was decreased by 20%, the conversion decreased. When the original particle size was increased by 15%, the conversion also decreased. In all cases, the temperature, the total catalyst weight, and all other conditions remained unchanged. What’s going on here?
P5-11B OEQ (Old Exam Question). The irreversible elementary gas-phase reaction
is carried out isothermally at 305 K in a packed-bed reactor with 100 kg of catalyst.

The entering pressure was 20 atm and the exit pressure is 2 atm. The feed is equal molar in A and B and the flow is in the turbulent flow regime, with FA0 = 10 mol/min and CA0 = 0.4 mol/dm3. Currently 80% conversion is achieved. What would be the conversion if the catalyst particle size were doubled and everything else remained the same? (Ans: X = 0.83)
P5-12B The reversible gas-phase elementary reaction

is carried out in an isothermal CSTR with no pressure drop. The feed enters at a volumetric flow rate of . The feed consists of half ethyl benzene (i.e., A) and half inerts on a molar basis and is well mixed before it enters the reactor (I). The pressure in the reactor is 6 atm (so PA0 = 3 atm and PI0 = 3 atm, making the entering concentration of ethyl benzene, A, ). The molar flow rate of A is . At the reaction temperature of 640°C, the rate constant, kA, is . The equilibrium constant, KP, is 9 atm and the corresponding equilibrium conversion is Xe = 0.84.
Reference: Won Jae Lee and Gilbert F. Froment. Ind. Eng. Chem. Res., 47, 9183–9194 (2008).
Write out each step of the algorithm.
Write the rate of reaction, –rA, solely as a function of PA0 X, KP, and k.
Calculate the reactor volume necessary to achieve 90% of the equilibrium conversion, Xe.
How would the conversion from part (a) be affected if the reactor diameter increased and height decreased but total volume remained the same? Explain.
P5-13B While on his way home from a concert by Ann Arbor’s own Bob Seger at Pine Knob, during his visit to Michigan, world famous Inspector Sgt. Nigel Amber-cromby was called in from Scotland Yard when the body of Ian Shoemaker, an English businessman, was discovered outside his home at 6 A.M. the morning of April 1st. Mr. Shoemaker was in the process of investigating why there was money missing from the chemical engineers’ pension fund on March 31st. He met individually over coffee with each of the four employees who had access to the fund on March 31st, to confirm his suspicions before he pressed charges. However, the guilty one must have discovered Shoemaker’s suspicions beforehand and wanted to keep their identity secret by murdering him.

During the autopsy the coroner determined Mr. Shoemaker was poisoned by a chemical known as Iocane powder. Iocane stops the heart from beating and is virtually undetectable, but it decomposes in the blood to form the detectable compound Optoid, according to the reaction
Iocane + RBC → Optoid
Because of the high concentration of red blood cells, CRBC, the rate law between Iocane and the red blood cells can be modeled as a pseudo first-order reaction in terms of the concentration of Iocane, CA,
The coroner told Inspector Ambercromby that during the autopsy at 11 A.M. on April 1st, he found that the concentration of Optoid was 0.01 mol/dm3.
According to his calendar, Shoemaker had meetings the previous day, March 31st, at the following times:
1:30 P.M. (21.5 hours prior) with Mr. Gafhari
3:00 P.M. (20 hours prior) with Mr. Ross
5:00 P.M. (18 hours prior) with Ms. Patel
8:00 P.M. (15 hours prior) with Mr. Jenkins
These four individuals are now the prime suspects. Iocane is available over the counter as a rat poison in powder capsules, each containing 18 g (56.25 g/mol), and a capsule could have easily been put in Shoemaker’s coffee.
Additional information:
Volume of blood: 5 dm3
kA = 0.00944 hr–1 at 310 K (body temperature)
E = 20.5 kcal/mol
Assume the poison goes virtually immediately into the blood.
Calculate the initial concentration CA0 of Iocane in the blood in gmol/dm3 after ingesting one capsule.
Knowing CA0 and the concentration of Optoid at 11 A.M., calculate the time Shoemaker was poisoned. Whom should Ambercromby arrest?
After calculating the time the poison was put in the coffee and arresting the alleged killer, Shoe-maker’s wife mentioned that Shoemaker was running a fever of 311.7 K (101.4 F) that morning. Knowing Shoemaker had a fever, do you think Nigel arrested the right suspect? If not, whom should he arrest?
(Eric O’Neill, U of M, class of 2018)
P5-14B The dehydration of butanol is carried out over a silica-alumina catalyst at 680 K.
The rate law is
with k = 0.054 mol/gcat•h•atm and KBu = 0.32 atm–1. Pure butanol enters a thin-tubed, packed-bed reactor at a molar flow rate of 50 kmol/hr and a pressure of 10 atm (1013•kPa).
What PBR catalyst weight is necessary to achieve 80% conversion in the absence of pressure drop? Plot and analyze X, p, f (i.e., (υ/υ0)) and reaction rate, , as a function of catalyst weight.
What “fluidized CSTR” catalyst weight is necessary to achieve 80% conversion?
Repeat (a) when there is pressure drop, with the pressure-drop parameter α = 0.0006 kg–1. Do you observe a maximum in the rate of reaction, and if so, why? What catalyst weight is necessary to achieve 70% conversion? Compare this weight with that for no pressure drop to achieve the same conversion.
What generalizations can you make about this problem?
Write a question for this problem that requires critical thinking and then explain why your question requires critical thinking. Hint: See Preface Section G.2
P5-15B OEQ (Old Exam Question). The gaseous reaction A → B has a unimolecular reaction rate constant of 0.0015 min–1 at 80°F. This reaction is to be carried out in parallel tubes 10 ft long and 1 in. inside diameter, under a pressure of 132 psig at 260°F. A production rate of 1000 lb/h of B is required. Assuming an activation energy of 25000 cal/mol, how many tubes are needed if the conversion of A is to be 90%? Assume perfect gas laws. A and B each have molecular weights of 58. Source: From California Professional Engineers’ Exam.
P5-16B OEQ (Old Exam Question).
The irreversible elementary reaction 2A → B takes place in the gas phase in an isothermal tubular (plug-flow) reactor. Reactant A and a diluent C are fed in equimolar ratio, and conversion of A is 80%. If the molar feed rate of A is cut in half, what is the conversion of A assuming that the feed rate of C is left unchanged? Assume ideal behavior and that the reactor temperature remains unchanged. What was the point of this problem? Source: From California Professional Engineers’ Exam.
Write a question that requires critical thinking, and explain why it involves critical thinking. (See Preface Section G.2.)
P5-17B OEQ (Old Exam Question). Compound A undergoes a reversible isomerization reaction, A ⇄ B, over a supported metal catalyst. Under pertinent conditions, A and B are liquid, miscible, and of nearly identical density; the equilibrium constant for the reaction (in concentration units) is 5.8. In a fixed-bed iso-thermal flow reactor in which backmixing is negligible (i.e., plug flow), a feed of pure A undergoes a net conversion to B of 55%. The reaction is elementary. If a second, identical flow reactor at the same temperature is placed downstream from the first, what overall conversion of A would you expect if:
The reactors are directly connected in series? (Ans: X = 0.74)
The products from the first reactor are separated by appropriate processing and only the unconverted A is fed to the second reactor?
Apply to this problem one or more of the six ideas discussed in Table P-4 in the Complete Preface-Introduction on the Web Site (http://www.umich.edu/~elements/6e/toc/Preface-Complete.pdf).
P5-18B OEQ (Old Exam Question). A total of 2500 gal/h of metaxylene is being isomerized to a mixture of orthoxylene, metaxylene, and paraxylene in a reactor containing 1000 ft3 of catalyst. The reaction is being carried out at 750°F and 300 psig. Under these conditions, 37% of the metaxylene fed to the reactor is isomerized. At a flow rate of 1667 gal/h, 50% of the metaxylene is isomerized at the same temperature and pressure. Energy changes are negligible.
It is now proposed that a second plant be built to process 5500 gal/h of metaxylene at the same temperature and pressure as described earlier. What size reactor (i.e., what volume of catalyst) is required if conversion in the new plant is to be 46% instead of 37%? Justify any assumptions made for the scale-up calculation. (Ans: 2931 ft3 of catalyst) Make a list of the things you learned from this problem. Source: From California Professional Engineers’ Exam.
P5-19B OEQ (Old Exam Question). It is desired to carry out the gaseous reaction A → B in an existing tubular reactor consisting of 50 parallel tubes 40 ft long with a 0.75-in. inside diameter. Bench-scale experiments have given the reaction rate constant for this first-order reaction as 0.00152 s–1 at 200°F and 0.0740 s–1 at 300°F. At what temperature should the reactor be operated to give a conversion of A of 80% with a feed rate of 500 lb m/h of pure A and an operating pressure of 100 psig? A has a molecular weight of 73 Daltons. Departures from perfect gas behavior may be neglected, and the reverse reaction is insignificant at these conditions. (Ans: T = 278°F) Source: From California Professional Engineers’ Exam.

P5-20B The irreversible first-order (wrt partial pressure of A) gas-phase reaction
A → B
is carried out isothermally in a “fluidized” catalytic CSTR containing 50 kg of catalyst.
Currently, 50% conversion is realized for pure A entering at a pressure of 20 atm. There is virtually no pressure drop in the CSTR. It is proposed to put a PBR containing the same catalyst weight in series with the CSTR. The pressure drop parameter for the PBR, α, given by Equation (5-29) is α = 0.018 kg–1. The particle size is 0.2 mm, the bed porosity is 40%, and the viscosity is the same as that of air at 200°C.
Fluidized CSTR
Should the PBR be placed upstream or downstream of the CSTR in order to achieve the highest conversion? Explain qualitatively using concepts you learned in Chapter 2.
What is the conversion coming out of the first reactor?
What is the conversion exiting the last reactor? (Ans: X = 0.76)
What is the pressure at the exit of the packed bed? (Ans: P = 6.32 atm)
How would your answers change if the catalyst diameter were decreased by a factor of 2 and the PBR diameter were increased by 50%, assuming turbulent flow?
P5-21B A microreactor from the MIT group similar to the one shown in Figure P5-21B was used to produce phosgene in the gas phase. We continue our discussion on microreactors in Chapter 6.

Figure P5-21B Microreactor. (Image courtesy of Ryan Hartman, NYU.)
CO + Cl2 → COCl2
A + B → C
The microreactor is 20 mm long, 500 μm in diameter, and packed with catalyst particles 35 μm in diameter. The entering partial pressure of A is 231 kPa (2.29 atm), and the entering flow to each microreactor is equimolar. The molar flow rate of CO is 2 × 10–5 mol/s and the volumetric flow is 2.83 × 10–7 m3/s. The weight of catalyst in one microreactor: W = 3.5 × 10–6 kg. The reactor is kept iso-thermal at 120°C. Because the catalyst is also slightly different than the one in Figure P5-21B, the rate law is different as well:
Additional information:
α = 3.55 × 105/kg catalyst (based on properties of air and ϕ = 0.4)
k = 0.004 m6/(mol · s · kg catalyst) at 120°C
υ0 = 2.83 · 10–7 m3/s, ρ = 7 kg/m3, μ = 1.94 · 10–5 kg/m · s
Ac = 1.96 · 10–7 m2, G = 10.1 kg/m2 · s
Plot the molar flow rates FA, FB, and FC, the conversion X, and pressure ratio p along the length (i.e., catalyst weight, W) of the reactor.
Calculate the number of microreactors in parallel needed to produce 10000 kg/year phosgene.
Repeat part (a) for the case when the catalyst weight remains the same but the particle diameter is cut in half. If possible, compare your answer with part (a) and describe what you find, noting anything unusual.
How would your answers to part (a) change if the reaction were reversible with KC = 0.4 dm3/mol? Describe what you find.
What are the advantages and disadvantages of using an array of microreactors over using one conventional packed-bed reactor that provides the same yield and conversion?
Write a question that involves critical thinking, and explain why it involves critical thinking. (See Preface, Tables P-3 and P-4.)
Apply to this problem one or more of the six ideas discussed in Table P-4 in the Complete Preface-Introduction on the Web Site (http://www.umich.edu/~elements/6e/toc/Preface-Complete.pdf).
P5-22A A very proprietary industrial waste reaction, which we’ll code as A → B + S, is to be carried out in a 10-dm3 CSTR followed by a 10-dm3 PFR. The reaction is elementary, but A, which enters at a concentration of 0.001 mol/dm3 and a molar flow rate of 20 mol/min, has trouble decomposing. The specific reaction rate at 42°C (i.e., room temperature in the Mojave desert) is 0.0001 s−1. However, we don’t know the activation energy; therefore, we cannot carry out this reaction in the winter in Michigan. Consequently, this reaction, while important, is not worth your time to study. Therefore, perhaps you want to take a break and go watch a movie such as Dances with Wolves (all-time favorite of the author), Bohemian Rhapsody, A Star is Born, or Despicable Me 3. As a side note, the Jofostan Film Festival is held the last week in January in Riça, Jofostan. But don’t try to attend the Jofostan Film Festival as it’s only “A-List” celebrities such as Denzel Washington, Meryl Streep, and Sven Köttlov.
P5-23B Walter White, Jesse Pinkman, and Mike Ehrmantraut stole 1000 gal of methylamine during an episode of the TV series Breaking Bad (See Season 4, Episode 10). Shortly thereafter, Jesse and Mike decided they would get out of the cooking business and sell their shares of the methylamine. Walter wanted to keep all of the methylamine for future meth cooks and not let Jesse and Mike have their shares. Suppose Jesse and Mike decided to sabotage Walter’s cooking operation by ruining the methylamine using the following gas-phase reaction:
2 CH3NH2 ↔ (CH3)2NH + NH3
or, in short:
2A ⇄ B + C
This reaction converts the methylamine to dimethylamine, using a silica-alumina catalyst. The molar flow rate into a packed-bed reactor is 23.6 mol/s and the entering pressure is 18 atm. Assume there is no pressure drop or temperature change in the reactor. The reaction rate follows an elementary rate law in terms of partial pressure.
Write the mole balance.
Write the rate law in terms of partial pressures.
Set up a stoichiometric table for this reaction.
Write the partial pressures in terms of conversion.
Write the rate law solely in terms of conversion.
What is the equilibrium conversion, Xe?
Write out your algorithm in terms of conversion.
How many kilograms of catalyst would Jesse need to load in a PBR to obtain a conversion of 0.9*Xe? For X = 0.75 Xe?
How many kilograms of catalyst would be needed to obtain 90% of the equilibrium conversion in a fluidized bed reactor? If this weight is very, very large, what might you suggest to reduce the weight? (Ans: W = 207.2 kg catalyst)
What conversion would be achieved in a 100 kg PBR with pressure drop and α = 0.0098 kg–1? At what catalyst weight does the exit pressure fall below 1.0 atm?
Repeat (j) when pressure drop is accounted for with α = 6 × 10–4 kg–1.
While co-teaching CRE with me, PhD student Julia Faeth, created this problem using modified data from J. W. Mitchell, et al., Ind. Eng. Chem. Res. 33, 181–184 (1994).

P5-24B OEQ (Old Exam Question). Ethyl acetate is an extensively used solvent and can be formed by the vapor-phase esterification of acetic acid and ethanol.


The reaction was studied using a microporous resin as a catalyst in a packed-bed microreactor (Ind. Eng. Chem. Res., 26(2), 198(1987)). The reaction is first-order in ethanol and pseudo zero-order in acetic acid. The total volumetric feed rate is 25 dm3/min, the initial pressure is 10 atm, the temperature is 223°C, and the pressure-drop parameter, α, equals 0.01 kg–1. For an equal molar feed rate of acetic acid and ethanol, the specific reaction rate is about 1.3 dm3/kg-cat-min.
Calculate the maximum weight of catalyst that one could use and maintain an exit pressure above 1 atm. (Ans: W = 99 kg)
Write out the CRE algorithm and then solve these equations analytically to determine the catalyst weight necessary to achieve 90% conversion.
Write a Polymath program to plot and analyze X, p, and f = υ/υ0 as a function of catalyst weight down the packed-bed reactor. You can either use your analytical equations for x, p, and f or you can plot these quantities using the Polymath program.
What is the ratio of catalyst needed to achieve the last 5% (85%–90%) conversion to the weight necessary to achieve the first 5% conversion (0%–5%) in the reactor? Note: You can use the results in part (c) to also answer this part.
P5-25B The gas-phase reaction
A + B → C + D
takes place isothermally at 300 K in a packed-bed reactor in which the feed is equal molar in A and B with CA0 = 0.1 mol/dm3. The reaction is second order in A and zero order in B. Currently, 50% conversion is achieved in a reactor with 100 kg of catalysts for a volumetric flow rate 100 dm3/min. The pressure-drop parameter, α, is α = 0.0099 kg–1. If the activation energy is 10000 cal/mol, what is the specific reaction-rate constant at 400 K?
P5-26B Go to Professor Herz’s Reactor Lab on the Web at www.reactorlab.net. Click on Download and then click on the English version link. Provide the information asked and then click Download. Select Division 2, Lab 2 of The Reactor Lab concerning a packed-bed reactor (labeled PFR) in which a gas with the physical properties of air flows over spherical catalyst pellets. Perform experiments here to get a feeling for how pressure drop varies with input parameters such as reactor diameter, pellet diameter, gas flow rate, and temperature. In order to get significant pressure drop, you may need to change some of the input values substantially from those shown when you enter the lab. If you get a notice that you can’t get the desired flow, then you need to increase the inlet pressure. In Chapter 10, you will learn how to analyze the conversion results in such a reactor.
Supplementary Reading
G. KEILLOR, Pretty Good Joke Book, A Prairie Home Companion. St. Paul, MN: Highbridge Co., 2000.
J. B. BUTT, Reaction Kinetics and Reactor Design, 2nd ed. Revised and Expanded. New York: Marcel Dekker, Inc., 1999.
H. S. FOGLER, Current Fashions: What the Well-Dressed Chemical Reaction Engineer Will Be Wearing in Spring 2020. Available Fall 2025.
O. LEVENSPIEL, Chemical Reaction Engineering, 3rd ed. New York: Wiley, 1998, Chaps. 4 and 5.
Recent information on reactor design can usually be found in the following journals: Chemical Engineering Science, Chemical Engineering Communications, Industrial and Engineering Chemistry Research, Canadian Journal of Chemical Engineering, AIChE Journal, Chemical Engineering Progress.