Chapter 7
Coordinate Structures
Chapter 6 introduced a family of iterator concepts as the interface between algorithms and objects in data structures with immutable linear shape. This chapter goes beyond iterators to coordinate structures with more complex shape. We introduce bifurcate coordinates and implement algorithms on binary trees with the help of a machine for iterative tree traversal. After discussing a concept schema for coordinate structures, we conclude with algorithms for isomorphism, equivalence, and ordering.
7.1 Bifurcate Coordinates
Iterators allow us to traverse linear structures, which have a single successor at each position. While there are data structures with an arbitrary number of successors, in this chapter we study an important case of structures with exactly two successors at every position, labeled left and right. In order to define algorithms on these structures, we define the following concept:

The WeightType type function returns a type capable of counting all the objects in a traversal that uses a bifurcate coordinate. WeightType is analogous to DistanceType for an iterator type.
The predicate empty is everywhere defined. If it returns true, none of the other procedures are defined. empty is the negation of the definition-space predicate for both has_left_successor and has_right_successor. has_left_successor is the definition-space predicate for left_successor, and has_right_successor is the definition-space predicate for right_successor. In other words, if a bifurcate coordinate is not empty, has_left_successor and has_right_successor are defined; if either one of them returns true, the corresponding successor function is defined. With iterators, algorithms use a limit or count to indicate the end of a range. With bifurcate coordinates, there are many positions at which branches end. Therefore it is more natural to introduce the predicates has_left_successor and has_right_successor for determining whether a coordinate has successors.
In this book we describe algorithms on BifurcateCoordinate, where all the operations are regular. This is different from the Iterator concept, where the most fundamental algorithms, such as find, do not require regularity of successor and where there are nonregular models, such as input streams. Structures where application of left_successor and right_successor change the shape of the underlying binary tree require a concept of WeakBifurcateCoordinate, where the operations are not regular.
The shape of a structure accessed via iterators is possibly cyclic for a weak range and is a linear segment for a counted or bounded range. In order to discuss the shape of a structure accessed via bifurcate coordinates, we need a notion of reachability.
A bifurcate coordinate y is a proper descendant of another coordinate x if y is the left or right successor of x or if it is a proper descendant of the left or right successor of x. A bifurcate coordinate y is a descendant of a coordinate x if y = x or y is a proper descendant of x.
The descendants of x form a directed acyclic graph (DAG) if for all y in the descendants of x, y is not its own descendant. In other words, no sequence of successors of any coordinate leads back to itself. x is called the root of the DAG of its descendants. If the descendants of x form a DAG and are finite in number, they form a finite DAG. The height of a finite DAG is one more than the maximum sequence of successors starting from its root, or zero if it is empty.
A bifurcate coordinate y is left reachable from x if it is a descendant of the left successor of x, and similarly for right reachable.
The descendants of x form a tree if they form a finite DAG and for all y, z in the descendants of x, z is not both left reachable and right reachable from y. In other words, there is a unique sequence of successors from a coordinate to any of its descendants. The property of being a tree serves the same purpose for the algorithms in this chapter as the properties of being a bounded or counted range served in Chapter 6, with finiteness guaranteeing termination:
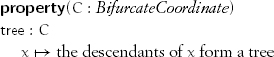
These are the recursive algorithms for computing the weight and height of a tree:


Lemma 7.1 height_recursive(x) ≤ weight_recursive (x)
height_recursive correctly computes the height of a DAG but visits each coordinate as many times as there are paths to it; this fact means that weight_recursive does not correctly compute the weight of a DAG. Algorithms for traversing DAGs and cyclic structures require marking: a way of remembering which coordinates have been previously visited.
There are three primary depth-first tree-traversal orders. All three fully traverse the left descendants and then the right descendants. Preorder visits to a coordinate occur before the traversal of its descendants; inorder visits occur between the traversals of the left and right descendants; postorder visits occur after traversing all descendants. We name the three visits with the following type definition:
enum visit { pre, in, post };
We can perform any combination of the traversals with a single procedure that takes as a parameter another procedure taking the visit together with the coordinate:

7.2 Bidirectional Bifurcate Coordinates
Recursive traversal requires stack space proportional to the height of the tree, which can be as large as the weight; this is often unacceptable for large, unbalanced trees. Also, the interface to traverse_nonempty does not allow concurrent traversal of multiple trees. In general, traversing more than one tree concurrently requires a stack per tree. If we combined a coordinate with a stack of previous coordinates, we would obtain a new coordinate type with an additional transformation for obtaining the predecessor. (It would be more efficient to use actions rather than transformations, to avoid copying the stack each time.) Such a coordinate would model the concept bidirectional bifurcate coordinate. There is a simpler and more flexible model of this concept: trees that include a predecessor link in each node. Such trees allow concurrent, constant-space traversals and make possible various rebalancing algorithms. The overhead for the extra link is usually justified.

where is_left_successor and is_right_successor are defined as follows:

Lemma 7.2 If x and y are bidirectional bifurcate coordinates,

Exercise 7.1 Would the existence of a coordinate x such that
is_left_successor (x) ![]() is_right_successor (x)
is_right_successor (x)
contradict the axioms of bidirectional bifurcate coordinates?
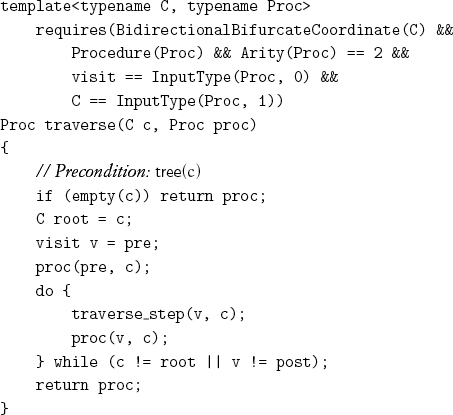
traverse_nonempty visits each coordinate three times, whether or not it has successors; maintaining this invariant makes the traversal uniform. The three visits to a coordinate always occur in the same order (pre, in, post), so given a current coordinate and the visit just performed on it, we can determine the next coordinate and the next state, using only the information from the coordinate and its predecessor. These considerations lead us to an iterative constant-space algorithm for traversing a tree with bidirectional bifurcate coordinates. The traversal depends on a machine—a sequence of statements used as a component of many algorithms:

The value returned by the procedure is the change in height. An algorithm based on traverse_step uses a loop that terminates when the original coordinate is reached on the final (post) visit:

Lemma 7.3 If reachable returns true, v = pre right before the return.
To compute the weight of a tree, we count the pre visits in a traversal:

Exercise 7.2 Change weight to count in or post visits instead of pre.
To compute the height of a tree, we need to maintain the current height and the running maximum:

The extra –1 and +1 are in case WeightType is unsigned. The code would benefit from an accumulating version of max.
We can define an iterative procedure corresponding to traverse_nonempty. We include a test for the empty tree, since it is not executed on every recursive call:
Exercise 7.3 Use traverse_step and the procedures of Chapter 2 to determine whether the descendants of a bidirectional bifurcate coordinate form a DAG.
The property readable_bounded_range for iterators says that for every iterator in a range, source is defined. An analogous property for bifurcate coordinates is

There are two approaches to extending iterator algorithms, such as find and count, to bifurcate coordinates: implementing specialized versions or implementing an adapter type.
Project 7.1 Implement versions of algorithms in Chapter 6 for bidirectional bifurcate coordinates.
Project 7.2 Design an adapter type that, given a bidirectional bifurcate coordinate type, produces an iterator type that accesses coordinates in a traversal order (pre, in, or post) specified when an iterator is constructed.
7.3 Coordinate Structures
So far, we have defined individual concepts, each of which specifies a set of procedures and their semantics. Occasionally it is useful to define a concept schema, which is a way of describing some common properties of a family of concepts. While it is not possible to define an algorithm on a concept schema, it is possible to describe structures of related algorithms on different concepts belonging to the same concept schema. For example, we defined several iterator concepts describing linear traversals and bifurcate coordinate concepts describing traversal of binary trees. To allow traversal within arbitrary data structures, we introduce a concept schema called coordinate structures. A coordinate structure may have several interrelated coordinate types, each with diverse traversal functions. Coordinate structures abstract the navigational aspects of data structures, whereas composite objects, introduced in Chapter 12, abstract storage management and ownership. Multiple coordinate structures can describe the same set of objects.
A concept is a coordinate structure if it consists of one or more coordinate types, zero or more value types, one or more traversal functions, and zero or more access functions. Each traversal function maps one or more coordinate types and/or value types into a coordinate type, whereas each access function maps one or more coordinate types and/or value types into a value type. For example, when considered as a coordinate structure, a readable indexed iterator has one value type and two coordinate types: the iterator type and its distance type. The traversal functions are + (adding a distance to an iterator) and – (giving the distance between two iterators). There is one access function: source.
7.4 Isomorphism, Equivalence, and Ordering
Two collections of coordinates from the same coordinate structure concept are isomorphic if they have the same shape. More formally, they are isomorphic if there is a one-to-one correspondence between the two collections such that any valid application of a traversal function to coordinates from the first collection returns the coordinate corresponding to the same traversal function applied to the corresponding coordinates from the second collection.
Isomorphism does not depend on the values of the objects pointed to by the coordinates: Algorithms for testing isomorphism use only traversal functions. But isomorphism requires that the same access functions are defined, or not defined, for corresponding coordinates. For example, two bounded or counted ranges are isomorphic if they have the same size. Two weak ranges of forward iterators are isomorphic if they have the same orbit structure, as defined in Chapter 2. Two trees are isomorphic when both are empty; when both are nonempty, isomorphism is determined by the following code:

Lemma 7.4 For bidirectional bifurcate coordinates, trees are isomorphic when simultaneous traversals take the same sequence of visits:

Chapter 6 contains algorithms for linear and bisection search, depending on, respectively, equality and total ordering, which are part of the notion of regularity. By inducing equality and ordering on collections of coordinates from a coordinate structure, we can search for collections of objects rather than for individual objects.
Two collections of coordinates from the same readable coordinate structure concept and with the same value types are equivalent under given equivalence relations (one per value type) if they are isomorphic and if applying the same access function to corresponding coordinates from the two collections returns equivalent objects. Replacing the equivalence relations with the equalities for the value types leads to a natural definition of equality on collections of coordinates.
Two readable bounded ranges are equivalent if they have the same size and if corresponding iterators have equivalent values:

It is straightforward to implement lexicographical_equal by passing a function object implementing equality on the value type to lexicographical_equivalent:

Two readable trees are equivalent if they are isomorphic and if corresponding coordinates have equivalent values:

For bidirectional bifurcate coordinates, trees are equivalent if simultaneous traversals take the same sequence of visits and if corresponding coordinates have equivalent values:

We can extend a weak (total) ordering to readable ranges of iterators by using lexicographical ordering, which ignores prefixes of equivalent (equal) values and considers a shorter range to precede a longer one:

It is straightforward to specialize this to lexicographical_less by passing as r a function object capturing < on the value type:

Exercise 7.4 Explain why, in lexicographical_compare, the third and fourth if statements could be interchanged, but the first and second cannot.
Exercise 7.5 Explain why we did not implement lexicographical_compare by using find_mismatch.
We can also extend lexicographical ordering to bifurcate coordinates by ignoring equivalent rooted subtrees and considering a coordinate without a left successor to precede a coordinate having a left successor. If the current values and the left subtrees do not determine the outcome, consider a coordinate without a right successor to precede a coordinate having a right successor.
Exercise 7.6 Implement bifurcate_compare_nonempty for readable bifurcate coordinates.
The readers who complete the preceding exercise will appreciate the simplicity of comparing trees based on bidirectional coordinates and iterative traversal:

We can implement bifurcate_shape_compare by passing the relation that is always false to bifurcate_compare. This allows us to sort a range of trees and then use upper_bound to find an isomorphic tree in logarithmic time.
Project 7.3 Design a coordinate structure for a family of data structures, and extend isomorphism, equivalence, and ordering to this coordinate structure.
7.5 Conclusions
Linear structures play a fundamental role in computer science, and iterators provide a natural interface between such structures and the algorithms working on them. There are, however, nonlinear data structures with their own nonlinear coordinate structures. Bidirectional bifurcate coordinates provide an example of iterative algorithms quite different from algorithms on iterator ranges. We extend the notions of isomorphism, equality, and ordering to collections of coordinates of different topologies.
