Chapter 9
Copying
This chapter introduces writable iterators, whose access functions allow the value of iterators to be modified. We illustrate the use of writable iterators with a family of copy algorithms constructed from simple machines that copy one object and update the input and output iterators. Careful specification of preconditions allows input and output ranges to overlap during copying. When two nonoverlapping ranges of the same size are mutable, a family of swapping algorithms can be used to exchange their contents.
9.1 Writability
This chapter discusses the second kind of access to iterators and other coordinate structures: writability. A type is writable if a unary procedure sink is defined on it; sink can only be used on the left side of an assignment whose right side evaluates to an object of ValueType(T):
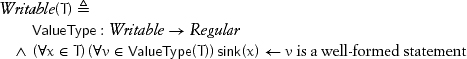
The only use of sink(x) justified by the concept Writable is on the left side of an assignment. Of course, other uses may be supported by a particular type modeling Writable.
sink does not have to be total; there may be objects of a writable type on which sink is not defined. As with readability, the concept does not provide a definition-space predicate to determine whether sink is defined for a particular object. Validity of its use in an algorithm must be derivable from preconditions.
For a particular state of an object x, only a single assignment to sink(x) can be justified by the concept Writable; a specific type might provide a protocol allowing subsequent assignments to sink(x).[1]
A writable object x and a readable object y are aliased if sink(x) and source(y) are both defined and if assigning any value v to sink(x) causes it to appear as the value of source(y):

The final kind of access is mutability, which combines readability and writability in a consistent way:

For a mutable iterator, replacing source(x) or sink(x) with deref(x) does not affect a program’s meaning or performance.
A range of iterators from a type modeling Writable and Iterator is writable if sink is defined on all the iterators in the range:
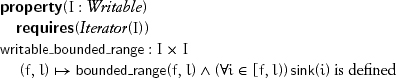
writable_weak_range and writable_counted_range are defined similarly.
With a readable iterator i, source(i) may be called more than once and always returns the same value: It is regular. This allows us to write simple, useful algorithms, such as find_if. With a writable iterator j, however, assignment to sink(j) is not repeatable: A call to successor must separate two assignments through an iterator. The asymmetry between readable and writable iterators is intentional: It does not seem to eliminate useful algorithms, and it allows models, such as output streams, that are not buffered. Nonregular successor in the Iterator concept and nonregular sink enable algorithms to be used with input and output streams and not just in-memory data structures.
A range of iterators from a type modeling Mutable and ForwardIterator is mutable if sink, and thus source and deref, are defined on all the iterators in the range. Only multipass algorithms both read from and write to the same range. Thus for mutable ranges we require at least forward iterators and we drop the requirement that two assignments to an iterator must be separated by a call to successor:
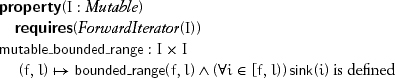
mutable_weak_range and mutable counted range are defined similarly.
9.2 Position-Based Copying
We present a family of algorithms for copying objects from one or more input ranges to one or more output ranges. In general, the postconditions of these algorithms specify equality between objects in output ranges and the original values of objects in input ranges. When input and output ranges do not overlap, it is straightforward to establish the desired postcondition. It is, however, often useful to copy objects between overlapping ranges, so the precondition of each algorithm specifies what kind of overlap is allowed.
The basic rule for overlap is that if an iterator within an input range is aliased with an iterator within an output range, the algorithm may not apply source to the input iterator after applying sink to the output iterator. We develop precise conditions, and general properties to express them, as we present the algorithms.
The machines from which we compose the copying algorithms all take two iterators by reference and are responsible for both copying and updating the iterators. The most frequently used machine copies one object and then increments both iterators:

The general form of the copy algorithms is to perform a copying step until the termination condition is satisfied. For example, copy copies a half-open bounded range to an output range specified by its first iterator:

copy returns the limit of the output range because it might not be known to the caller. The output iterator type might not allow multiple traversals, in which case if the limit were not returned, it would not be recoverable.
The postcondition for copy is that the sequence of values in the output range is equal to the original sequence of values in the input range. In order to satisfy this postcondition, the precondition must ensure readability and writability, respectively, of the input and output ranges; sufficient size of the output range; and, if the input and output ranges overlap, that no input iterator is read after an aliased output iterator is written. These conditions are formalized with the help of the property not_overlapped_forward. A readable range and a writable range are not overlapped forward if any aliased iterators occur at an index within the input range that does not exceed the index in the output range:
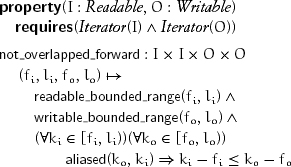
Sometimes, the sizes of the input and output ranges may be different:

While the ends of both ranges are known to the caller, returning the pair allows the caller to determine which range is smaller and where in the larger range copying stopped. Compared to copy, the output precondition is weakened: The output range could be shorter than the input range. One could even argue that the weakest precondition should be
not_overlapped_forward(fi, fi + n, fo, fo + n)
where n = min(li − fi, lo − fo).
This auxiliary machine handles the termination condition for counted ranges:

copy_n copies a half-open counted range to an output range specified by its first iterator:

The effect of copy_bounded for two counted ranges is obtained by calling copy_n with the minimum of the two sizes.
When ranges overlap forward, it still is possible to copy if the iterator types model BidirectionalIterator and thus allow backward movement. That leads to the next machine:

Since we deal with half-open ranges and start at the limit, we need to decrement before copying, which leads to copy_backward:

The postcondition for copy_backward is analogous to copy and is formalized with the help of the property not_overlapped_backward. A readable range and a writable range are not overlapped backward if any aliased iterators occur at an index from the limit of the input range that does not exceed the index from the limit of the output range:

If either of the ranges is of an iterator type modeling BidirectionalIterator, we can reverse the direction of the output range with respect to the input range by using a machine that moves backward in the output or one that moves backward in the input:

leading to the following algorithms:

reverse_copy_n and reverse_copy_backward_n are similar.
The postcondition for both reverse_copy and reverse_copy_backward is that the output range is a reversed copy of the original sequence of values of the input range. The practical, but not the weakest, precondition is that the input and output ranges do not overlap, which we formalize with the help of the property not_overlapped. A readable range and a writable range are not overlapped if they have no aliased iterators in common:
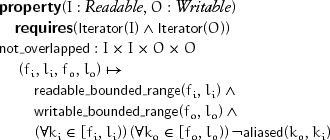
Exercise 9.1 Find the weakest preconditions for reverse_copy and its companion reverse_copy_backward.
While the main reason to introduce copy_backward as well as copy is to handle ranges that are overlapped in either direction, the reason for introducing reverse_copy_backward as well as reverse_copy is to allow greater flexibility in terms of iterator requirements.
9.3 Predicate-Based Copying
The algorithms presented so far copy every object in the input range to the output range, and their postconditions do not depend on the value of any iterator. The algorithms in this section take a predicate argument and use it to control each copying step.
For example, making the copying step conditional on a unary predicate leads to copy_select:

The worst case for nt is li − fi; the context might ensure a smaller value.
In the most common case, the predicate is applied not to the iterator but to its value:

In Chapter 8 we presented split_linked and combine_linked_nonempty operating on linked ranges of iterators. There are analogous copying algorithms:

Exercise 9.2 Write the postcondition for split_copy.
To satisfy its postcondition, a call of split_copy must ensure that the two output ranges do not overlap at all. It is permissible for either of the output ranges to overlap the input range as long as they do not overlap forward. This results in the following precondition:
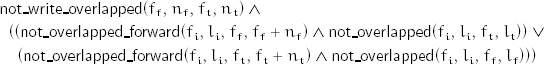
where nf and nt are upper bounds for the number of iterators not satisfying and satisfying p, respectively.
The definition of the property not_write_overlapped depends on the notion of write aliasing: two writable objects x and y such that sink(x) and sink(y) are both defined, and any observer of the effect of writes to x also observes the effect of writes to y:

That leads to the definition of not write overlapped, or writable ranges that have no aliased sinks in common:

As with select_copy, the predicate in the most common case of split_copy is applied not to the iterator but to its value:[2]
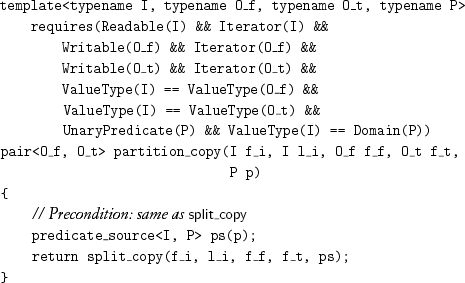
The values of each of the two output ranges are in the same relative order as in the input range; partition_copy_n is similar.
The code for combine_copy is equally simple:

For combine_copy, read overlap between the input ranges is acceptable. Furthermore, it is permissible for one of the input ranges to overlap with the output range, but such overlap cannot be in the forward direction and must be offset in the backward direction by at least the size of the other input range, as described by the property backward_offset used in the precondition of combine_copy:
![]()
where lo = fo + (li0 – fi0) + (li1 – fi1) is the limit of the output range.
The property backward_offset is satisfied by a readable range, a writable range, and an offset n ≥ 0 if any aliased iterators occur at an index within the input range that, when increased by n, does not exceed the index in the output range:

Note that not_overlapped_forward(fi, li, fo, lo) = backward_offset(fi, li, fo, lo, 0).
Exercise 9.3 Write the postcondition for combine_copy, and prove that it is satisfied whenever the precondition holds.
combine_copy_backward is similar. To ensure that the same postcondition holds, the order of the if clauses must be reversed from the order in combine_copy:

The precondition for combine_copy_backward is
![]()
where fo = lo – (li0 – fi0) + (li1 – fi1) is the first iterator of the output range.
The property forward_offset is satisfied by a readable range, a writable range, and an offset n ≥ 0 if any aliased iterators occur at an index from the limit of the input range that, increased by n, does not exceed the index from the limit of the output range:

Note that not_overlapped_backward(fi, li, fo, lo) = forward_offset(fi, li, fo, lo, 0).
Exercise 9.4 Write the postcondition for combine_copy_backward, and prove that it is satisfied whenever the precondition holds.
When the forward and backward combining copy algorithms are passed a weak ordering on the the value type, they merge increasing ranges:

Exercise 9.5 Implement combine_copy_n and combine_copy_backward_n with the appropriate return values.
Lemma 9.1 If the sizes of the input ranges are n0 and n1, merge_copy and merge_copy_backward perform n0 + n1 assignments and, in the worst case, n0 + n1 − 1 comparisons.
Exercise 9.6 Determine the best case and average number of comparisons.
Project 9.1 Modern computing systems include highly optimized library procedures for copying memory; for example, memmove and memcpy, which use optimization techniques not discussed in this book. Study the procedures provided on your platform, determine the techniques they use (for example, loop unrolling and software pipelining), and design abstract procedures expressing as many of these techniques as possible. What type requirements and preconditions are necessary for each technique? What language extensions would allow a compiler full flexibility to carry out these optimizations?
9.4 Swapping Ranges
Instead of copying one range into another, it is sometimes useful to swap two ranges of the same size: to exchange the values of objects in corresponding positions. Swapping algorithms are very similar to copying algorithms, except that assignment is replaced by a procedure that exchanges the values of objects pointed to by two mutable iterators:

Exercise 9.7 What is the postcondition of exchange_values?
Lemma 9.2 The effects of exchange_values(i, j) and exchange_values(j, i) are equivalent.
We would like the implementation of exchange_values to avoid actually constructing or destroying any objects but simply to exchange the values of two objects, so that its cost does not increase with the amount of resources owned by the objects. We accomplish this goal in Chapter 12 with a notion of underlying type.
As with copying, we construct the swapping algorithms from machines that take two iterators by reference and are responsible for both exchanging and updating the iterators. One machine exchanges two objects and then increments both iterators:

This leads to the first algorithm, which is analogous to copy:

The second algorithm is analogous to copy_bounded:

The third algorithm is analogous to copy_n:

When the ranges passed to the range-swapping algorithms do not overlap, it is apparent that their effect is to exchange the values of objects in corresponding positions. In the next chapter, we derive the postcondition for the overlapping case.
Reverse copying results in a copy in which positions are reversed from the original; reverse swapping is analogous. It requires a second machine, which moves backward in the first range and forward in the second range:

Because of the symmetry of exchange_values, reverse_swap_ranges can be used whenever at least one iterator type is bidirectional; no backward versions are needed:



9.5 Conclusions
Extending an iterator type with sink leads to writability and mutability. Although the axiom for sink is simple, the issues of aliasing and of concurrent updates—which this book does not treat—make imperative programming complicated. In particular, defining preconditions that deal with aliasing through different iterator types requires great care. Copying algorithms are simple, powerful, and widely used. Composing these algorithms from simple machines helps to organize them into a family by identifying commonalities and suggesting additional variations. Using value exchange instead of value assignment leads to an analogous but slightly smaller family of useful range-swapping algorithms.

