Chapter 5
The Black-Scholes Framework
Derivatives products have been traded in one form or another for centuries, but the development of the Black-Scholes model in the 1970s enabled financial derivatives markets to flourish by enabling volatility to be consistently priced.
Financial mathematics books generally give the derivation of the Black-Scholes formula and list the reasons why the assumptions underpinning it aren't correct in practice. Traders don't need to know how to derive the Black-Scholes formula from scratch. However, it is vital that they understand the features of the Black-Scholes framework since it is the foundation for all derivatives valuation.
Black-Scholes Stochastic Differential Equation (SDE)
The Black-Scholes framework assumes that the price of the underlying (i.e., the FX spot rate) follows a geometric Brownian motion. The Black-Scholes stochastic differential equation (SDE) is:
where ![]() is the price of the underlying (spot) at time
is the price of the underlying (spot) at time ![]() ,
, ![]() is the change in underlying at time
is the change in underlying at time ![]() ,
, ![]() and
and ![]() are continuously compounded (see Chapter 10) CCY1 and CCY2 interest rates respectively,
are continuously compounded (see Chapter 10) CCY1 and CCY2 interest rates respectively, ![]() is the volatility of the underlying's returns, generally just called “volatility,” and
is the volatility of the underlying's returns, generally just called “volatility,” and ![]() is a Brownian motion. Sometimes,
is a Brownian motion. Sometimes, ![]() is called the foreign interest rate and
is called the foreign interest rate and ![]() the domestic interest rate because, as seen in Chapters 1 and 2, P&L on standard FX contracts is naturally generated in CCY2 terms.
the domestic interest rate because, as seen in Chapters 1 and 2, P&L on standard FX contracts is naturally generated in CCY2 terms.
The left-hand side of the SDE represents relative changes in the underlying (often called “returns”). Relative changes are used within the model because as the underlying gets smaller (closer to zero), changes get smaller in absolute terms. Therefore, spot in the model can never hit zero, as in real life for FX (note that an equity underlying could go to zero).
The right-hand side of the SDE has two parts:
- Drift from the interest rate differential
- Uncertainty from the volatility of the underlying
Drift
Drift is a predictable, deterministic component that depends on the interest rate differential and the time passed:
The drift gives the no-arbitrage expected future value of spot (i.e., the forward). Forward rates for different maturities in the future define the forward path.
If ![]() (i.e., no volatility), then:
(i.e., no volatility), then:
which is solved by:
Plus recall from Chapter 1 that:
where ![]() is the forward to time
is the forward to time ![]() and
and ![]() is current spot plus note the outrageous variable change from S (spot) to F (forward).
is current spot plus note the outrageous variable change from S (spot) to F (forward).
This is important: Zero volatility does not mean that spot is static; it means that spot perfectly follows the forward path.
Under Black-Scholes assumptions, the forward path is based on current spot and constant interest rates:
- If CCY1 and CCY2 interest rates are equal, the forward path will equal spot.
- If CCY2 interest rates are higher than CCY1 interest rates, the forward path moves higher as
 increases. This is called positive drift.
increases. This is called positive drift. - If CCY1 interest rates are higher than CCY2 interest rates, the forward path moves lower as
 increases. This is called negative drift.
increases. This is called negative drift.
Within this simplified framework, at a given maturity, either the forward plus one interest rate can be used to calculate the other interest rate or two interest rates can be used to calculate the forward. All issues regarding credit risk and basis risk are ignored within this analysis.
For example: ![]() = 0% and
= 0% and ![]() = 10%. CCY2 interest rates are higher than CCY1 interest rates and therefore there is positive drift. At shorter time-scales the forward path looks linear as shown in Exhibit 5.1.
= 10%. CCY2 interest rates are higher than CCY1 interest rates and therefore there is positive drift. At shorter time-scales the forward path looks linear as shown in Exhibit 5.1.

Exhibit 5.1 Short-term forward path
Pushing the maturity out to ten years, the exponential nature of the function reveals itself in Exhibit 5.2.

Exhibit 5.2 Long-term forward path
This is important when pricing long-dated options. Exhibit 5.3 shows the USD/TRY forward path generated using constant rates to the 10yr tenor under Black-Scholes versus a market forward path generated using different interest rate instruments at different maturities.

Exhibit 5.3 USD/TRY model versus market forward path
When pricing vanilla options or any product where the payoff depends only on the spot at maturity, the forward path within the model isn't a concern so long as the forward to maturity is correct. However, the forward path is an important consideration when pricing path-dependent options, that is, options where the payoff depends not just on spot at expiry, but on the path that spot takes to get there. Many exotic options are path dependent. Consider an exotic derivative product in USD/TRY that will expire if spot ever trades above 2.5000. Using constant interest rates under Black-Scholes will generate different trading exposures than using the full market interest rate curve. Issues like this are therefore very important in practice.
Within the SDE, using full interest rate curves is equivalent to making the interest rates functions of time:
Uncertainty
The uncertainty term in the SDE is driven by a Wiener process ![]() (also called Brownian motion). A Wiener process is a continuous stochastic process with stationary independent increments. Translating:
(also called Brownian motion). A Wiener process is a continuous stochastic process with stationary independent increments. Translating:
- “Continuous” means “its path doesn't jump.”
- “Stochastic” means “it moves.”
- “Stationary” means “its probability distribution does not change over time.”
- “Independent increments” means “each change does not depend on any previous changes.”
Changes in ![]() are random with this distribution:
are random with this distribution:
In words, the change in ![]() from time
from time ![]() to time
to time ![]() is normally distributed with mean 0 and variance
is normally distributed with mean 0 and variance ![]() (i.e., standard deviation
(i.e., standard deviation ![]() ).
).
The fact that the Black-Scholes SDE is driven by a normally distributed process explains why bell-curve shapes appears repeatedly within the Black-Scholes framework.
A discrete realization of ![]() can be plotted in Excel using code shown in Exhibit 5.4 and a sample realization is plotted in Exhibit 5.5.
can be plotted in Excel using code shown in Exhibit 5.4 and a sample realization is plotted in Exhibit 5.5.

Exhibit 5.4 Excel setup for generating a realization of a Wiener process

Exhibit 5.5 A sample realization of a Wiener process
Within the Black-Scholes SDE, the Wiener process ![]() is multiplied by the volatility, meaning that, as expected, higher volatility causes spot to move more:
is multiplied by the volatility, meaning that, as expected, higher volatility causes spot to move more:
Solving the Black-Scholes SDE
The Black-Scholes SDE is solved using the magic of Itō Calculus:

The key points to note are that we've moved from regular-space into log-space and the drift has been adjusted by the Itō correction term: ![]() .
.
Furthermore, this term: ![]() is normally distributed with mean 0 and variance
is normally distributed with mean 0 and variance ![]() (i.e., standard deviation
(i.e., standard deviation ![]() ). This is important because it shows how volatility and time to expiry are linked within the distribution. Ignoring the adjusted drift, multiplying time to expiry by four changes the terminal spot distribution in the same way as doubling
). This is important because it shows how volatility and time to expiry are linked within the distribution. Ignoring the adjusted drift, multiplying time to expiry by four changes the terminal spot distribution in the same way as doubling ![]() the implied volatility.
the implied volatility.
The previous formula shows that the adjusted forward drift is the central reference point of the future log-spot distribution, which at each point is normally distributed with a wider and wider distribution over time due to increasing variance. This is shown in Exhibit 5.6.

Exhibit 5.6 Representation of the Black-Scholes framework
Because we're now in log-space, spot log returns are normally distributed. This is why log returns are always used within the realized spot volatility calculations in Chapter 17.
Understanding log-normality is important because it impacts distributions and Greek profiles particularly at higher volatility or longer maturity. For example, plotting the terminal spot distribution for 1mth EUR/USD at 8% volatility gives the standard-looking bell-shaped curve in Exhibit 5.7.
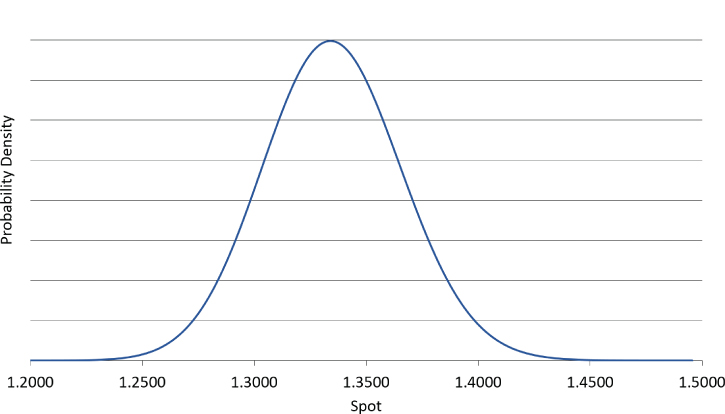
Exhibit 5.7 Terminal spot distribution at short tenor and low volatility
However, if volatility is raised to 30% and maturity is increased to five years, the shape of the distribution changes dramatically and the log-normality becomes apparent in Exhibit 5.8.

Exhibit 5.8 Terminal spot distribution at long tenor and high volatility
In a log-normal world, a spot move from 1.0 to 0.5 (log return = –0.693) is equal and opposite to a spot move from 1.0 to 2.0 (log return = +0.693). Hence log-normal distributions have a longer tail on the topside in regular spot space and never go below zero.
By taking exponentials, the SDE solution gives this analytic solution for S at time t:
The Black-Scholes formula uses constant volatility. This must be changed to the full ATM term structure when pricing path-dependent options. Within the SDE, this is equivalent to making volatility a function of time:
Consider the sharply upward-sloping implied volatility term structure in Exhibit 5.9.
Exhibit 5.9 Sample Implied Volatility Term Structure
| Tenor | Implied Volatility |
| 1mth | 5.0% |
| 2mth | 6.0% |
| 3mth | 7.0% |
| 6mth | 10.0% |
| 1yr | 15.0% |
Two realizations of ![]() can be generated using the same
can be generated using the same ![]() , one using flat volatility and the other using the implied volatility term structure. This is shown in Exhibit 5.10. Using the term structure of implied volatility leads to lower volatility at shorter tenors and higher volatility at longer tenors.
, one using flat volatility and the other using the implied volatility term structure. This is shown in Exhibit 5.10. Using the term structure of implied volatility leads to lower volatility at shorter tenors and higher volatility at longer tenors.

Exhibit 5.10 Realizations of a Wiener process using different implied volatility term structures
Within this basic Black-Scholes framework, there is only a single volatility. However, in practice, vanilla options with different maturities and strikes have different implied volatilities. In a given currency pair, the implied volatility for a given strike and expiry date is determined by the volatility surface for that pair. This idea is explored in Chapter 7.
Calculating Option Values Using Terminal Spot Distributions
Terminal spot distributions can be used to price vanilla options or any other derivative product where the payoff depends only on spot at the option maturity. The value of the option can be obtained by integrating the option payoff at maturity against the terminal spot distribution as shown in Exhibit 5.11. Intuitively, this calculation multiplies the probability of spot ending up at each point by the option payoff at that spot level. This technique is implemented in Practical B.

Exhibit 5.11 Valuing vanilla options using the terminal spot distribution
The Black-Scholes Formula
Finally, we arrive at the Black-Scholes formula itself, which gives prices for European vanilla calls and puts. The Garman and Kohlhagen (1983) formula is the FX-specific extension to the Black-Scholes formula that uses interest rates in both currencies:
where

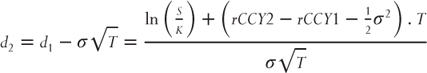
These formulas are implemented in Practical C.
The key to the derivation of the Black-Scholes formula is the assumption that option value can be continuously delta hedged at no cost. This removes all sources of risk except for volatility. The main driver behind the formula is ![]() , the cumulative normal distribution function, which gives the probability that a normally distributed variable with mean 0 and standard deviation 1 will have a value less than or equal to
, the cumulative normal distribution function, which gives the probability that a normally distributed variable with mean 0 and standard deviation 1 will have a value less than or equal to ![]() . Exhibit 5.12 shows a graph of the cumulative normal distribution function.
. Exhibit 5.12 shows a graph of the cumulative normal distribution function.

Exhibit 5.12 Cumulative normal distribution function
Even though the assumptions underpinning the Black-Scholes framework do not hold in practice, that isn't a day-to-day concern for traders. The main way in which the Black-Scholes formula itself is used is as a method of going between volatility pricing and premium pricing. It is instructive to note that the simplicity of the Black-Scholes framework is one of the key reasons why it is still in use decades after it was developed. Another reason is its extendibility; all the pricing models discussed in Chapter 19 extend Black-Scholes by relaxing different assumptions within the framework.
