3.3. Tensor Calculus

Tensor calculus is a natural tool to use when the objects at study are expressed in a specific coordinate system but have physical properties that are independent on the chosen coordinate system. Another advantage is that it gives a simple and compact notation and the rules for tensor algebra make it easy to remember even quite complex formulas. For a more detailed treatment, see [58], and for an engineering approach, see [42].

In this chapter, a simple definition of a tensor and the basic rules for manipulating tensors are given. We start with a straightforward definition:

Definition 19. An affine tensor is an object in a linear space, V, that consists of a collection of numbers that are related to a specific choice of coordinate system in V, indexed by one or several indices:

Furthermore, this collection of numbers transforms in a predefined way when a change of coordinate system in V is made; see Definition 20. The number of indices (n + m) is called the degree of the tensor. The indices may take any value from 1 to the dimension of V. The upper indices are called contravariant indices and the lower indices are called covariant indices. ▪

There are some simple conventions that have to be remembered:

- The index rule When an index appears in a formula, the formula is valid for every value of the index: a_i = 0 ⇒ a₁ = 0, a₂ = 0, ....

- The summation convention When an index appears twice in a formula, it is implicitly assumed that a summation takes place over that index: .

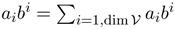- The compatibility rule A repeated index must appear once as a sub-index and once as a super-index.

- The maximum rule An index cannot be used more than twice in a term.

Definition 20. When the coordinate system in V is changed from e to ê and the points with coordinates x are changed to , according to

then the affine tensor components change according to

for lower and upper indices respectively. ▪

From this definition, the terminology for indices can be motivated, since the covariant indices covary with the basis vectors and the contravariant indices contravary with the basis vectors. It turns out that a vector (e.g., the coordinates of a point) is a contravariant tensor of degree one and that a one-form (e.g., the coordinate of a vector defining a line in ² or a hyperplane in ⁿ) is a covariant tensor of degree one.

Definition 21. The second-order tensor

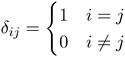
is called the Kronecker delta. When dim V = 3, the third order tensor

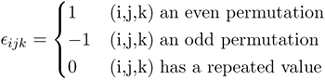
is called the Levi-Cevita epsilon.