2.4. Camera Calibration with 2D Objects: Plane-Based Technique

In this section, we describe how a camera can be calibrated using a moving plane. We first examine the constraints on the camera's intrinsic parameters provided by observing a single plane.

2.4.1. Homography between the model plane and its image

Without loss of generality, we assume the model plane is on Z = 0 of the world coordinate system. Let's denote the i-th column of the rotation matrix R by r_i. From (2.1), we have

By abuse of notation, we still use M to denote a point on the model plane, but M = [X, Y]^T, since Z is always equal to 0. In turn, . Therefore, a model point M and its image m is related by a homography H:

Equation 2.18

As is clear, the 3 × 3 matrix H is defined up to a scale factor.

2.4.2. Constraints on the intrinsic parameters

Given an image of the model plane, a homography can be estimated (see the appendix in Section 2.8). Let's denote it by H = [h₁ h₂ h₃]. From (2.18), we have

where λ is an arbitrary scalar. Using the knowledge that r₁ and r₂ are orthonormal, we have

Equation 2.19

Equation 2.20

These are the two basic constraints on the intrinsic parameters, given one homography. Because a homography has eight degrees of freedom and there are six extrinsic parameters (three for rotation and three for translation), we can only obtain two constraints on the intrinsic parameters. Note that A^–TA^–1 actually describes the image of the absolute conic [20]. Section 2.4.3 provides a geometric interpretation.

2.4.3. Geometric interpretation

We are now relating (2.19) and (2.20) to the absolute conic [22, 20].

It is not difficult to verify that the model plane, under our convention, is described in the camera coordinate system by the following equation:

where w = 0 for points at infinity and w = 1 otherwise. This plane intersects the plane at infinity at a line, and we can easily see that are two particular points on that line. Any point on it is a linear combination of these two points; that is,

Now, let's compute the intersection of the above line with the absolute conic. By definition, the point x_∞, known as the circular point [26], satisfies ; that is, (ar₁ + br₂)^T(ar₁ + br₂) = 0, or a² + b² = 0. The solution is b = ±ai, where i² = –1. That is, the two intersection points are

The significance of this pair of complex conjugate points is that they are invariant to Euclidean transformations. Their projection in the image plane is given, up to a scale factor, by

Point is on the image of the absolute conic, described by A^–TA^–1 [20]. This gives

Requiring that both real and imaginary parts be zero yields (2.19) and (2.20).

2.4.4. Closed-form solution

We now provide the details on how to effectively solve the camera calibration problem. We start with an analytical solution. This initial estimation is followed by a nonlinear optimization technique based on the maximum likelihood criterion, to be described in Section 2.4.5.

Let

Equation 2.21

Equation 2.22

Note that B is symmetric, defined by a 6D vector

Equation 2.23

Let the i-th column vector of H be h_i = [h_i1, h_i2, h_i3]^T. Then, we have

Equation 2.24

with V_ij = [h_i1h_j1, h_i1h_j2 + h_i2h_j1, h_i2h_j2, h_i3h_j1 + h_i1h_j3, h_i3h_j2 + h_i2h_j3, h_i3h_j3]^T. Therefore, the two fundamental constraints (2.19) and (2.20), from a given homography, can be rewritten as two homogeneous equations in b:

Equation 2.25

If n images of the model plane are observed, by stacking n such equations as (2.25), we have

Equation 2.26

where V is a 2n × 6 matrix. If n ≥ 3, we have, in general, a unique solution b defined up to a scale factor. If n = 2, we can impose the skewless constraint γ = 0, that is, [0, 1, 0, 0, 0, 0]b = 0, which is added as an additional equation to (2.26). (If n = 1, we can solve only two camera intrinsic parameters, e.g., α and β, assuming u₀ and v₀ are known [e.g., at the image center] and γ = 0, and that is indeed what we did in [28] for head pose determination based on the fact that eyes and mouth are reasonably coplanar. In fact, Tsai [33] already mentions that focal length from one plane is possible, but incorrectly says that aspect ratio is not.) The solution to (2.26) is well known as the eigenvector of V^TV associated with the smallest eigenvalue (equivalently, the right singular vector of V associated with the smallest singular value).

Once b is estimated, we can compute all camera intrinsic parameters as follows. The matrix B, as described in Section 2.4.4, is estimated up to a scale factor, i.e.,, B = λA^-TA with λ an arbitrary scale. Without difficulty, we can uniquely extract the intrinsic parameters from matrix B.

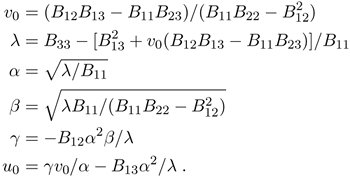
Once A is known, the extrinsic parameters for each image are readily computed. From (2.28), we have

with λ = 1/||A^–1h₁|| = 1/||A^–1h₂||. Of course, because of noise in data, the so-computed matrix R = [r₁, r₂, r₃] does not generally satisfy the properties of a rotation matrix. The best rotation matrix can then be obtained through, for example, singular value decomposition [13, 41].

2.4.5. Maximum likelihood estimation

The above solution is obtained through minimizing an algebraic distance which is not physically meaningful. We can refine it through maximum likelihood inference.

We are given n images of a model plane, and there are m points on the model plane. Assume that the image points are corrupted by independent and identically distributed noise. The maximum likelihood estimate can be obtained by minimizing the following functional:

Equation 2.27

where is the projection of point M_j in image i, according to equation (2.18). A rotation R is parameterized by a vector of three parameters, denoted by r, which is parallel to the rotation axis and whose magnitude is equal to the rotation angle. R and r are related by the Rodrigues formula [8]. Minimizing (2.27) is a nonlinear minimization problem, which is solved with the Levenberg-Marquardt algorithm as implemented in Minpack [23]. It requires an initial guess of A, {R_i, t_i|i = 1..n}, which can be obtained using the technique described in the previous section.

Desktop cameras usually have visible lens distortion, especially the radial components. We have included these while minimizing (2.27). See my technical report [41] for more details.

2.4.6. Dealing with radial distortion

Up to now, we have not considered lens distortion of a camera. However, a desktop camera usually exhibits significant lens distortion, especially radial distortion. Refer to Section 2.3.5 for distortion modeling. In this section, we consider the first two terms of radial distortion.

Estimating Radial Distortion by Alternation

As the radial distortion is expected to be small, we would expect to estimate the other five intrinsic parameters, using the technique described in Section 2.4.5, reasonably well by simply ignoring distortion. One strategy is then to estimate k₁ and k₂ after having estimated the other parameters, which will give us the ideal pixel coordinates (u, v). Then, from (2.15) and (2.16), we have two equations for each point in each image:

Given m points in n images, we can stack all equations together to obtain in total 2mn equations, or in matrix form as Dk = d, where k = [k₁, k₂]^T. The linear least-squares solution is given by

Equation 2.28

Once k₁ and k₂ are estimated, we can refine the estimate of the other parameters by solving (2.27) with replaced by (2.15) and (2.16). We can alternate these two procedures until convergence.

Complete Maximum Likelihood Estimation

Experimentally, we found the convergence of the above alternation technique is slow. A natural extension to (2.27) is then to estimate the complete set of parameters by minimizing the following functional:

Equation 2.29

where is the projection of point M_j in image i according to equation (2.18), followed by distortion according to (2.15) and (2.16). This is a nonlinear minimization problem, which is solved with the Levenberg-Marquardt algorithm as implemented in Minpack [23]. A rotation is again parameterized by a 3-vector r, as in Section 2.4.5. An initial guess of A and {R_i, t_i|i = 1, …, n} can be obtained using the technique described in Section 2.4.4 or in Section 2.4.5. An initial guess of k₁ and k₂ can be obtained with the technique described in the last paragraph or simply by setting them to 0.

2.4.7. Summary

The recommended calibration procedure is as follows:

1.	Print a pattern and attach it to a planar surface;
2.	Take a few images of the model plane under different orientations by moving either the plane or the camera;
3.	Detect the feature points in the images;
4.	Estimate the five intrinsic parameters and all the extrinsic parameters using the closed-form solution described in Section 2.4.4;
5.	Estimate the coefficients of the radial distortion by solving the linear least-squares (2.28);
6.	Refine all parameters, including lens distortion parameters, by minimizing (2.29).

There is a degenerate configuration in my technique when planes are parallel to each other. See my technical report [41] for a more detailed description.

In summary, this technique requires the camera to observe a planar pattern from only a few different orientations. Although the minimum number of orientations is two if pixels are square, we recommend four or five different orientations for better quality. We can move either the camera or the planar pattern. The motion does not need to be known, but should not be a pure translation. When the number of orientations is only two, one should avoid positioning the planar pattern parallel to the image plane. The pattern could be anything, as long as we know the metric on the plane. For example, we can print a pattern with a laser printer and attach the paper to a reasonable planar surface such as a hard book cover. We can even use a book with known size because the four corners are enough to estimate the plane homographies.

2.4.8. Experimental results

The proposed algorithm has been tested on both computer-simulated data and real data. The closed-form solution involves finding a singular value decomposition of a small 2n × 6 matrix, where n is the number of images. The nonlinear refinement within the Levenberg-Marquardt algorithm takes three to five iterations to converge. We describe in this section one set of experiments with real data when the calibration pattern is at different distances from the camera. Refer to [41] for more experimental results with both computer-simulated and real data, and to http://research.microsoft.com/~zhang/Calib/ for some experimental data and the software.

The example is shown in Figure 2.6. The camera to be calibrated is an off-the-shelf PULNiX CCD camera with 6 mm lens. The image resolution is 640x480. As can be seen in Figure 2.6, the model plane contains 9 × 9 squares with nine special dots used to identify automatically the correspondence between reference points on the model plane and square corners in images. It was printed on an A4 paper with a 600 DPI laser printer and attached to a cardboard.

Ten images of the plane were taken (six of them are shown in Figure 2.6). Five of them (Set A) were taken at close range, while the other five (Set B) were taken at a larger distance. We applied our calibration algorithm to Set A, Set B, and also to the whole set (Set A+B). The results are shown in Table 2.1. For intuitive understanding, we show the estimated angle between the image axes, , instead of the skew factor γ. We can see that the angle is very close to 90°, as expected with almost all modern CCD cameras. The camera parameters were estimated consistently for all three sets of images, except the distortion parameters with Set B. The reason is that the calibration pattern occupies only the central part of the image in Set B, where lens distortion is not significant and therefore cannot be estimated reliably.

Table 2.1. Calibration results with the images shown in Figure 2.6

image set	α	β	ϑ	u0	v0	k1	k2
A	834.01	839.86	89.95°	305.51	240.09	–0.2235	0.3761
B	836.17	841.08	89.92°	301.76	241.51	–0.2676	1.3121
A+B	834.64	840.32	89.94°	304.77	240.59	–0.2214	0.3643

2.4.9. Related work

Almost at the same time, Sturm and Maybank [31], independent from us, developed the same technique. They assumed the pixels are square (i.e., γ = 0) and have studied the degenerate configurations for plane-based camera calibration.

Gurdjos et al. [14] re-derived the plane-based calibration technique from the center line constraint.

My original implementation (only the executable) is available at http://research.microsoft.com/~zhang/calib/. Bouguet has reimplemented my technique in Matlab, which is available at http://www.vision.caltech.edu/bouguetj/calib_doc/.

In many applications, such as stereo, multiple cameras need to be calibrated simultaneously in order to determine the relative geometry between cameras. In 2000, I extended (not published) this plane-based technique to stereo calibration for my stereo-based gaze-correction project [40, 39]. The formulation is similar to (2.29). Consider two cameras, and denote the quantity related to the second camera by '. Let (R_s, t_s) be the rigid transformation between the two cameras such that (R', t') = (R, t) ○ (R_s, t_s), or more precisely, R' = RR_S and t' = Rt_s + t. Stereo calibration is then to solve A, A', k₁, k₂, , , {(R_i, t_i)|i = 1, …, n}, and (R_s, t_s) by minimizing the following functional:

Equation 2.30

subject to

In the above formulation, δ_ij = 1 if point j is visible in the first camera, and δij = 0 otherwise. Similarly, if point j is visible in the second camera. This formulation thus does not require the same number of feature points to be visible over time or across cameras. Another advantage of this formulation is that the number of extrinsic parameters to be estimated has been reduced from 12n if the two cameras are calibrated independently to 6n + 6. This is a reduction of 24 dimensions in parameter space if five planes are used.

Obviously, this is a nonlinear optimization problem. To obtain the initial guess, we first run single-camera calibration independently for each camera, and compute R_s through SVD from (i = 1, …, n) and t_s through least-squares from . Recently, a closed-form initialization technique through factorization of homography matrices is proposed in [34].