2.5. Solving Camera Calibration with 1D Objects

In this section, we describe in detail how to solve the camera calibration problem from a number of observations of a 1D object consisting of three collinear points moving around one of them [43, 44]. We consider only this minimal configuration, but it is straightforward to extend the result if a calibration object has four or more collinear points.

2.5.1. Setups with free-moving 1D calibration objects

We now examine possible setups with 1D objects for camera calibration. As already mentioned, we need to have several observations of the 1D objects. Without loss of generality, we choose the camera coordinate system to define the 1D objects; therefore, R = I and t = 0 in (2.1).

Two points with known distance

This could be the two endpoints of a stick, and we take a number of images while waving freely the stick. Let A and B be the two 3D points, and a and b be the observed image points. Because the distance between A and B is known, we only need five parameters to define A and B. For example, we need three parameters to specify the coordinates of A in the camera coordinate system, and two parameters to define the orientation of the line AB. On the other hand, each image point provides two equations according to (2.1), giving in total four equations. Given N observations of the stick, we have five intrinsic parameters and 5N parameters for the point positions to estimate, that is, the total number of unknowns is 5 + 5N. However, we have only 4N equations. Camera calibration is thus impossible.

Three collinear points with known distances

By adding an additional point, say C, the number of unknowns for the point positions still remains the same, i.e., 5+5N, because of known distances of C to A and B. For each observation, we have three image points, yielding in total 6N equations. Calibration seems to be plausible, but is in fact not. This is because the three image points for each observation must be collinear. Collinearity is preserved by perspective projection. We therefore have only five independent equations for each observation. The total number of independent equations, 5N, is always smaller than the number of unknowns. Camera calibration is still impossible.

Four or more collinear points with known distances

As seen above, when the number of points increases from two to three, the number of independent equations (constraints) increases by one for each observation. If we have a fourth point, will we have in total 6N independent equations? If so, we would be able to solve the problem because the number of unknowns remains the same, i.e., 5 + 5N, and we would have more than enough constraints if N ≥ 5. The reality is that the addition of the fourth point or even more points does not increase the number of independent equations. It will always be 5N for any four or more collinear points. This is because the cross ratio is preserved under perspective projection. With known cross ratios and three collinear points, whether they are in space or in images, other points are determined exactly.

2.5.2. Setups with 1D calibration objects moving around a fixed point

From the previous discussion, calibration is impossible with a free-moving 1D calibration object, no matter how many points on the object. Now let us examine what happens if one point is fixed. In the sequel, without loss of generality, point A is the fixed point, and a is the corresponding image point. We need three parameters, which are unknown, to specify the coordinates of A in the camera coordinate system, while image point a provides two scalar equations according to (2.1).

Two points with known distance

They could be the endpoints of a stick, and we move the stick around the endpoint that is fixed. Let B be the free endpoint and b, its corresponding image point. For each observation, we need two parameters to define the orientation of the line AB and therefore the position of B because the distance between A and B is known. Given N observations of the stick, we have five intrinsic parameters, three parameters for A and 2N parameters for the free endpoint positions to estimate; that is, the total number of unknowns is 8 + 2N. However, each observation of b provides two equations, so together with a we have in total only 2 + 2N equations. Camera calibration is thus impossible.

Three collinear points with known distances

As explained in the last subsection, by adding an additional point, say C, the number of unknowns for the point positions still remains the same: 8 + 2N. For each observation, b provides two equations, but c provides only one additional equation because of the collinearity of a, b, and c. Thus, the total number of equations is 2 + 3N for N observations. By counting the numbers, we see that if we have six or more observations, we should be able to solve camera calibration, and this is the case, as we shall show in the next section.

Four or more collinear points with known distances

Again, the number of unknowns and the number of independent equations remain the same because of invariance of cross-ratios. This said, the more collinear points we have, the more accurate camera calibration will be in practice because data redundancy can combat the noise in image data.

2.5.3. Basic equations

Refer to Figure 2.7. Point A is the fixed point in space, and the stick AB moves around A. The length of the stick AB is known to be L:

Equation 2.31

The position of point C is also known with respect to A and B, and therefore

Equation 2.32

where λ_A and λ_B are known. If C is the midpoint of AB, then λ_A = λ_B = 0.5. Points a, b, and c on the image plane are projections of space points A, B, and C respectively.

Without loss of generality, we choose the camera coordinate system to define the 1D objects; therefore, R = I and t = 0 in (2.1). Let the unknown depths for A, B, and C be z_A, z_B, and z_C, respectively. According to (2.1), we have

Equation 2.33

Equation 2.34

Equation 2.35

Substituting them into (2.32) yields

Equation 2.36

after eliminating A^–1 from both sides. By performing cross-product on both sides of the above equation with , we have

In turn, we obtain

Equation 2.37

From (2.31), we have

Substituting z_B by (2.37) gives

This is equivalent to

Equation 2.38

with

Equation 2.39

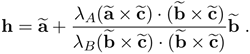
Equation (2.38) contains the unknown intrinsic parameters A and the unknown depth, z_A, of the fixed point A. It is the basic constraint for camera calibration with 1D objects. Vector h, given by (2.39), can be computed from image points and known λ_A and λ_B. Since the total number of unknowns is six, we need at least six observations of the 1D object for calibration. Note that A^–TA actually describes the image of the absolute conic [20].

2.5.4. Closed-form solution

Let

Equation 2.40

Equation 2.41

Note that B is symmetric and can be defined by a 6D vector

Equation 2.42

Let h = [h₁, h₂, h₃]^T, and x = , then equation (2.38) becomes

Equation 2.43

with

When N images of the 1D object are observed, by stacking n such equations as (2.43), we have

Equation 2.44

where V = [v₁, …, v_N]^T and 1 = [1, …, 1]^T. The least-squares solution is then given by

Equation 2.45

Once x is estimated, we can compute all the unknowns based on . Let x = [x₁, x₂, …, x₆]^T.Without difficulty, we can uniquely extract the intrinsic parameters and the depth z_A as

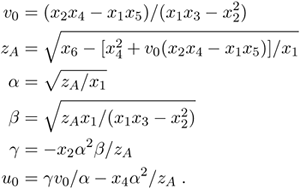
At this point, we can compute z_B according to (2.37), so points A and B can be computed from (2.33) and (2.34), while point C can be computed according to (2.32).

2.5.5. Nonlinear optimization

The above solution is obtained through minimizing an algebraic distance which is not physically meaningful. We can refine it through maximum likelihood inference.

We are given N images of the 1D calibration object, and there are three points on the object. Point A is fixed, and points B and C move around A. Assume that the image points are corrupted by independent and identically distributed noise. The maximum likelihood estimate can be obtained by minimizing the following functional:

Equation 2.46

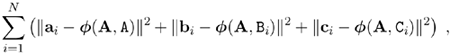
where φ(A, M) (M ∊ {A, B_i, C_i}) is the projection of point M onto the image, according to equations (2.33) to (2.35). More precisely, , where z_M is the z-component of M.

The unknowns to be estimated are

- 5 camera intrinsic parameters, α, β, γ, u₀, and v₀, that define matrix A;

- 3 parameters for the coordinates of the fixed point A;

- 2N additional parameters to define points B_i and C_i at each instant (see below for more details).

Therefore, we have in total 8 + 2N unknowns. Regarding the parameterization for B and C, we use the spherical coordinates φ and θ to define the direction of the 1D calibration object, and point B is then given by

where L is the known distance between A and B. In turn, point C is computed according to (2.32). We therefore need only two additional parameters for each observation.

Minimizing (2.46) is a nonlinear minimization problem, which is solved with the Levenberg-Marquardt algorithm, as implemented in Minpack [23]. It requires an initial guess of A, A, {B_i, C_i|i = 1, …, N}, which can be obtained using the technique described in the last subsection.

2.5.6. Estimating the fixed point

In the above discussion, we assumed that the image coordinates, a, of the fixed point A are known. We now describe how to estimate a by considering whether the fixed point A is visible in the image or not.

Invisible fixed point

The fixed point does not need to be visible in the image, and the camera calibration technique becomes more versatile without the visibility requirement. In that case, we can, for example, hang a string of small balls from the ceiling and calibrate multiple cameras in the room by swinging the string. The fixed point can be estimated by intersecting lines from different images as described below.

Each observation of the 1D object defines an image line. An image line can be represented by a 3D vector 1 = [l₁, l₂, l₃]^T, defined up to a scale factor such as a point m = [u, v]^T on the line satisfies . In the sequel, we also use (n, q) to denote line 1, where n = [l₁, l₂]^T and q = l₃. To remove the scale ambiguity, we normalize 1 such that ||1|| = 1. Furthermore, each 1 is associated with an uncertainty measure represented by a 3 x 3 covariance matrix ∧.

Given N images of the 1D object, we have N lines: {(I_i, ∧_i)|i = 1, …, N}. Let the fixed point be a in the image. Obviously, if there is no noise, we have , or . Therefore, we can estimate a by minimizing

Equation 2.47

where w_i is a weighting factor (see below). By setting the derivative of F with respect to a to 0, we obtain the solution, which is given by

The optimal weighting factor w_i in (2.47) is the inverse of the variance of , which is . Note that the weight w_i involves the unknown a. To overcome this difficulty, we can approximate w_i by 1/ trace(∧_i) for the first iteration and by recomputing w_i with the previously estimated a in the subsequent iterations. Usually two or three iterations are enough.

Visible fixed point

Since the fixed point is visible, we have N observations: {a_i|i = 1, …, N}. We can therefore estimate a by minimizing , assuming that the image points are detected with the same accuracy. The solution is simply .

The above estimation does not make use of the fact that the fixed point is also the intersection of the N observed lines of the 1D object. Therefore, a better technique to estimate a is to minimize the following function:

Equation 2.48

where V_i is the covariance matrix of the detected point a_i. The derivative of the above function with respect to a is given by

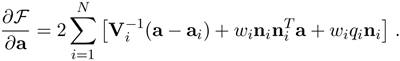
Setting it to 0 yields

If more than three points are visible in each image, the known cross-ratio provides an additional constraint in determining the fixed point.

For an accessible description of uncertainty manipulation, refer to [45].

2.5.7. Experimental results

The proposed algorithm has been tested on both computer-simulated data and real data.

Computer Simulations

The simulated camera has the following properties: α = 1000, β = 1000, γ = 0, u₀ = 320, and v₀ = 240. The image resolution is 640 x 480. A stick of 70 cm is simulated with the fixed point A at [0, 35, 150]^T. The other endpoint of the stick is B, and C is located at the halfway point between A and B. We have generated 100 random orientations of the stick by sampling θ in [π/6, 5π/6] and φ in [π, 2π] according to uniform distribution. Points A, B, and C are then projected onto the image.

Gaussian noise with 0 mean and σ standard deviation is added to the projected image points a, b, and c. The estimated camera parameters are compared with the ground truth, and we measure their relative errors with respect to the focal length α. Note that we measure the relative errors in (u₀,v₀) with respect to α, as proposed by Triggs in [32]. He pointed out that the absolute errors in (u₀, v₀) are not geometrically meaningful, while computing the relative error is equivalent to measuring the angle between the true optical axis and the estimated one.

We vary the noise level from 0.1 pixels to 1 pixel. For each noise level, we perform 120 independent trials, and the results shown in Figure 2.8 are the average. Figure 2.8a displays the relative errors of the closed-form solution, and Figure 2.8b displays those of the nonlinear minimization result. Errors increase almost linearly with the noise level. The nonlinear minimization refines the closed-form solution and produces significantly better result (with 50% less errors). At 1 pixel noise level, the errors for the closed-form solution are about 12%, while those for the nonlinear minimization are about 6%.

Real Data

For the experiment with real data, I strung three toy beads together with a stick. The beads are approximately 14 cm apart (i.e., L = 28). I then moved the stick around while trying to fix one end with the aid of a book. A video of 150 frames was recorded, and four sample images are shown in Figure 2.9. A bead in the image is modeled as a Gaussian blob in the RGB space, and the centroid of each detected blob is the image point we use for camera calibration. The proposed algorithm is therefore applied to the 150 observations of the beads, and the estimated camera parameters are provided in Table 2.2. The first row is the estimation from the closed-form solution, while the second row is the refined result after nonlinear minimization. For the image skew parameter γ, we also provide the angle between the image axes in parenthesis (it should be very close to 90°).

Table 2.2. Calibration results with real data.

Solution	α	β	γ	u0	v0
Closed-form	889.49	818.59	-0.1651 (90.01°)	297.47	234.33
Nonlinear	838.49	799.36	4.1921 (89.72°)	286.74	219.89
Plane-based	828.92	813.33	-0.0903 (90.01°)	305.23	235.17
Relative difference	1.15%	1.69%	0.52% (0.29°)	2.23%	1.84%

For comparison, we also used the plane-based calibration technique described in [42] to calibrate the same camera. Five images of a planar pattern were taken, and one of them is shown in Figure 2.10. The calibration result is shown in the third row of Table 2.2. The fourth row displays the relative difference between the plane-based result and the nonlinear solution with respect to the focal length (we use 828.92). As we can observe, the difference is about 2%.

There are several sources contributing to this difference. Besides the image noise and imprecision of the extracted data points, one source is our current rudimentary experimental setup:

- The supposed-to-be fixed point was not fixed. It slipped around on the surface.

- The positioning of the beads was done with a ruler using eye inspection. .

Considering all the factors, the proposed algorithm is very encouraging