4.4. Robust Regression
The linear EIV regression model (Section 4.2.6) is employed for the discussion of the different regression techniques. In this model, the inliers are measured as
Equation 4.105
![]()
and their true values obey the constraints
Equation 4.106
![]()
The number of inliers must be much larger than the number of free parameters of the model, n1 » p. Nothing is assumed about the n — n1 outliers.
After a robust method selects the inliers, they are often postprocessed with a nonrobust technique from the least squares (LS) family to obtain the final parameter. Therefore, we start by discussing the LS estimators. Next, the family of M-estimators is introduced, and the importance of the scale parameter related to the noise of the inliers is emphasized.
All the robust regression methods popular today in computer vision can be described within the framework of M-estimation, and thus their performance also depends on the accuracy of the scale parameter. To avoid this deficiency, we approach M-estimation in a different way and introduce the pbM-estimator, which does not require the user to provide the value of the scale.
In Section 4.2.5, it was shown that when a nonlinear EIV regression model is processed as a linear model in the carriers, the associated noise is heteroscedastic. Since the robust methods discussed in this section assume the model (4.105) and (4.106), they return biased estimates if employed for solving nonlinear EIV regression problems. However, this does not mean they should not be used! The role of any robust estimator is only to establish a satisfactory inlier/outlier dichotomy. As long as most of the inliers were recovered from the data, postprocessing with the proper nonlinear (and nonrobust) method will provide the correct estimates.
Regression in the presence of multiple structures in the data are not considered beyond the particular case of two structures in the context of structured outliers. We show why all the robust regression methods fail to handle such data once the measurement noise becomes large.
Each of the regression techniques in this section is related to one of the objective functions described in Section 4.2.2. Using the same objective function, location models can also be estimated, but we do not discuss these location estimators. For example, many of the traditional clustering methods belong to the least squares family [52, Sec. 3.3.2], or there is a close connection between the mean shift procedure and M-estimators of location [17].
4.4.1. Least squares family
We saw in Section 4.2.3 that the least squares family of estimators is not robust, since its objective function JLs (4.22) is a symmetric function in all the measurements. Therefore, in this section, we assume that the data contains only inliers; that is, n = n1.
The parameter estimates of the linear EIV regression model are obtained by solving the minimization
Equation 4.107

subject to (4.106). The minimization yields the total least squares (TLS) estimator. For an in-depth analysis of the TLS estimation, see [111]. Related problems were discussed in the 19th century [33, p. 30], though the method most frequently used today, based on the singular value decomposition (SVD) was proposed only in 1970 by Golub and Reinsch [37]. See [38] for the linear algebra background.
To solve the minimization problem (4.107), we define the n × p matrices of the measurements Y and of the true values Y0:
Equation 4.108
![]()
Then (4.107) can be rewritten as
Equation 4.109
![]()
subject to
Equation 4.110
![]()
where 1n,(0n) is a vector in Rn of all ones (zeros), and ||A||F is the Frobenius norm of the matrix A.
The parameter α is eliminated next. The data is centered by using the orthogonal projector matrix ![]() , which has the property G1n = 1n. It is easy to verify that
, which has the property G1n = 1n. It is easy to verify that
Equation 4.111

The matrix ![]() = GYo is similarly defined. The parameter estimate
= GYo is similarly defined. The parameter estimate ![]() is then obtained from the minimization
is then obtained from the minimization
Equation 4.112
![]()
subject to
Equation 4.113
![]()
The constraint (4.113) implies that the rank of the true data matrix ![]() is only p — 1 and that the true θ spans its nullspace. Indeed, our linear model requires that the true data points belong to a hyperplane in Rp, which is a (p — 1)-dimensional affine subspace. The vector θ is the unit normal to this plane.
is only p — 1 and that the true θ spans its nullspace. Indeed, our linear model requires that the true data points belong to a hyperplane in Rp, which is a (p — 1)-dimensional affine subspace. The vector θ is the unit normal to this plane.
The available measurements, however, are located nearby the hyperplane and thus the measurement matrix ![]() has full-rank p. The solution of the TLS thus is the rank p - 1 approximation of
has full-rank p. The solution of the TLS thus is the rank p - 1 approximation of ![]() . This approximation is obtained from the SVD of
. This approximation is obtained from the SVD of ![]() written as a dyadic sum:
written as a dyadic sum:
Equation 4.114

where the singular vectors ![]() , i = 1, .... n, and
, i = 1, .... n, and ![]() , j = 1,...,p provide orthonormal bases for the four linear subspaces associated with the matrix
, j = 1,...,p provide orthonormal bases for the four linear subspaces associated with the matrix ![]() [38, Sec. 2.6.2], and
[38, Sec. 2.6.2], and ![]() are the singular values of this full-rank matrix.
are the singular values of this full-rank matrix.
The optimum approximation yielding the minimum Frobenius norm for the error is the truncation of the dyadic sum (4.114) at p - 1 terms [111, p. 31]:
Equation 4.115

where the matrix ![]() contains the centered corrected measurements
contains the centered corrected measurements
![]() . These corrected measurements are the orthogonal projections of the available
. These corrected measurements are the orthogonal projections of the available ![]() on the hyperplane characterized by the parameter estimates (Figure 4.6). The TLS estimator is also known as orthogonal least squares.
on the hyperplane characterized by the parameter estimates (Figure 4.6). The TLS estimator is also known as orthogonal least squares.
The rank-one nullspace of ![]() is spanned by
is spanned by ![]() p, the right singular vector associated with the smallest singular value
p, the right singular vector associated with the smallest singular value ![]() of
of ![]() [38, p.72]. Since
[38, p.72]. Since ![]() p is a unit vector,
p is a unit vector,
Equation 4.116
![]()
The estimate of α is obtained by reversing the centering operation:
Equation 4.117
![]()
The parameter estimates of the linear EIV model can also be obtained in a different, though completely equivalent, way. We define the carrier vector x by augmenting the variables with a constant
Equation 4.118
![]()
which implies that the covariance matrix of the carriers is singular. Using the n × (p + 1) matrices
Equation 4.119
![]()
the constraint (4.110) can be written as
Equation 4.120
![]()
where the subscript 1 of this parameterization in Section 4.2.6 was dropped.
Using Lagrangian multipliers, it can be shown that the parameter estimate ![]() is the eigenvector of the generalized eigenproblem
is the eigenvector of the generalized eigenproblem
Equation 4.121
![]()
corresponding to the smallest eigenvalue λmin. This eigenproblem is equivalent to the definition of the right singular values of the matrix ![]() [38, Sec. 8.3]. The condition
[38, Sec. 8.3]. The condition ![]() is then imposed on the vector
is then imposed on the vector ![]() .
.
The first-order approximation for the covariance of the parameter estimate is [70, Sec.5.2.2]
Equation 4.122
![]()
where the pseudoinverse has to be used, since the matrix has rank p following (4.121). The estimate of the noise standard deviation is
Equation 4.123
![]()
where ![]() are the residuals. The covariances for the other parameterizations of the linear EIV model, ω2 (4.53) and ω3 (4.55), can be obtained through error propagation.
are the residuals. The covariances for the other parameterizations of the linear EIV model, ω2 (4.53) and ω3 (4.55), can be obtained through error propagation.
Note that when computing the TLS estimate with either of the two methods, special care has to be taken to execute all the required processing steps. The first approach starts with the data being centered, while in the second approach a generalized eigenproblem has to be solved. These steps are sometimes neglected in computer vision algorithms.
In the traditional linear regression model, only the variable z is corrupted by noise (4.36), and the constraint is
Equation 4.124
![]()
This model is actually valid for fewer computer vision problems (Figure 4.4) than is suggested in the literature. The corresponding estimator is the well-known (ordinary) least squares (OLS)
Equation 4.125
![]()
where
Equation 4.126

If the matrix Xo is poorly conditioned, the pseudoinverse should be used instead of the full inverse.
In the presence of significant measurement noise, using the OLS estimator when the data obeys the full EIV model (4.105) results in biased estimates [111, p. 232]. This is illustrated in Figure 4.16. The n = 30 data points are generated from the model
Equation 4.127
![]()
Figure 4.16. OLS versus TLS estimation of a linear EIV model, (a) A typical trial. (b) The scatterplot of the OLS estimates. A significant bias is present. (c) The scatterplot of the TLS estimates. The true parameter values correspond to the location marked +.

where NI(·) stands for independent, normally distributed noise. Note that the constraint is not in the Hessian normal form but
Equation 4.128
![]()
where, in order to compare the performance of the OLS and TLS estimators, the parameter θ2 was set to —1. When the traditional regression model is associated with this data, it is assumed that
Equation 4.129
![]()
and the OLS estimator (4.125) is used to find ![]() and
and ![]() . The scatterplot of the result of 100 trials is shown in Figure 4.16b, and the estimates are far away from the true values.
. The scatterplot of the result of 100 trials is shown in Figure 4.16b, and the estimates are far away from the true values.
Either TLS estimation method discussed above can be employed to find the TLS estimate. However, to eliminate the multiplicative ambiguity of the parameters, the ancillary constraint ![]() has to be used. See [111, Sec. 2.3.2]. The TLS estimates are unbiased, and the scatterplot is centered on the true values (Figure 4.16c).
has to be used. See [111, Sec. 2.3.2]. The TLS estimates are unbiased, and the scatterplot is centered on the true values (Figure 4.16c).
Throughout this section, we have tacitly assumed that the data is not degenerate, that is, the measurement matrix Y has full-rank p. Both the TLS and OLS estimators can be adapted for the rank-deficient case, though then the parameter estimates are no longer unique. Techniques similar to the ones described in this section yield minimum norm solutions. See [111, Chap. 3] for the case of the TLS estimator.
4.4.2. M-estimators
The robust equivalent of the least squares family are the M-estimators, first proposed in 1964 by Huber as a generalization of the maximum likelihood technique in which contaminations in the data distribution are tolerated. See [67] for an introduction to M-estimators and [49] for a more in-depth discussion. We focus only on the class of M-estimators most recommended for computer vision applications.
The robust formulation of (4.48) is
Equation 4.130
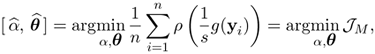
where s is a parameter that depends on σ, the (unknown) scale of the inlier noise (4.105). With a slight abuse of notation, s will also be called scale. The loss function ρ(u) satisfies the following properties: nonnegative with ρ(0) = 0, even symmetric ρ(u) = ρ(—u), and nondecreasing with |u|. For ρ(u) = u2, we obtain the LS objective function (4.107).
The different M-estimators introduced in the statistical literature differ through the distribution assumed for the data. See [5] for a discussion in the context of computer vision. However, none of these distributions will provide an accurate model in a real application. Thus, the distinctive theoretical properties of different M-estimators are less relevant in practice.
The redescending M-estimators are characterized by bounded loss functions
Equation 4.131
![]()
As will be shown below, in a redescending M-estimator, only those data points that are at distance less than s from the current fit are taken into account. This yields better outlier rejection properties than that of the M-estimators with nonredescending loss functions [69, 115].
The following class of redescending loss functions covers several important M-estimators
Equation 4.132
![]()
where d = 1, 2, 3. The loss functions have continuous derivatives up to the (d — l)-th order and a unique minimum in ρ(0) = 0.
Tukey's biweight function ρbw(u) (Figure 4.17a) is obtained for d = 3 [67, p. 295]. This loss function is widely used in the statistical literature and was known at least a century before robust estimation [40, p. 151]. See also [42, vol.1, p. 323]. The loss function obtained for d = 2 is denoted ρe(u). The case d = 1 yields the skipped mean loss function, a name borrowed from robust location estimators [89, p. 181],
Equation 4.133
![]()
Figure 4.17. Redescending M-estimators. (a) Biweight loss function. (b) The weight function for biweight. (c) Zero-one loss function.

which has discontinuous first derivative. It is often used in vision applications, such as [108].
In the objective function of any M-estimator, the geometric distances (4.46) are normalized by the scale s. Since ρ(u) is an even function, we do not need to use absolute values in (4.130). In redescending M-estimators, the scale acts as a hard rejection threshold, and thus its value is of paramount importance. For the moment, we assume that a satisfactory value is already available for s, but we return to this topic in Section 4.4.3.
The M-estimator equivalent to the total least squares is obtained following either TLS method discussed in Section 4.4.1. For example, it can be shown that instead of (4.121), the M-estimate of ω (4.120) is the eigenvector corresponding to the the smallest eigenvalue of the generalized eigenproblem,
Equation 4.134
![]()
where W ∊ Rn×n is the diagonal matrix of the nonnegative weights
Equation 4.135
![]()
Thus, in redescending M-estimators, ω(u) = 0 for |u| > 1; that is, the data points whose residual ![]() relative to the current fit is larger than the scale threshold s are discarded from the computations. The weights
relative to the current fit is larger than the scale threshold s are discarded from the computations. The weights ![]() derived from the biweight loss function are shown in Figure 4.17b. The weights derived from the ρe(u) loss function are proportional to the Epanechnikov kernel (4.79). For traditional regression, instead of (4.125), the M-estimate is
derived from the biweight loss function are shown in Figure 4.17b. The weights derived from the ρe(u) loss function are proportional to the Epanechnikov kernel (4.79). For traditional regression, instead of (4.125), the M-estimate is
Equation 4.136
![]()
The residuals ![]() in the weights wi require values for the parameter estimates. Therefore, the M-estimates can be found only by an iterative procedure.
in the weights wi require values for the parameter estimates. Therefore, the M-estimates can be found only by an iterative procedure.
M-estimation with Iterative Weighted Least Squares
1. | Obtain the initial parameter estimate |
2. | Compute the weights |
3. | Obtain the updated parameter estimates, |
4. | Determine if |
5. | Replace |
For the traditional regression, the procedure is identical. See [67, p. 306]. A different way of computing linear EIV regression M-estimates is described in [115].
The objective function minimized for redescending M-estimators is not convex, and therefore the convergence to a global minimum is not guaranteed. Nevertheless, in practice, convergence is always achieved [67, p. 307], and if the initial fit and the chosen scale value are adequate, the obtained solution is satisfactory. These two conditions are much more influential than the precise nature of the employed loss function. Note that at every iteration, all the data points regarded as inliers are processed, and thus there is no need for postprocessing, as is the case with the elemental subsets-based numerical optimization technique discussed in Section 4.2.7.
In the statistical literature, often the scale threshold s is defined as the product between ![]() , the robust estimate for the standard deviation of the inlier noise (4.105), and a tuning constant. The tuning constant is derived from the asymptotic properties of the simplest location estimator, the mean [67, p. 296]. Therefore, its value is rarely meaningful in real applications. Our definition of redescending M-estimators avoids the problem of tuning by using the inlier/outlier classification threshold as the scale parameter s.
, the robust estimate for the standard deviation of the inlier noise (4.105), and a tuning constant. The tuning constant is derived from the asymptotic properties of the simplest location estimator, the mean [67, p. 296]. Therefore, its value is rarely meaningful in real applications. Our definition of redescending M-estimators avoids the problem of tuning by using the inlier/outlier classification threshold as the scale parameter s.
The case d = 0 in (4.132) yields the zero-one loss function
Equation 4.137
![]()
shown in Figure 4.17c. The zero-one loss function is also a redescending M-estimator; however, it is no longer continuous and does not have a unique minimum in u = 0. It is only mentioned because, in Section 4.4.4, it is used to link the M-estimators to other robust regression techniques such as LMedS and RANSAC. The zero-one M-estimator is not recommended in applications. The weight function (4.135) is nonzero only at the boundary and the corresponding M-estimator has poor local robustness properties. That is, in a critical data configuration, a single data point can have a very large influence on the parameter estimates.
4.4.3. Median absolute deviation scale estimate
Access to a reliable scale parameter s is a necessary condition for the minimization procedure (4.130) to succeed. The scale s is a strictly monotonically increasing function of σ, the standard deviation of the inlier noise. Since σ is a nuisance parameter of the model, it can be estimated together with α and θ at every iteration of the M-estimation process [67, p. 307]. An example of a vision application employing this approach is [7]. However, the strategy is less robust than providing the main estimation process with a fixed-scale value [68]. In the latter case, we talk about an M-estimator with auxiliary scale [69, 100].
Two different approaches can be used to obtain the scale prior to the parameter estimation. It can be either arbitrarily set by the user, or it can be derived from the data in a pilot estimation procedure. The first approach is widely used in the robust regression techniques developed within the vision community, such as RANSAC or Hough transform. The reason is that it allows an easy way to tune a method to the available data. The second approach is often adopted in the statistical literature for M-estimators and is implicitly employed in the LMedS estimator.
The most frequently used off-line scale estimator is the median absolute deviation (MAD), which is based on the residuals ĝ(yi) relative to an initial (nonrobust TLS) fit:
Equation 4.138
![]()
where c is a constant to be set by the user. The MAD scale estimate measures the spread of the residuals around their median.
In the statistical literature, the constant in (4.138) is often taken as c = 1.4826. However, this value is used to obtain a consistent estimate for σ when all the residuals obey a normal distribution [67, p. 302]. In computer vision applications where the percentage of outliers is often high, the condition is strongly violated. In the redescending M-estimators, the role of the scale parameter s is to define the inlier/outlier classification threshold. The order of magnitude of the scale can be established by computing the MAD expression, and the rejection threshold is then set as a multiple of this value. There is no need for assumptions about the residual distribution. In [105], the standard deviation of the inlier noise ![]() was computed as 1.4826 times a robust scale estimate similar to MAD, the minimum of the LMedS optimization criterion (4.140). The rejection threshold was set at 1.965 by assuming normally distributed residuals. The result is actually three times the computed MAD value and could be obtained by setting c = 3 without any assumption about the distribution of the residuals.
was computed as 1.4826 times a robust scale estimate similar to MAD, the minimum of the LMedS optimization criterion (4.140). The rejection threshold was set at 1.965 by assuming normally distributed residuals. The result is actually three times the computed MAD value and could be obtained by setting c = 3 without any assumption about the distribution of the residuals.
The example in Figures 4.18a and 4.18b illustrates not only the importance of the scale value for M-estimation but also the danger of being locked into the nature of the residuals. The data contains 100 inliers and 75 outliers, and as expected, the initial TLS fit is completely wrong. When the scale parameter is set small by choosing for ![]() the constant c = 1.5, at convergence the final M-estimate is satisfactory (Figure 4.18a). When the scale
the constant c = 1.5, at convergence the final M-estimate is satisfactory (Figure 4.18a). When the scale ![]() is larger, c = 3.5, the optimization process converges to a local minimum of the objective function. This minimum does not correspond to a robust fit (Figure 4.18b). Note that c = 3.5 is about the value of the constant that would have been used under the assumption of normally distributed inlier noise.
is larger, c = 3.5, the optimization process converges to a local minimum of the objective function. This minimum does not correspond to a robust fit (Figure 4.18b). Note that c = 3.5 is about the value of the constant that would have been used under the assumption of normally distributed inlier noise.
Figure 4.18. Sensitivity of the M-estimation to the  scale value. Dashed line: initial TLS fit. Solid line: biweight M-estimate. (a) c = 1.5. (b) c = 3.5. (c) Overestimation of the scale in the presence of skewness. The median of the residuals is marked + under the sorted data points. The bar below corresponds to ±
scale value. Dashed line: initial TLS fit. Solid line: biweight M-estimate. (a) c = 1.5. (b) c = 3.5. (c) Overestimation of the scale in the presence of skewness. The median of the residuals is marked + under the sorted data points. The bar below corresponds to ±  computed with c = 3.
computed with c = 3.

The location estimator employed for centering the residuals in (4.138) is the median, while the MAD estimate is computed with the second, outer median. However, the median is a reliable estimator only when the distribution underlying the data is unimodal and symmetric [49, p. 29]. It is easy to see that for a heavily skewed distribution (i.e., with a long tail on one side), the median will be biased toward the tail. For such distributions, the MAD estimator severely overestimates the scale, since the 50th percentile of the centered residuals is now shifted toward the boundary of the inlier distribution. The tail is most often due to outliers, and the amount of over-estimation increases with both the decrease of the inlier/outlier ratio and the lengthening of the tail. In the example in Figure 4.18c, the inliers (at the left) were obtained from a standard normal distribution. The median is 0.73 instead of zero. The scale computed with c = 3 is ![]() = 4.08, which is much larger than 2.5, a reasonable value for the spread of the inliers. Again, c should be chosen smaller.
= 4.08, which is much larger than 2.5, a reasonable value for the spread of the inliers. Again, c should be chosen smaller.
Scale estimators that avoid centering the data were proposed in the statistical literature [88], but they are computationally intensive and their advantage for vision applications is not immediate. We must conclude that the MAD scale estimate has to be used with care in robust algorithms dealing with real data. Whenever available, independent information provided by the problem at hand should be exploited to validate the obtained scale. The influence of the scale parameter s on the performance of M-estimators can be entirely avoided by a different approach toward this family of robust estimators. This is discussed in Section 4.4.5.
4.4.4. LMedS, RANSAC, and Hough transform
The origin of these three robust techniques was described in Section 4.1. Now we show that they all can be expressed as M-estimators with auxiliary scale.
The LMedS estimator is a least k-th order statistics estimator (4.22) for k = n/2 and is the main topic of the book [89]. The LMedS estimates are obtained from
Equation 4.139
![]()
but in practice we can use
Equation 4.140
![]()
The difference between the two definitions is largely theoretical and becomes relevant only when the number of data points n is small and even, while the median is computed as the average of the two central values [89, p. 126]. Once the median is defined as the [n/2]-th order statistics, the two definitions always yield the same solution. By minimizing the median of the residuals, the LMedS estimator finds in the space of the data the narrowest cylinder containing at least half the points (Figure 4.19a). The minimization is performed with the elemental subsets-based search technique discussed in Section 4.2.7.
Figure 4.19. The difference between LMedS and RANSAC. (a) LMedS: finds the location of the narrowest band containing half the data, (b) RANSAC: finds the location of the densest band of width specified by the user.

The scale parameter s does not appear explicitly in the above definition of the LMedS estimator. Instead of setting an upper bound on the value of the scale—the inlier/outlier threshold of the redescending M-estimator-in the LMedS, a lower bound on the percentage of inliers (50%) is imposed. This eliminates the need for the user to guess the amount of measurement noise, and as long as the inliers are in absolute majority, a somewhat better robust behavior is obtained. For example, the LMedS estimator will successfully process the data in Figure 4.18a.
The relation between the scale parameter and the bound on the percentage of inliers is revealed if the equivalent condition of half the data points being outside of the cylinder is written as
Equation 4.141

where ρzo is the zero-one loss function (4.137), and the scale parameter is now regarded as a function of the residuals s[g(y1), …, g(yn)]. By defining ![]() , the LMedS estimator becomes
, the LMedS estimator becomes
Equation 4.142
![]()
The new definition of LMedS is a particular case of the S-estimators, which, while popular in statistics, are not widely know in the vision community. For an introduction to S-estimators, see [89, pp. 135-143], and for a more detailed treatment in the context of EIV models, see [115]. Let ŝ be the minimum of s in (4.142). Then, it can be shown that
Equation 4.143

and thus the S-estimators are in fact M-estimators with auxiliary scale.
The value of ŝ can also be used as a scale estimator for the noise corrupting the inliers. All the observations made in Section 4.4.3 remain valid. For example, when the inliers are no longer the absolute majority in the data, the LMedS fit is incorrect, and the residuals used to compute ŝ are not reliable.
The RANSAC estimator predates the LMedS [26]. Since the same elemental subsets-based procedure is used to optimize their objective function, sometimes the two techniques were mistakenly considered to be very similar (e.g., [74]). However, their similarity should be judged examining the objective functions and not the way the optimization is implemented. In LMedS, the scale is computed from a condition set on the percentage of inliers (4.142). In RANSAC, the following minimization problem is solved
Equation 4.144

That is, the scale is provided by the user. This is a critical difference. Note that (4.144) is the same as (4.30). Since it is relatively easy to tune RANSAC to the data, it can also handle situations in which LMedS would already fail due to the large percentage of outliers (Figure 4.19b). Today RANSAC replaced LMedS in most vision applications, [65, 83, 107], for example.
The use of the zero-one loss function in both LMedS and RANSAC yields very poor local robustness properties, as illustrated in Figure 4.20, an example inspired by [2]. The n = 12 data points appear to be a simple case of robust linear regression for which the traditional regression model (4.37) was used. The single outlier on the right corrupts the least squares (OLS) estimator. The LMedS estimator, however, succeeds in recovering the correct fit (Figure 4.20a), and the OLS postprocessing of the points declared inliers (Final) does not yield any further change. The data in Figure 4.20b seems to be the same, but now the LMedS, and therefore the postprocessing, completely failed. Actually, the difference between the two data sets is that the point (6, 9.3) was moved to (6, 9.2).
Figure 4.20. The poor local robustness of the LMedS estimator. The difference between the data sets in (a) and (b) is that the point (6, 9.3) was moved to (6, 9.2).

The configuration of this data, however, is a critical one. The six points in the center can be grouped either with the points that appear to be also inliers (Figure 4.20a) or with the single outlier on the right (Figure 4.20b). In either case, the grouping yields an absolute majority of points, which is preferred by LMedS. There is a hidden bimodality in the data, and as a consequence, a delicate equilibrium exists between the correct and the incorrect fit.
In this example, the LMedS minimization (4.140) seeks the narrowest band containing at least six data points. The width of the band is measured along the z axis, and its boundary is always defined by two of the data points [89, p. 126]. This is equivalent to using the zero-one loss function in the optimization criterion (4.143). A small shift of one of the points thus can change to which fit the value of the minimum in (4.140) corresponds to. The instability of the LMedS is discussed in a practical setting in [45], while more theoretical issues are addressed in [23]. A similar behavior is also present in RANSAC due to (4.144).
For both LMedS and RANSAC, several variants were introduced in which the zero-one loss function is replaced by a smooth function. Since more points then have nonzero weights in the optimization, the local robustness properties of the estimators improve. The least trimmed squares (LTS) estimator [89, p. 132]
Equation 4.145

minimizes the sum of squares of the k smallest residuals, where k has to be provided by the user. Similar to LMedS, the absolute values of the residuals can also be used.
In the first smooth variant of RANSAC, the zero-one loss function was replaced with the skipped mean (4.133) and was called MSAC [108]. Recently, the same loss function was used in a maximum a posteriori formulation of RANSAC, the MAPSAC estimator [104]. A maximum likelihood motivated variant, the MLESAC [106], uses a Gaussian kernel for the inliers. Guided sampling is incorporated into the IMPSAC version of RANSAC [104]. In every variant of RANSAC, the user has to provide a reasonably accurate scale value for a satisfactory performance.
The use of zero-one loss function is not the only (or main) cause of the failure of LMedS (or RANSAC). In Section 4.4.7, we show that there is a more general problem in applying robust regression methods to multistructured data.
The only robust method designed to handle multistructured data is the Hough transform. The idea of Hough transform is to replace the regression problems in the input domain with location problems in the space of the parameters. Then, each significant mode in the parameter space corresponds to an instance of the model in the input space. There is a huge literature dedicated to every conceivable aspect of this technique. The survey papers [50, 62, 81] contain hundreds of references.
Since we are focusing here on the connection between the redescending M-estimators and the Hough transform, only the randomized Hough transform (RHT) will be considered [56]. Their equivalence is the most straightforward, but the same equivalence also exists for all the other variants of the Hough transform. The feature space in RHT is built with elemental subsets, and thus we have a mapping from p data points to a point in the parameter space.
Traditionally, the parameter space is quantized into bins; that is, it is an accumulator. The sbins containing the largest number of votes yield the parameters of the significant structures in the input domain. This can be described formally as
Equation 4.146

where kzo(u) = 1−ρzo(u) and ![]() define the size (scale) of a bin along each parameter coordinate. The index k stands for the different local maxima. Note that the parameterization uses the polar angles, as discussed in Section 4.2.6.
define the size (scale) of a bin along each parameter coordinate. The index k stands for the different local maxima. Note that the parameterization uses the polar angles, as discussed in Section 4.2.6.
The definition (4.146) is that of a redescending M-estimator with auxiliary scale, where the criterion is a maximization instead of a minimization. The accuracy of the scale parameters is a necessary condition for a satisfactory performance, an issue widely discussed in the Hough transform literature. The advantage of distributing the votes around adjacent bins was recognized early [101]. Later the equivalence with M-estimators was also identified, and the zero-one loss function is often replaced with a continuous function [61, 60, 79].
In this section, we showed that all the robust techniques popular in computer vision can be reformulated as M-estimators. In Section 4.4.3, we emphasized that the scale has a crucial influence on the performance of M-estimators. In the next section, we remove this dependence by approaching the M-estimators in a different way.
4.4.5. The pbM-estimator
The minimization criterion (4.130) of the M-estimators is rewritten as
Equation 4.147

where K(u) is called the M-kernel function. Note that for a redescending Mestimator, k(u) = 0 for |u| > 1 (4.131). The positive normalization constant cρ assures that K(u) is a proper kernel (4.68).
Consider the unit vector θ defining a line through the origin in RP. The projections of the n data points yi on this line have the 1D (intrinsic) coordinates ![]() . Following (4.67), the density of the set of points xi, i = 1,..., n, estimated with the kernel K(u) and the bandwidth
. Following (4.67), the density of the set of points xi, i = 1,..., n, estimated with the kernel K(u) and the bandwidth ![]() , is
, is
Equation 4.148

Comparing (4.147) and (4.148), we can observe that if K(u) is taken as the kernel function, and ![]() is substituted for the scale s, the M-estimation criterion becomes
is substituted for the scale s, the M-estimation criterion becomes
Equation 4.149
![]()
Equation 4.150
![]()
Given the M-kernel k(u), the bandwidth parameter ![]() can be estimated from the data according to (4.76). Since, as will be shown below, the value of the bandwidth has a weak influence on the the result of the M-estimation, for the entire family of redescending loss functions (4.132), we can use
can be estimated from the data according to (4.76). Since, as will be shown below, the value of the bandwidth has a weak influence on the the result of the M-estimation, for the entire family of redescending loss functions (4.132), we can use
Equation 4.151
![]()
The MAD estimator is employed in (4.151), but its limitations (Section 4.4.3) are of less concern in this context. Also, it is easy to recognize when the data is not corrupted, since the MAD expression becomes too small. In this case, instead of the density estimation, most often a simple search over the projected points suffices.
The geometric interpretation of the new definition of M-estimators is similar to that of the LMedS and RANSAC techniques shown in Figure 4.19. The closer the projection direction is to the normal of the linear structure, the tighter the projected inliers are grouped which increases the mode of the estimated density (Figure 4.21). Again, a cylinder having the highest density in the data has to be located. The new approach is called projection-based M-estimator, or pbM-estimator.
Figure 4.21. M-estimation through projection pursuit. When the data in the rectangle is projected orthogonally on different directions (a), the mode of the estimated density is smaller for an arbitrary direction (b) than for the direction of the normal to the linear structure (c).

The relations (4.149) and (4.150) are the projection pursuit definition of an M-estimator. Projection pursuit was proposed by Friedman and Tukey in 1974 [30] to solve data analysis problems by seeking "interesting" low-dimensional projections of the multidimensional data. The informative value of a projection is measured with a projection index, such as the quantity inside the brackets in (4.149). The papers [48, 54] survey all the related topics. It should be emphasized that in the projection pursuit literature, the name projection pursuit regression refers to a technique different from ours. There, a nonlinear additive model is estimated by adding a new term to the model after each iteration; see, for example, [44, Sec. 11.2].
When in the statistical literature a linear regression problem is solved through projection pursuit, either nonrobustly [20] or robustly [89, p. 143], the projection index is a scale estimate. Similar to the S-estimators, the solution is obtained by minimizing the scale, now over the projection directions. The robust scale estimates, like the MAD (4.138) or the median of the absolute value of the residuals (4.142), however, have severe deficiencies for skewed distributions, as discussed in Section 4.4.3. Thus, their use as a projection index will not guarantee a better performance than that of the original implementation of the regression technique.
Projections were employed before in computer vision. In [80], a highly accurate implementation of the Hough transform was achieved by using local projections of the pixels onto a set of directions. Straight edges in the image were then found by detecting the maxima in the numerically differentiated projections. The L2E estimator, proposed recently in the statistical literature [91], solves a minimization problem similar to the kernel density estimate formulation of M-estimators; however, the focus is on the parametric model of the inlier residual distribution.
The critical parameter of the redescending M-estimators is the scale s, the inlier/outlier selection threshold. The novelty of the pbM-estimator is the way the scale parameter is manipulated. The pbM-estimator avoids the need of M-estimators for an accurate scale prior to estimation by using the bandwidth ![]() as scale during the search for the optimal projection direction. The bandwidth being an approximation of the AMISE optimal solution (4.75) tries to preserve the sensitivity of the density estimation process as the number of data points n becomes large. This is the reason for the n-1/5 factor in (4.151). Since
as scale during the search for the optimal projection direction. The bandwidth being an approximation of the AMISE optimal solution (4.75) tries to preserve the sensitivity of the density estimation process as the number of data points n becomes large. This is the reason for the n-1/5 factor in (4.151). Since ![]() is the outlier rejection threshold at this stage, a too small value increases the probability of incorrectly assigning the optimal projection direction to a local alignment of points. Thus, it is recommended that once n becomes large, say n > 103, the computed bandwidth value is slightly increased by a factor that is monotonic in n.
is the outlier rejection threshold at this stage, a too small value increases the probability of incorrectly assigning the optimal projection direction to a local alignment of points. Thus, it is recommended that once n becomes large, say n > 103, the computed bandwidth value is slightly increased by a factor that is monotonic in n.
After the optimal projection direction ![]() is found, the actual inlier/outlier dichotomy of the data is defined by analyzing the shape of the density around the mode. The nearest local minima on the left and on the right correspond in Rp, the space of the data, to the transition between the inliers belonging to the sought structure (which has a higher density) and the background clutter of the outliers (which has a lower density). The locations of the minima define the values α1 < α2. Together with
is found, the actual inlier/outlier dichotomy of the data is defined by analyzing the shape of the density around the mode. The nearest local minima on the left and on the right correspond in Rp, the space of the data, to the transition between the inliers belonging to the sought structure (which has a higher density) and the background clutter of the outliers (which has a lower density). The locations of the minima define the values α1 < α2. Together with ![]() they yield the two hyperplanes in Rp separating the inliers from the outliers. Note that the equivalent scale of the M-estimator is s = α2 - α1 and that the minima may not be symmetrically located relative to the mode.
they yield the two hyperplanes in Rp separating the inliers from the outliers. Note that the equivalent scale of the M-estimator is s = α2 - α1 and that the minima may not be symmetrically located relative to the mode.
The 2D data in the example in Figure 4.22a contains 100 inliers and 500 outliers. The density of the points projected on the direction of the true normal (Figure 4.22b) has a sharp mode. Since the pbM-estimator deals only with 1D densities, there is no need to use the mean shift procedure (Section 4.3.3) to find the modes, and a simple heuristic suffices to define the local minima if they are not obvious.
Figure 4.22. Determining the inlier/outlier dichotomy through the density of the projected data, (a) 2D data. Solid line: optimal projection direction. Dashed lines: boundaries of the detected inlier region, (b) The kernel density estimate of the projected points. Vertical dashed lines: the left and right local minima. The bar at the top is the scale  computed with c = 3. The bar below is
computed with c = 3. The bar below is  , the size of the kernel support. Both are centered on the mode.
, the size of the kernel support. Both are centered on the mode.

The advantage of the pbM-estimator arises from using a more adequate scale in the optimization. In our example, the ![]() scale estimate based on the TLS initial fit (to the whole data) and computed with c = 3 is about 10 times larger than
scale estimate based on the TLS initial fit (to the whole data) and computed with c = 3 is about 10 times larger than ![]() , the bandwidth computed for the optimal projection direction (Figure 4.22b). When a redescending M-estimator uses ŝmad, the optimization of the objective function is based on a too large band, which almost certainly leads to a snonrobust behavior.
, the bandwidth computed for the optimal projection direction (Figure 4.22b). When a redescending M-estimator uses ŝmad, the optimization of the objective function is based on a too large band, which almost certainly leads to a snonrobust behavior.
Sometimes the detection of the minima can be fragile. See the right minimum in Figure 4.22b. A slight change in the projected location of a few data points could have changed this boundary to the next, much more significant local minimum. However, this sensitivity is tolerated by the pbM-estimator. First, by the nature of the projection pursuit, many different projections are investigated, and thus it is probable that at least one satisfactory band is found. Second, from any reasonable inlier/outlier dichotomy of the data, postprocessing of the points declared inliers (the region bounded by the two hyperplanes in Rp) can recover the correct estimates. Since the true inliers are, with high probability, the absolute majority among the points declared inliers, the robust LTS estimator (4.145) can now be used.
The significant improvement in outlier tolerance of the pbM-estimator was obtained at the price of replacing the iterative weighted least squares algorithm of the traditional M-estimation with a search in Rp for the optimal projection direction ![]() . This search can be efficiently implemented using the simplex-based technique discussed in Section 4.2.7.
. This search can be efficiently implemented using the simplex-based technique discussed in Section 4.2.7.
A randomly selected p-tuple of points (an elemental subset) defines the projection direction θ, from which the corresponding polar angles β are computed (4.52). The vector β is the first vertex of the initial simplex in Rp-1. The remaining p - I vertices are then defined as
Equation 4.152
![]()
where ek ∊ Rp-1 is a vector of 0-s except a I in the k-th element, and γ is a small angle. While the value of γ can depend on the dimension of the space, using a constant value such as γ = π/12 seems to suffice in practice. Because θ is only a projection direction, during the search, the polar angles are allowed to wander outside the limits, assuring a unique mapping in (4.52). The simplex-based maximization of the projection index (4.149) does not have to be extremely accurate, and the number of iterations in the search should be relatively small.
The projection-based implementation of the M-estimators is summarized below.
The pbM-estimator
- Repeat N times:
1.Choose an elemental subset (p-tuple) by random sampling.2.Compute the TLS estimate of 6.3.Build the initial simplex in the space of polar angles β.4.Perform a simplex-based direct search to find the local maximum of the projection index.- Find the left and right local minima around the mode of the density corresponding to the largest projection index.
- Define the inlier/outlier dichotomy of the data. Postprocess the inliers to find the final estimates of α and θ.
4.4.6. Applications
The superior outlier tolerance of the pbM-estimator relative to other robust techniques is illustrated with two experiments. The percentage of inliers in the data is assumed unknown and can be significantly less than that of the outliers. Therefore, the LMedS estimator cannot be applied. It is shown in [106] that MLESAC and MSAC have very similar performance and are superior to RANSAC. We have compared RANSAC and MS AC with the pbM-estimator.
In both experiments, ground truth was available, and the true standard deviation of the inliers σt could be computed. The output of any robust regression is the inlier/outlier dichotomy of the data. Let the standard deviation of the points declared inliers measured relative to the true fit be ![]() . The performance of the different estimators was compared through the ratio
. The performance of the different estimators was compared through the ratio ![]() . For a satisfactory result, this ratio should be very close to one.
. For a satisfactory result, this ratio should be very close to one.
The same number of computational units is used for all the techniques. A computational unit is either processing of one elemental subset (RANSAC) or one iteration in the simplex-based direct search (pbM). The number of iterations in a search was restricted to 25, but often it ended earlier. Thus, the amount of computation attributed to the pbM-estimator is an upper bound.
In the first experiment, the synthetic data contained 100 inlier points obeying an 8D linear EIV regression model (4.106). The measurement noise was normally distributed with covariance matrix 52I8. A variable percentage of outliers was uniformly distributed within the bounding box of the region occupied in R8 by the inliers. The number of computational units was 5000; that is, RANSAC used 5000 elemental subsets while the pbM-estimator initiated 200 local searches. For each experimental condition, 100 trials were run. The true sample standard deviation of the inliers σt was computed in each trial.
The scale provided to RANSAC was the ![]() , based on the TLS fit to the data and computed with c = 3. The same scale was used for MS AC. However, in an optimal setting, MSAC was also run with the scale Sopt = 1.96σt. Note that this information is not available in practice! The graphs in Figure 4.23 show that for any percentage of outliers, the pbM-estimator performs at least as well as MSAC tuned to the optimal scale. This superior performance is obtained in a completely unsupervised fashion. The only parameters used by the pbM-estimator are the generic normalized amplitude values needed for the definition of the local minima. They do not depend on the data or on the application.
, based on the TLS fit to the data and computed with c = 3. The same scale was used for MS AC. However, in an optimal setting, MSAC was also run with the scale Sopt = 1.96σt. Note that this information is not available in practice! The graphs in Figure 4.23 show that for any percentage of outliers, the pbM-estimator performs at least as well as MSAC tuned to the optimal scale. This superior performance is obtained in a completely unsupervised fashion. The only parameters used by the pbM-estimator are the generic normalized amplitude values needed for the definition of the local minima. They do not depend on the data or on the application.
Figure 4.23. RANSAC versus pbM-estimator. The relative standard deviation of the residuals function of the percentage of outliers. Eight-dimensional synthetic data. The employed scale threshold: RANSAC -  ; MSACm -
; MSACm - 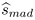 ; MSACo - sopt. The pbM-estimator has no tuning parameter. The vertical bars mark one standard deviation from the mean.
; MSACo - sopt. The pbM-estimator has no tuning parameter. The vertical bars mark one standard deviation from the mean.

In the second experiment, two far-apart frames from the corridor sequence (Figures 4.24a and 4.24b) were used to estimate the epipolar geometry from point correspondences. As was shown in Section 4.2.5, this is a nonlinear estimation problem, and therefore the role of a robust regression estimator based on the linear EIV model is restricted to selecting the correct matches. Subsequent use of a nonlinear (and nonrobust) method can recover the unbiased estimates. Several such methods are discussed in [116].
Figure 4.24. Estimating the epipolar geometry for two frames of the corridor sequence. (a) and (b) The input images with the points used for correspondences marked. (c) Histogram of the residuals from the ground truth. (d) Histogram of the inliers.

The Harris corner detector [110, Sec. 4.3] was used to establish the correspondences, from which 265 point pairs were retained. The histogram of the residuals computed as orthogonal distances from the ground-truth plane in 8D is shown in Figure 4.24c. The 105 points in the central peak of the histogram were considered the inliers (Figure 4.24d). Their standard deviation was σt = 0.88.
The number of computational units was 15000; that is, the pbM-estimator used 600 searches. Again, MSAC was tuned to either the optimal scale Sopt or to the scale derived from the MAD estimate, ![]() . The number of true inliers among the points selected by an estimator and the ratio between the standard deviation of the selected points and that of the true inlier noise are shown in the table below.
. The number of true inliers among the points selected by an estimator and the ratio between the standard deviation of the selected points and that of the true inlier noise are shown in the table below.
| selected points/true inliers | ||
|---|---|---|
| MSAC (smad) | 219/105 | 42.32 |
| MSAC (sopt) | 98/87 | 1.69 |
| pbM | 95/88 | 1.36 |
The pbM-estimator successfully recovers the data of interest and behaves like an optiSmally tuned technique from the RANSAC family. However, in practice, the tuning information is not available.
4.4.7. Structured outliers
The problem of multistructured data is not considered in this chapter, but a discussion of robust regression cannot be complete without mentioning the issue of structured outliers. This is a particular case of multistructured data, when only two structures are present and the example shown in Figure 4.3 is a typical case. For such data, once the measurement noise becomes significant, all the robust techniques-M-estimators (including the pbM-estimator), LMedS and RANSAC-behave similarly to the nonrobust least squares estimator. This was first observed for the LMedS [77] and was extensively analyzed in [97]. Here we describe a more recent approach [9].
The true structures in Figure 4.3b are horizontal lines. The lower one contains 60 points and the upper one 40 points. Thus, a robust regression method should return the lower structure as inliers. The measurement noise was normally distributed with covariance σ2I2, σ = 10. In Section 4.4.4, it was shown that all robust techniques can be regarded as M-estimators. Therefore, we consider the expression
Equation 4.153

which defines a family of curves parameterized in α and β of the line model (4.54) and in the scale s. The envelope of this family,
Equation 4.154
![]()
represents the value of the M-estimation minimization criterion (4.130) as a function of scale.
By definition, for a given value of s, the curve ∊(s; α, β) can be only above (or touching) the envelope. The comparison of the envelope with a curve ∊(s; α, β) describes the relation between the employed α, β and the parameter values minimizing (4.153). Three sets of line parameters were investigated using the zero-one (Figure 4.25a) and the Biweight (Figure 4.25b) loss functions: the true parameters of the two structures (a = 50, 100; β = π/2) and the least squares parameter estimates (αls, βls)- The LS parameters yield a line similar to the one in Figure 4.3b, a nonrobust result.
Figure 4.25. Dependence of ∊(s; α, β) on the scale s for the data in Figure 4.3b. (a) Zero-one loss function, (b) Biweight loss function, (c) The top left region of (a), (d) The top left region of (b). Solid line: envelope ∊min (s). Dashed line: true parameters of the lower structure. Dotdashed line: true parameters of the upper structure. Dotted line: least squares fit parameters.

Consider the case of zero-one loss function and the parameters of the lower structure (dashed line in Figure 4.25a). For this loss function, ∊(s; 50, π/2) is the percentage of data points outside the horizontal band centered on y2 = 50 and with half-width s. As expected, the curve has a plateau around ∊ = 0.4 corresponding to the band having one of its boundaries in the transition region between the two structures. Once the band extends into the second structure, ∊(s; 50, π/2) further decreases. The curve, however, is not only always above the envelope, but most often also above the curve ∊(s; αLS, βLS)- See the magnified area of small scales in Figure 4.25c.
For a given value of the scale (as in RANSAC), a fit similar to least squares will be preferred, since it yields a smaller value for (4.153). The measurement noise being large, a band containing half the data (as in LMedS) corresponds to a scale s > 12, the value around which the least squares fit begins to dominate the optimization (Figure 4.25a). As a result, the LMedS will always fail (Figure 4.3b). Note also the very narrow range of scale values (around s = 10) for which ∊(s; 50, π/2) is below ∊(s; αLS,βLS). It shows how accurately the user must tune an estimator in the RANSAC family for a satisfactory performance.
The behavior for the biweight loss function is identical, only the curves are smoother due to the weighted averages (Figures 4.25b and 4.25d). When the noise corrupting the structures is small-in Figure 4.3a it is σ = 2—the envelope and the curve ∊(s; 50, π/2) overlap for s < 8, which suffices for the LMedS criterion. See [9] for details.
We can conclude that multistructured data has to be processed first by breaking it into parts in which one structure dominates. The technique in [8] combines several of the procedures discussed in this chapter. The sampling was guided by local data density; it was assumed that the structures and the background can be roughly separated by a global threshold on nearest neighbor distances. The pbM-estimator was employed as the estimation module, and the final parameters were obtained by applying adaptive mean shift to a feature space. The technique had a Hough transform flavor, though no scale parameters were required. The density assumption, however, may fail when the structures are defined by linearizing a nonlinear problem, as is often the case in 3D vision. Handling such multistructured data embedded in a significant background clutter remains an open question.
