
We can also equivalently think of this as going around the axis -A°. Negative
angles move things around clockwise.
sin(0° - A) = sin(A)
cos(0° - A) = -cos(A)
tan(0° - A) = -tan(A)
Finally, if we kept going, and went around 360°, we would come right back to
where we started. Adding 360° to any angle gives you all the same values for
sine, cosine, tangent, and all the other ratios. This means that it is very handy
to use these functions for things that are going around in circles, or that
repeat somehow.
Now that we know how sine, cosine, and tangent work for angles more
than 90 degrees, we can graph them for any angle. You can get values for
these ratios either with a button on your calculator or by pasting something
into Google for a calculation. However, Google expects angles in radians,
not degrees, so you need to convert first, as we described in the sidebar
“Degrees, Radians, and Pi” earlier in this chapter.
In Figure 6-18, we see the sine (red curve) and cosine(green) are gentle
curves as the angle A increases (horizontal axis), with the signs of each of
the ratios varying as shown, repeating the pattern each 360°. The tangent
is shown in blue. Note that since tangent involves dividing by cosine, it
FIGURE 618: Sine(red), cosine(green) and tangent(blue) for
angles from -360° to 360°
FIGURE 617: Our original triangle reflected across the x-axis
Make: Geometry 117
Geometry_Chapter10_v15.indd 117Geometry_Chapter10_v15.indd 117 6/23/2021 9:09:52 AM6/23/2021 9:09:52 AM
approaches infinity when cosine approaches zero, at angles approaching 90°
and 180°.
However, since the tangent is calculated as the opposite side divided by the
adjacent side, as the angle goes to 90° the opposite side gets very big, and
the adjacent side gets very small. As the adjacent side goes to zero, the
tangent gets infinitely big (and ultimately is indeterminate, as we mentioned
earlier in the chapter). The same thing happens, in the negative direction, at
270°. You can play with the hypotenuse model we showed you earlier in this
section to prove this to yourself as the angle goes to 90°.
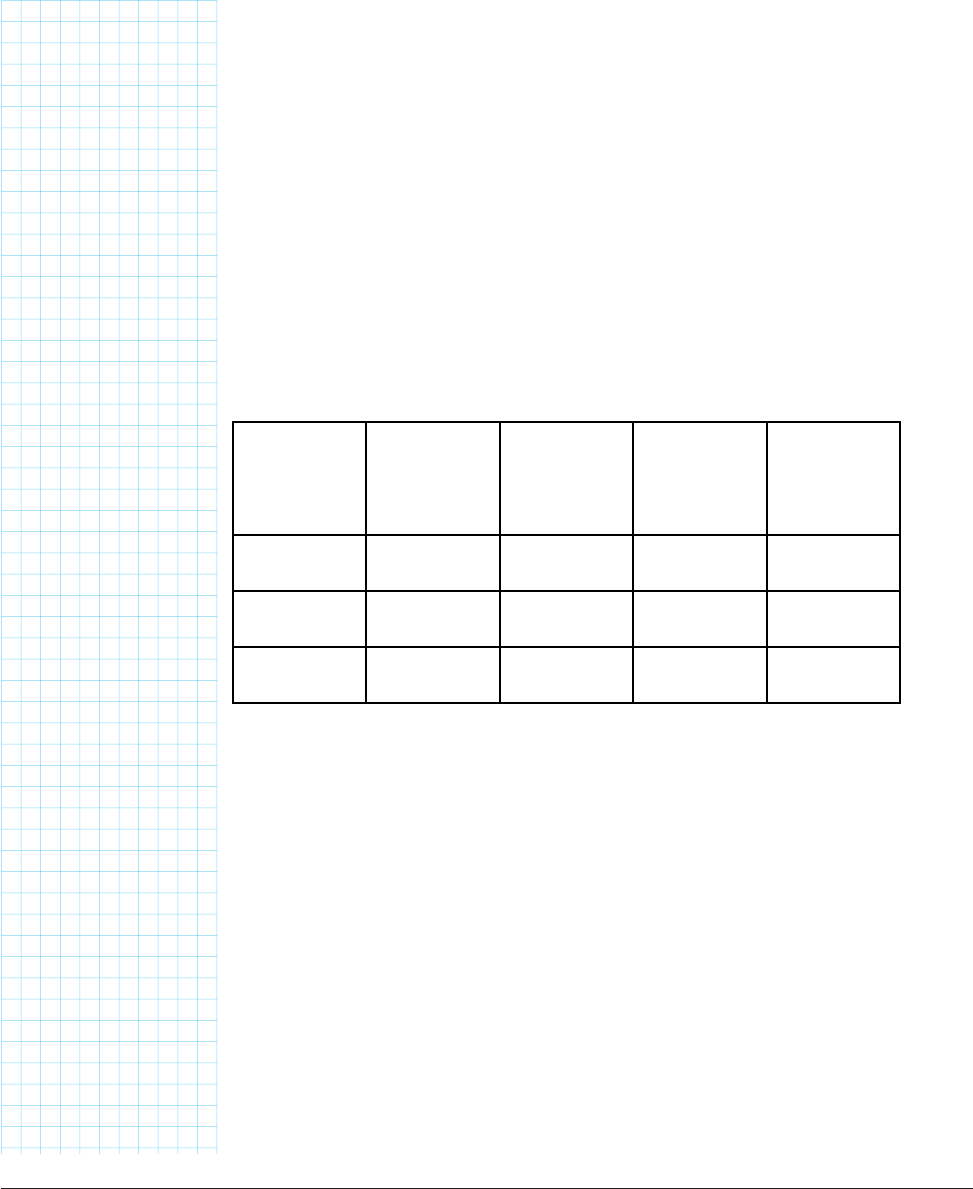
Try filling out the rest of this table with what the sign of sine, cosine, and
tangent would be in each range of angles by looking back over this section.
(Answer at the end of the chapter.)
0° to 90° 90° to 180° 180° to 270° 270° to 0°
(or -90° to
0°)
Sine +
Cosine +
Tangent +
ARCSIN, ARCCOS, ARCTAN
Suppose we wanted to “go backwards” and, given a sine, cosine, tangent or
other ratio, find out what angle corresponds to it. In the case of sine of an
angle A, this is called the arcsine (written asin( ), or sometimes arcsin( ) or
inverse sine (written sin
-1
() ). The other ratios have inverses named similarly.
For example sin(30°)= 0.5, so asin(0.5) = 30°; cos(60°) = 0.5, so acos(0.5) = 60°
and tan(26.6°) = 0.5, so atan(0.5) = 26.6°.
You might realize from the previous section that there are infinitely many
angles that have the same values of sine, cosine, etc. since these functions
repeat themselves (the official term is that they are periodic). Calculators will
return the principal value of angles. For arcsine and arctangent, this ranges
from -90° to 90°. For arccosine, the range is 0° to 180°. That way, there is no
ambiguity about what the calculator is returning. Check the physical situation
or any drawing you have to see if this is right. Also, be sure you know whether
Make: Geometry 119
118 Chapter 6: Pythagoras and a Little Trigonometry
Geometry_Chapter10_v15.indd 118Geometry_Chapter10_v15.indd 118 6/23/2021 9:09:52 AM6/23/2021 9:09:52 AM
you are working in degrees or radians.
A good way to be sure you’re doing something right is to take the sine of an
angle, get the answer, and use a calculator to take the asin() of that answer.
We did that a couple of paragraphs back when we showed how to go back
and forth between sin(30°) and asin(0.5). Note that on some calculators, you
need to hit another button (sort of like a shift key) to get to these functions.
SUMMARY AND LEARNING MORE
The Pythagorean Theorem is one of the best-known pieces of mathemat-
ics, and a little searching will give you more proofs if you would like to see it
approached differently. To follow up on the trigonometry introduction, check
out the Trigonometric Functions entry in Wikipedia. For more on sine (note
that cosine and tangent only have links that redirect to the Trigonometric
Functions Wikipedia entry) see the Sine entry. The Khan Academy has many
videos in this space as well.
In the next chapter, you also are going to learn about circles. You will do that
in part by trying out constructions, creating geometrical relationships with
just a compass and straightedge. You’ll also have enough pieces after that to
use the ideas in this book so far to figure out your latitude just by observing
shadows around lunchtime.
Make: Geometry 119
Geometry_Chapter10_v15.indd 119Geometry_Chapter10_v15.indd 119 6/23/2021 9:09:53 AM6/23/2021 9:09:53 AM

ANSWERS
Here are the answers for the activities in this chapter that we don’t solve in the text of the section.
HYPOTENUSE MODEL
• Use the model to find what angle will give you a sine of about 0.71.
• Answer: 45°
• What is the cosine of this angle?
• Answer: also 45°- if one angle of a right triangle is 45° the other one has to be, too.
• Describe what happens to the sine, cosine, and tangent of an angle when the angle gets close
to zero.
• Answer: sine approaches zero, too (as the opposite side shrinks). Cosine approaches 1
as the adjacent side becomes about the same as the hypotenuse. Tangent approaches
zero, since it is sine divided by cosine.
• What about as it gets close to 90°?
• Answer: sine approaches 1 (as the opposite side and hypotenuse approach being equal
lengths to each other.). Cosine approaches 0 as the adjacent side vanishes. Tangent
approaches infinity, since it is sine divided by cosine.
CALCULATING WITH SINE AND COSINE
• I have an angle of 45° in a triangle with a hypotenuse 5cm long. Length of the opposite side =
sin(45°) * 5cm = 0.7071 * 5cm = 3.54cm
• What is the length of the adjacent side? Also 3.54cm.
• Check to see that you are right by using the Pythagorean Theorem.
• 3.54
2
+ 3.54
2
= 25 = 5
2
and so it works.
ANGLES GREATER THAN 90°
0° to 90° 90° to 180° 180° to 270° 270° to 0°
(or -90° to 0°)
Sine + + - -
Cosine + - - +
Tangent + - + -
Make: Geometry 121
120 Chapter 6: Pythagoras and a Little Trigonometry
Geometry_Chapter10_v15.indd 120Geometry_Chapter10_v15.indd 120 6/23/2021 9:09:53 AM6/23/2021 9:09:53 AM

Make: Geometry 121
Geometry_Chapter10_v15.indd 121Geometry_Chapter10_v15.indd 121 6/23/2021 9:09:53 AM6/23/2021 9:09:53 AM
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
